Similar presentations:
8_Кодирование_состояний_автомата_для_минимизации_комбинационной
1. Кодирование состояний автомата для минимизации комбинационной схемы
2. Кодирование состояний автомата для минимизации комбинационной схемы
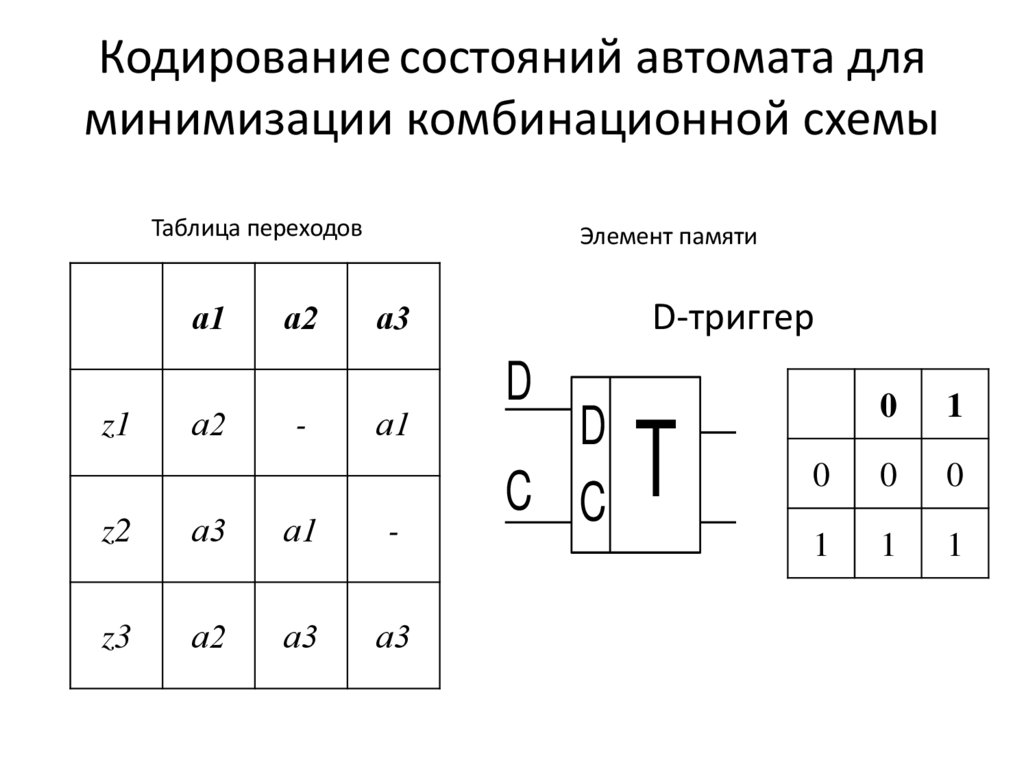
Таблица переходова1
z1
а2
а2
-
Элемент памяти
а3
а1
z2
а3
а1
-
z3
а2
а3
а3
D-триггер
D
D
C C
T
0
1
0
0
0
1
1
1
3. Кодирование состояний автомата для минимизации комбинационной схемы
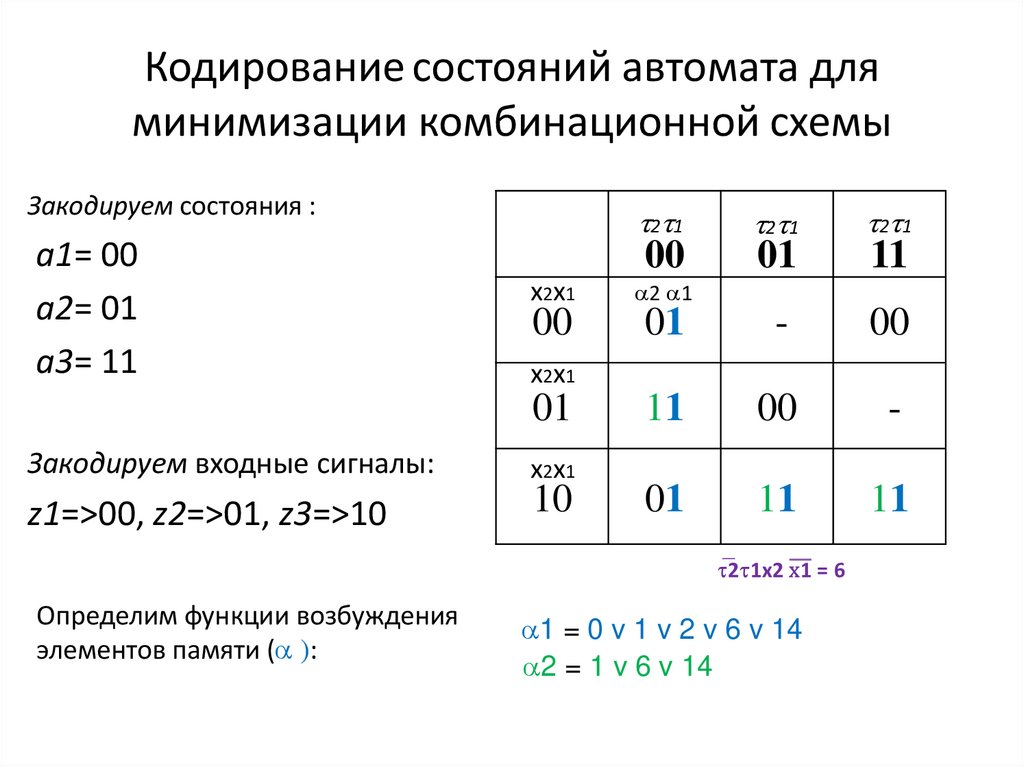
Закодируем состояния :а1= 00
а2= 01
а3= 11
х2х1
00
2 1
2 1
00
01
11
01
-
00
11
00
-
01
11
11
2 1
х2х1
01
Закодируем входные сигналы:
2 1
х2х1
z1=>00, z2=>01, z3=>10
10
Определим функции возбуждения
элементов памяти ( ):
1 = 0 v 1 v 2 v 6 v 14
2 = 1 v 6 v 14
4. Кодирование состояний автомата для минимизации комбинационной схемы
2 101
х2х1
2 1
00
10
Закодируем состояния по-другому:
10
00
-
01
2 a1 => 01
2 a2 => 10
3 a3 => 00
01
00
01
-
10
10
00
00
1 0 9
2 4 6
1 0 1 2 6 14
2 1 6 14
5. Кодирование состояний автомата для D-триггера
1. Каждому состоянию ставится в соответствие целоечисло Nm, равное числу переходов в состояние аm.
2. Числа Nm сортируются по убыванию.
3. Состояние с наибольшим N кодируются 00…00.
4. Следующие I состояний (I-число ЭП) кодируются
00..01, 00..10 … 10..00
5. Для кодирования оставшихся состояний
используются коды, содержащие 2, затем 3
единицы и т.д., пока все состояния не будут
закодированы.
6.
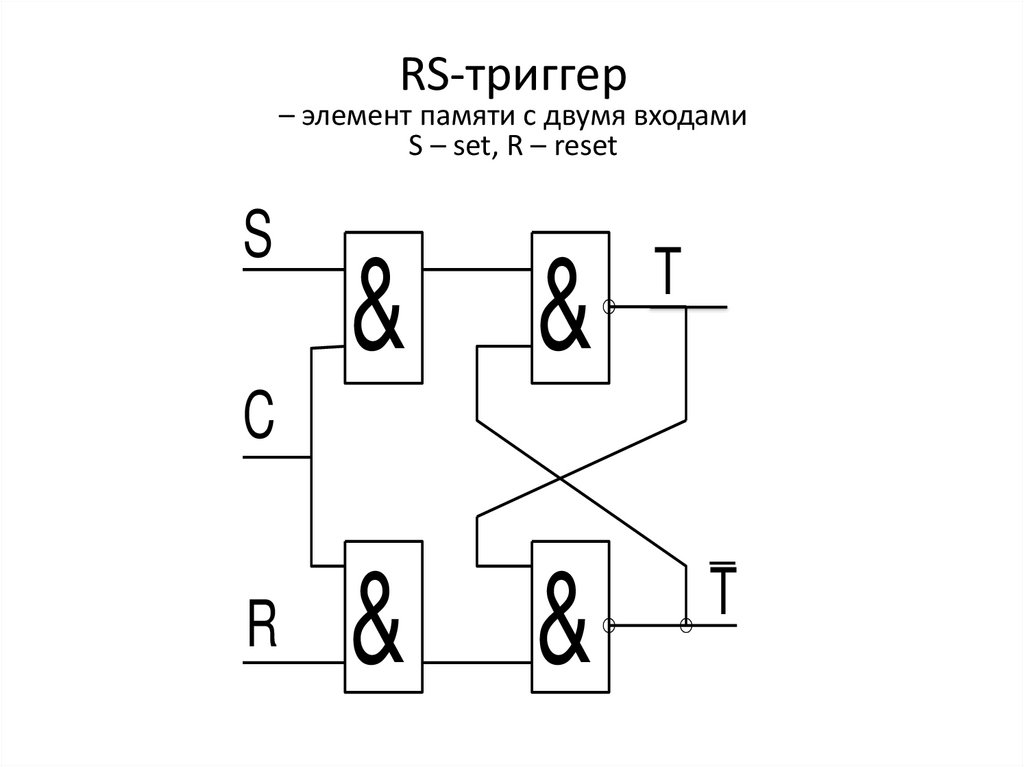
RS-триггер– элемент памяти с двумя входами
S – set, R – reset
S
& &
T
C
R
& &
T
7.
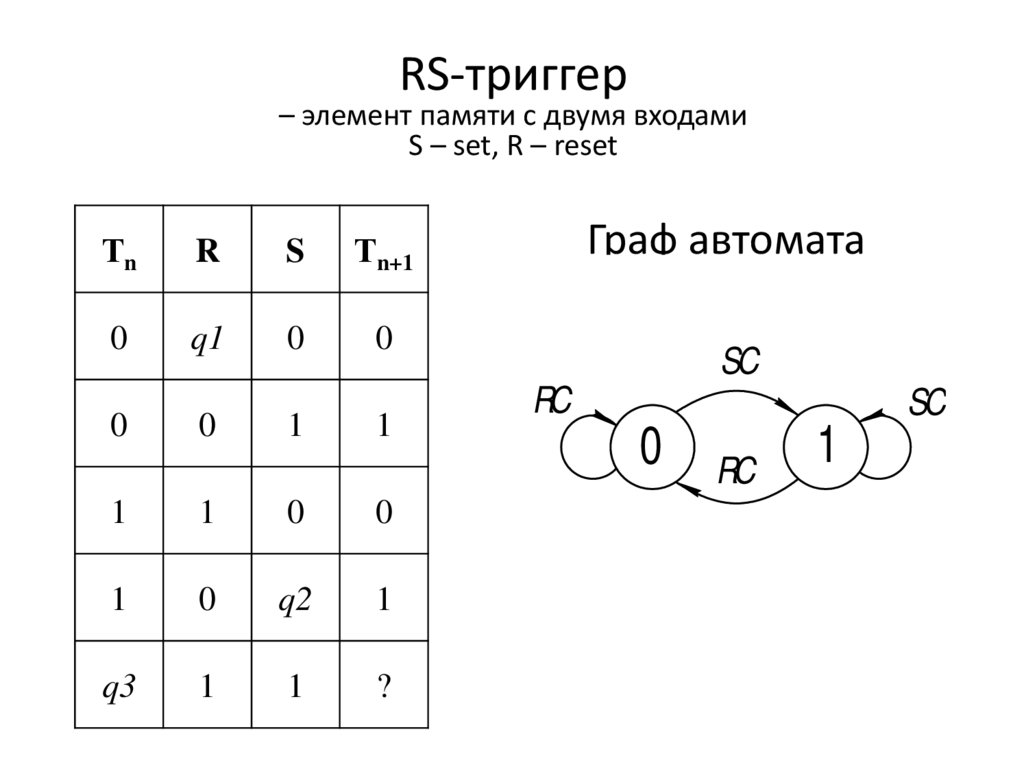
RS-триггер– элемент памяти с двумя входами
S – set, R – reset
Тn
R
S
Тn+1
0
q1
0
0
0
0
1
1
1
1
0
0
1
0
q2
1
q3
1
1
?
Граф автомата
SC
RC
SC
0
RC
1
8.
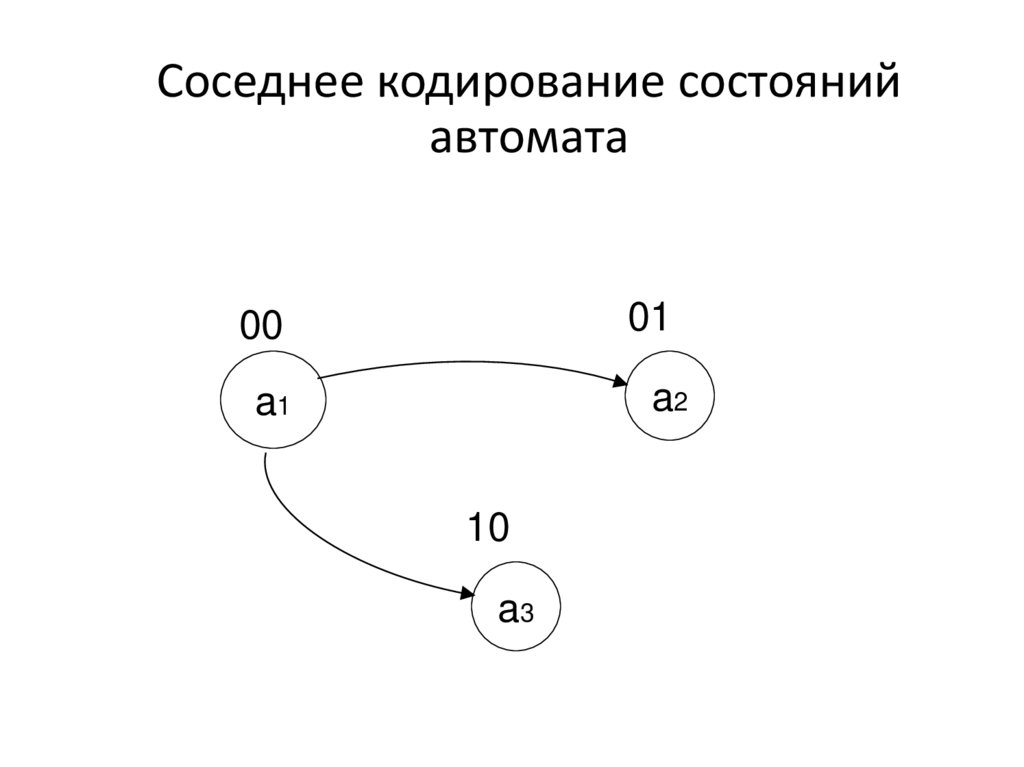
Соседнее кодирование состоянийавтомата
00
01
a1
a2
10
a3
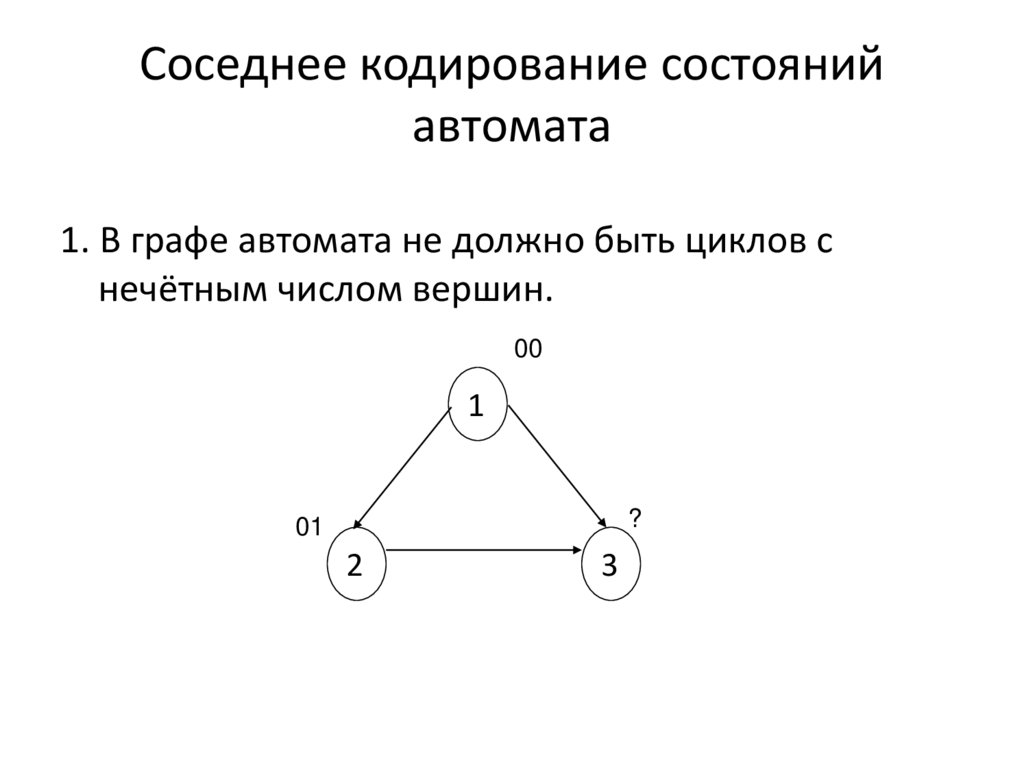
9. Соседнее кодирование состояний автомата
1. В графе автомата не должно быть циклов снечётным числом вершин.
00
1
?
01
2
3
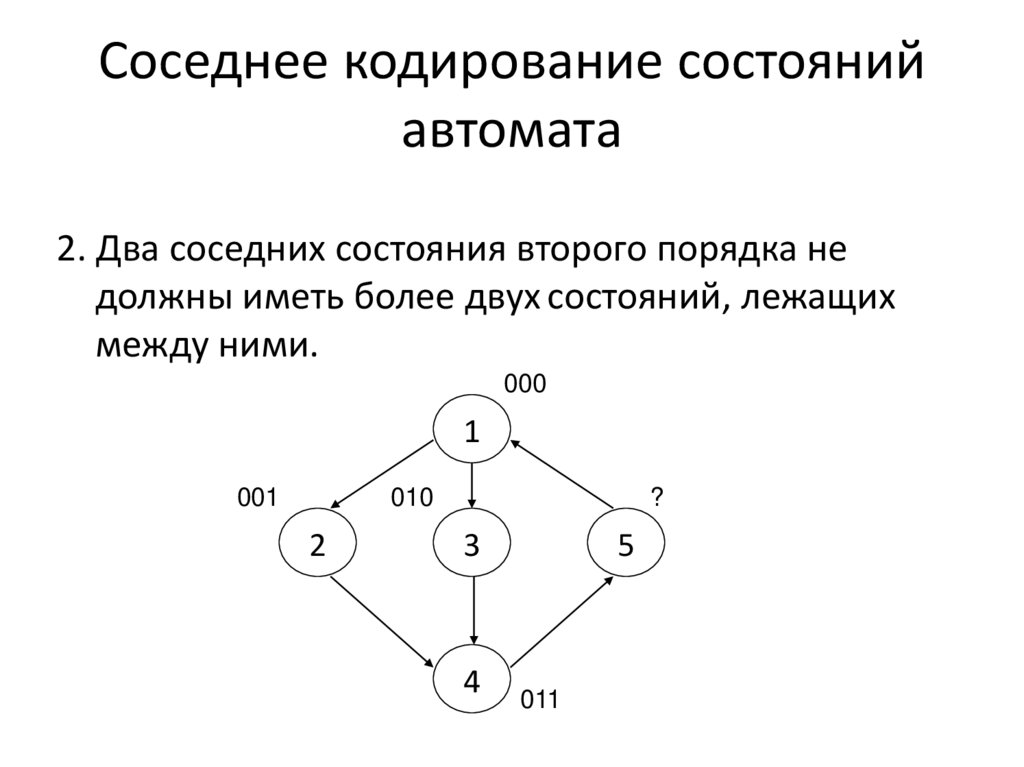
10. Соседнее кодирование состояний автомата
2. Два соседних состояния второго порядка недолжны иметь более двух состояний, лежащих
между ними.
000
1
001
010
2
?
3
4
5
011
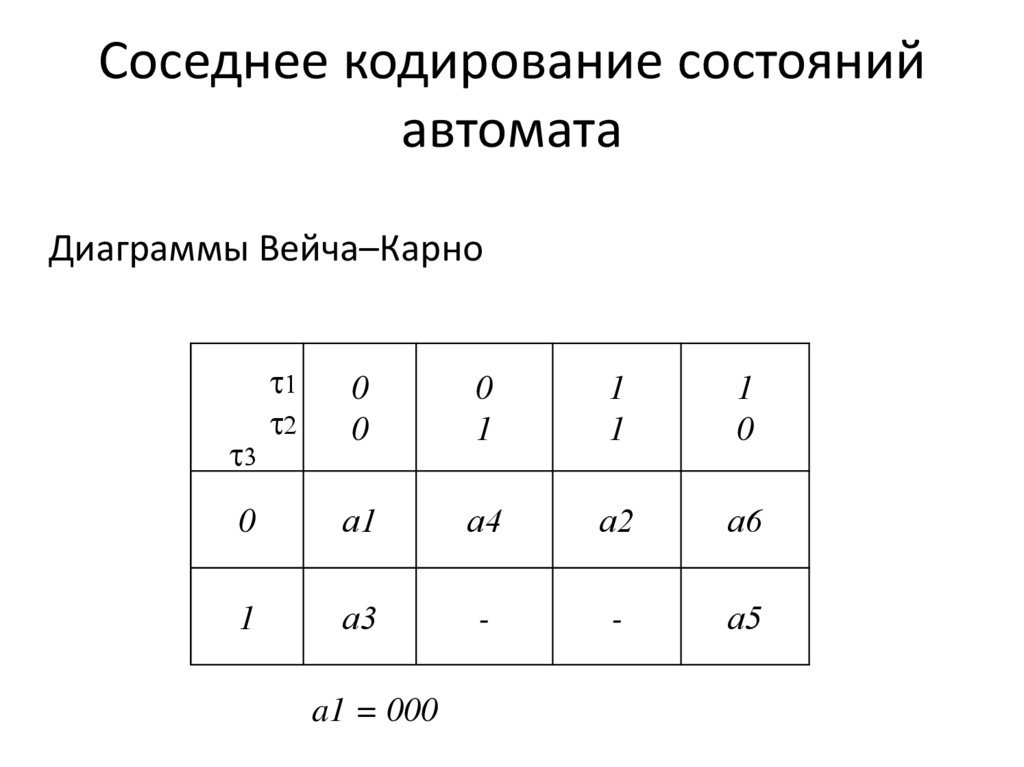
11. Соседнее кодирование состояний автомата
Диаграммы Вейча–Карно1
2
0
0
0
1
1
1
1
0
0
а1
а4
а2
а6
1
а3
-
-
а5
3
a1 = 000
12. Кодирование состояний автомата для RS, T, JK -триггеров
1. Строим матрицу, состоящую из различных пар номеров таких,a k a k
что в автомате S есть переход
1 1
M
k k
2а. Отсортируем строки матрицы М в соответствии с количеством связей у пары
состояний в строке (суммарно). Сортировка «по убыванию».
2. Переставим строки матрицы так, чтобы выполнялось условие:
( i i ) (( 1 1),..., ( i 1 i 1)) 0
Такую матрицу можно построить только для связного графа.
3. Закодируем состояния первой строки: k 1 00...00
k 1 00...01
4. Вычёркиваем из матрицы М первую строку. Получим матрицу М’.
13. Кодирование состояний автомата для RS, T, JK -триггеров
5. В начальной (верхней) строке матрицы М’ один элемент уже закодирован.6. Выберем незакодированный элемент первой строки матрицы
и обозначим его .
Построим матрицу М, выбрав из М’ все строки содержащие элемент .
7. Пусть множество B { 1 ,..., f ,..., F } - множество всех элементов матрицы М,
которые уже закодированы.
Для каждого кода k f найдём - множество кодов C 1 f , соседних с кодом
k f и ещё не занятых для кодирования состояний автомата. Построим
множество всех возможных кодов, соседних и еще незакодированных:
F
D C 1 f
1
1
Если нет ни одного множества с незакодированными элементами, то
количество ЭП выбрано неправильно.
14. Кодирование состояний автомата для RS, T, JK -триггеров
8. НаходимWgf k g k f
2
- кодовое расстояние для пар переходов
(«сколько триггеров переключается»)
9. Находим сумму всех кодовых расстояний
F
Wg Wgf
1
10. Выбираем код для состояния , у которого сумма кодовых расстояний
Wg - минимальна.
11. Из матрицы М’ вычеркиваем строки, в которых оба элемента закодированы,
получаем матрицу М”.
Если матрица М’ - пустая, переходим к пункту 12, иначе к пункту 5.
12. Вычисляем W t ms , сумму всех кодовых расстояний .
Оценкой качества кодирования рассмотренного алгоритма
может служить число К, где р - число переходов данного автомата.
K
W
p
Чем меньше К, тем ближе полученное кодирование к соседнему.
Эксперименты показали, что К при хорошем кодировании лежит
в пределах 1,4 K 2,1