Similar presentations:
Параллельность прямых и плоскостей. Параллельные прямые в пространстве. Параллельность трех прямых
1.
Глава I. Параллельностьпрямых и плоскостей.
Параллельные прямые в
пространстве.
Параллельность трех прямых.
1
2.
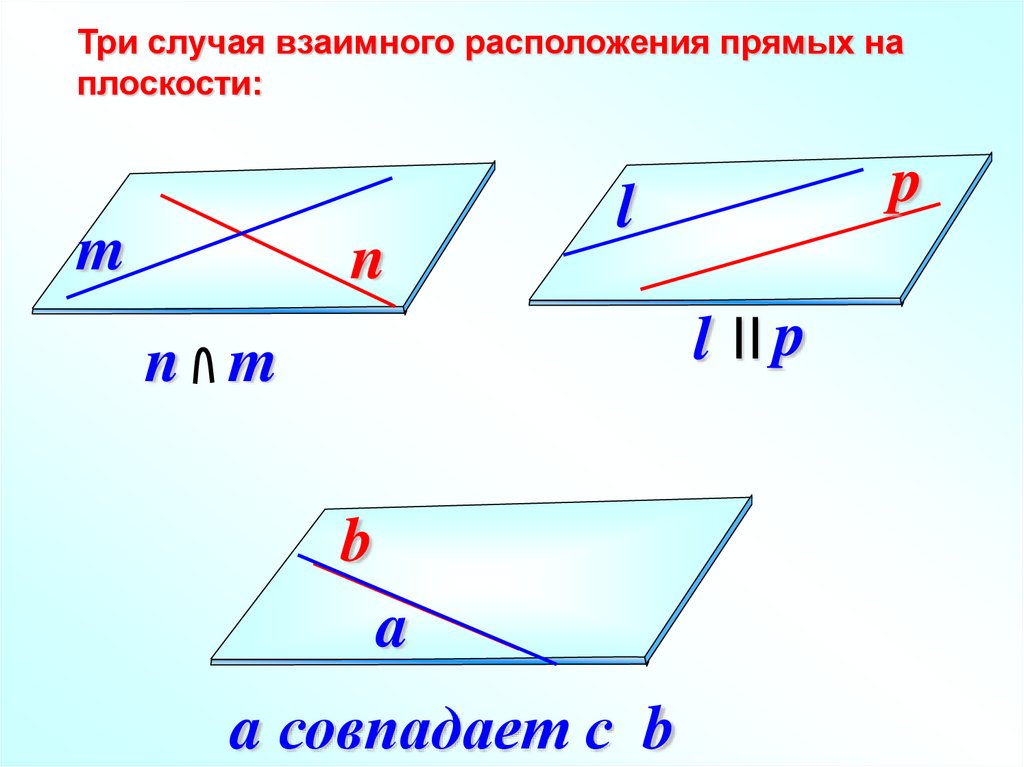
Три случая взаимного расположения прямых наплоскости:
m
n
p
l
l II p
n m
b
a
a совпадает с b
3.
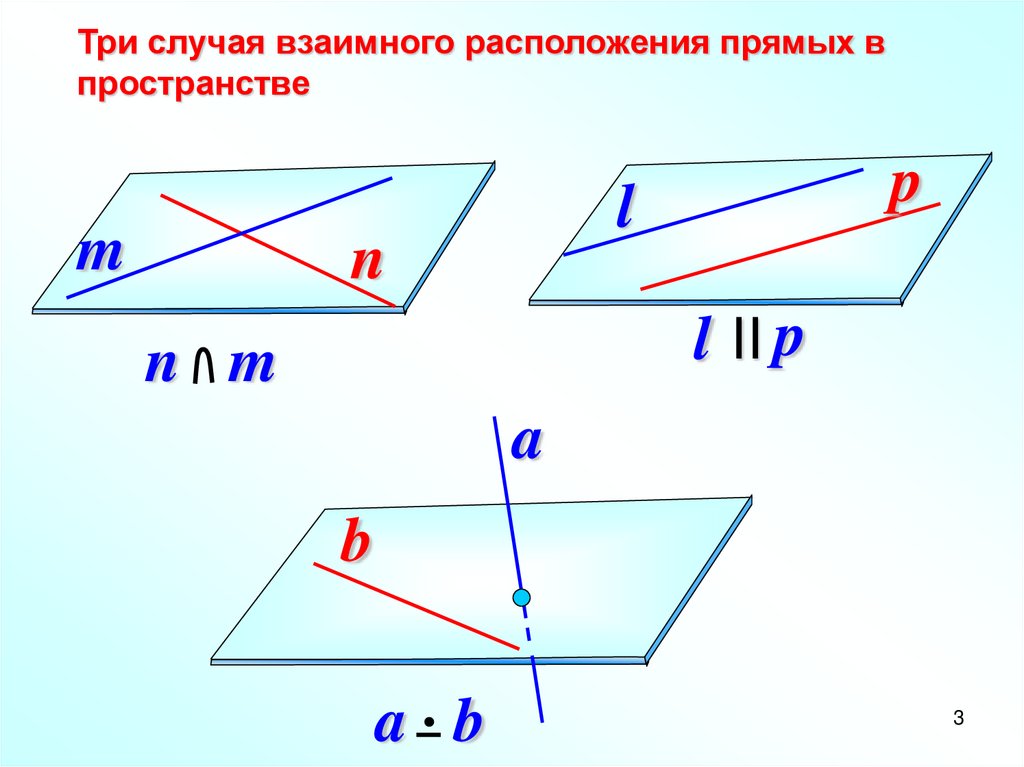
Три случая взаимного расположения прямых впространстве
m
p
l
n
l II p
n m
a
b
a b
3
4.
ПланиметрияСтереометрия
Две прямые на
плоскости называются
параллельными, если
они не пересекаются.
Две прямые в
пространстве
называются
параллельными, если
они лежат в одной
плоскости и не
пересекаются.
aIIb
aIIb
4
5.
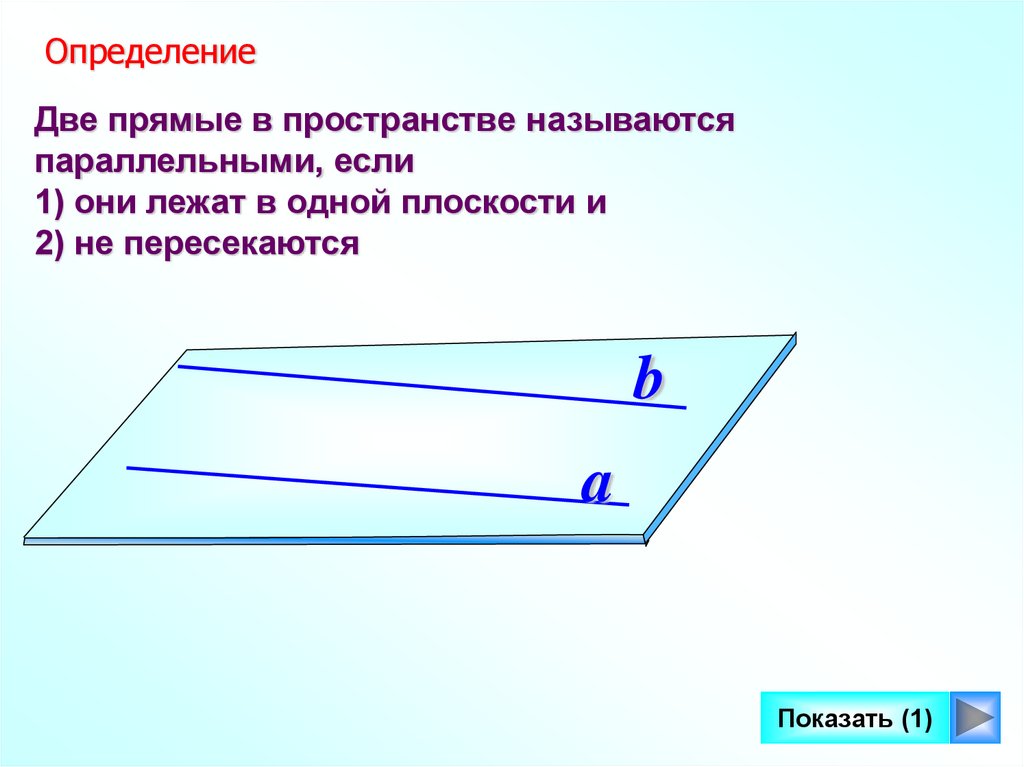
ОпределениеДве прямые в пространстве называются
параллельными, если
1) они лежат в одной плоскости и
2) не пересекаются
b
a
Показать (1)
5
6.
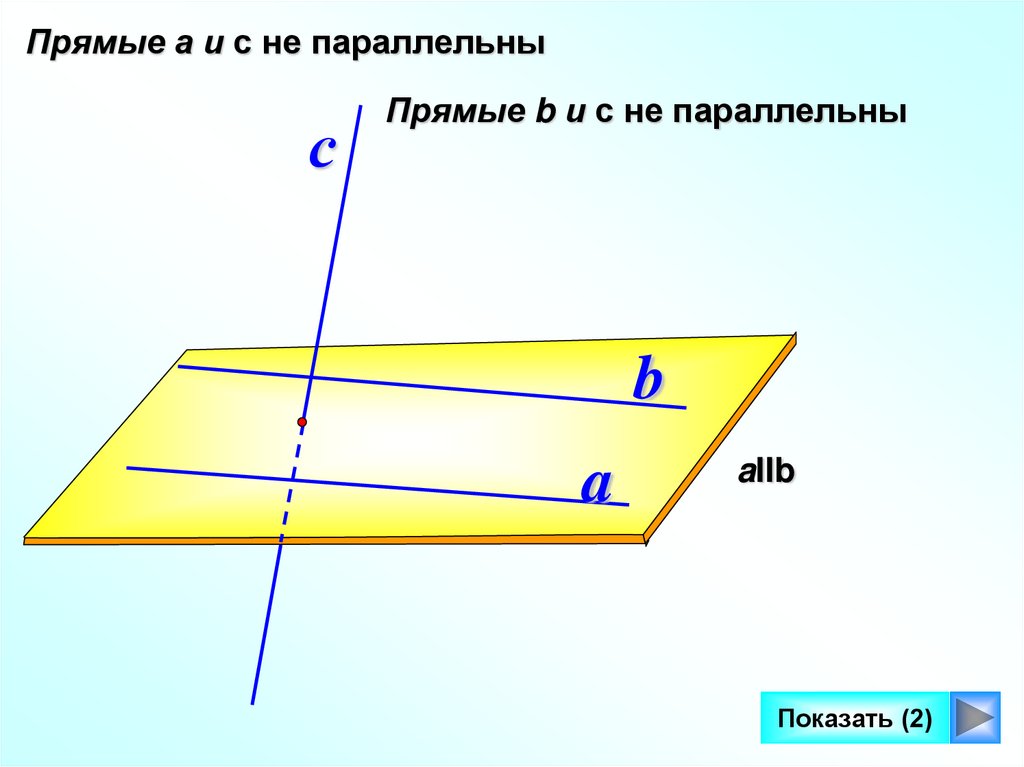
Прямые а и с не параллельныс
Прямые b и с не параллельны
b
a
aIIb
Показать (2)
6
7.
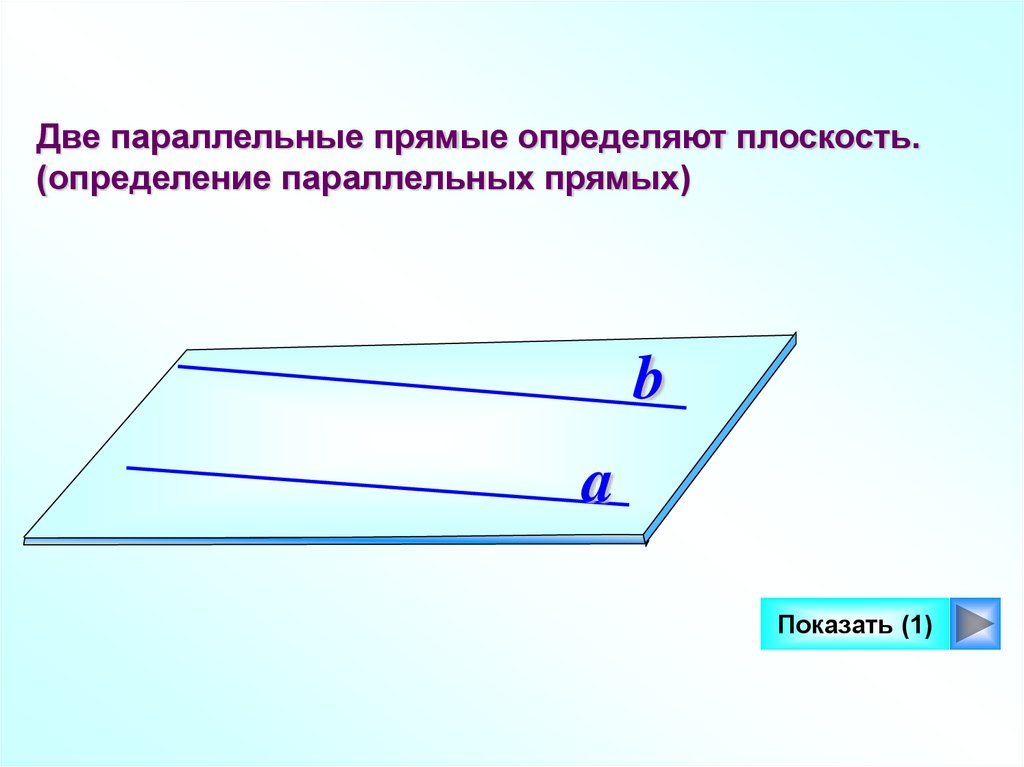
Две параллельные прямые определяют плоскость.(определение параллельных прямых)
b
a
Показать (1)
7
8.
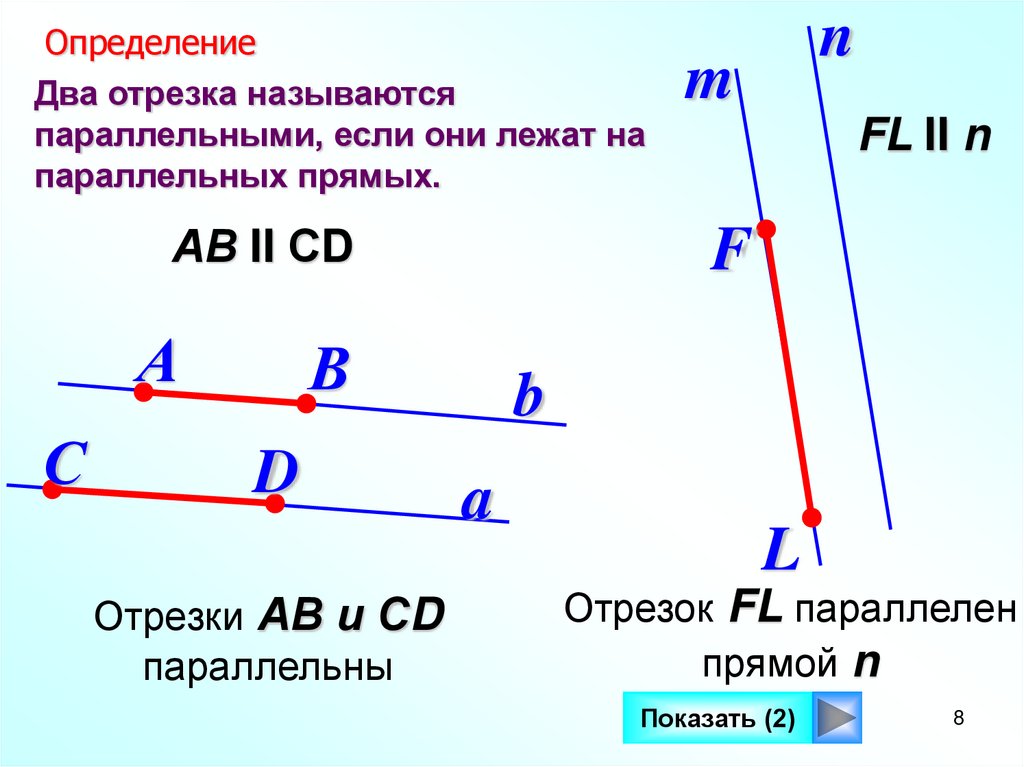
ОпределениеДва отрезка называются
параллельными, если они лежат на
параллельных прямых.
АВ II СD
А
С
Отрезки АВ и СD
параллельны
m
FL II n
F
В
D
n
b
a
L
Отрезок FL параллелен
прямой n
Показать (2)
8
9.
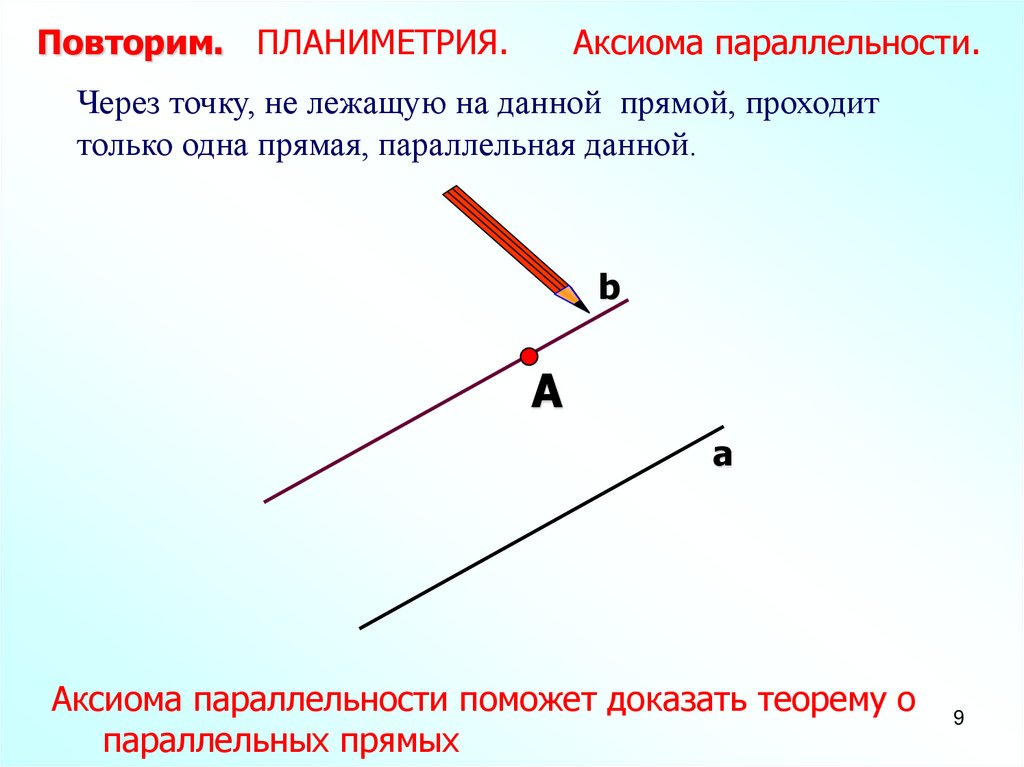
Повторим. ПЛАНИМЕТРИЯ.Аксиома параллельности.
Через точку, не лежащую на данной прямой, проходит
только одна прямая, параллельная данной.
b
А
а
Аксиома параллельности поможет доказать теорему о
параллельных прямых
9
10.
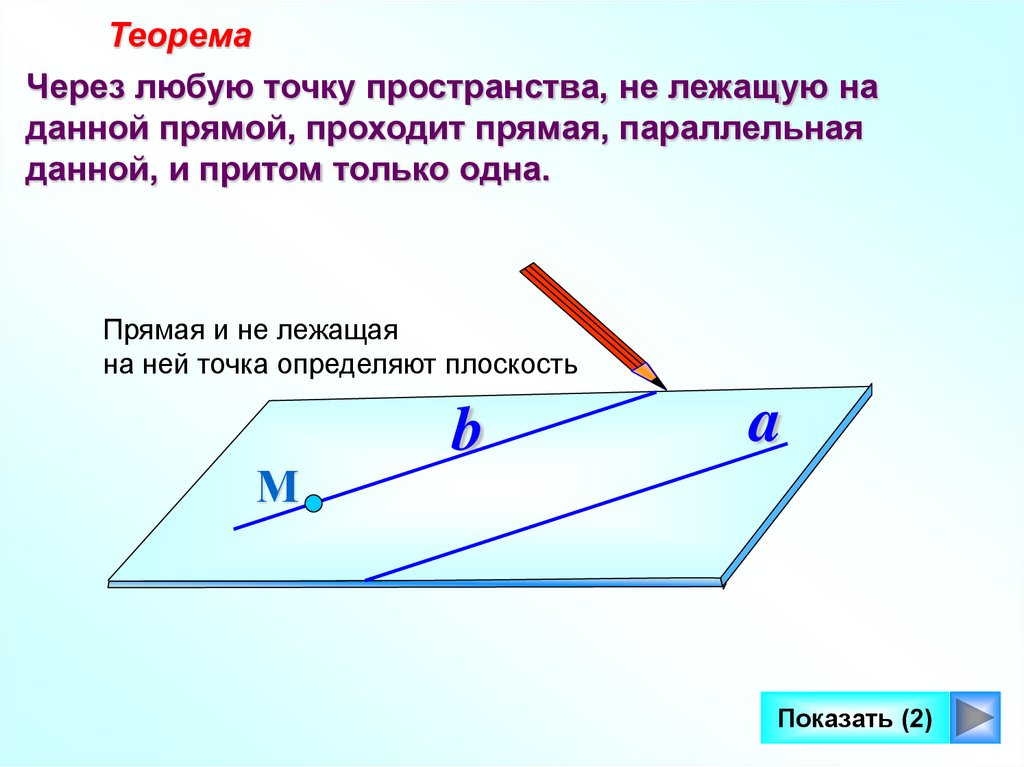
ТеоремаЧерез любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная
данной, и притом только одна.
Прямая и не лежащая
на ней точка определяют плоскость
М
b
a
Показать (2) 10
11.
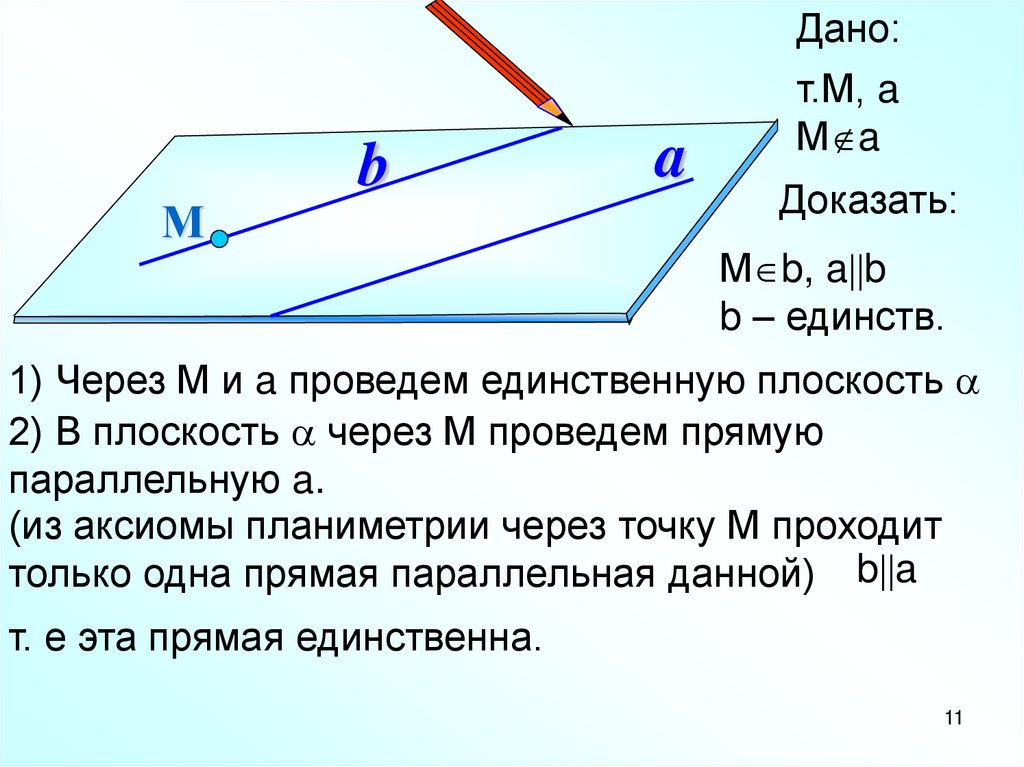
Дано:М
b
a
т.М, a
М a
Доказать:
М b, a b
b – единств.
1) Через М и a проведем единственную плоскость
2) В плоскость через М проведем прямую
параллельную a.
(из аксиомы планиметрии через точку М проходит
только одна прямая параллельная данной) b a
т. е эта прямая единственна.
11
12.
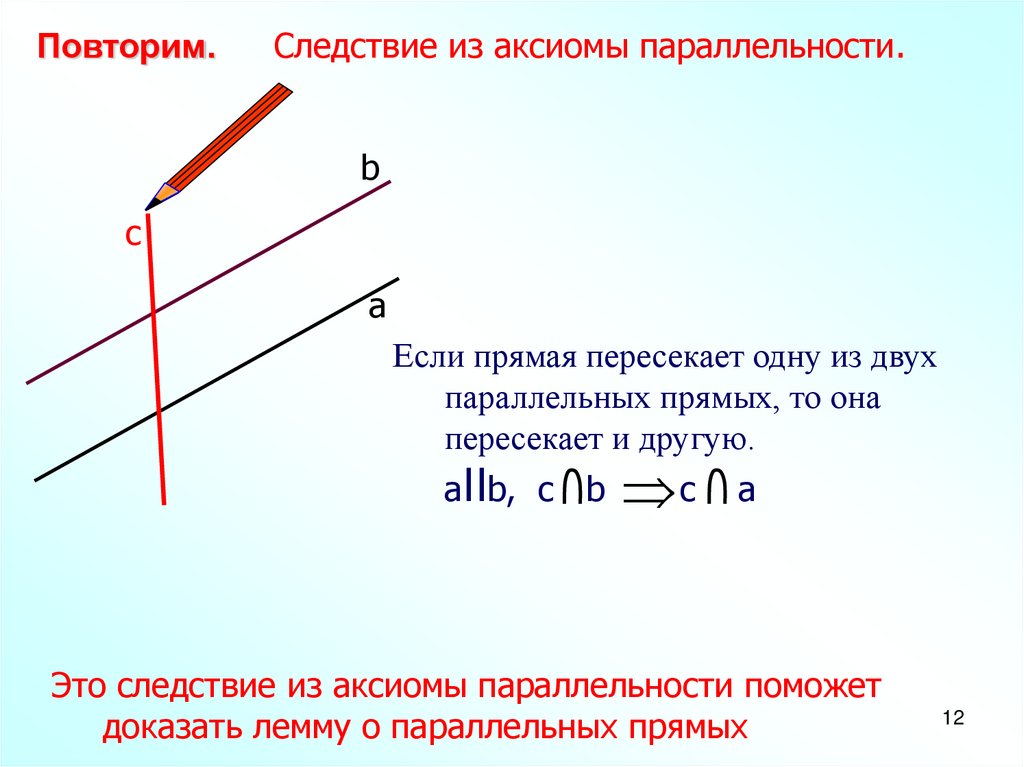
Повторим.Следствие из аксиомы параллельности.
b
c
а
Если прямая пересекает одну из двух
параллельных прямых, то она
пересекает и другую.
aIIb, c b
c
a
Это следствие из аксиомы параллельности поможет
доказать лемму о параллельных прямых
12
13.
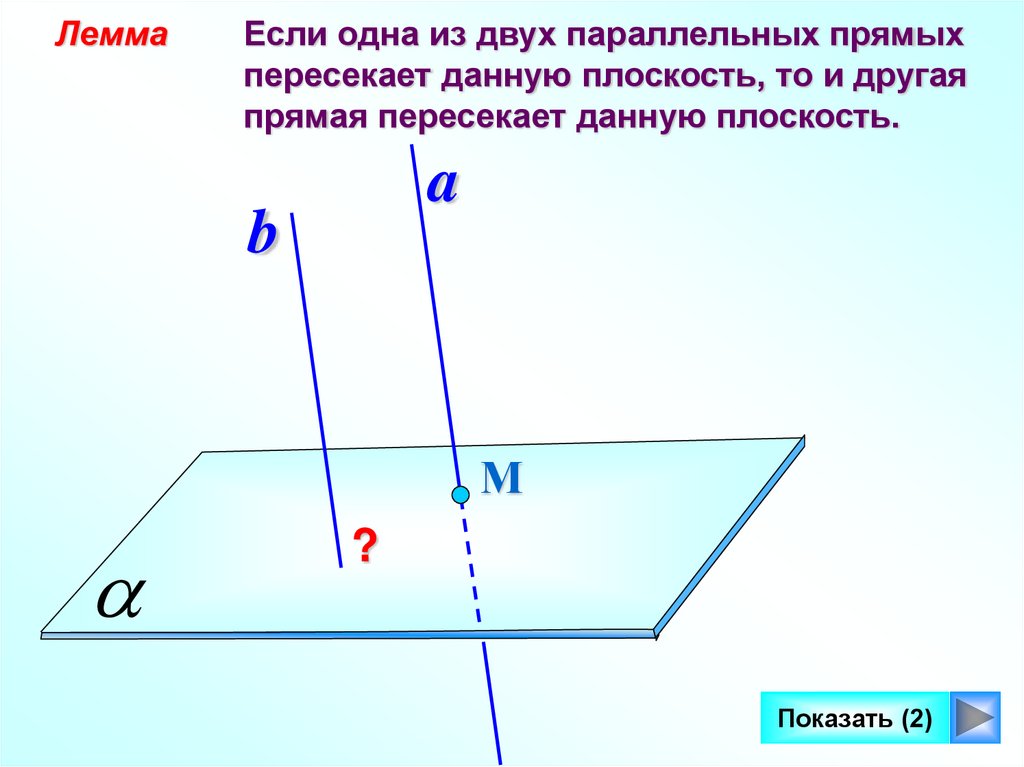
ЛеммаЕсли одна из двух параллельных прямых
пересекает данную плоскость, то и другая
прямая пересекает данную плоскость.
a
b
М
?
Показать (2) 13
14.
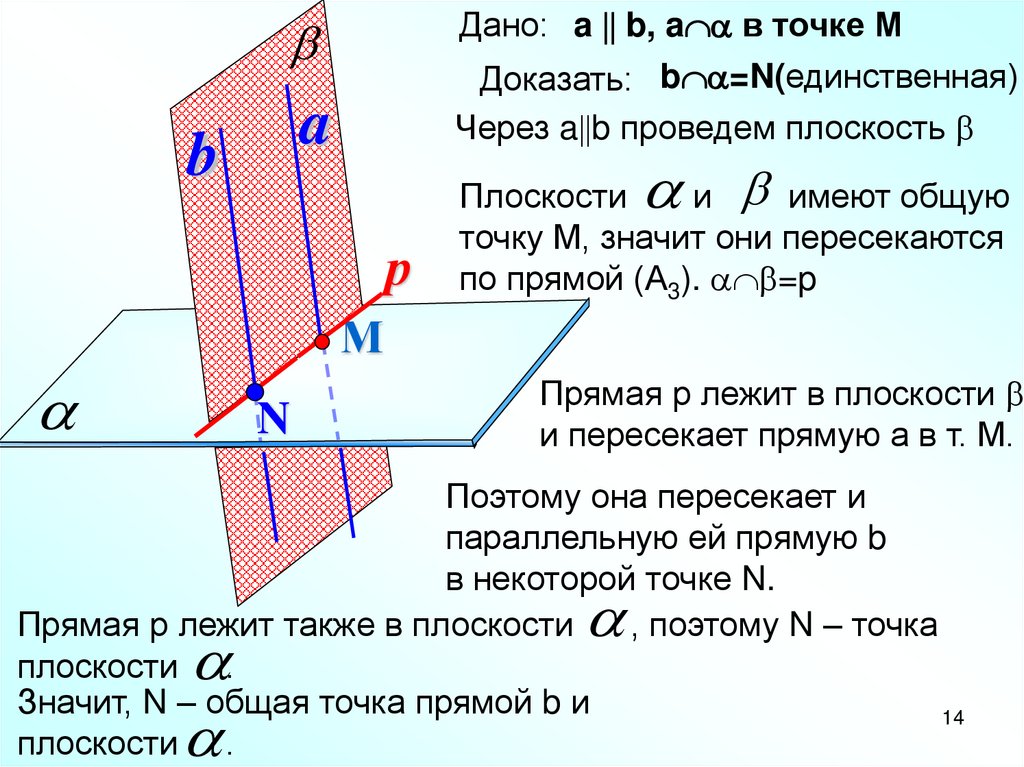
Дано: a b, a в точке МДоказать: b =N(единственная)
Через a b проведем плоскость
a
b
р
Плоскости
и имеют общую
точку М, значит они пересекаются
по прямой (А3). =p
М
N
Прямая р лежит в плоскости
и пересекает прямую а в т. М.
Поэтому она пересекает и
параллельную ей прямую b
в некоторой точке N.
Прямая р лежит также в плоскости
, поэтому N – точка
плоскости .
Значит, N – общая точка прямой b и
14
плоскости .
15.
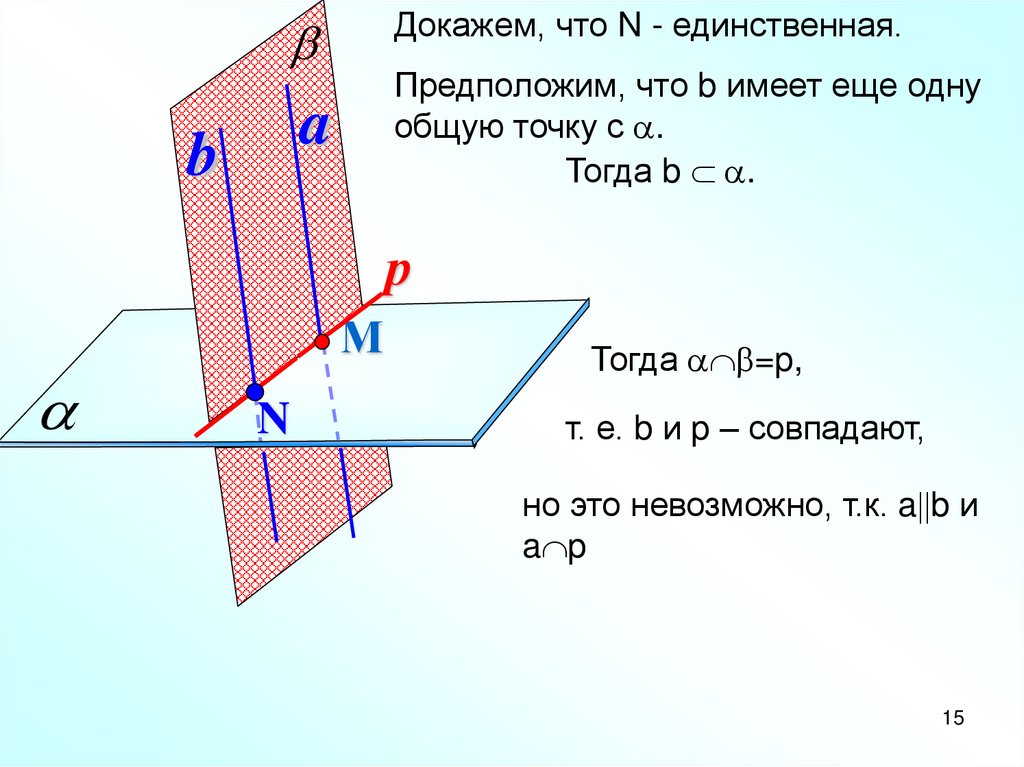
Докажем, что N - единственная.Предположим, что b имеет еще одну
общую точку с .
Тогда b .
a
b
р
М
N
Тогда =p,
т. е. b и p – совпадают,
но это невозможно, т.к. a b и
a p
15
16.
Теоремас
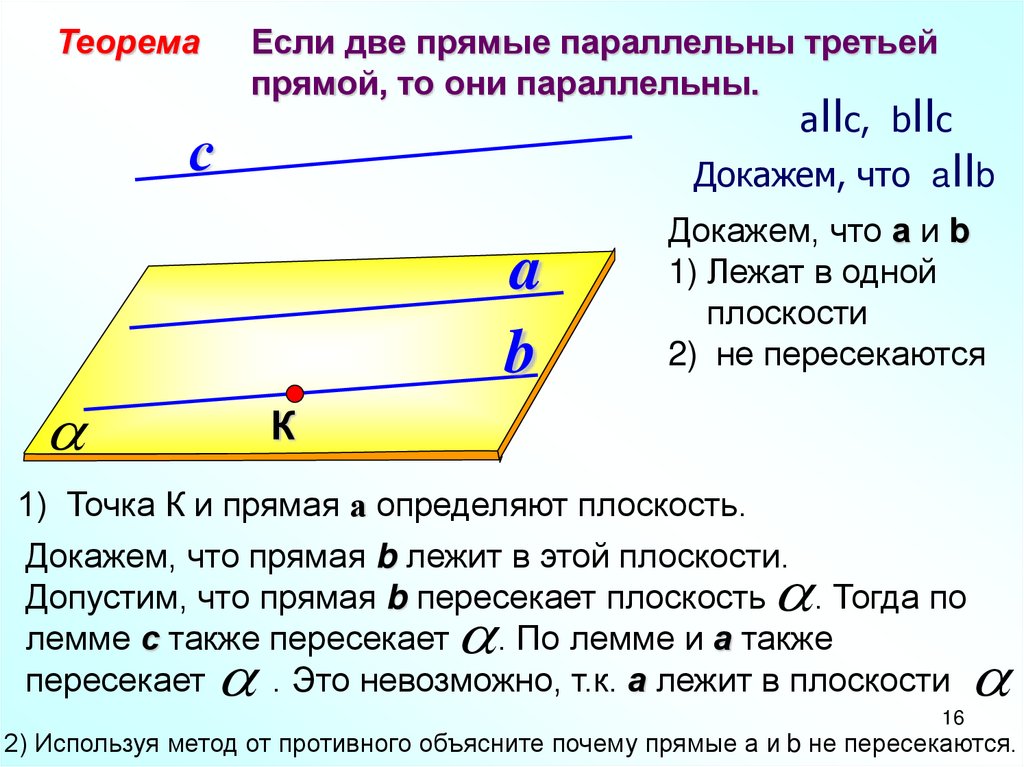
Если две прямые параллельны третьей
прямой, то они параллельны.
aIIс, bIIс
Докажем, что aIIb
a
b
Докажем, что а и b
1) Лежат в одной
плоскости
2) не пересекаются
К
1) Точка К и прямая а определяют плоскость.
Докажем, что прямая b лежит в этой плоскости.
Допустим, что прямая b пересекает плоскость . Тогда по
лемме с также пересекает . По лемме и а также
пересекает
. Это невозможно, т.к. а лежит в плоскости
16
2) Используя метод от противного объясните почему прямые а и b не пересекаются.
17.
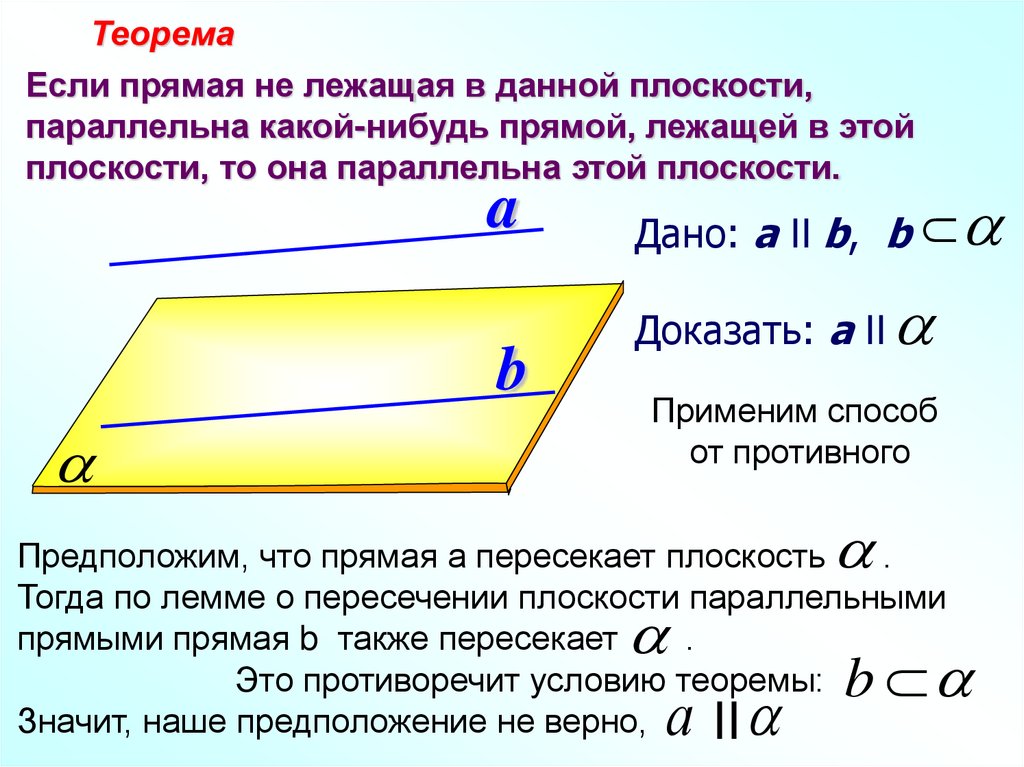
ТеоремаЕсли прямая не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна этой плоскости.
a
b
Дано: a II b, b
Доказать: a II
Применим способ
от противного
Предположим, что прямая а пересекает плоскость
.
Тогда по лемме о пересечении плоскости параллельными
прямыми прямая b также пересекает
.
Это противоречит условию теоремы:
Значит, наше предположение не верно,
II
а
b


 mathematics
mathematics








