Операции над событиями. Урок №3

1.

Урок №3 на тему
«Операции над событиями»

2.

Теория вероятностей –
раздел математики,
изучающий случайные
явления.

3.

Случайное событие
это
явление,
происходит
в
которое
результате
осуществления
какого-либо
определенного
комплекса
условий.

4.

Случайное опыт
(случайный эксперимент)
это
условия
и
обстоятельства, в которых
мы
рассматриваем
случайные события.

5.

Невозможное
случайное
случайное
событие,
событие
которое
в
–
это
случайном
эксперименте не наступает.
Достоверное
случайное
случайное
событие,
событие
которое
в
эксперименте обязательно наступит.
–
это
случайном

6.

События
разделить
случайного
на
более
опыта,
которые
простые,
нельзя
называются
элементарными событиями или элементарными
исходами.

7.

Как обозначается вероятность?
Вероятности событий мы будем
обозначать буквой P латинского
алфавита,
по
начальной
букве
латинского слова «probabilitas»,
что и значит «вероятность».

8.

Свойства вероятностей
элементарных событий:
1) Вероятности элементарных
событий неотрицательны.
2) Сумма вероятностей всех
элементарных
равняется единице.
событий

9.

Элементарные
события
называются
равновозможными, если все они имеют
одинаковые шансы на осуществление.

10.

Если
в
случайном
опыте
ровно
N
равновозможных элементарных событий, то
вероятность каждого из них равна

11.

Правило.
В
элементарными
равна
опыте
с
событиями
отношению
благоприятствующих
числа
равновозможными
вероятность события А
элементарных
событию
А,
к
событий,
общему
числу
элементарных событий.
Р(А) - вероятность события А,
N - общее количество элементарных событий,
N(A)
-
количество
элементарных
благоприятствующих событию А.
событий,

12.

Случайный выбор – это разновидность
случайного
опыта
с
равновозможными
элементарными событиями.

13.

Случайный выбор или выбор наудачу
означает выбор без каких-либо
предпочтений.
Выбор наудачу входит как часть во
многие игры: наудачу выбирают
номер при игре в лото; наудачу
выбирают карты во многих
карточных играх; в лотереях
наудачу выбирают номера
выигрышных билетов и т.п.

14.

Событие
, противоположное
событию А, — это событие, которое
состоит из всех элементарных
событий случайного опыта, не
благоприятствующих событию А.

15.

Взаимно противоположные
события
Сумма
вероятностей
всех
элементарных событий случайного
опыта равна 1.

16.

Достоверное и невозможное события
взаимно противоположны.

17.

Диаграммы Эйлера (круги Эйлера)
Первое
их
использование
приписывают Леонарду Эйлеру
–
великому
швейцарского
который
провёл
в
математику
происхождения,
почти
полжизни
России,
где
внёс
вклад
в
существенный
становление российской науки.

18.

Диаграммы Эйлера
(круги Эйлера)
это
наглядная схема, с помощью
которой можно изобразить отношения
между событиями в одном эксперименте,
для наглядного представления.

19.

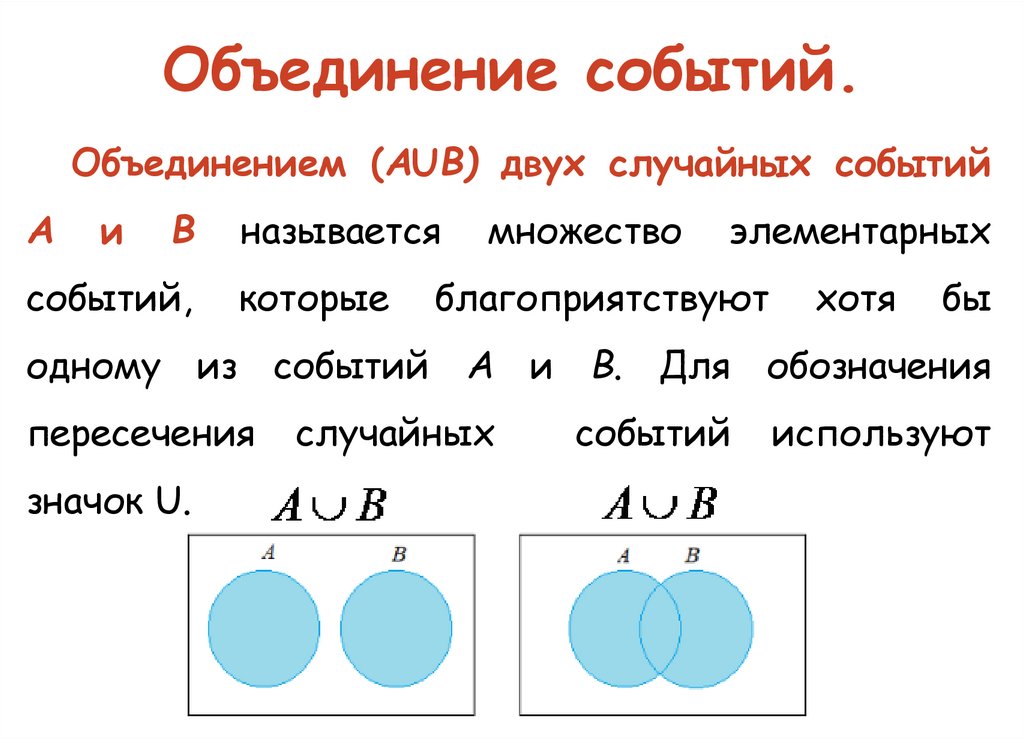
Объединение событий.
Объединением (АUВ) двух случайных событий
А
и
В
событий,
называется
которые
множество
элементарных
благоприятствуют
хотя
бы
одному из событий А и В. Для обозначения
пересечения
значок U.
случайных
событий
используют

20.

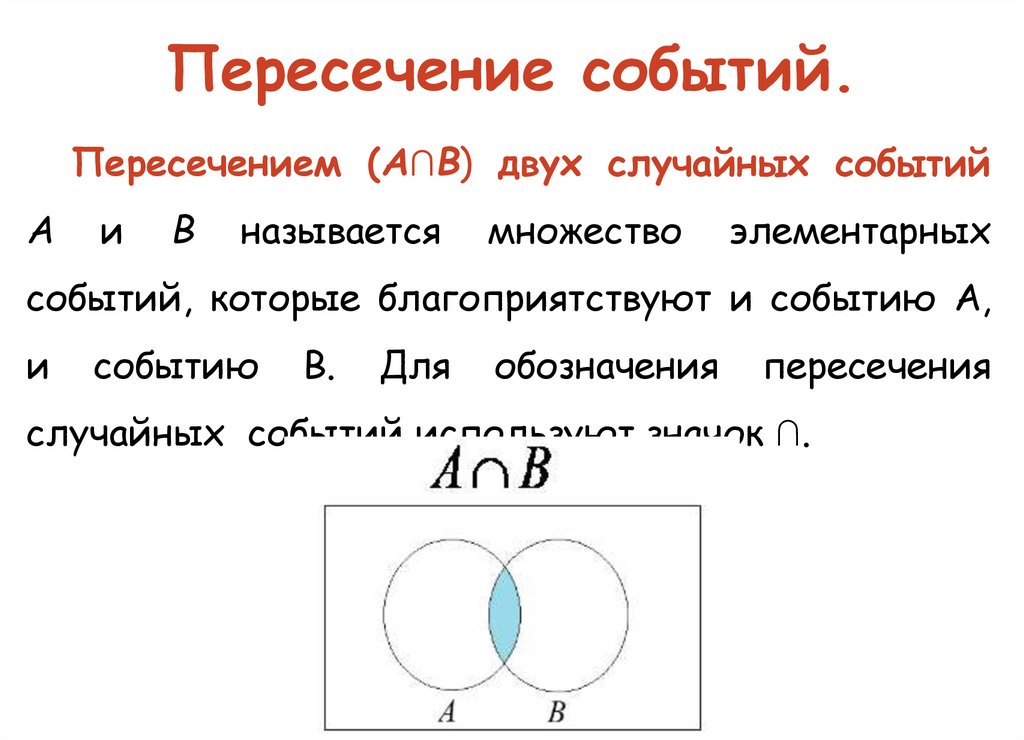
Пересечение событий.
Пересечением (А∩В) двух случайных событий
А
и
В
называется
множество
элементарных
событий, которые благоприятствуют и событию А,
и
событию
В.
Для
обозначения
пересечения
случайных событий используют значок ∩.

21.

Пустое событие
Пусто событие – это событие, которое не
содержит элементарных исходов.
Пустое событие обозначают символом Ø.
Можно написать: А∩В=Ø.

22.

Правило сложения вероятностей
несовместных событий
Вероятность
несовместных
объединения
событий
сумме их вероятностей:
равна

23.

Совместные события
Если
B
могут
одновременно
наступить
в
результате
опыта,
события
события
одного
A
называются
событиями.
и
то
эти
совместными

24.

Формула сложения
вероятностей
Формула
сложения
вероятностей.
Вероятность
объединения двух событий равна
сумме
их
вероятностей
вероятности их пересечения:
без

25.

Условная вероятность
Вероятность события А при условии,
что событие В произошло, называется
условной вероятностью события А при
условии события В.
Обозначается эта вероятность: P(А/В).

26.

Правило умножения
вероятностей
Вероятность пересечения двух событий
равна
произведению
вероятности
одного из них на условную вероятность
другого, вычисленную при условии,
что первое имело место.