Лекция Метод Байеса

1. Машинное обучение и нейросетевые технологии

2.

Кол-во
Кол-во
аудиторных часов лекционных часов
92
50
Кол-во часов
практических
занятий
42
Формы
промежуточной
аттестации
Контрольная,
экзамен

3. Основные методы

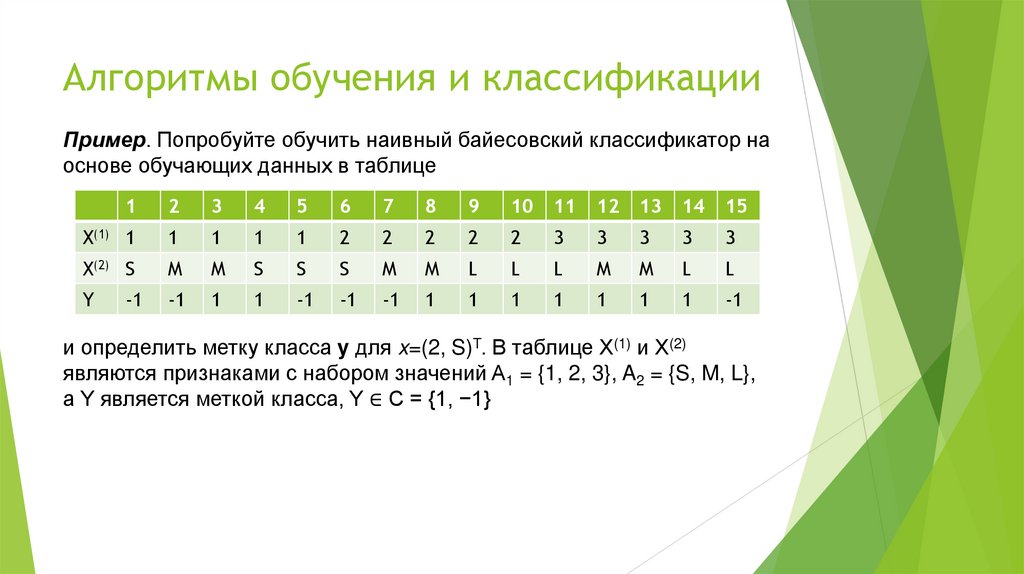
Пусть входное пространство X ⊆ Rn будет набором n-мерных векторов, а
выходное пространство будет множеством меток классов Y={c1,c2,...,cK}.
Входные данные — вектор признаков x ∈ X , а выходные данные — метка
класса y ∈ Y. X — случайный вектор, определенный на входном пространстве
X , а Y — случайная величина, определенная на выходном пространстве Y.
P(X, Y) — совместное распределение вероятностей X и Y. Обучающий
набор данных T = {(x1, y1), (x2, y2), . . . , (xN,yN)} генерируется P(X, Y),
независимыми одинаково распределенными.
Наивный Байес изучает совместное распределение вероятностей P(X, Y)
из обучающего набора данных. А именно, изучаются следующие априорное
распределение вероятностей и условное распределение вероятностей.
Априорное распределение вероятностей равно
P(Y=ck), k=1,2,…,K.
Распределение условной вероятности

4. Основные методы

Рассмотрим совместное распределение вероятностей P(X, Y).
Условное распределение вероятностей P(X = x|Y = ck) имеет
экспоненциальное число параметров, поэтому его оценка практически
неосуществима. Фактически, предположим, что x(j) имеет Sj
возможных значений, j = 1, 2, . . . , n, а Y имеет K возможных значений,
тогда число параметров равно