Матан

1. Функции и их графики.

ФУНКЦИИ И ИХ
ГРАФИКИ.
Свойства и графики
основных элементарных
функций.

2. Словарь:

СЛОВАРЬ:
Функция(социол.) – роль,
которую
выполняет определенный социальный
институт или процесс.
Функция государства, семьи в жизни
общества.
Функция – деятельность, обязанность,
работа.
Функция денег...
functio
(лат.) - исполнение,
осуществление.
o Функция(матем.) – соответствие
величинами.
между

3. В МАТЕМАТИКЕ ПРИНЯТО ОБОЗНАЧЕНИЕ:

Читается:
функция эф от икс,
функция игрек от икс.

4. 1.Определение:

1.ОПРЕДЕЛЕНИЕ:
Функция - это зависимость
между двумя переменными
Х и У, при которой каждому
значению Х из области
определения
соответствует единственное
значение У.

5. 2. Способы задания функций:

2. СПОСОБЫ ЗАДАНИЯ
ФУНКЦИЙ:
1.Аналитический
(формула).
2.Табличный.
3.Графический.

6. 3.ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ:

D(y)- область определения
функции – это множество
значений Х, где функция
определена и выражена
действительным числом.

7. 4.ОБЛАСТЬ ЗНАЧЕНИЯ ФУНКЦИИ:

E(y)- область
значения функции –
это множество
значений у.

8. 5. Монотонность функции:

5. МОНОТОННОСТЬ
ФУНКЦИИ:
( интервалы возрастания и убывания).
а) Функция называется возрастающей,
если большему значению Х
соответствует большее значение У .
б) Функция называется убывающей,
если большему значению Х
соответствует меньшее значение У.

9. 6. ЧЕТНОСТЬ НЕЧЕТНОСТЬ ФУНКЦИИ:

.
6. ЧЕТНОСТЬ
НЕЧЕТНОСТЬ ФУНКЦИИ:
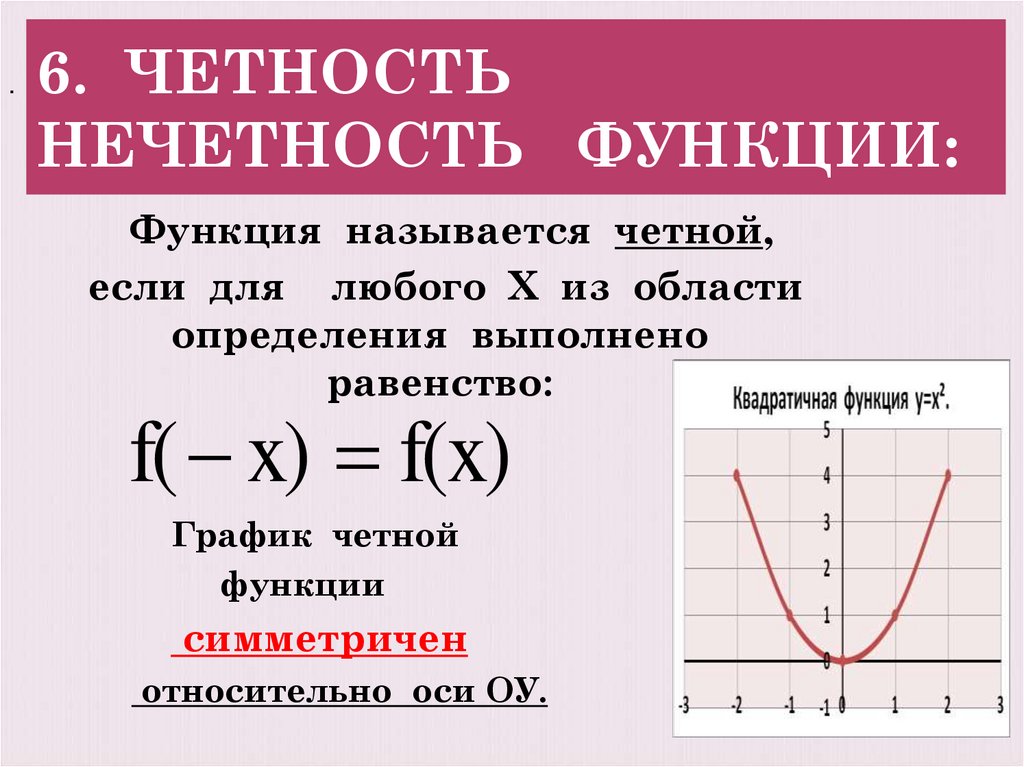
Функция называется четной,
если для любого Х из области
определения выполнено
равенство:
f( x) f(x)
График четной
функции
симметричен
относительно оси ОУ.

10. 6. ЧЕТНОСТЬ НЕЧЕТНОСТЬ ФУНКЦИИ:

.
6. ЧЕТНОСТЬ
НЕЧЕТНОСТЬ ФУНКЦИИ:
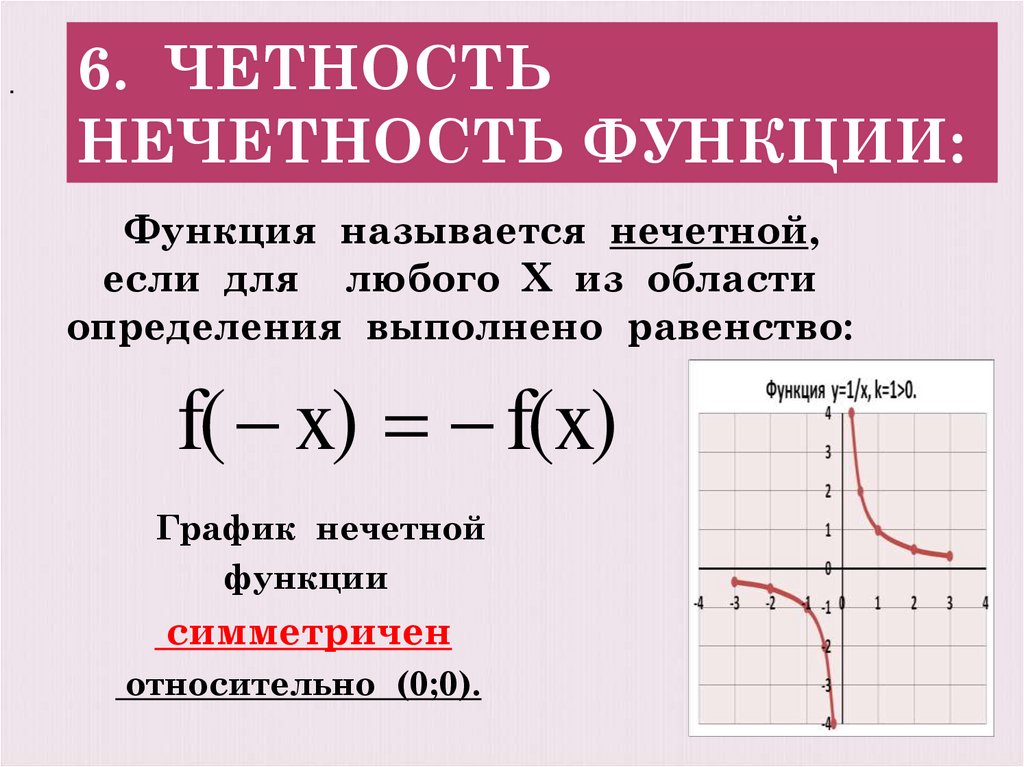
Функция называется нечетной,
если для любого Х из области
определения выполнено равенство:
f( x) f(x)
График нечетной
функции
симметричен
относительно (0;0).

11. 7. Точки экстремума функции:

.
7. ТОЧКИ ЭКСТРЕМУМА
ФУНКЦИИ:
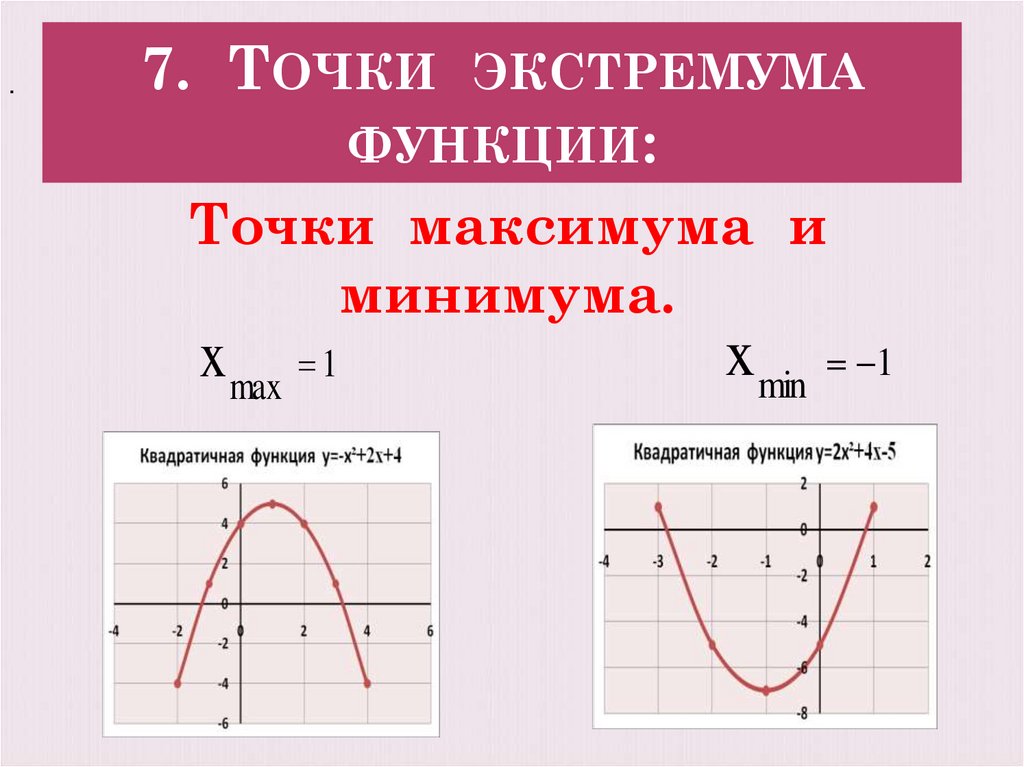
Точки максимума и
минимума.
x max 1
x min 1