14.51M

Category:

physics

ТЕМА 3. Закони Ньютона

1. Тема 3. Закони Ньютона.

2. Взаємодія

Причина зміни руху тіл — взаємодія між ними.
Завдяки взаємодії
тіла
набувають прискорення й зазнають деформації.

3. Сила

→
Сила F має величину й напрямок, тому це —
величина векторна.
Сила F— векторна величина, модуль якої є
мірою взаємодії тіл.
Одиниця вимірювання сили в СІ — Ньютон (Н).

4. Вимірювання сил

Один з приладів,
яким можна виміряти
модуль сили, —
динамометр.

5. Рівнодійна сил

→
→
→
→
Рівнодійна F сил F1, F2, F3, … — це сума
всіх сил, що діють на тіло:

6. Задача №1.

На повітряну кулю діють 3 сили:
сила тяжіння,
підйомна сила,
сила вітру.
Знайти рівнодійну силу.
Вважайте, що опором повітря
можна знехтувати.

7. Розв'язання

На повітряну кулю діють 3 сили:
→
сила тяжіння F1,
→
підйомна сила F2,
→
→
F2
сила вітру F3.
Усі сили діють в одній площині.
Центр тяжіння — в кошику.
Рівнодійна всіх сил:
→
F3
→
F1

8. Розв'язування

→
→
→
1. Оскільки F1 та F2 —
протилежні за напрямком
і лежать на одній прямій,
їх можна легко додати.
→
F1
→
F2
→
F1+F2
→
F3
→
F1

9. Розв'язування

2. Результат
додавання
→
→
F1 та F2 зображено на
рисунку.
→
→
F1+F2
→
F3

10. Розв'язування

3. Будуємо паралелограм
→ → →
із векторів F3, F1+F2.
→
→
F1+F2
→
F3

11. Розв'язування

4. Додавши їх за правилом
паралелограма, отримуємо
рівнодійну силу
→
→
→
→
F=F1+F2+F3.
→
→
→
F1+F2+F3
→
→
F1+F2
→
F3

12. Висновок

Як бачимо, напрямок
→
рівнодійної F всіх сил
відмінний від напрямку
будь якої із діючих сил.
→
F2
→
F
→
F3
→
F1

13. Перший закон Ньютона

Існують такі системи відліку,
які ми називаємо інерціальними.
В інерціальних системах відліку
тіла рухаються рівномірно і
прямолінійно або покояться,
якщо:
1. На них не діють жодні сили,
або
2. Рівнодійна всіх сил,
що діють на них, дорівнює нулю.
Приклад.
Салон автобуса.

14. Питання №2.

Система відліку, яка пов'язана з автобусом,
що починає рух, є інерціальною чи ні?

15. Міркування

Нехай система, пов'язана з
автобусом, є інерціальною.
Уявімо, що деяка людина
на зупинці спостерігає
за автобусом.
Спостерігач і автобус —
рівноправні.
Тоді можна вважати,
що в системі відліку водія саме спостерігач
прискоренно віддаляється від автобуса.

16. Міркування

З погляду водія, людина має
таке ж саме прискорення, що й автобус,
при тому, що рівнодійна сил,
які діють на людину, дорівнює нулю!
А в інерціальній системі відліку,
згідно її означення, спостерігач повинен рухатися
рівномірно-прямолінійно!
Маємо протиріччя!

17. Відповідь і висновки

Відповідь: ні!
Автобус, що прискорюється,
не є інерціальною системою відліку.
Отже, ті системи відліку,
що рухаються з прискоренням —
неінерціальні.
Характеристика інерціальних систем відліку:
вони або не рухаються,
або рухаються рівномірно і прямолінійно.

18. Питання № 2.

Тіло рухається рівномірно і прямолінійно.
Розгляньте наступні умови:
1. На тіло не діє жодна сила;
2. На тіло діє 1 сила;
3. На тіло діє одночасно 2 сили;
4. На тіло діє одночасно 3 сили.
Питання: За якої з цих умов такий рух
є принципово НЕможливим?

19. Інертність

Інертність — властивість тіла, яка характеризує
його здатність набувати прискорення під дією
певною сили.
Більш інертному тілу важче набути швидкість.

20. Маса

Маса m — міра інертності.
Маса має тільки величину, тому це —
величина скалярна.
Одиниця вимірювання маси в СІ — кілограм (кг).

21. Розрахунок маси

Для однорідних тіл
можна використати
формулу:
де ρ — густина,
при чому
а V — об'єм тіла (м3).
Пектораль з Товстої Могили —
приклад однорідного тіла
довільної форми.

22. Означення густини

Густина ρ — це маса речовини, яка
припадає на одиницю об'єму тіла.
Густина немає напрямку. Тому це —
величина скалярна.
Одиниця виміру густини в СІ —
кілограм на метр кубічний (
).

23. Другий закон Ньютона

В інерціальних системах відліку
→
прискорення тіла а прямо-пропорційне
→
рівнодійній усіх зовнішніх сил F й
обернено-пропорційне масі тіла m:

24. Другий закон Ньютона

ІІ закон Ньютона можна записати у формі:
→
де F — рівнодійна всіх діючих на тіло сил:
Ця форма зручна при розв'язуванні деяких задач.

25. Другий закон Ньютона

ІІ закон Ньютона у формі:
називають динамічним рівнянням руху.
Ця форма також зручна
при розв'язуванні деяких задач.

26. Другий закон Ньютона

ІІ закон Ньютона справедливий лише:
1. В інерціальних системах відліку;
2. Для тіл, які рухаються з невеликими,
порівняно зі швидкістю світла, швидкостями.

27. Другий закон Ньютона

ІІ закон Ньютона
не можна застосовувати
для опису руху елементарних частинок.

28. Вимірювання маси

В основі методів вимірювання
маси різних тіл покладений
II закон Ньютона.

29. Приклад №1.

Маса автомобіля 800 кг.
Рівняння його руху має вигляд:
.
Чому дорівнює модуль рівнодійної всіх
сил, що діють на автомобіль?

30. Задача

Дано:
m = 800 кг
F=?

31. Розв'язування

Щоб знайти модуль рівнодійної всіх сил,
можна скористатися другим законом Ньютона.
(1)
З умови задачі: m = 800 кг
а—?
Отже, треба знайти модуль прискорення а.

32. Розв'язування

Щоб знайти а, порівняймо відоме з умови
рівняння руху:
(2)
із тим, як воно виглядає в загальному випадку:
(3)
Із (2) і (3) отримуємо, що
Згідно з (1):

33. Питання №4.

Яка одна характеристика руху залишається
незмінною при переході з однієї до будь-якої
іншої інерціальної системи відліку?
а) переміщення;
б) швидкість;
в) прискорення.

34. Міркування.

Переміщення?
Це величина відносна.
Приклад:
Відносно трамваю пасажир нерухомий.
Відносно землі — він проходить кілометри.
Висновок: в різних інерціальних системах
переміщення теж різне.

35. Міркування

Швидкість?
Теж відносна величина.
Приклад:
Відносно пілота на відео
інші літаки наче нерухомі.
А відносно землі швидкість
більше 1000 км/год!
Висновок: в різних інерціальних системах
швидкість теж різна.

36. Відповідь.

Методом виключення доходимо висновку,
що саме прискорення зберігається
в різних інерціальних системах відліку.
Доведемо це!

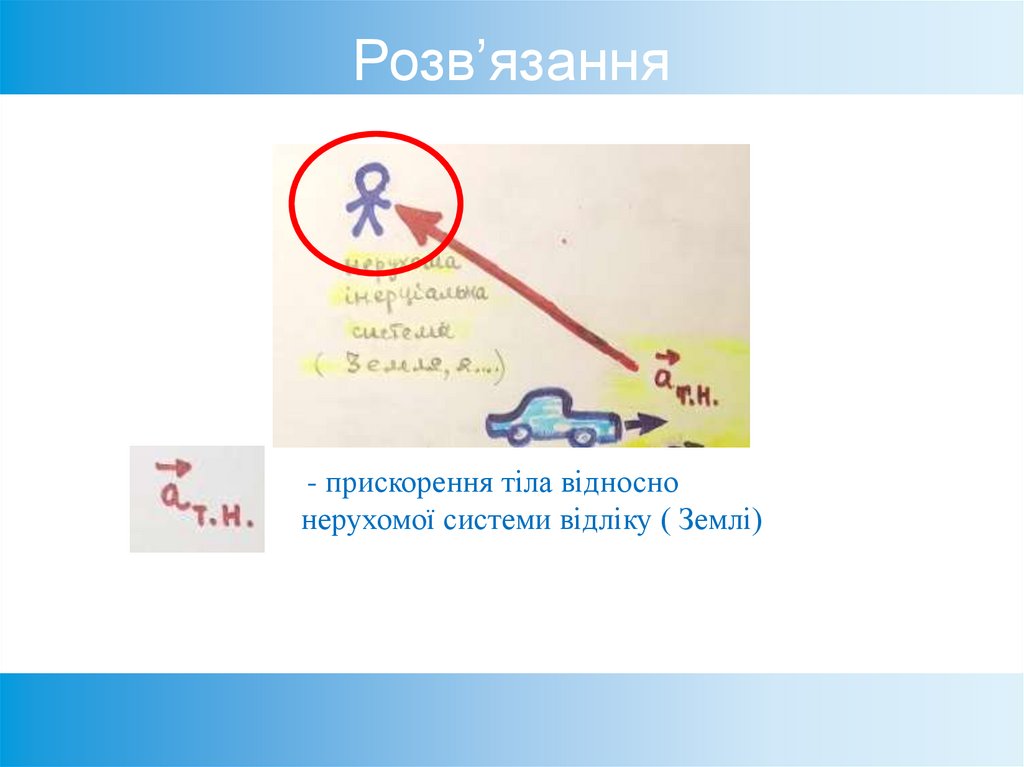
37. Розв’язання

- прискорення тіла відносно
нерухомої системи відліку ( Землі)

38. Розв’язання

- прискорення тіла відносно
рухомої системи відліку ( автобус)

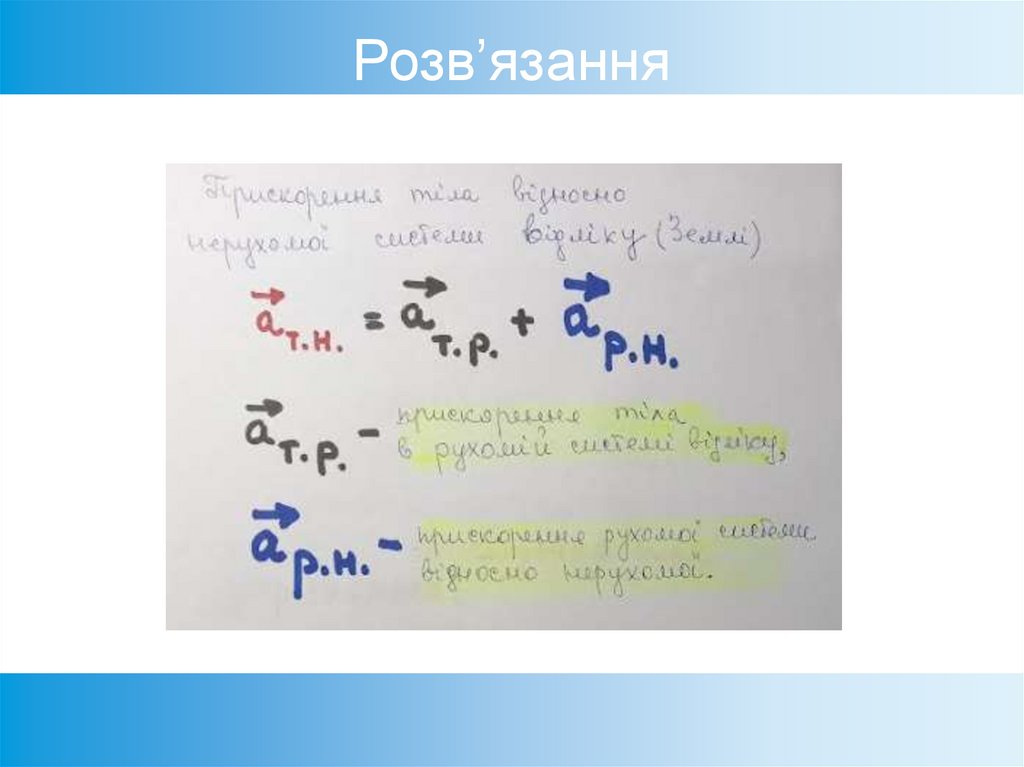
39. Розв’язання

40. Розв’язання

41. Розв’язання

42. Висновок

При переході від однієї інерціальної системи
до іншої інерціальної системи
прискорення тіла зберігається!

43. Висновок: принцип Галілея

Якщо прискорення
в усіх інерціальних системах — однакове,
то й сили в них — теж однакові.
Тому
механічні явища
в усіх інерціальних системах відліку
протікають однаково.
Це твердження називають
принципом відносності Галілея.

44. Третій закон Ньютона

→
Коли одне тіло діє на друге з деякою силою F→12,
друге тіло взаємодіє з першим з тою ж силою F21,
але протилежною за напрямком,
при чому вони прикладені до однієї і тої ж точки,
але до різних тіл,
і мають однакову фізичну природу.

45. Третій закон Ньютона

Кошик тисне
на голову жінки
→
із силою F12.
Голова тисне
на
кошик
→
із силою F21.
→
F21
→
F12

46. Третій закон Ньютона

( інше формулювання)
Да тіла взаємодіють із силами,
рівними за величиною,
але протилежними за напрямком,

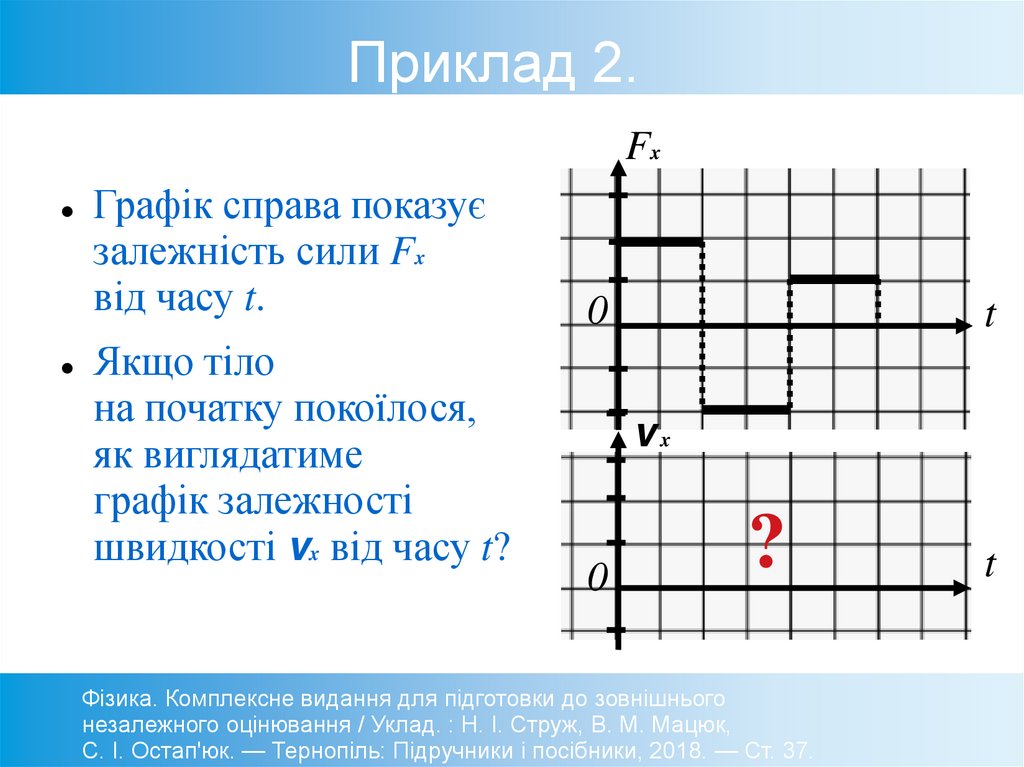
47. 48. Приклад 2.

Fx
Графік справа показує
залежність сили Fx
від часу t.
Якщо тіло
на початку покоїлося,
як виглядатиме
графік залежності
швидкості vx від часу t?
0
t
vx
0
?
Фізика. Комплексне видання для підготовки до зовнішнього
незалежного оцінювання / Уклад. : Н. І. Струж, В. М. Мацюк,
С. І. Остап'юк. — Тернопіль: Підручники і посібники, 2018. — Ст. 37.
t

49. Розв'язування

Щоб знайти швидкість, скористаймося виразом:
(1)
Для розрахунків v треба знати:
1. Прискорення тіла a.
2. Початкову швидкість тіла v 0.
Прискорення знайдемо із ІІ закону Ньютона.
(2)

50. Розв'язування

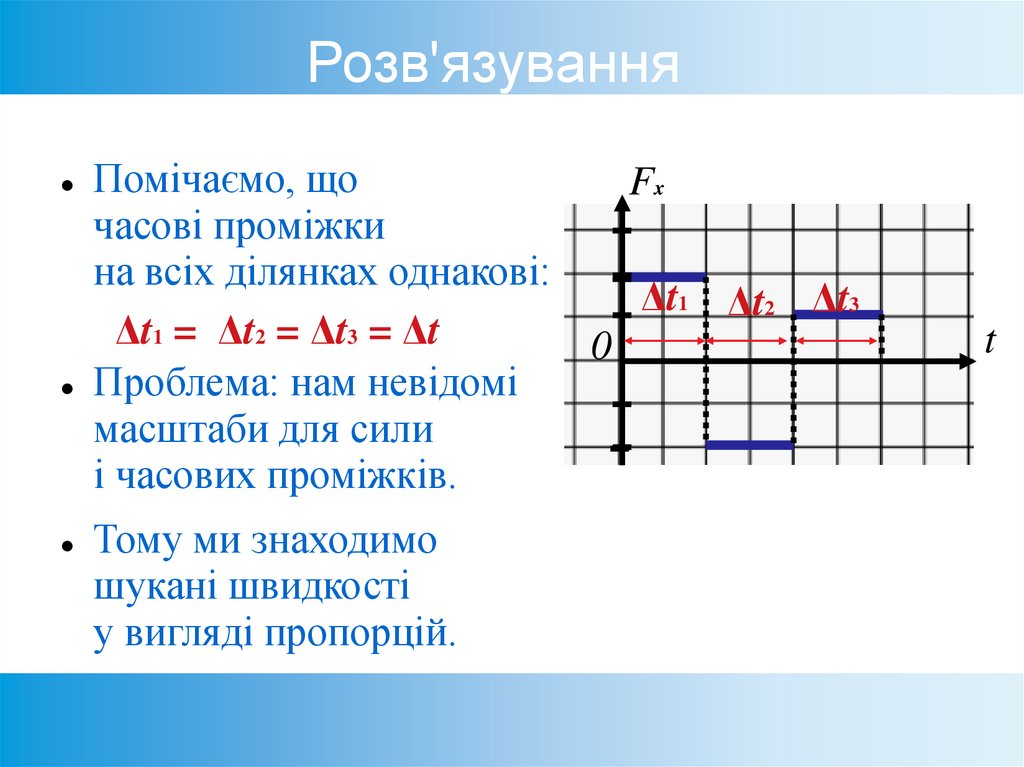
51. Розв'язування

Помічаємо, що
Fx
часові проміжки
на всіх ділянках однакові:
Δt1 Δt2 Δt3
Δt1 = Δt2 = Δt3 = Δt
0
Проблема: нам невідомі
масштаби для сили
і часових проміжків.
Тому ми знаходимо
шукані швидкості
у вигляді пропорцій.
t

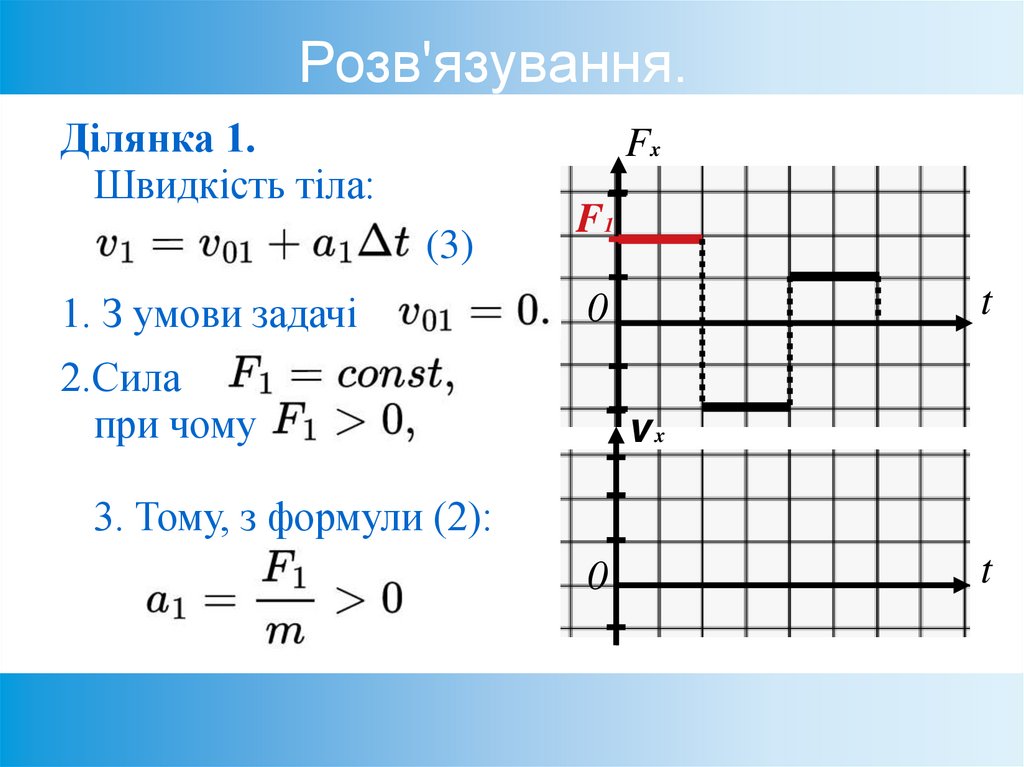
52. Розв'язування.

Ділянка 1.
Швидкість тіла:
Fx
(3)
1. З умови задачі
F1
t
0
2.Сила
при чому
vx
3. Тому, з формули (2):
0
t

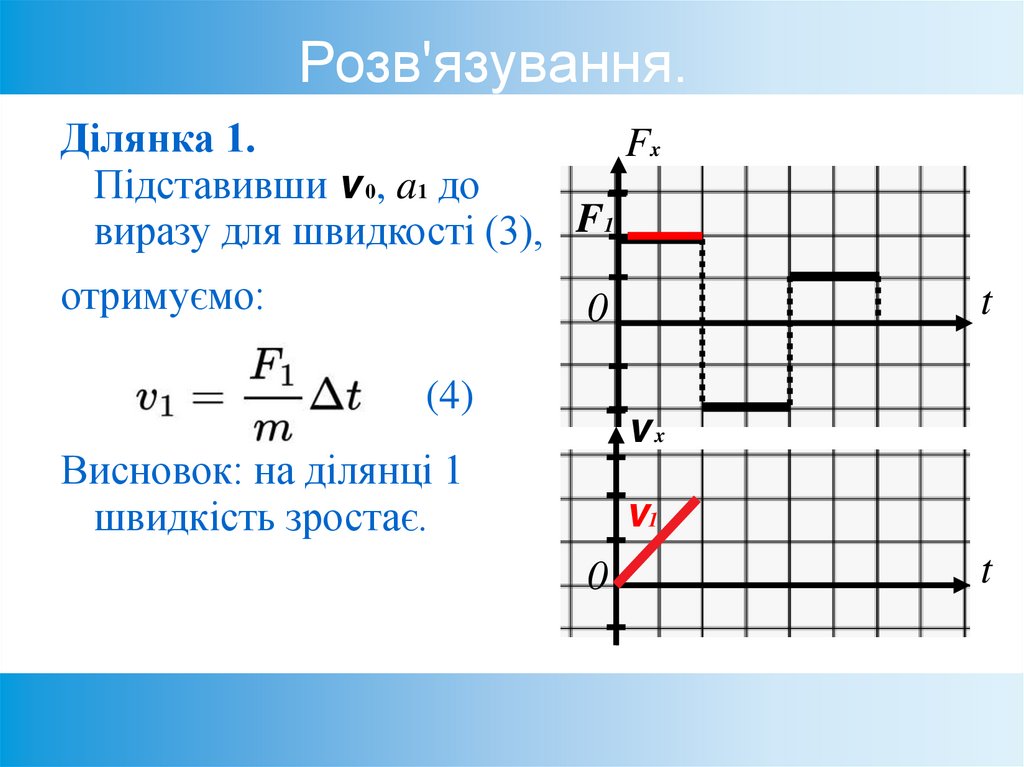
53. Розв'язування.

Ділянка 1.
Fx
Підставивши v 0, a1 до
виразу для швидкості (3), F1
отримуємо:
t
0
(4)
vx
Висновок: на ділянці 1
швидкість зростає.
v1
0
t

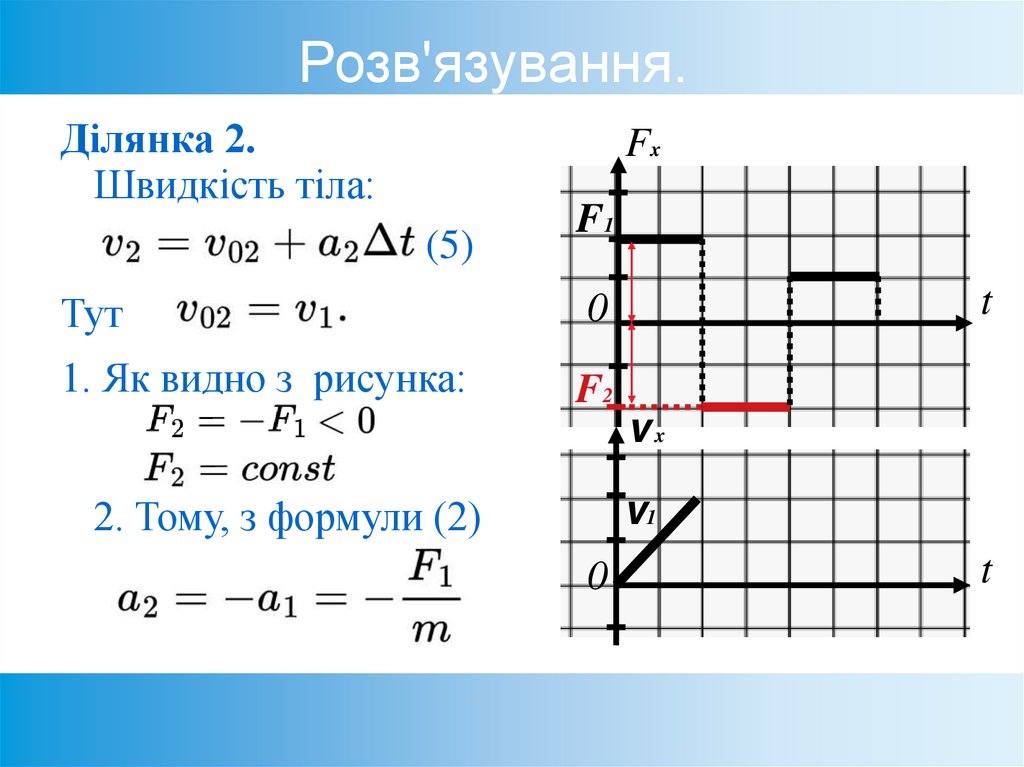
54. Розв'язування.

Ділянка 2.
Швидкість тіла:
Fx
(5)
F1
Тут
0
1. Як видно з рисунка:
F2
t
vx
2. Тому, з формули (2)
v1
0
t

55. Розв'язування.

Fx
Робимо висновок, що
швидкість на другій
ділянці спадає.
З формули (5) маємо:
F1
t
0
F2
vx
v1
Швидкість на ділянці 2
спадає до нуля:
0
t

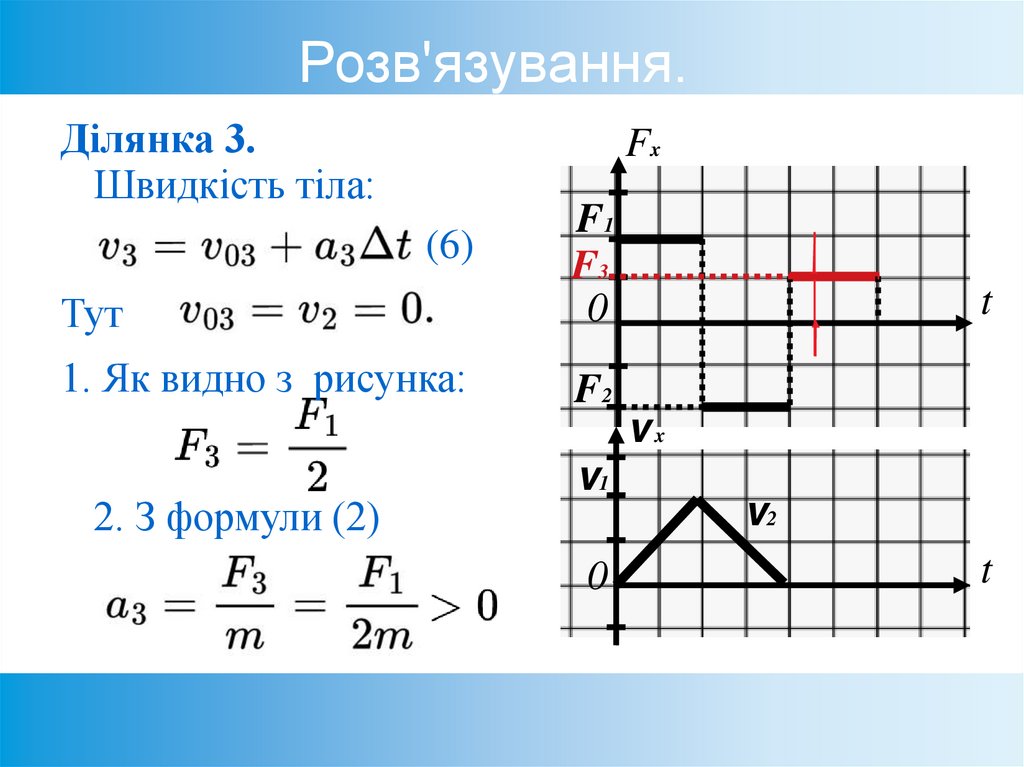
56. Розв'язування.

Ділянка 3.
Швидкість тіла:
Fx
Тут
F1
F3
0
1. Як видно з рисунка:
F2
(6)
t
vx
2. З формули (2)
v1
0
v2
t

57. Розв'язування.

Fx
Робимо висновок, що
швидкість на ділянці 3
зростає. З формули (6):
F1
F3
0
t
F2
vx
Згідно (4)
Тому
.
.
v1
0
v2
v3
t

58. Відповідь.

Залежність швидкості тіла v x
від часу t має наступний вигляд:
vx
v1
0
t

59. Приклад 3.

На тіло масою 2 кг діють сили F1 = 10 Н і
F2 = 20 Н. Кут між цими силами α = 120°.
Яке прискорення має тіло?
→
1
F
α
→
2
F
Фізика. Комплексне видання для підготовки до зовнішнього
незалежного оцінювання / Уклад. : Н. І. Струж, В. М. Мацюк,
С. І. Остап'юк. — Тернопіль: Підручники і посібники, 2018. — Ст. 38.

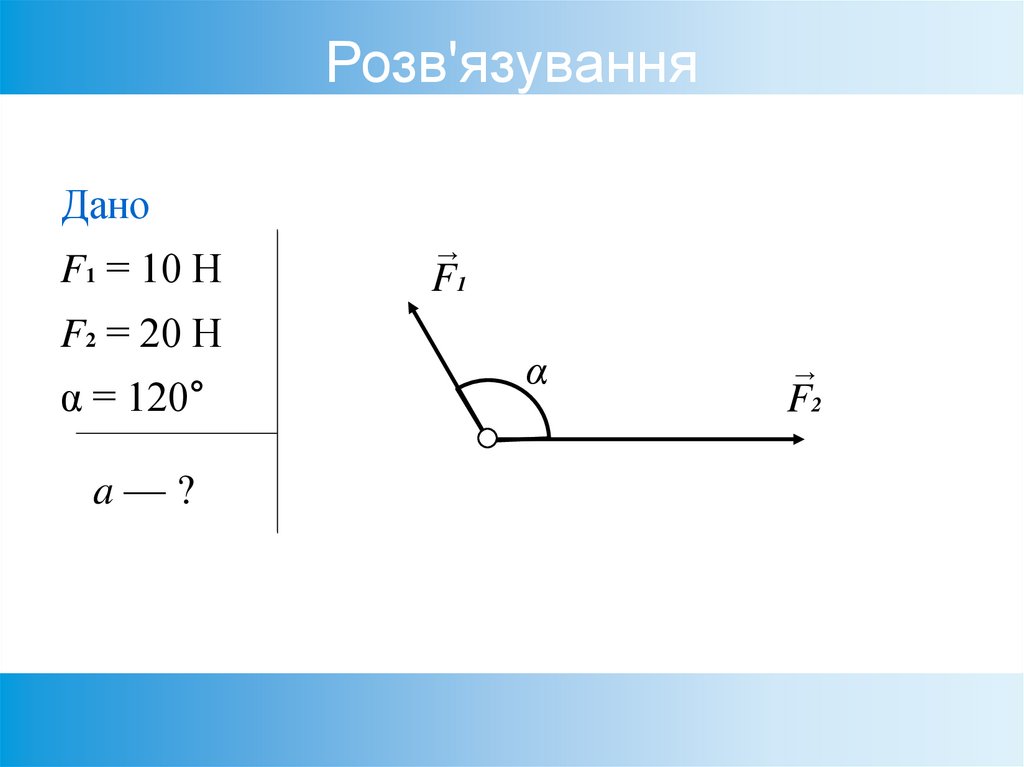
60. Розв'язування

Дано
F1 = 10 Н
F2 = 20 Н
α = 120°
a—?
→
1
F
α
→
2
F

61. Розв'язування

Прискорення а можна знайти
за ІІ законом Ньютона:
де F є рівнодійною всіх діючих сил.
За умовою задачі:
m = 2 кг
F—?

62. Розв'язування

У нашому випадку
на тіло діють 2 сили водночас.
Тому треба знайти→ модуль
→
→
рівнодійної сили F=F1+F2.
→
1
F
→
→
→
F=F1+F2 ?
α
→
2
F

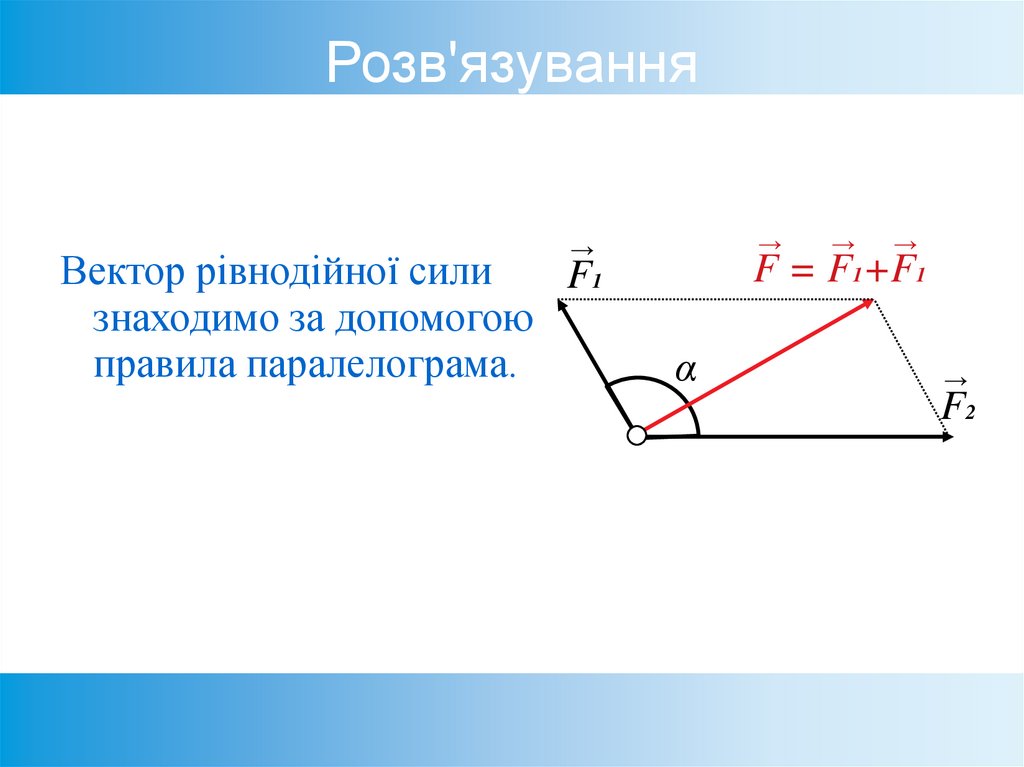
63. Розв'язування

→
→
Вектор рівнодійної сили
F1
знаходимо за допомогою
правила паралелограма.
→
→
F = F1+F1
α
→
F2

64. Розв'язування

→
→
→
Модуль рівнодійної сили F = F1+F2 —
це довжина її вектора.
Модуль F можна знайти з теореми косинусів.
→
F1
→
β
→
→
F =F1+F2
α
→
F2

65. Розв'язування

→
F1
Розв'язування
→
→
→
F =F1+F2
β
α
→
F2
β—?
Модуль рівнодійної сили
згідно теореми косинусів:

66. Розв'язування

Підставимо значення маси m та модуля сили F
до ІІ закону Ньютона і розрахуємо прискорення а:

67. Відповідь

Тіло рухається з прискоренням:

68. Приклад 4

З якою мінімальною силою має вдарити
футболіст по м'ячу, щоб той пролетів відстань
50 м? Маса м'яча становить 500 г, тривалість
удару — 20 мс. Опором повітря знехтуйте.
Фізика. Комплексне видання для підготовки до зовнішнього
незалежного оцінювання / Уклад. : Н. І. Струж, В. М. Мацюк,
С. І. Остап'юк. — Тернопіль: Підручники і посібники, 2018. — Ст. 38.

69. Задача

Дано:
m = 500 г = 0,5 кг
t = 20 мс = 20·10-3 с = 0,02 с
l = 50 м
F=?

70. Розв'язання

Силу знаходимо з другого закону Ньютона:
(1)
Маса m відома з умови.
a—?

71. Розв'язання

Прискорення за означенням дорівнює:
(2)
де v кінц — деяка швидкість, набута після удару.
v поч — швидкість до удару.
До удару м'яч покоївся, тому:
t = 0,02 с.
v кінц — ?
І швидкість v кінц повинна бути мінімальною.

72. Розв'язання

Рух м'яча — це
рух тіла, кинутого
під кутом α до горизонту.
З умови нам відома
дальність польоту м'яча l.
Відстань l пов'язана зі швидкістю v кінц:
(3), де

73. Розв'язування

З формули (3) знаходимо швидкість v кінц:
Швидкість мінімальна, коли
Звідси

74. Розв'язання

Підставляємо v 0 до формули (2):
(4)
Після чого (4) — до формули (1), і рахуємо:

75. Відповідь

М'яч ударили із силою:
Н

76. Приклад 5 (Кабардін, стор. 59).

77. Умова задачі

78. Підказка 1!

Рух краплі доречно розглядати
на двох ділянках:
1.На верхній ділянці
рух краплі прискорений;
2. На нижній ділянці
рух краплі рівномірний.

79. Підказка 2!

За умовою задачі
сила опору повітря весь час
пропорційна швидкості руху.

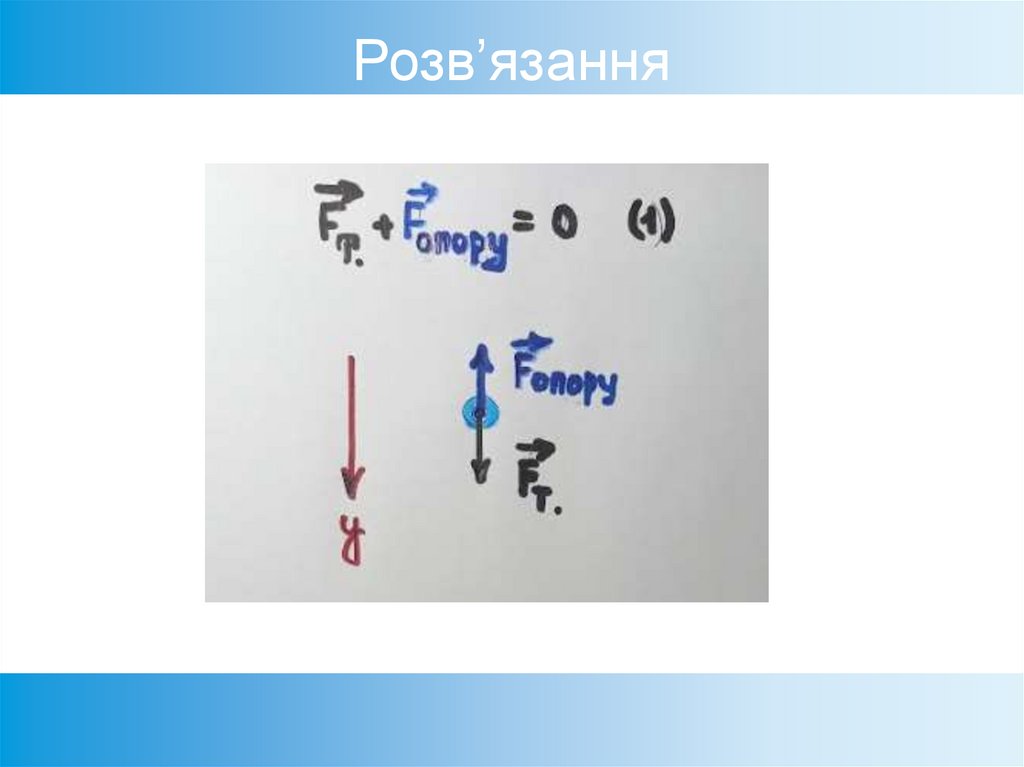
80. Розв’язання

1. На нижній ділянці (поблизу Землі) крапля
рухається зі сталою швидкістю
.
Згідно з I законом Ньютона,
це відбувається тоді,
коли рівнодійна всіх сил,
прикладених до краплі,
дорівнює 0.

81. Розв’язання

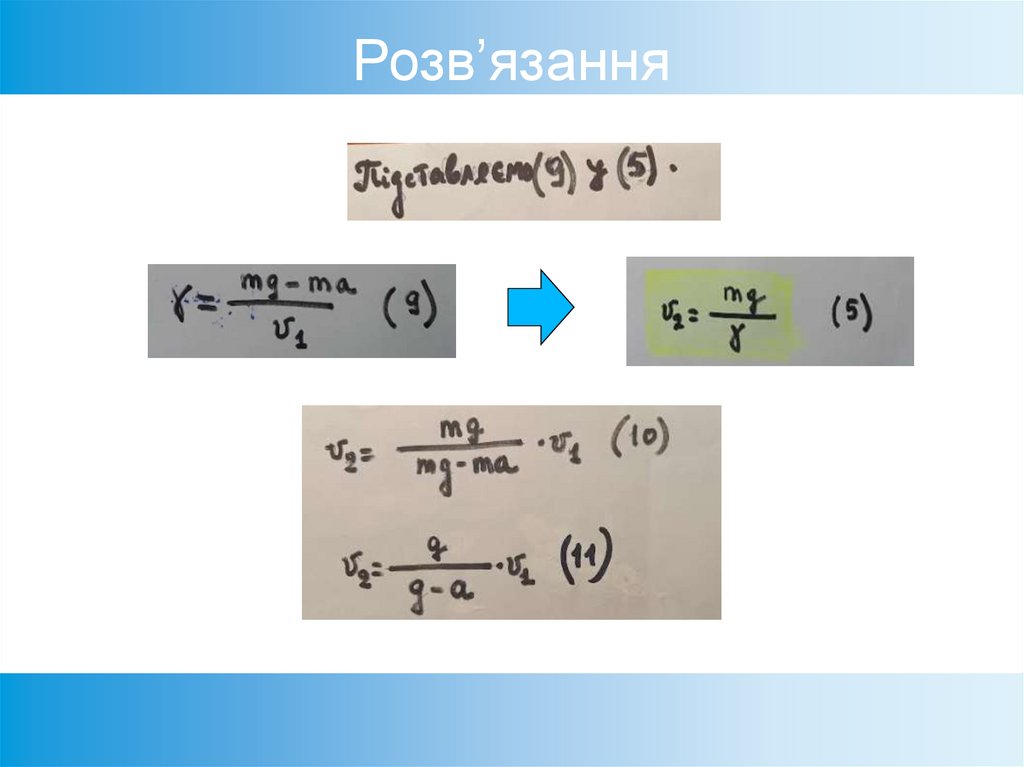
82. Розв’язання

83. Розв’язання

84. Розв’язання

85. Розв’язання

86. Розв’язання

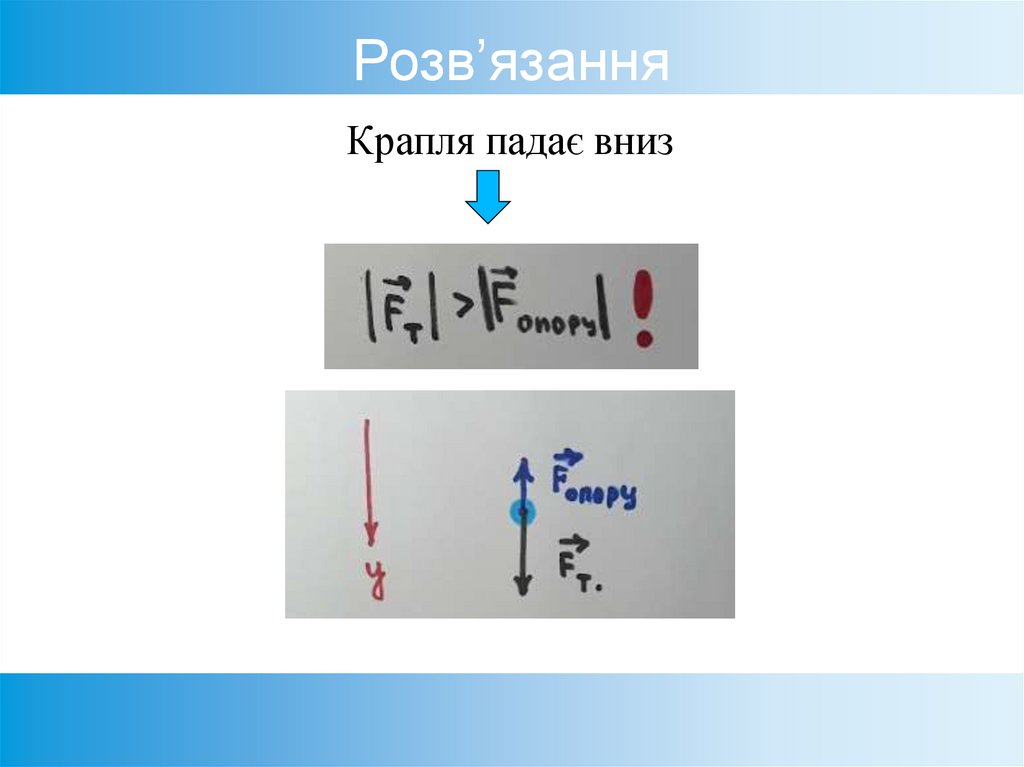
2. На верхній ділянці крапля падає вниз з
прискоренням. В деякий момент часу, коли її
прискорення
, швидкість становила
Згідно з II законом Ньютона,
це відбувається тоді,
коли рівнодійна всіх сил,
прикладених до краплі,
надає їй прискорення а .