3_1_OWF_2025

1.

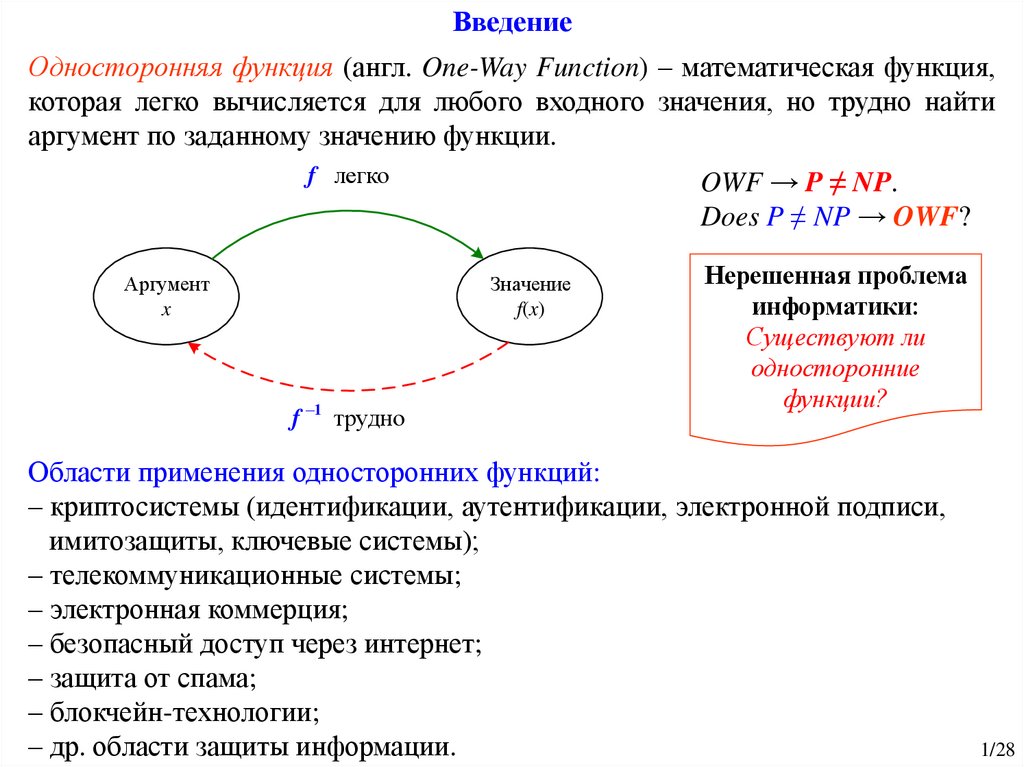
Введение
Односторонняя функция (англ. One-Way Function) – математическая функция,
которая легко вычисляется для любого входного значения, но трудно найти
аргумент по заданному значению функции.
f легко
Аргумент
x
OWF → P ≠ NP.
Does P ≠ NP → OWF?
Значение
f(x)
f –1 трудно
Нерешенная проблема
информатики:
Существуют ли
односторонние
функции?
Области применения односторонних функций:
– криптосистемы (идентификации, аутентификации, электронной подписи,
имитозащиты, ключевые системы);
– телекоммуникационные системы;
– электронная коммерция;
– безопасный доступ через интернет;
– защита от спама;
– блокчейн-технологии;
– др. области защиты информации.
1/28

2.

Вопрос 1. Классические односторонние функции
Односторонней функцией называется отображение множества всех слов
конечной длины n над конечным алфавитом, для которого существует такое
число α, что образ любого слова длины n можно вычислить за O(nα) операций,
но ни для какого числа β не существует алгоритма, вычисляющего для любого
слова длины n его прообраз за O(nβ).
Принципиальное условие f – сложность (невозможность) вычисления
обратного преобразования f –1, которое
– может не являться функцией;
– может быть неоднозначным (y = x2 : x y , x y ).
В криптосистемах используются вычислительно необратимые функции, для
которых обратное преобразование существует и однозначно, но
вычислительно нереализуемо.
2/28

3.

Односторонние функции с потайным ходом
Односторонняя функция с потайным ходом (секретом, лазейкой)
(англ. Trapdoor Function) – односторонняя функция y = fz(x) c дополнительным
свойством, что, зная информацию z о потайном ходе, вычислительно просто
определить значение х Х, удовлетворяющее уравнению fz(x) = y, однако, без
знания информации z определение значения у = fz–1(x) вычислительно
нереализуемо.
Информация z односторонняя функция с потайным ходом может служить
закрытым ключом для асимметричных криптосистем.
Например:
– RSA (патент, факторизация);
– схема Эль-Гамаля (не запатентован, дискретное логарифмирование);
– функция Рабина (факторизация, поиск квадратных корней в кольце вычетов);
– криптосистема Мак-Элиса (сложность декодирования полных линейных кодов);
– криптосистема Меркла–Хеллмана (задача о рюкзаке, нестойкая);
– и др.
3/28

4.

Функция перемножения простых чисел
Функция f принимает на вход два простых числа p и q в двоичном виде и
возвращает их произведение
n = f (p, q) = p · q.
Трудоемкость прямого вычисления порядка O(b2) битовых операций,
где b – общая длина входных данных.
Обратная задача – задача факторизации целых чисел (разложение на простые
сомножители заданного целого числа n).
Трудоемкость: ~ exp[(1.902+o(1))(ln n)1/3(ln ln n)2/3] битовых операций.
Если целые числа p, q выбирать случайно, то f не является односторонней!
Функция Рабина
Функция fRn принимает два целых числа x и n, где n – произведение двух
простых чисел p и q. На выходе – остаток от деления x2 на n:
fRn (x) = x2 mod n.
Обратная задача – вычисления квадратного корня по модулю n, что возможно
только после решения задачи факторизации числа n.
4/28

5.

Функция дискретного экспоненцирования
Функция дискретного возведения в степень f принимает в качестве аргументов
простое число p и целое x и возвращает остаток от деления некоторого aх на p:
f (x) = aх (mod p),
где x целое число от 1 до (p 1);
p очень большое простое число (2048 бит);
a образующий элемент – целое число (1 < a < p), степени которого
a1, a2, …, ap 1, взятые по mod p, равняются в некотором порядке всем числам
от 1 до p 1.
Например, для простого p = 7 можно выбрать основание a = 3, так как
a1(mod 7) = 3, a2(mod 7) = 2, a3(mod 7) = 6, a4(mod 7) = 4, a5(mod 7) = 5, a6(mod 7) = 1.
Трудоемкость прямого вычисления порядка O(b3) битовых операций,
где b – количество битов в двоичном представлении числа p.
Обратная задача – задача дискретного логарифмирования: x = loga f(x) mod p.
В теории групп: найти целое число k, где 1 ≤ k ≤ #G
удовлетворяющее уравнению αk = β, где α, β ∈ G.
αk = α ∙ ... ∙ α = β.
k раз
Трудоемкость: ~ exp[(1.902+o(1))(ln n)1/3(ln ln n)2/3] битовых операций.
5/28

6.

Кривые на проективной плоскости P2
Простейшая кривая на проективной плоскости определяется линейным
уравнением
a1x + a2y + a3z = 0
и называется линией.
Квадратичная кривая на проективной плоскости называется коником и
определяется квадратным уравнением
a1x2 + a2xy + a3y2 + a4xz + a5yz + a6z2 = 0.
Пример квадратичной кривой x2 + y2 = z2 и ее коников:
Гипербола
Парабола
Эллипс
6/28

7.

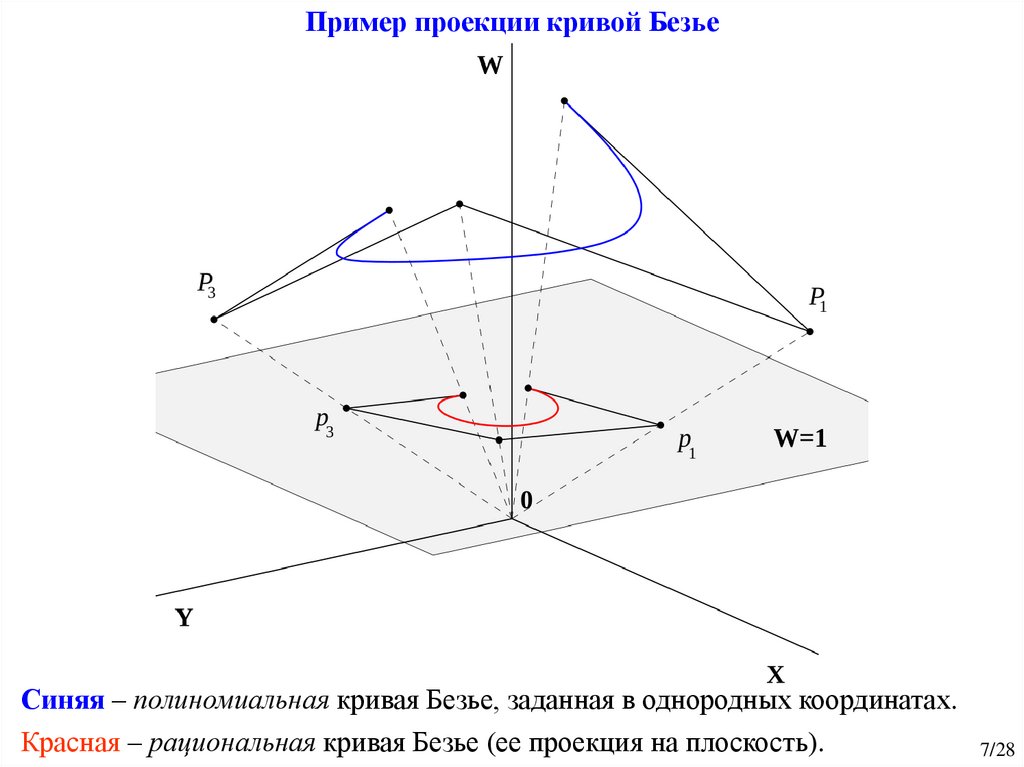
Пример проекции кривой Безье
Синяя – полиномиальная кривая Безье, заданная в однородных координатах.
Красная – рациональная кривая Безье (ее проекция на плоскость).
7/28

8.

Эллиптические кривые
(1985 г.: Виктор Миллер и Нил Коблиц – Elliptic Curve Cryptography, ECC)
Эллиптическая кривая E, определенная над базовым полем K, представляет
собой гладкую кубическую кривую в проективной плоскости P2(K)
E : a1x3+a2x2y+a3x2z+a4xy2+a5xyz+a6xz2+a7y3+a8y2z+a9yz2+a10z3 = 0 : a1, …, a10 K
вместе с выделенной K-рациональной точкой, обозначаемой ∞.
Точка на эллиптической кривой E(K) является проективной координатой
P(x, y, z) ∈ P2(K), где x, y и z удовлетворяют приведенному выше уравнению.
8/28

9.

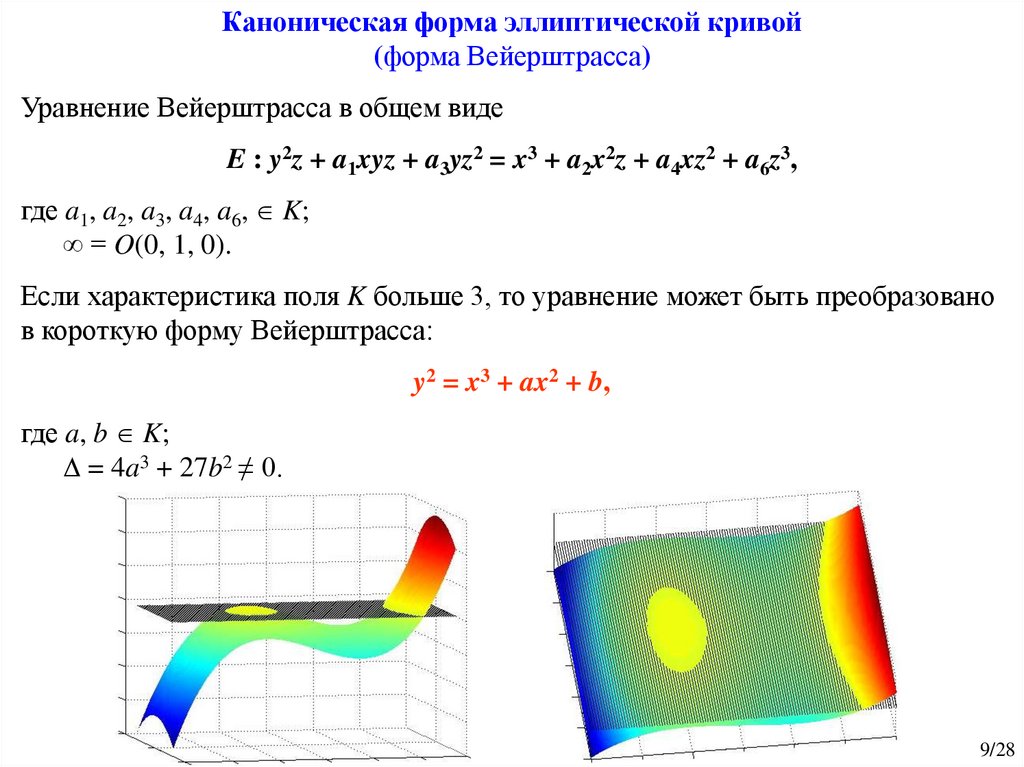
Каноническая форма эллиптической кривой
(форма Вейерштрасса)
Уравнение Вейерштрасса в общем виде
E : y2z + a1xyz + a3yz2 = x3 + a2x2z + a4xz2 + a6z3,
где a1, a2, a3, a4, a6, K;
∞ = O(0, 1, 0).
Если характеристика поля K больше 3, то уравнение может быть преобразовано
в короткую форму Вейерштрасса:
y2 = x3 + ax2 + b,
где a, b K;
= 4a3 + 27b2 ≠ 0.
9/28

10.

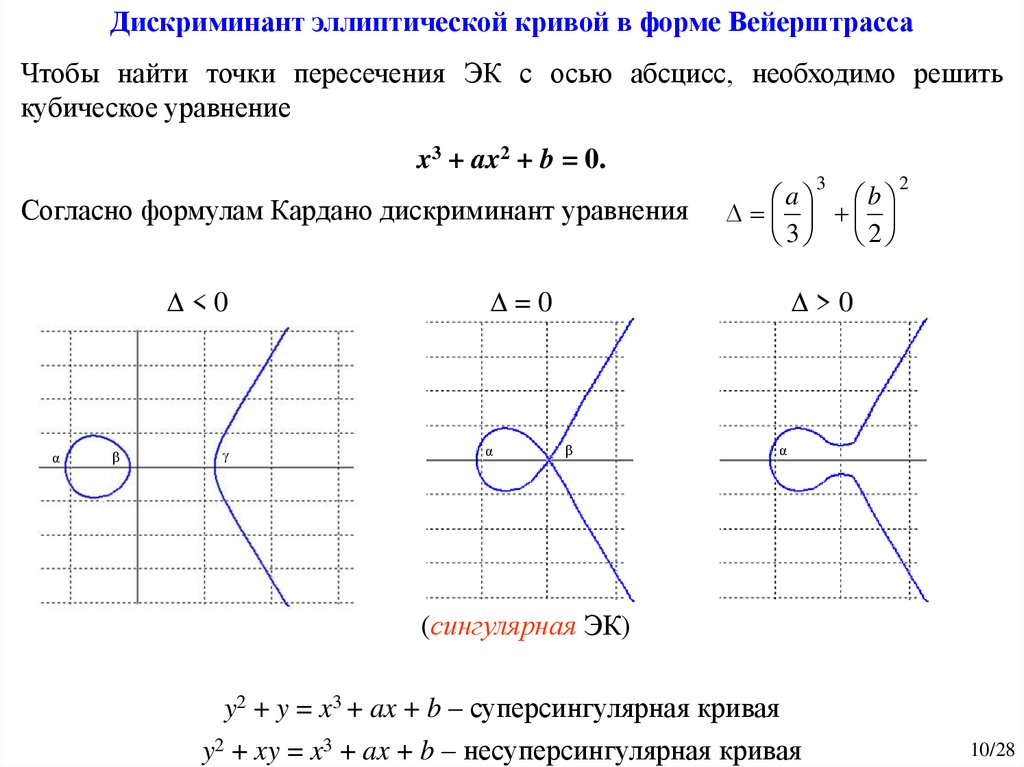
Дискриминант эллиптической кривой в форме Вейерштрасса
Чтобы найти точки пересечения ЭК с осью абсцисс, необходимо решить
кубическое уравнение
x3 + ax2 + b = 0.
3
Согласно формулам Кардано дискриминант уравнения
<0
α
β
γ
a b
3 2
=0
α
2
>0
β
α
(сингулярная ЭК)
y2 + y = x3 + ax + b – суперсингулярная кривая
y2 + xy = x3 + ax + b – несуперсингулярная кривая
10/28

11.

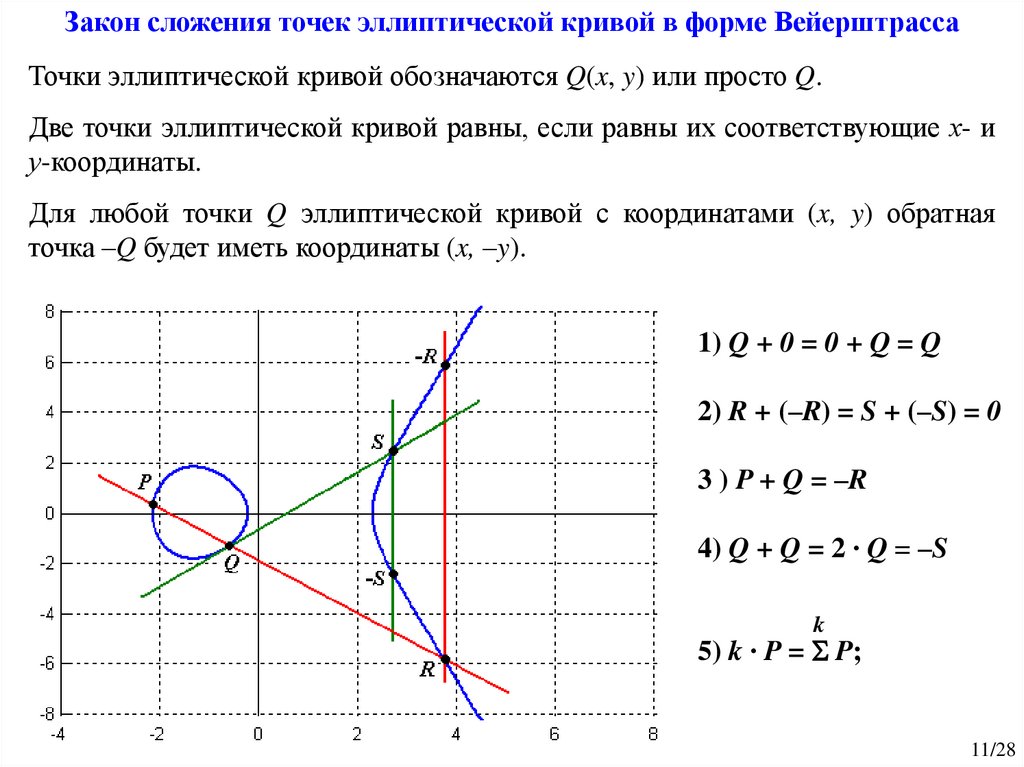
Закон сложения точек эллиптической кривой в форме Вейерштрасса
Точки эллиптической кривой обозначаются Q(x, y) или просто Q.
Две точки эллиптической кривой равны, если равны их соответствующие х- и
у-координаты.
Для любой точки Q эллиптической кривой с координатами (x, y) обратная
точка –Q будет иметь координаты (x, –y).
1) Q + 0 = 0 + Q = Q
2) R + (–R) = S + (–S) = 0
3 ) P + Q = –R
4) Q + Q = 2 ∙ Q = –S
k
5) k ∙ P = P;
11/28

12.

Односторонняя функция на основе эллиптической кривой
Исходные данные:
1) эллиптическая кривая E;
2) точка эллиптической кривой P E;
3) целое число k.
Прямая функция:
Q = k · P,
при этом для вычисления произведения по оптимальному алгоритму требуется
не более 2log2 k операций сложения.
*Например, для k = 17 : [2[2[2[2P]+P → 5 операций (4 удвоения и 1 сложение).
Обратная задача – дискретное логарифмирование на эллиптической кривой:
по заданным эллиптической кривой E, точкам P, Q E найти k.
Трудоемкость: O(q1/2) операций в группе точек эллиптической кривой, так как
решается только последовательным перебором.
Q
P
P k P
*Например, для k = 17 :
k
→ 17 операций сложения точки P (~ 2n / 2).
Таким образом, относительно легко вычислить Q по заданным k и P, но трудно
вычислить k, зная P и Q.
12/28

13.

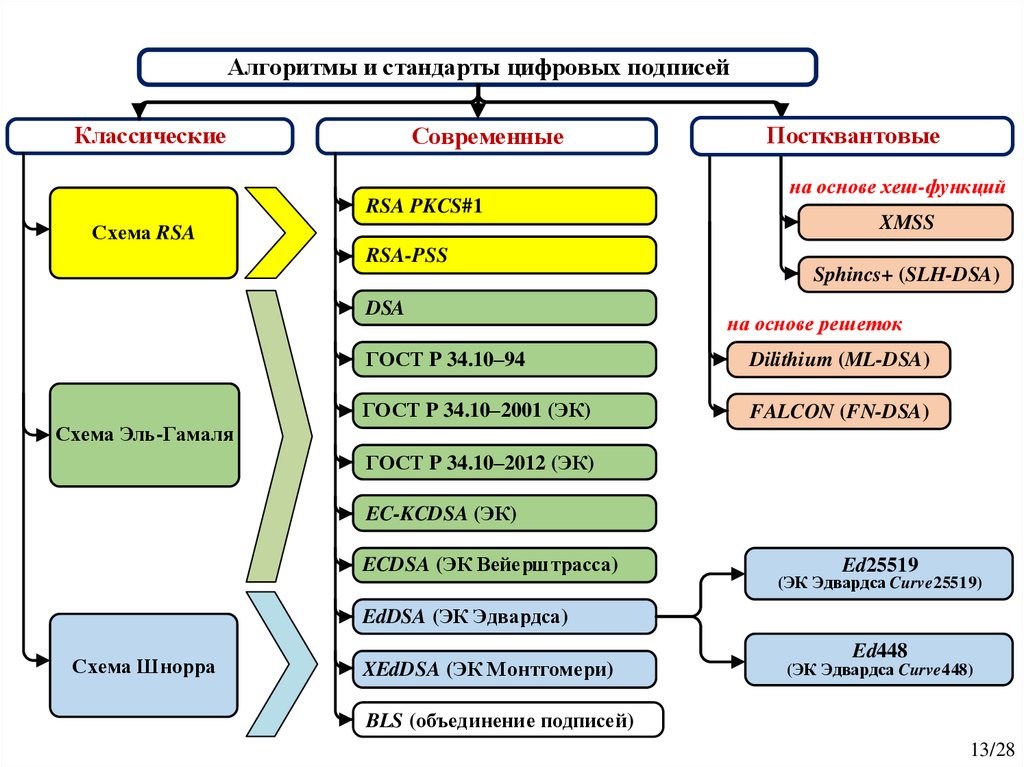
Алгоритмы и стандарты цифровых подписей
Классические
Современные
Постквантовые
на основе хеш-функций
RSA PKCS#1
Схема RSA
XMSS
RSA-PSS
Sphincs+ (SLH-DSA)
DSA
на основе решеток
ГОСТ P 34.10–94
Dilithium (ML-DSA)
ГОСТ P 34.10–2001 (ЭК)
FALCON (FN-DSA)
Схема Эль-Гамаля
ГОСТ P 34.10–2012 (ЭК)
EC-KCDSA (ЭК)
ECDSA (ЭК Вейерштрасса)
Ed25519
(ЭК Эдвардса Curve25519)
EdDSA (ЭК Эдвардса)
Схема Шнорра
XEdDSA (ЭК Монтгомери)
Ed448
(ЭК Эдвардса Curve448)
BLS (объединение подписей)
13/28

14.

Выводы по первому учебному вопросу
Основные понятия и определения:
– односторонняя функция;
– односторонняя функция с потайным ходом.
Классические претенденты на односторонние функции для криптографии:
– произведение простых чисел;
– функция Рабина;
– дискретное экспоненцирование;
– эллиптические кривые.
14/28

15.

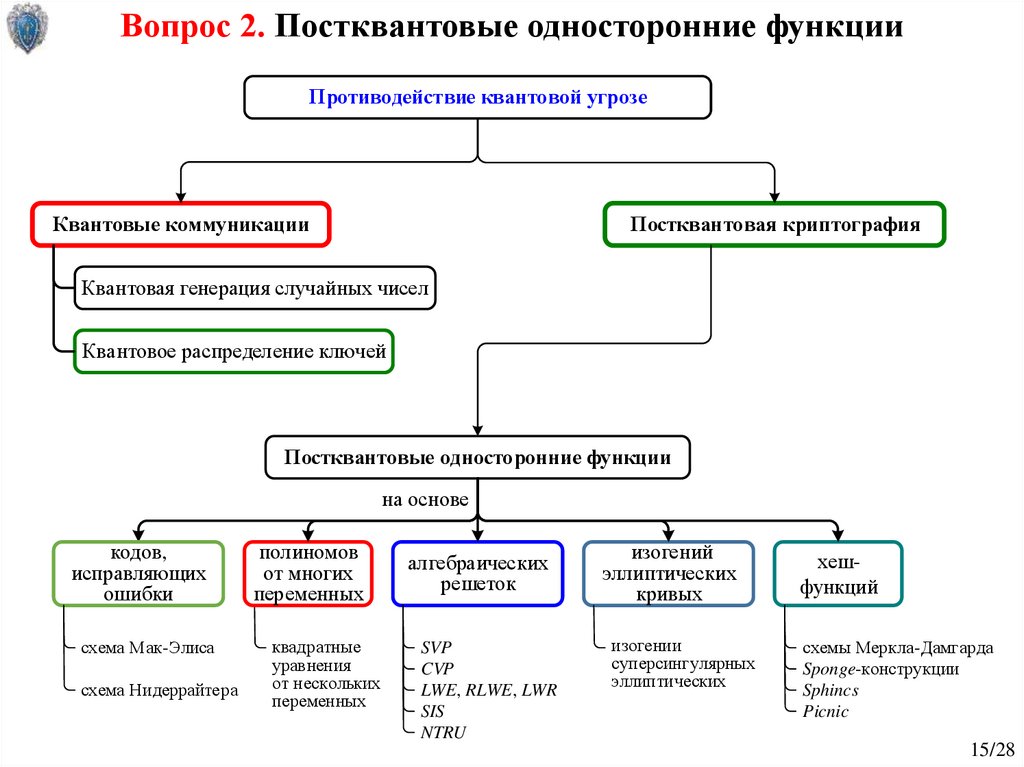
Вопрос 2. Постквантовые односторонние функции
Противодействие квантовой угрозе
Квантовые коммуникации
Постквантовая криптография
Квантовая генерация случайных чисел
Квантовое распределение ключей
Постквантовые односторонние функции
на основе
кодов,
исправляющих
ошибки
схема Мак-Элиса
схема Нидеррайтера
полиномов
от многих
переменных
квадратные
уравнения
от нескольких
переменных
алгебраических
решеток
SVP
CVP
LWE, RLWE, LWR
SIS
NTRU
изогений
эллиптических
кривых
изогении
суперсингулярных
эллиптических
хешфункций
схемы Меркла-Дамгарда
Sponge-конструкции
Sphincs
Picnic
15/28

16.

Односторонние функции на основе кодов, исправляющих ошибки
Обратная задача – декодирование случайного линейного кода.
1978 г.: криптосистема Мак-Элиса (NTRU-McElice Hybrid, BIKE, HCQ).
1986 г.: криптосистема Нидеррайтера.
2025 г.: NIST → HQC (англ. Hamming Quasi-Cyclic).
Основные достоинства и недостатки:
+ наиболее исследованный и консервативный класс постквантовых алгоритмов;
+ скорость вычисления (простые двоичные операции легко реализуются);
+ значительный вклад отечественной научной школы;
– требуются большие объемы памяти для хранения ключей.
16/28

17.

Односторонние функции на основе многомерных квадратичных полиномов
Обратная задача – решение нелинейной системы уравнений над конечным полем
(в общем случае NP-полная).
Многомерный полином – многочлен от нескольких переменных.
Известные примеры:
– функция Мацумото-Имаи, предложенная в 1988 г. (взломана в 1995 г.);
– функция, основанная на скрытых уравнениях поля (англ. Hidden Fields
Equations, HFE), предложенная в 1996 г. Ж. Патариным (взломана 2005 г.);
– функция UOV, предложенная в 1998 г. Ж. Патариным и др.
Основные достоинства и недостатки:
+ скорость вычисления;
+ низкие требования к вычислительным ресурсам;
– требуются большие объемы памяти для хранения ключей;
– обратные преобразования должны сохраняться в секрете;
– печальный опыт неудачных синтезных решений (отсутствие доказательств
стойкости).
17/28

18.

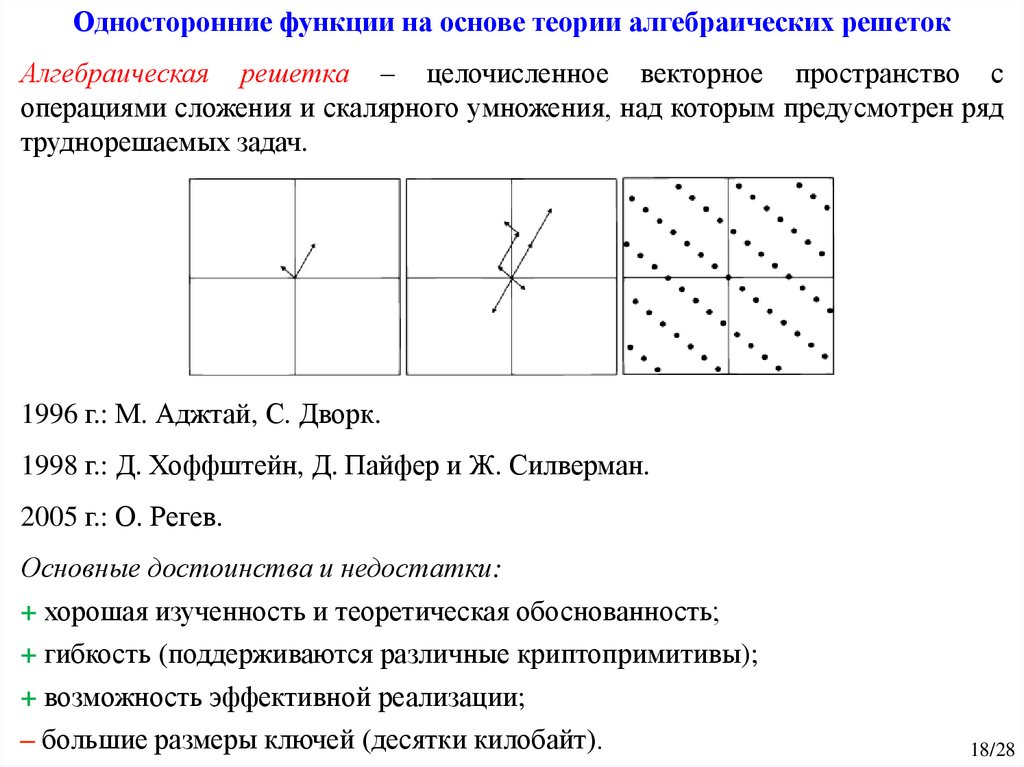
Односторонние функции на основе теории алгебраических решеток
Алгебраическая решетка – целочисленное векторное пространство с
операциями сложения и скалярного умножения, над которым предусмотрен ряд
труднорешаемых задач.
1996 г.: М. Аджтай, С. Дворк.
1998 г.: Д. Хоффштейн, Д. Пайфер и Ж. Силверман.
2005 г.: О. Регев.
Основные достоинства и недостатки:
+ хорошая изученность и теоретическая обоснованность;
+ гибкость (поддерживаются различные криптопримитивы);
+ возможность эффективной реализации;
– большие размеры ключей (десятки килобайт).
18/28

19.

Труднорешаемые задачи на основе решеток
– задача поиска кратчайшего вектора
(англ. Shortest Vector Problem, SVP): найти в
заданном базисе решетки ненулевой вектор
минимальной длины;
– задача поиска ближайшего вектора
(англ. Closest Vector Problem, CVP): найти вектор в
решетке по заданному базису и некоторому вектору,
не принадлежащему решетке, при этом схожего по
длине с заданным вектором;
– задача декодирования ограниченного расстояния
(англ. Bounded Distance Decoding, BDD): найти
ближайший к заданной точке вектор в решетке;
– задача поиска наименьшего целочисленного
решение линейных уравнений
(англ. Short Integer Solution, SIS);
– задача обучения с ошибками
(англ. Learning With Errors, LWE): найти вектор при
известной малой ошибке.
19/28

20.

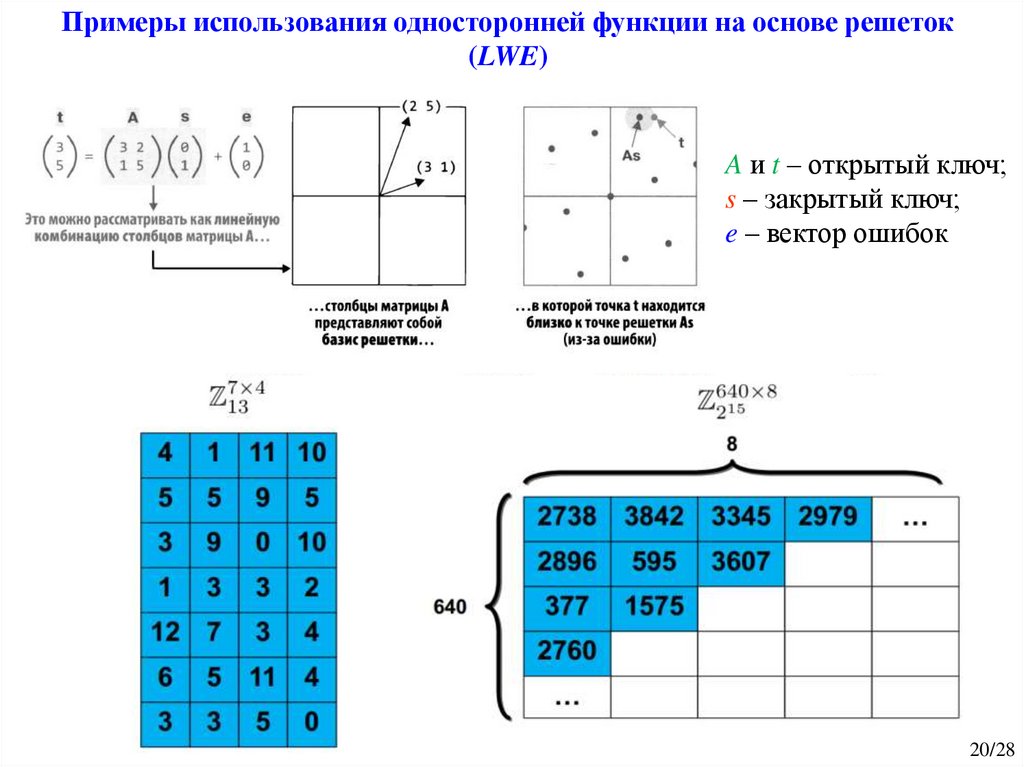
Примеры использования односторонней функции на основе решеток
(LWE)
A и t – открытый ключ;
s – закрытый ключ;
e – вектор ошибок
20/28

21.

Односторонние функции на основе изогений
суперсингулярных эллиптических кривых
Обратная задача – поиск пути в графе изогений между суперсингулярными
эллиптическими кривыми над конечным полем.
1997 г.: Кувэнь.
2006 г.: Чарльз–Горен–Лоутер.
2006 г.: Ростовцев–Столбунов.
2011 г.: де Фео, Яо (SIDH, SIKE).
Основные достоинства и недостатки:
+ изученный алгебро-геометрический аппарат;
+ малые размеры ключей;
+ поддержка совершенной прямой секретности;
– низкое быстродействие (большая вычислительная сложность);
– невозможность использования долговременных ключей без дополнительных
мер защиты.
21/28

22.

Изогения эллиптических кривых
Изогения – рациональное отображение эллиптических кривых ϕ : E1(K) → E2(K)
с коэффициентами из поля K, которое сохраняет точку бесконечности, т. е.
такое, что ϕ(∞) = ∞.
Если на эллиптической кривой E1(K) выбрать любые две точки A1, B1 и
отобразить их в точки A2 = ϕ(A1), B2 = ϕ(B1) на эллиптической кривой E2(K),
тогда то же самое отображение обязательно переведет точку С1 = A1 + B1
именно в точку С2 = A2 + B2:
ϕ(С1) = ϕ(A1 + B1) = ϕ(A1) + ϕ(B1) = A2 + B2 = C2
Теорема Тейта (Tate’s Theorem):
Две кривые над одним конечным полем
изогенны тогда и только тогда, когда
порядки их групп равны (одинаковое число точек).
Изогения ϕ :