Similar presentations:
Статистическое изучение рядов динамики
1. Статистическое изучение рядов динамики
1.2.
3.
4.
5.
Понятие о статистических рядах динамики
Показатели временных рядов
Методы выявления и описания тренд составляющей
динамического ряда
Методы выявления и описания сезонной составляющей
динамического ряда
Методы измерения колеблемости и устойчивости уровней
ряда
2. Понятие о статистических рядах динамики
3.
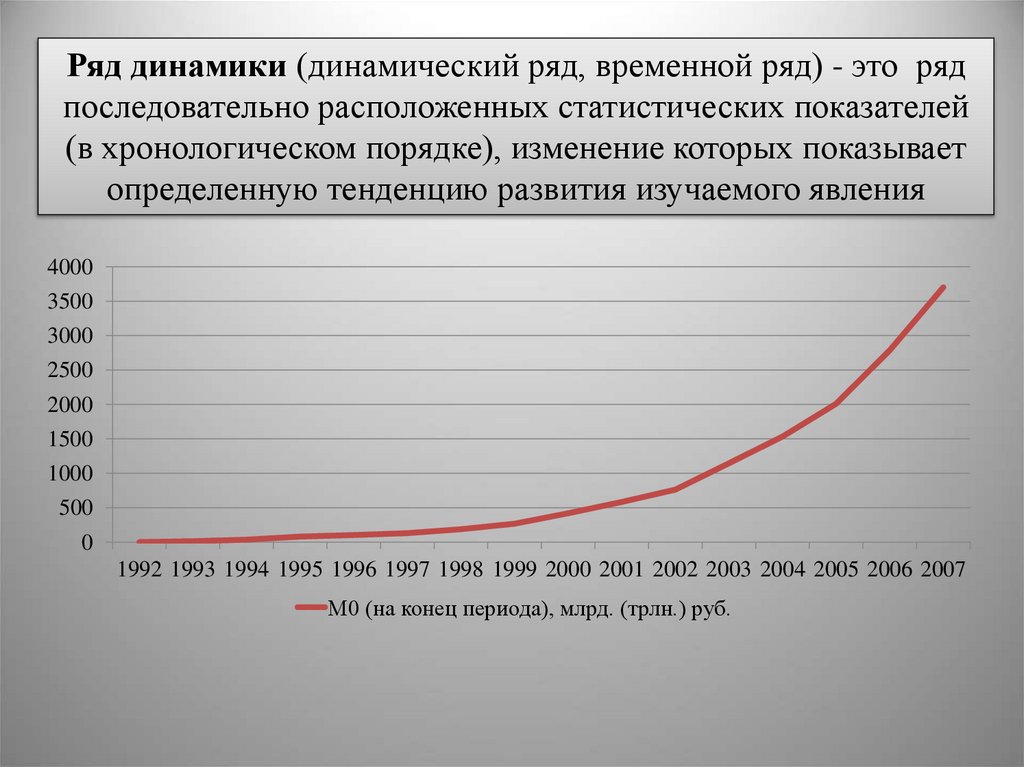
Ряд динамики (динамический ряд, временной ряд) - это рядпоследовательно расположенных статистических показателей
(в хронологическом порядке), изменение которых показывает
определенную тенденцию развития изучаемого явления
4000
3500
3000
2500
2000
1500
1000
500
0
1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007
М0 (на конец периода), млрд. (трлн.) руб.
4.
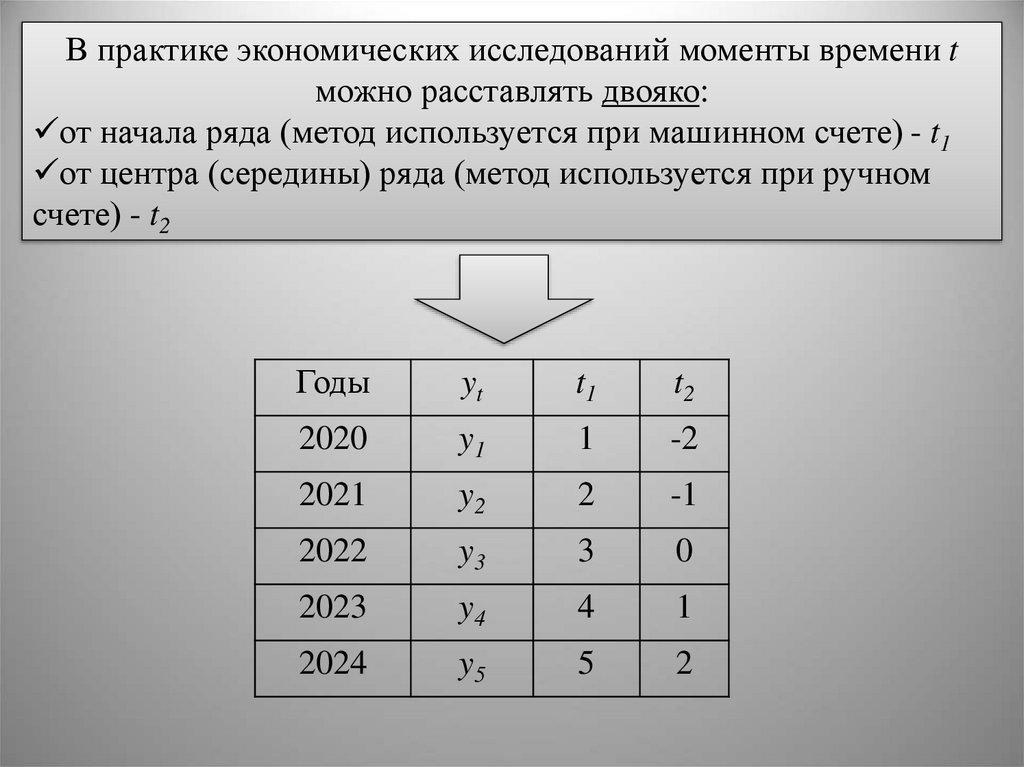
В практике экономических исследований моменты времени tможно расставлять двояко:
от начала ряда (метод используется при машинном счете) - t1
от центра (середины) ряда (метод используется при ручном
счете) - t2
Годы
yt
t1
t2
2020
y1
1
-2
2021
y2
2
-1
2022
y3
3
0
2023
y4
4
1
2024
y5
5
2
5.
(многомерный)комплексный ряд
динамики
(одномерный)
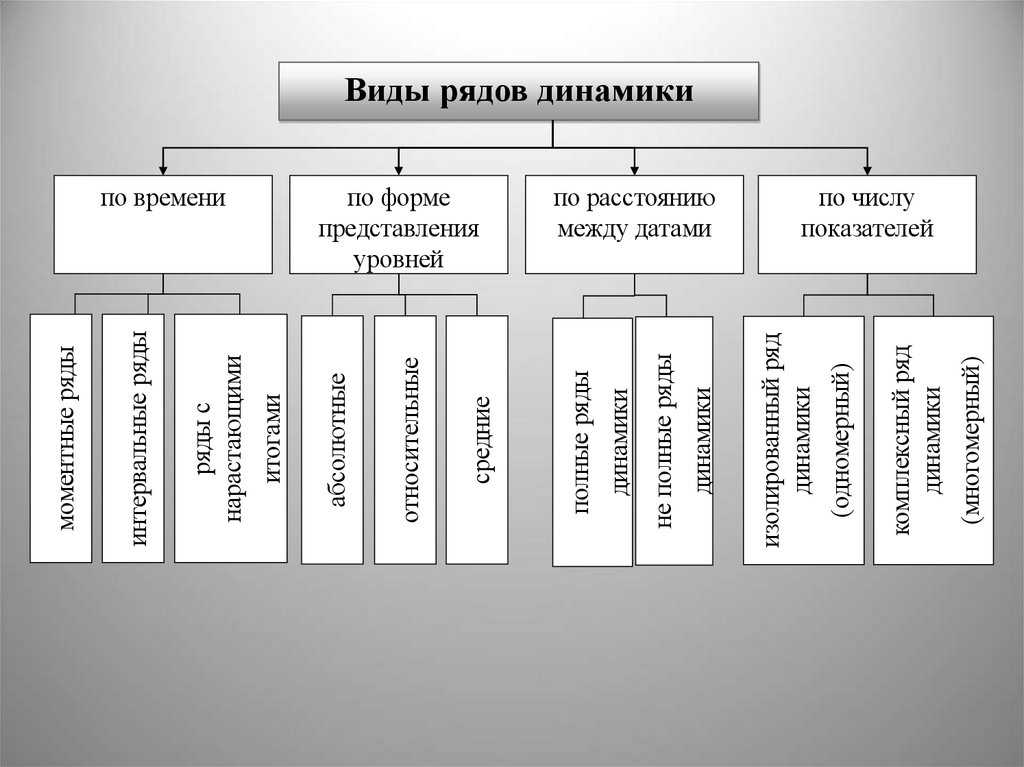
по расстоянию
между датами
изолированный ряд
динамики
динамики
не полные ряды
динамики
по форме
представления
уровней
полные ряды
средние
относительные
по времени
абсолютные
итогами
ряды с
нарастающими
интервальные ряды
моментные ряды
Виды рядов динамики
по числу
показателей
6.
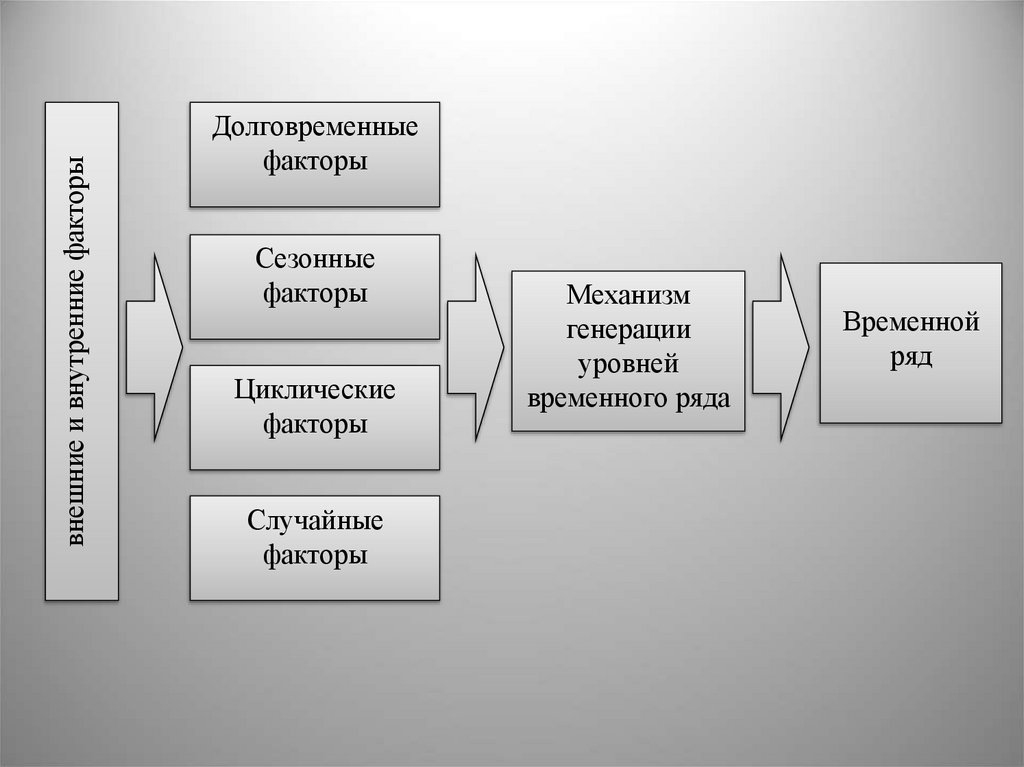
внешние и внутренние факторыДолговременные
факторы
Сезонные
факторы
Циклические
факторы
Случайные
факторы
Механизм
генерации
уровней
временного ряда
Временной
ряд
7.
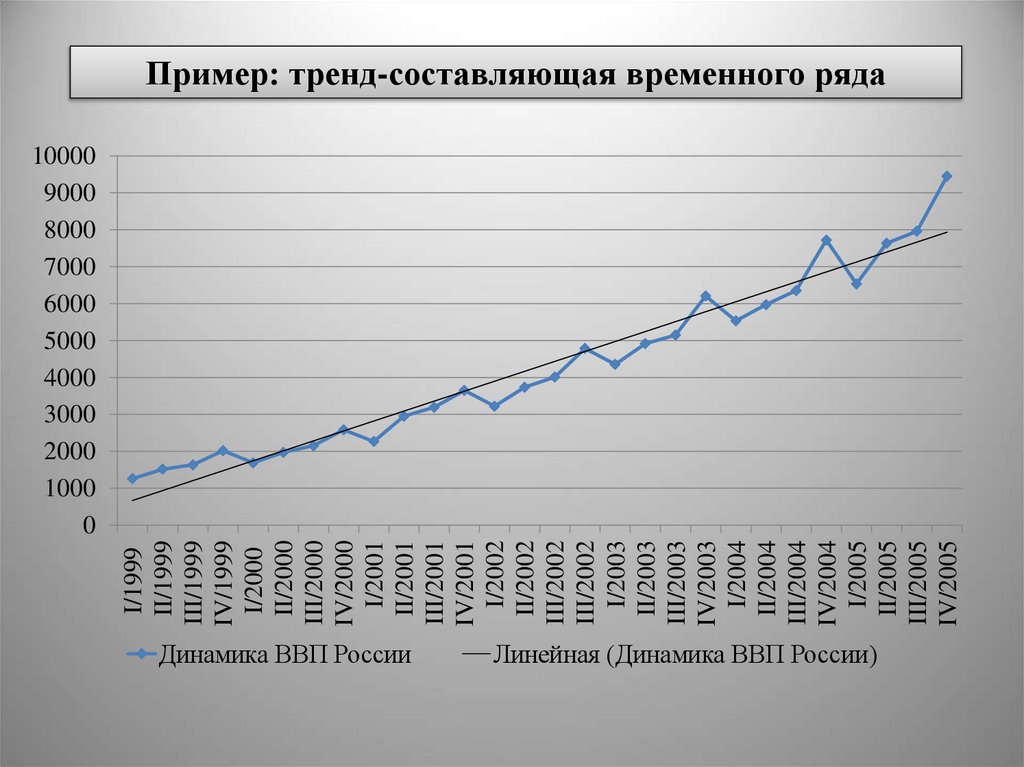
Составляющие динамического рядаY(t) = T(t) + S(t) + Z(t) + (t)
T(t) – тренд, плавно меняющаяся компонента, описывающая
чистое влияние долговременных факторов
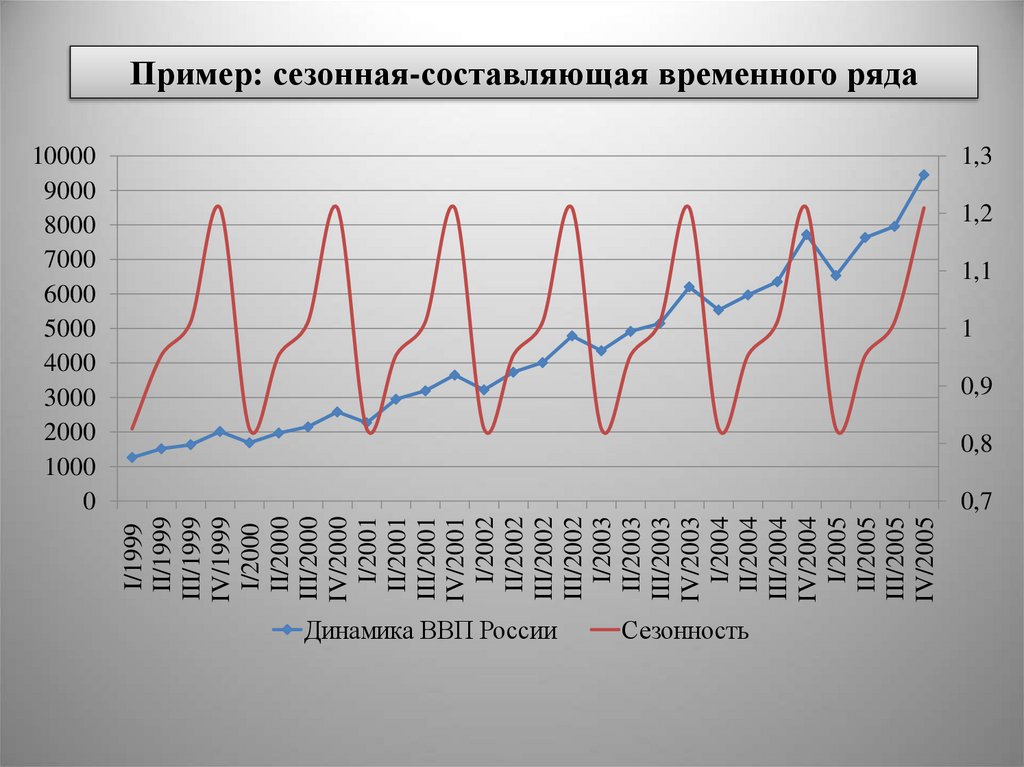
S(t) – сезонная компонента, отражающая повторяемость
социально-экономических процессов внутри года
Z(t) – циклическая компонента, отражающая повторяемость
социально-экономических процессов в течение длительных
периодов
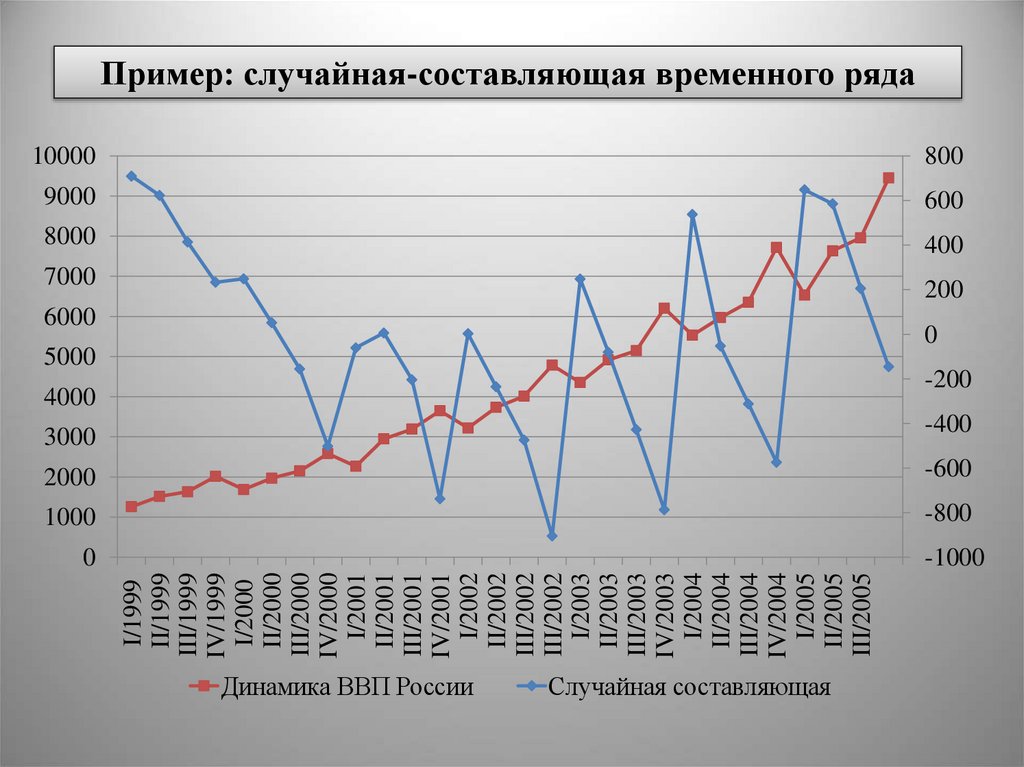
(t) – случайная компонента («остатков», «ошибок»),
отражающая влияние не поддающихся учету и регистрации
случайных факторов
8.
I/1999II/1999
III/1999
IV/1999
I/2000
II/2000
III/2000
IV/2000
I/2001
II/2001
III/2001
IV/2001
I/2002
II/2002
III/2002
III/2002
I/2003
II/2003
III/2003
IV/2003
I/2004
II/2004
III/2004
IV/2004
I/2005
II/2005
III/2005
IV/2005
Пример: тренд-составляющая временного ряда
10000
9000
8000
7000
6000
5000
4000
3000
2000
1000
0
Динамика ВВП России
Линейная (Динамика ВВП России)
9.
I/1999II/1999
III/1999
IV/1999
I/2000
II/2000
III/2000
IV/2000
I/2001
II/2001
III/2001
IV/2001
I/2002
II/2002
III/2002
III/2002
I/2003
II/2003
III/2003
IV/2003
I/2004
II/2004
III/2004
IV/2004
I/2005
II/2005
III/2005
IV/2005
Пример: сезонная-составляющая временного ряда
10000
9000
8000
7000
6000
5000
4000
3000
2000
1000
0
1,3
1,2
1,1
1
0,9
0,8
0,7
Динамика ВВП России
Сезонность
10.
I/1999II/1999
III/1999
IV/1999
I/2000
II/2000
III/2000
IV/2000
I/2001
II/2001
III/2001
IV/2001
I/2002
II/2002
III/2002
III/2002
I/2003
II/2003
III/2003
IV/2003
I/2004
II/2004
III/2004
IV/2004
I/2005
II/2005
III/2005
Пример: случайная-составляющая временного ряда
10000
800
9000
600
8000
400
7000
200
6000
5000
0
4000
-200
3000
-400
2000
-600
1000
-800
0
-1000
Динамика ВВП России
Случайная составляющая
11. Задачами анализа временных рядов являются:
1. Выявление соответствующей составляющейдинамического ряда;
2. Описание выявленной составляющей;
3. Оценка качества построенной модели;
4. Прогнозирование будущих значений показателя с учетом
соответствующих составляющих.
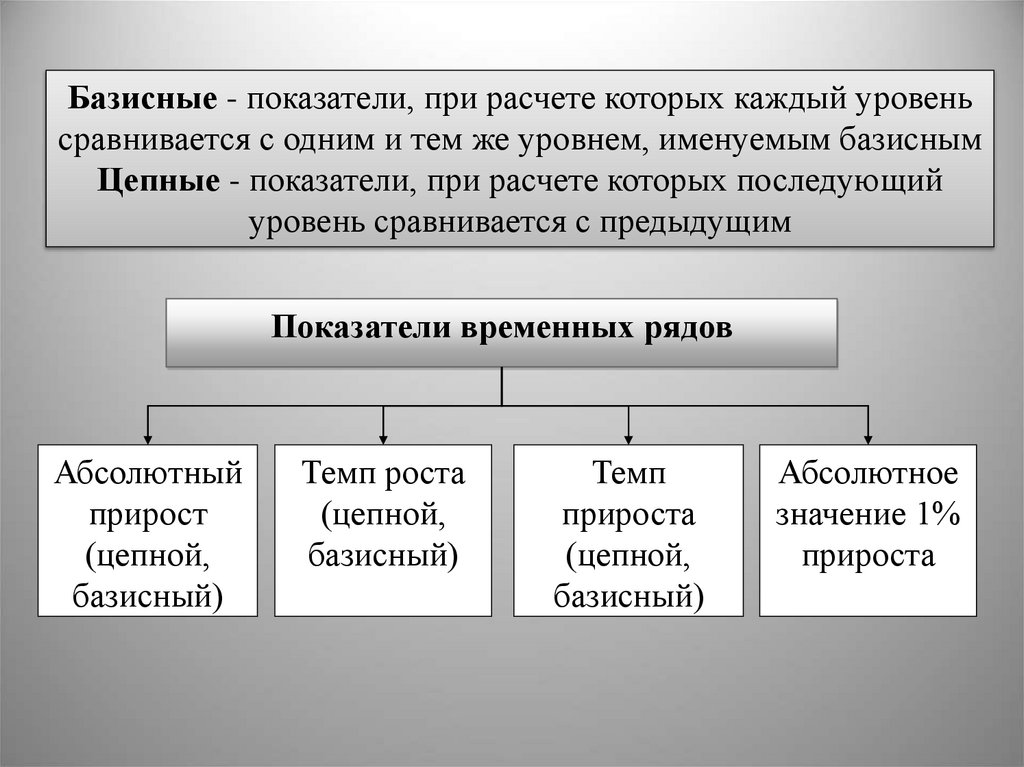
12. Показатели временных рядов
13.
Базисные - показатели, при расчете которых каждый уровеньсравнивается с одним и тем же уровнем, именуемым базисным
Цепные - показатели, при расчете которых последующий
уровень сравнивается с предыдущим
Показатели временных рядов
Абсолютный
прирост
(цепной,
базисный)
Темп роста
(цепной,
базисный)
Темп
прироста
(цепной,
базисный)
Абсолютное
значение 1%
прироста
14.
Абсолютный приростЦепной
Базисный
Измеряются в тех же единицах, что и сам показатель.
Характеризуют скорость изменения показателя. Показывает, на
сколько данный уровень ряда превышает уровень, взятый за
базу сравнения.
Цепные и базисные абсолютные приросты взаимосвязаны:
сумма последовательных цепных приростов равна
соответствующему базисному приросту за весь период
15.
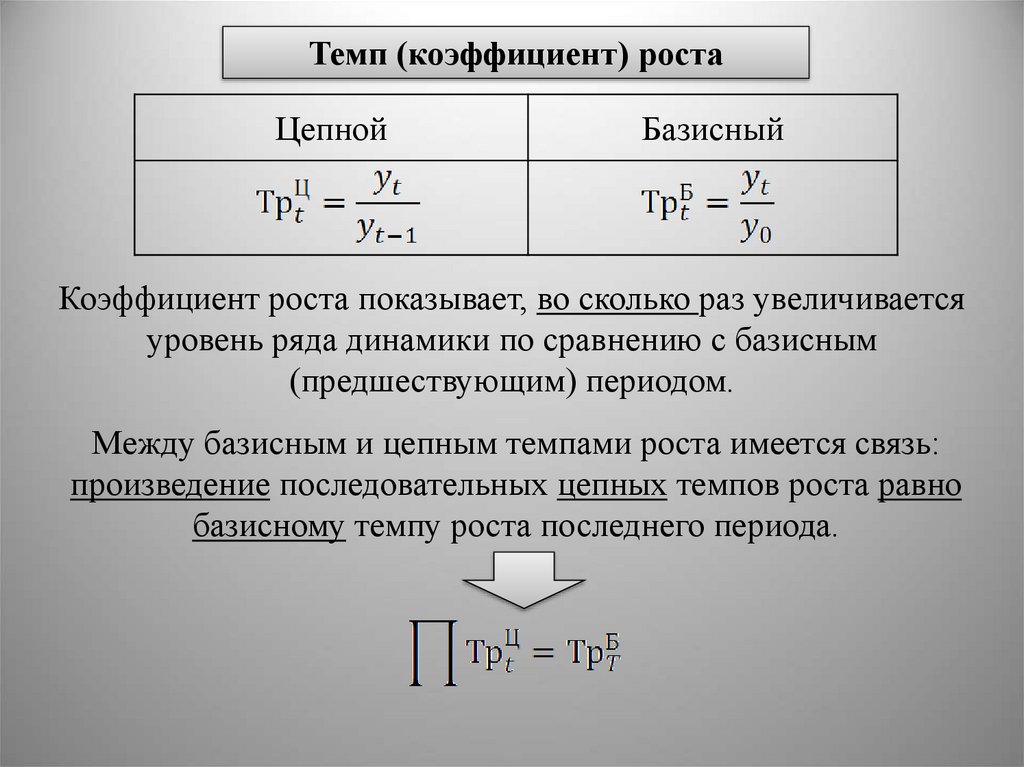
Темп (коэффициент) ростаЦепной
Базисный
Коэффициент роста показывает, во сколько раз увеличивается
уровень ряда динамики по сравнению с базисным
(предшествующим) периодом.
Между базисным и цепным темпами роста имеется связь:
произведение последовательных цепных темпов роста равно
базисному темпу роста последнего периода.
16.
Темп (коэффициент) приростаЦепной
Базисный
Показывает на сколько процентов изменился сравниваемый
уровень относительно базисного уровня
Темп прироста также можно определить как процентное
отношение абсолютного прироста к тому уровню, по
сравнению с которым рассчитан абсолютный прирост.
17.
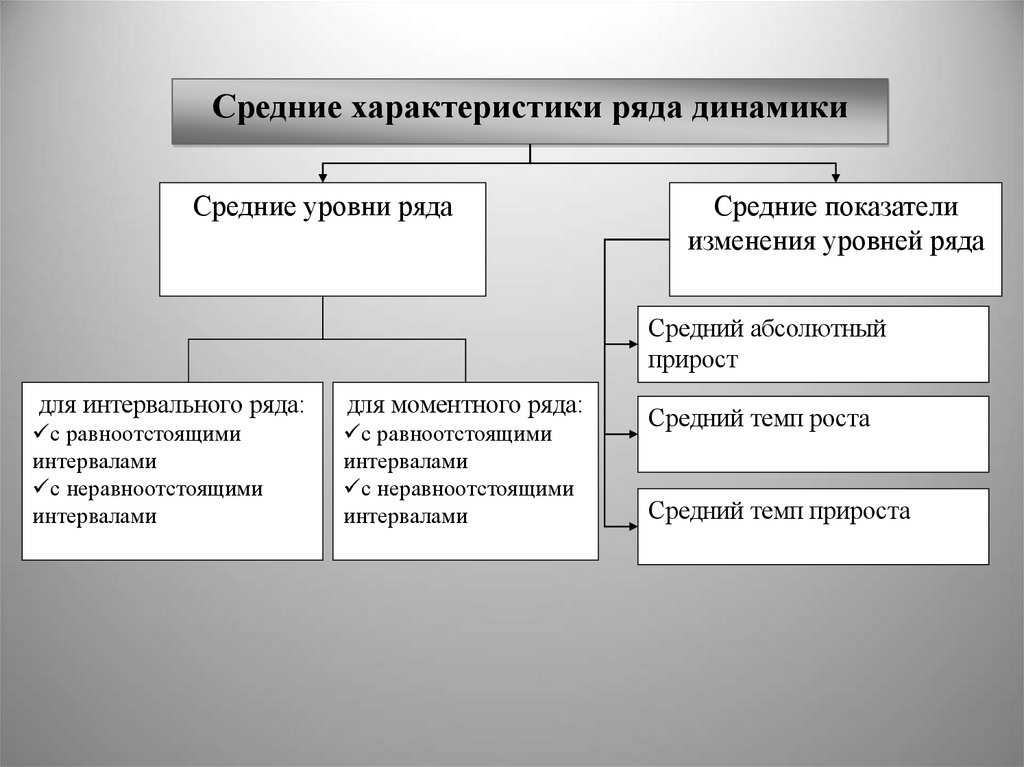
Средние характеристики ряда динамикиСредние уровни ряда
Средние показатели
изменения уровней ряда
Средний абсолютный
прирост
для интервального ряда:
для моментного ряда:
с равноотстоящими
интервалами
с неравноотстоящими
интервалами
с равноотстоящими
интервалами
с неравноотстоящими
интервалами
Средний темп роста
Средний темп прироста
18.
Вид среднейФормула расчета
В интервальном ряду с равными
интервалами
В интервальном и моментном
ряду с неравными интервалами
В моментном ряду с
равностоящими датами
Средний абсолютный прирост
Средний темп роста
Средний темп прироста
или
или
19. Методы выявления и описания тренд составляющей динамического ряда
20.
Простейшие методы выявления тенденцииво временном ряду:
Графический метод - построение кривой. Если на рисунке
тенденция строго не проявляется, то применяют более сложные
методы выявления тренда
Метод укрупнения интервалов - переход от первоначальных
значений динамического ряда к ряду с большими временными
промежутками. Так, месячные значения укрупняют в квартальные,
квартальные - в годовые, годовые - по пятилеткам и т.д. Возможно
простое суммирование величин, а также расчет средних уровней за
укрупненный период.
Метод скользящей средней - расчет средних уровней
динамического ряда по укрупненным интервалам путем
последовательного смещения начала отсчета на один временной
период, т.е. исключают из укрупненного интервала первые уровни
и включают последующие.
21.
Метод укрупнения интерваловy1
y2
y3
y4
y5
y6
y7
y8
…
…
yТ-2 yТ-1
Метод скользящей средней
y8 … yТ-2 yТ-1 yТ
…
…
…
… … … … … … … … … … … …
…
y1
y2
y3
y4
y5
y6
y7
yТ
22.
ФункцияЛинейная
Парабола
второго
порядка
Показательная
Гипербола
Формула
Рекомендации
используется в том случае, если
первые разности уровней
(абсолютные приросты) более
или менее постоянны
используется в том случае, если
вторые разности уровней
(ускорения) более или менее
постоянны
используется в том случае, если
цепные коэффициенты роста
примерно постоянны
используется в том случае, если
обнаружено замедленное
снижение (рост) уровней ряда,
которые по логике не могут
снизиться до нуля (превысить
какое-либо значение)
23.
Тренд в форме линейной функции- систему нормальных
уравнений
Моменты (периоды) времени
Моменты (периоды) времени
расстановлены от середины
расстановлены от начала ряда
ряда
24. Методы выявления и описания сезонной составляющей динамического ряда
25.
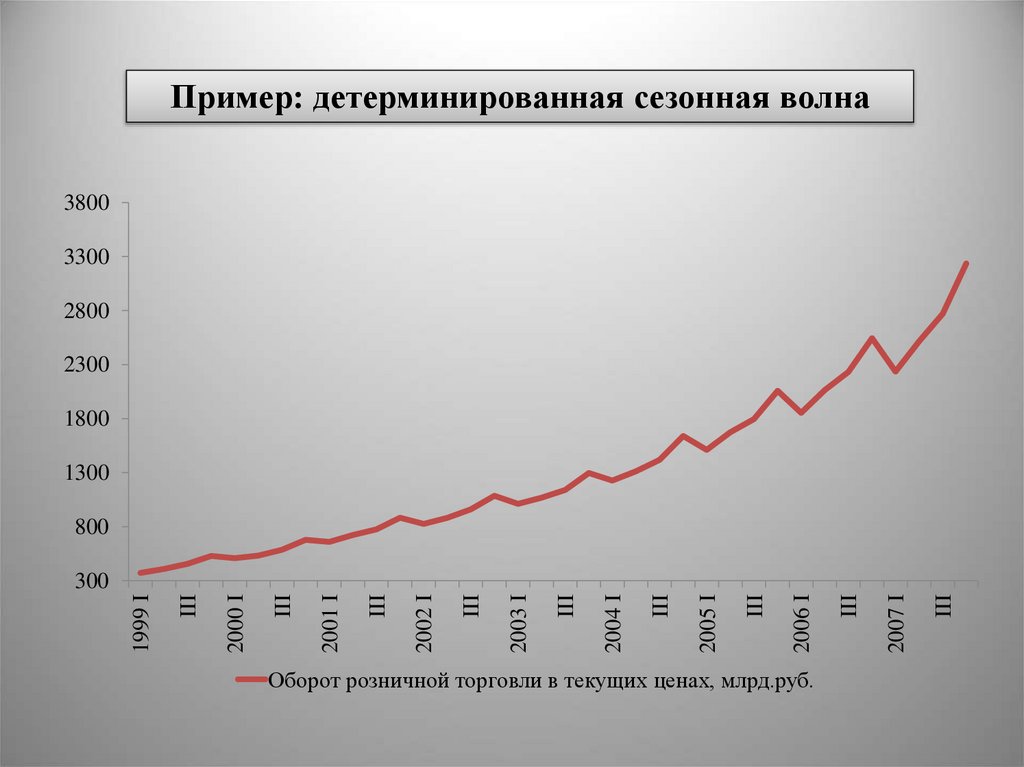
Виды сезонной составляющей временного рядадетерминированная
сезонная волна данный
тип встречается в
стабильно развивающихся
экономиках
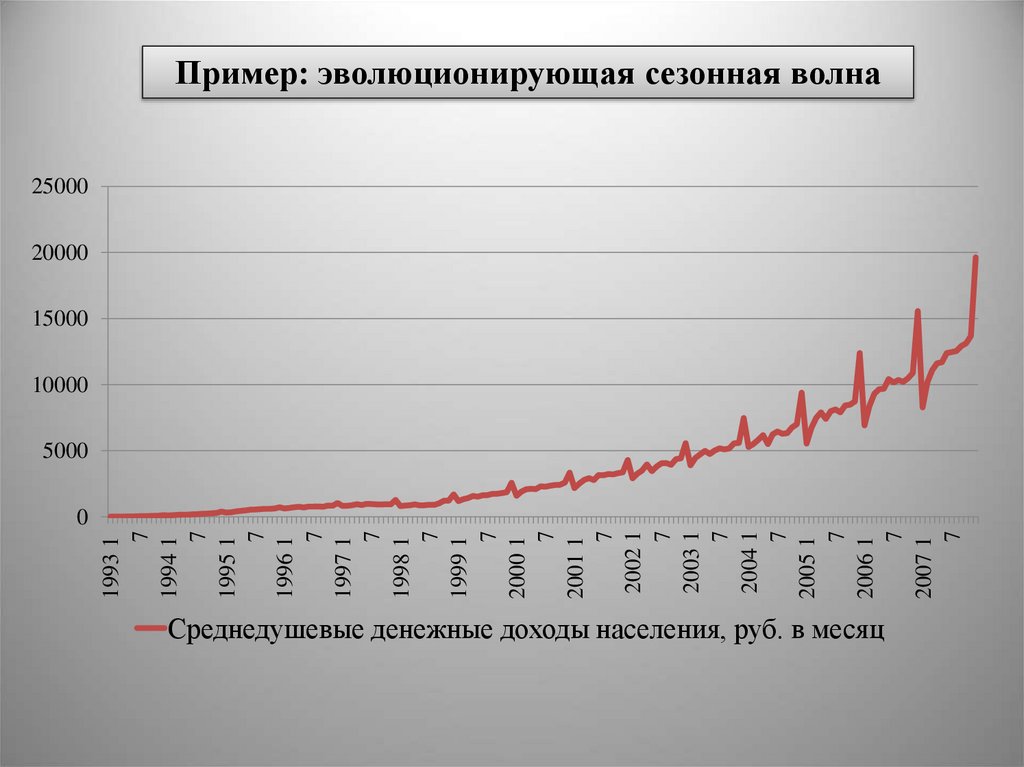
эволюционирующая
сезонная волна данный
тип характерен для
экономики переходного
периода
26.
Пример: детерминированная сезонная волна3800
3300
2800
2300
1800
1300
800
Оборот розничной торговли в текущих ценах, млрд.руб.
III
2007 I
III
2006 I
III
2005 I
III
2004 I
III
2003 I
III
2002 I
III
2001 I
III
2000 I
III
1999 I
300
27. Для выявления детерминированной сезонной волны используют такие методы как:
исчисление индексов сезонности;десезонализация данных;
сезонная декомпозиция временного ряда;
фиктивные переменные;
преобразование Фурье.
28.
На первом этапе расчет индекса сезонности строят таблицуКвартал 2004г. 2005г. 2006г.
1
2
3
4
Сумма
х
х
х
Индекс сезонности
Iсез
4
На втором этапе рассчитывается средний уровень
показателя по одноименным месяцам за ряд лет, для всех
12 месяцев (или 4 кварталов)
На третьем этапе рассчитывается
средняя за год по усредненным по
месяцам данным
На четвертом этапе рассчитываются
индексы сезонности
29.
Преобразование Фурьеm – число гармоник;
k – номер гармоники.
Параметры уравнения
30.
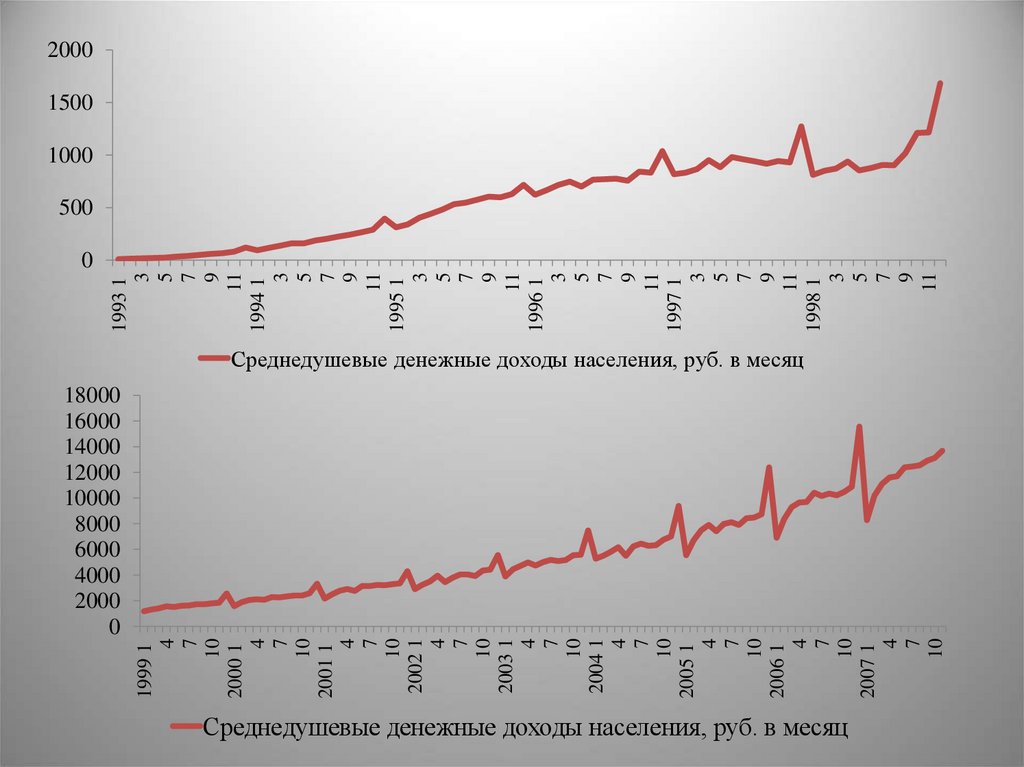
Пример: эволюционирующая сезонная волна25000
20000
15000
10000
5000
1993 1
7
1994 1
7
1995 1
7
1996 1
7
1997 1
7
1998 1
7
1999 1
7
2000 1
7
2001 1
7
2002 1
7
2003 1
7
2004 1
7
2005 1
7
2006 1
7
2007 1
7
0
Среднедушевые денежные доходы населения, руб. в месяц
31.
20001500
1000
0
1993 1
3
5
7
9
11
1994 1
3
5
7
9
11
1995 1
3
5
7
9
11
1996 1
3
5
7
9
11
1997 1
3
5
7
9
11
1998 1
3
5
7
9
11
500
18000
16000
14000
12000
10000
8000
6000
4000
2000
0
1999 1
4
7
10
2000 1
4
7
10
2001 1
4
7
10
2002 1
4
7
10
2003 1
4
7
10
2004 1
4
7
10
2005 1
4
7
10
2006 1
4
7
10
2007 1
4
7
10
Среднедушевые денежные доходы населения, руб. в месяц
Среднедушевые денежные доходы населения, руб. в месяц
32. Для выявления эволюционирующей сезонной волны используют такие методы как:
процедура X-12-ARIMA является расширенной версиейпроцедуры сезонной корректировке X-11 разработанной
Бюро переписей США.
процедура ES (Extract Seasons) методики заключается в
применении непараметрического алгоритма сезонной - суть
корректировки временных рядов основанному на
использовании вариационных принципов.
процедура TRAMO/SEATS. Данная процедура основывается
на ARIMA моделях, была разработана Maravall и Gomez и
реализована в программе Burman.
BV4 - метод сезонной корректировки основанный на
скользящем фильтре методом регрессии. В настоящее время
является официальным методом сезонной корректировки
Центрального Статистического Офиса Германии.
33. Методы измерения колеблемости и устойчивости уровней ряда
34.
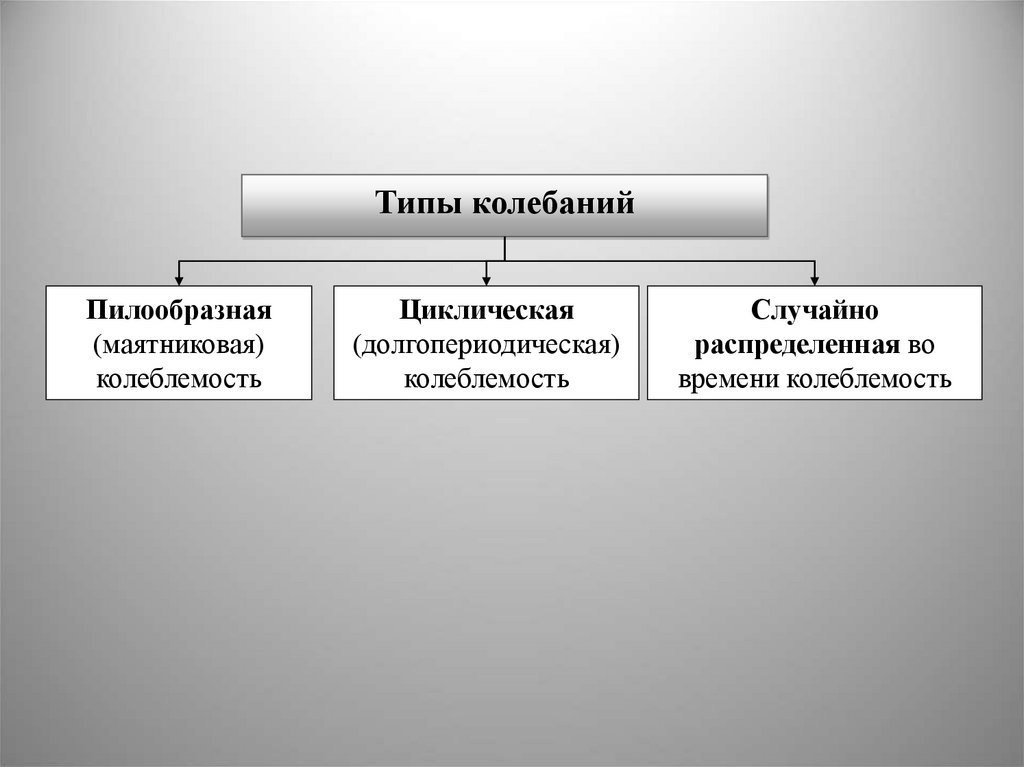
Типы колебанийПилообразная
(маятниковая)
колеблемость
Циклическая
(долгопериодическая)
колеблемость
Случайно
распределенная во
времени колеблемость
35.
Размах колеблемости средних уровнейИндексом устойчивости уровней
Чем ближе к единице показатель, тем меньше
колеблемость, а соответственно выше устойчивость
- средней уровней выше тренда;
- средней уровней ниже тренда.
36.
Среднее линейное отклонениеСреднее квадратичгеское отклонение
в случае генеральной совокупности
в случае выборочной совокупности
37.
Коэффициент колеблемостив случае
генеральной
совокупности
Vt
в случае
выборочной
совокупности
Интерпритация
(0; 0,1)
слабая колеблемость
[0,1; 0,2)
умеренная колеблемость
[0,2; 0,4)
сильная колеблемость
[0,4; 1]
сильная колеблемость
























 mathematics
mathematics








