Гз №2

1.

ДС-816
«Основы построения АСУ»
Раздел 1. Основы построения АСУ
Тема 1. Автоматизация управления сложными системами
Групповое занятие №2
«ТЕХНОЛОГИЯ ПРИНЯТИЯ РЕШЕНИЙ»
Тверь – 2025 г.

2.

Учебные и воспитательные цели
1. Усвоить состав и общую структуру задачи принятия решения, а также
возможные способы формализованного описания целей управления.
2. Вызвать интерес к информационным технологиям получения нового
информационного продукта – оптимального плана функционирования
ОУ либо план его перевода в состояние, отвечающее поставленным
целям.
3. Сформировать уровень обученности «Знать» фундаментальные категории
системологии в рамках формирования компетенции Способность к
логическому
мышлению,
обобщению,
анализу,
критическому
осмыслению,
систематизации,
прогнозированию,
постановке
исследовательских задач профессиональной деятельности и выбору
путей их решения.

3.

Учебные вопросы
1. Характеристика модели задачи принятия решений.
2. Способы формализованного описания целей управления.
Литература
• л.1/о – с.50:
Автоматизированные системы специального назначения. Часть 1.
Теоретические основы автоматизированного управления: Учебн.
пособ. – Тверь: ВА ВКО, 2021.
• л.1/Э
Автоматизированные системы специального назначения. Часть 1.
Теоретические основы автоматизированного управления
[Электронный ресурс]: учебное пособие. – Тверь: ВА ВКО, 2021.
.URL: http://ibook.academy.org/book/115

4.

Семинар №1
«ПРОБЛЕМЫ АВТОМАТИЗАЦИИ УПРАВЛЕНИЯ
СЛОЖНЫМИ СИСТЕМАМИ»
Учебные вопросы
1. Основные подсистемы АСУ и их характеристика.
2. Содержание процесса принятия решений в АСУ.

5.

Вопрос №1. Характеристика модели задачи принятия решений
Выработка и принятие решений осуществляется в процессе выполнения всех
задач управления - обязательный элемент технологии их выполнения.
Процесс управления - последовательность решения возникающих и повторяющихся
во времени задач управления.
Основные признаки задачи принятия решения:
1) у ЛПР должна быть определенная цель;
2) ЛПР должен обладать средствами влияния на результат.
Задача принятия решения может быть сформулирована в терминах:
-цель,
-средства (конкретные действия; определенные способы действий; планы;
программы …)
-результат.
Автоматизация
формальная (математическая) модель задачи
принятия решения (ММ ЗПР).
ММ ЗПР - формальное описание составляющих ее элементов:
- цель управления,
- управляющие воздействия (все возможные действия (АЛЬТЕРНАТИВЫ)),
- результаты управления (ИСХОДЫ),
- связи между воздействиями и результатами.
Трудность в принятии решений:
- формирование множества допустимых действий,
- формирование какого-то оригинального, необычного, нестандартного действия.

6.

Вопрос №1. Характеристика модели задачи принятия решений
Вариант задачи выбора (математической постановки) определяется
сочетанием следующих компонент:
+ множество альтернатив может быть конечным, счетным, континуальным;
+ оценка альтернатив осуществлена по одному или по нескольким
показателям, (количественным или качественным);
+ режим выбора может быть однократным (разовым) или повторяющимся,
допускающим обучение на опыте;
+ последствия выбора могут быть
-точно известны (выбор в условиях определенности),
-иметь вероятностный характер, когда известны вероятности возможных
исходов после сделанного выбора (выбор в условиях риска),
-иметь неоднозначный исход, не допускающий введения вероятностей
(выбор в условиях неопределенности);
+ответственность за выбор может быть индивидуальной (индивидуальное
ЛПР) или групповой (групповое ЛПР) индивидуальный и групповой выбор;
+степень согласованности целей при групповом выборе:
-полное совпадение интересов сторон (кооперативный выбор)
-противоположное совпадение интересов (выбор в конфликтной
ситуации).
Возможны многообразные задачи выбора!

7.

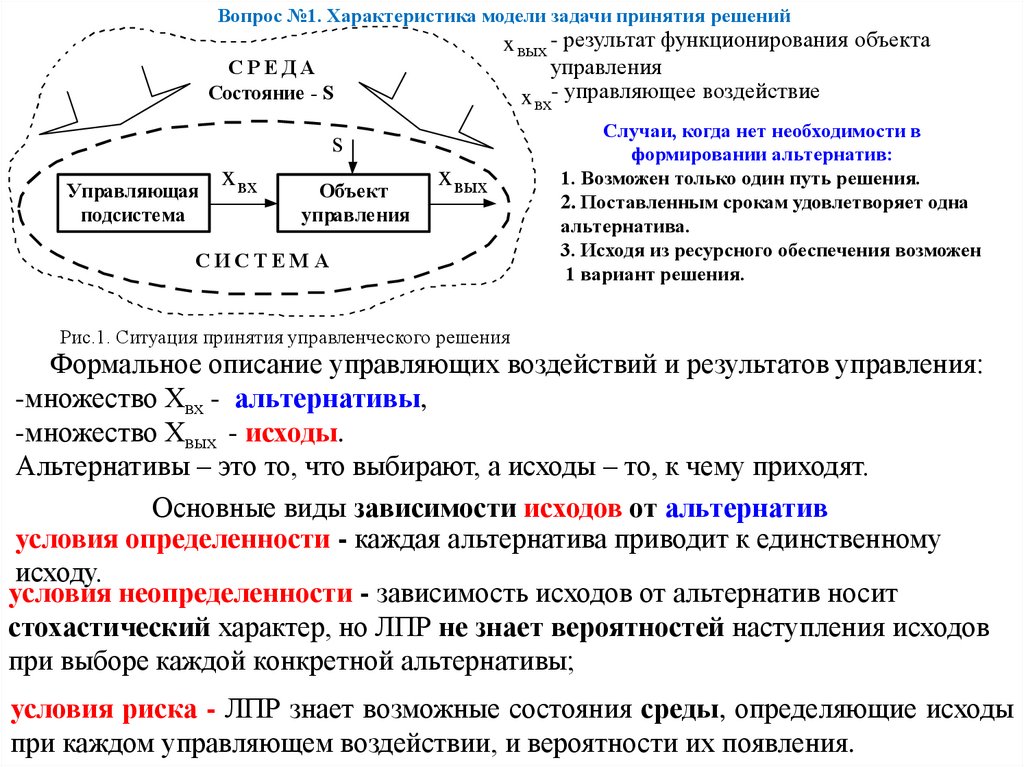
Вопрос №1. Характеристика модели задачи принятия решений
x вых - результат функционирования объекта
управления
x вх- управляющее воздействие
СРЕДА
Состояние - S
s
Управляющая
подсистема
x вх
Объект
управления
x вых
СИСТЕМ А
Случаи, когда нет необходимости в
формировании альтернатив:
1. Возможен только один путь решения.
2. Поставленным срокам удовлетворяет одна
альтернатива.
3. Исходя из ресурсного обеспечения возможен
1 вариант решения.
Рис.1. Ситуация принятия управленческого решения
Формальное описание управляющих воздействий и результатов управления:
-множество Хвх - альтернативы,
-множество Хвых - исходы.
Альтернативы – это то, что выбирают, а исходы – то, к чему приходят.
Основные виды зависимости исходов от альтернатив
условия определенности - каждая альтернатива приводит к единственному
исходу.
условия неопределенности - зависимость исходов от альтернатив носит
стохастический характер, но ЛПР не знает вероятностей наступления исходов
при выборе каждой конкретной альтернативы;
условия риска - ЛПР знает возможные состояния среды, определяющие исходы
при каждом управляющем воздействии, и вероятности их появления.

8.

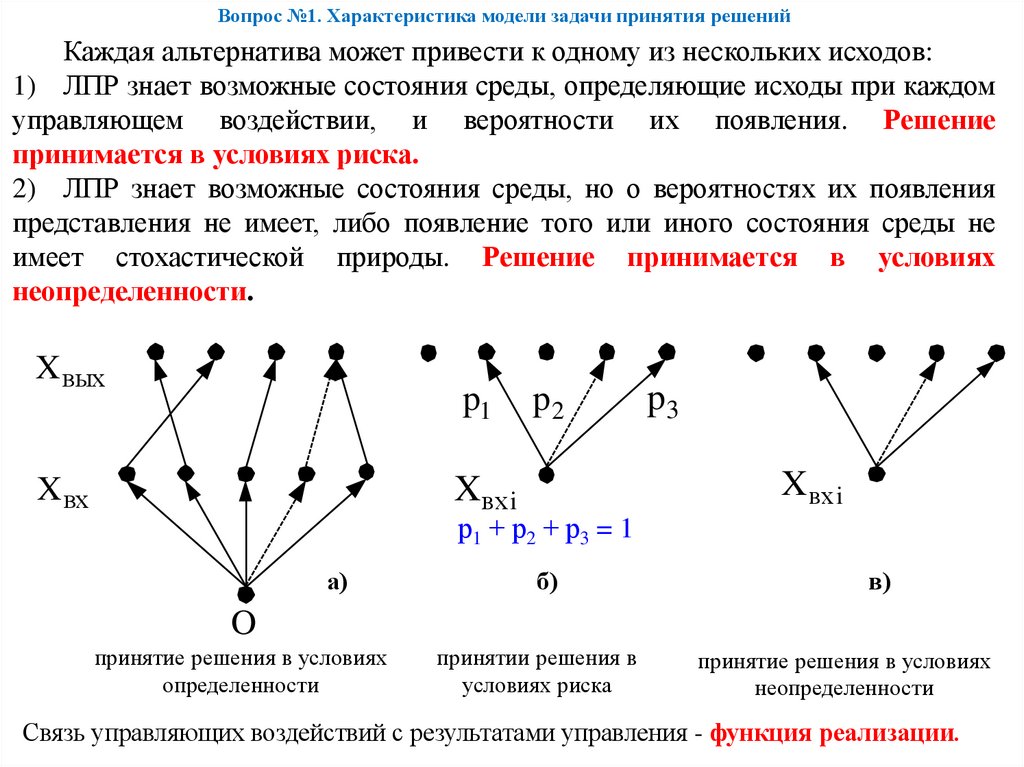
Вопрос №1. Характеристика модели задачи принятия решений
Каждая альтернатива может привести к одному из нескольких исходов:
1) ЛПР знает возможные состояния среды, определяющие исходы при каждом
управляющем воздействии, и вероятности их появления. Решение
принимается в условиях риска.
2) ЛПР знает возможные состояния среды, но о вероятностях их появления
представления не имеет, либо появление того или иного состояния среды не
имеет стохастической природы. Решение принимается в условиях
неопределенности.
X вых
p1
p2
X вх i
Xвх i
X вх
p3
р1 + р2 + р3 = 1
а)
б)
в)
O
принятие решения в условиях
определенности
принятии решения в
условиях риска
принятие решения в условиях
неопределенности
Связь управляющих воздействий с результатами управления - функция реализации.

9.

Вопрос №1. Характеристика модели задачи принятия решений
Задача принятия решения по управлению объектом
(в рамках системного описания )
Пусть X вх xвх1 , xвх 2 , , xвх i , , xвх m
S s1 , , s j , , sn
- множество всех альтернатив
– множество всех состояний среды
X вых xвых1 , xвых 2 , , xвых k , , xвых r – множество возможных исходов
Каждый исход
xвых ψ xвх ,s , где xвх X вх , s S
- функция реализации - сопоставляет каждой паре «альтернатива –
состояние среды» определяемый ею исход.
Если множество альтернатив и множество состояний среды конечны, то
Функция реализации в условиях неопределенности

10.

Вопрос №1. Характеристика модели задачи принятия решений
Функция реализации в условиях риска
Функция реализации может быть задана аналитически (очень редко).
На практике - функция реализации задается алгоритмически
моделирующим алгоритмом, имитирующим процессы, протекающие
- в ОУ,
- окружающей среде,
- у противника,
- в результате боевых действий.
Задачу принятия решения, когда связь управляющих воздействий с
результатами управления представлена функцией реализации, называют
задачей принятия решения в форме функции реализации.
–

11.

Вопрос №2. Способы формализованного описания целей управления
Возможные способы формализованного описания целей
Цели должны быть измеримыми: либо количественно, либо качественно.
Описание цели – это создание её (цели) модели.
Интегральная оценка эффективности (качества) решения - предпочтение - мера
степени достижения цели управления при реализации выбранного управляющего
воздействия.
Предпочтение задается функцией предпочтения :
f f xвх
Функция предпочтения: f xвых ij f xвх i , s j f ij - оценка решения xвх i
с точки зрения обеспечения степени достижения цели управления в ситуации s j , или
предпочтительность результата управления (исхода xвых ij ) по отношению к цели
управления.
Если множество альтернатив и множество состояний среды конечны

12.

Вопрос №2. Способы формализованного описания целей управления
Если предпочтение измерено количественно, то модель цели - показатель степени
достижения цели или целевая функция
k k xвх
Принцип оптимальности: Наилучшее решение по управлению соответствует
максимальному (минимальному) значению показателя (целевой функции).
Модель задачи выбора оптимального управления
o
xвх
arg max k xвх
k x вх max
x вх X вх
x вх X вх
для условий определенности:
-состояние среды достоверно известно;
-каждой альтернативе соответствует один исход, - функция предпочтения и целевая
функция не зависят от s, т. е.:
k x вх f x вх max
x вх X вх
o
xвх
arg max f xвх
x вх X вх

13.

Вопрос №2. Способы формализованного описания целей управления
Для условий неопределенности возможны стратегии ЛПР:
1) пессимистическая, 2) оптимистическая, 3) рациональная.
избегает риска и рассчитывает на
минимальный гарантируемый результат
Пессимистическая стратегия - критерия пессимизма
s S
o
xвх
arg max min f xвх , s
k x вх min f x вх , s max
s S
k x вх min f x вх , s
x вх X вх s S
x вх X вх
Функция предпочтения
–
s1
s2
s3
k ( xвх )
xв х1
1
2
1
2
xвх 2
2
1
3
3
xвх 3
3
3
2
3
Критерий выбора – k( xвхi ) max fij
j
o
k ( xвх i )
Правило выбора –xвх arg min
i
По критерию пессимизма оптимальным является решение
xвх 1

14.

Вопрос №2. Способы формализованного описания целей управления
Для условий неопределенности возможны стратегии ЛПР:
2) оптимистическая
надеется на максимальный результат
Оптимистическая стратегия - критерий оптимизма
s S
k x вх max f xвх , s max
s S
k x вх max f x вх , s
o
xвх
arg max max f xвх , s
x вх X вх
x вх X вх s S
Функция предпочтения
–
s1
s2
s3
k ( xвх )
xвх 1
1
2
1
1
xвх 2
2
1
3
1
xвх 3
3
3
2
2
Критерий выбора – k ( xвх i ) min f ij Правило выбора – x o arg min k ( x )
вх
вх i
j
По критерию оптимизма оптимальными являются два решения:
Причем решение
i
х вх 1
хвх 2
х вх 1 является оптимальным и по критерию пессимизма.

15.

Вопрос №2. Способы формализованного описания целей управления
Для условий неопределенности возможны стратегии ЛПР: 3) рациональная.
Рациональная стратегия - критерий пессимизма-оптимизма (Гурвица)
h = 0 - критерий оптимизма
k x h min f x , s 1 h max f x , s
вх
вх
s S
вх
s S
k x вх h min f x вх , s 1 h max f x вх , s
s S
x oвх arg
s S
h
min
f
x
,
s
1
h
max
f
x
,
s
вх
вх
x вх X вх s S
s S
Функция предпочтения
s1
s2
s3
s4
xвх 1
1
3
4
4
8
6
5
4
6
9
3
2
xвх 3
x вх X вх
max
–
xвх 2
max
k ( xвх ) при h = 0,4
j
j
Изменяющийся в пределах
0 h 1
k ( xвх ) при h = 0,3
5,8
6,0
4,4
Критерий выбора – k ( xвх i ) h min fij (1 h) max fij
h = 1 - критерий пессимизма
6,6
6,5
4,8
o
Правило выбора –xвх arg max k ( xвх i )
i
Пусть ЛПР на 40 % считает свою стратегию пессимистической и на 60 %
оптимистической. Это означает, что h = 0,4,
Для этого случая оптимальным является решение xвх 2
Если h = 0,3, то оптимальным становится решение xвх 1
.

16.

Вопрос №2. Способы формализованного описания целей управления
Для условий риска (известны вероятности возникновения ситуаций) - рациональная
стратегия.
«Рациональный» критерий - «среднее предпочтение» – математическое ожидание функции
предпочтения на множестве возможных исходов
n
k x вх p j f x вх , s j
j 1
n
k x вх p j f x вх , s j max
j 1
x вх Xвх
Функция предпочтения
–
s1
s2
s3
s4
k ( xвх )
xвх 1
1
3
4
0,1
4
8
6
0,2
5
4
6
0,5
9
3
2
0,2
5,2
4,5
5,0
–
xв х 2
xвх 3
pj
По критерию максимума среднего выигрыша оптимальным является решение
xвх 1

17. Задание на самостоятельную работу

Изучить материалы, используя рекомендованную
литературу:
• л.1/о – с.50:
Автоматизированные системы специального назначения. Часть 1.
Теоретические основы автоматизированного управления: Учебн.
пособ. – Тверь: ВА ВКО, 2021.
• л.1/Э
Автоматизированные системы специального назначения. Часть 1.
Теоретические основы автоматизированного управления
[Электронный ресурс]: учебное пособие. – Тверь: ВА ВКО, 2021.
URL: http://ibook.academy.org/book/115.

18.

Семинар №1
«ПРОБЛЕМЫ АВТОМАТИЗАЦИИ УПРАВЛЕНИЯ
СЛОЖНЫМИ СИСТЕМАМИ»
Учебные вопросы
1. Основные подсистемы АСУ и их характеристика.
2. Содержание процесса принятия решений в АСУ.

19.

Вопрос №2. Способы формализованного описания целей управления
Для условий неопределенности возможны стратегии ЛПР:
1) пессимистическая, 2) оптимистическая, 3) рациональная.
избегает риска и рассчитывает на
минимальный гарантируемый результат
надеется на максимальный
результат
k x вх min f x вх , s
Пессимистическая стратегия - критерия пессимизма
o
xвх
arg max min f xвх , s
k x вх min f x вх , s max
s S
x вх X вх s S
x вх X вх
Оптимистическая стратегия - критерий оптимизма
k x вх max f xвх , s max
s S
x вх X вх
s S
k x вх max f x вх , s
s S
o
xвх
arg max max f xвх , s
x вх X вх s S
Рациональная стратегия - критерий пессимизма-оптимизма (Гурвица)
k x вх h min f x вх , s 1 h max f x вх , s
s S
s S
k x вх h min f x вх , s 1 h max f x вх , s
s S
x oвх arg
h = 0 - критерий оптимизма
s S
max
x вх X вх
h
min
f
x
,
s
1
h
max
f
x
,
s
вх
вх
x вх X вх s S
s S
max