Презентация к уроку алгебры %22Сравнение значений вы

1.

Алгебра – 7
Сравнение значений
выражений
Материал к уроку

2.

Повторение
Укажите допустимые
значения переменных для выражения:
I
2х − 7 у + 2
(х + 3)( у − 2)
Ответ
II
у − 2 0, у 2
х и у – любые числа, кроме х = – 3 и у = 2
3х − 4 у − 1
(х − 5)( у + 3)
Ответ
х + 3 0, х −3
х − 5 0, х 5
у + 3 0, у −3
х и у – любые числа, кроме х = 5 и у = – 3

3.

Повторение
Напишите формула числа, которое …
…при делении на 6 даёт остаток 4.
I
т = 6 п + 4
Проверка
…при делении на 8 даёт остаток 5.
II
т = 8 п + 5
Проверка

4.

Сравнение значений выражений
1. Сравнение значений выражений
2. Числовые неравенства

5.

1. Сравнение значений выражений
Пример 1
Сравним значения числовых выражений:
(3 − 4): 5 и (2 + 6): 8
2
2
Решение (6)
(3 − 4): 5 = (9 − 4) : 5 = 5 : 5 = 1
2)
(2 + 6): 8 = (4 + 6) : 8 = 10 : 8 = 1,25
3)
1 1,25 или (3 − 4 ) : 5 (2 + 6 ) : 8
1)
2
2
2
2

6.

1. Сравнение значений выражений
Пример 2
1)
Сравните значения числовых выражений,
не вычисляя их:
<
=
9 : 0,6 <
и 9 0,6
2,1 − 1,8 >
и 2,1 − 5,2
6,16 − 7,44 <
и 7,44 − 6,16
2
7
56 и= 56 :
7
2
>

7.

1. Сравнение значений выражений
Пример 2
2)
Сравните значения числовых выражений,
не вычисляя их:
<
=
6,13 − 7,57 <
и − 6,13 + 7,57
5,7 − 3,33 <
и 5,7 − 3,22
24,12 0,4 и
> 24,12 : 0,4
5
1
65,4 и= 65,4 : 1
6
5
>

8.

1. Сравнение значений выражений.
При сравнении значений алгебраических
выражений при разных значениях переменных
результат может оказаться как различным,
так и одинаковым
Сравним 2 · а – 3 и 6 – а при а = 1, 3:
2а − 3 = −1 и 6 − а = 5
тогда 2а − 3 6 − a
2) Если а = 3, то
2а − 3 = 3 и 6 − а = 3
тогда 2а − 3 = 6 − a
1) Если а = 1, то

9.

1. Сравнение значений выражений
Пример 3 Сравнить значения алгебраических выражений:
а + 5 и 4а + 1 при а = 3
2
Решение (6)
1)
а + 5 = 3 + 5 = 9 + 5 = 14
2)
4а + 1 = 4 3 + 1 = 12 + 1 = 13
3)
14 13 или а + 5 4а + 1
2
2
2

10.

1. Сравнение значений выражений
Пример 4 Сравнить значения алгебраических выражений:
4а + 2 и а − 2 при а = 5
2
Решение (6)
1)
4а + 2 = 4 5 + 5 = 20 + 2 = 22
2)
а − 2 = 5 − 2 = 25 − 2 = 23
3)
22 23 или 4а + 2 а − 2
2
2
2

11.

1. Сравнение значений выражений
Пример 5 Сравнить значения алгебраических выражений:
(a − 2) и а − 4a + 4 при а = 0
2
2
Решение (6)
1)
(а − 2) = (0 − 2) = (− 2) = 4
2)
а − 4a + 4 = 0 − 4 0 + 4 = 4
3)
4 = 4 или (а − 2 ) = а − 4a + 4
2
2
2
2
2
2
2

12.

1. Сравнение значений выражений
Сравнить значения
Пример 6
алгебраических выражений:
<
=
>
I
II
=
<
при а = 3,8
при а = – 5
при а = – 5
при х = 1,6
9,5 − а >
и 0,5а
а и> 100а
при х = – 1
5 x − 0,8 =
и 0,8 x − 5
>
0,7a <
и 7,3 + 2,1a
3− х =
и 4х − 5
при х = – 1
−х >
и х

13.

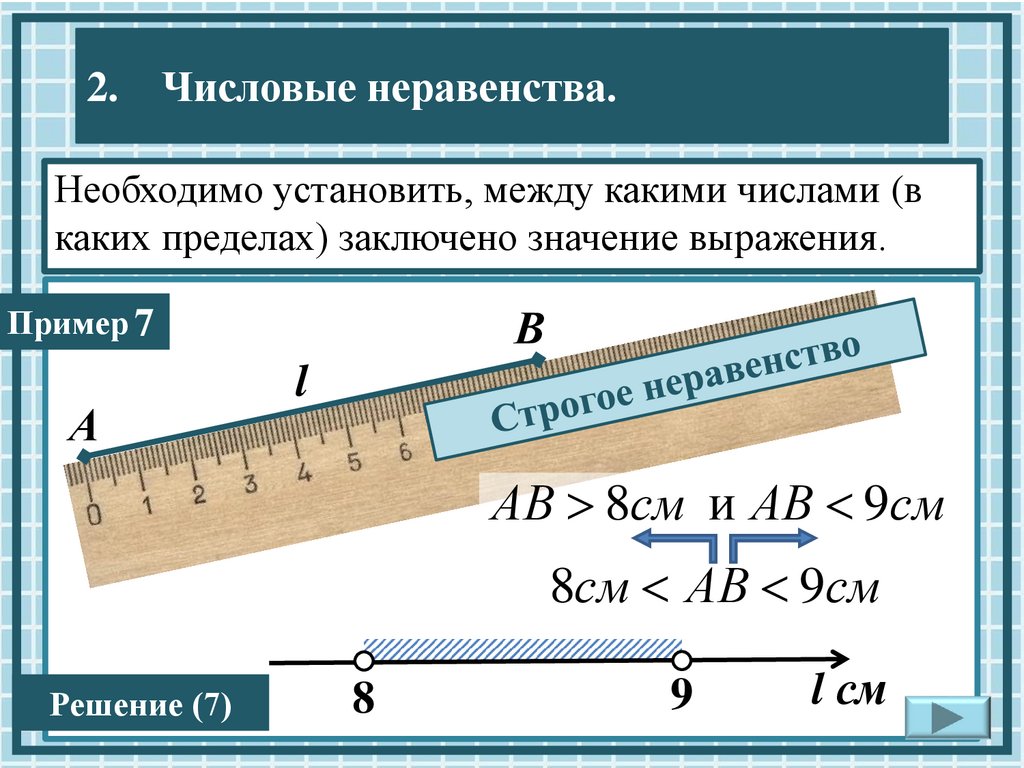
2.
Числовые неравенства.
Необходимо
установить, между какими числами (в
7
каких пределах) заключено значение выражения.
В
Пример 7
А
l
АВ 8см и АВ 9см
8см АВ 9см
Решение (7)
8
9
l см

14.

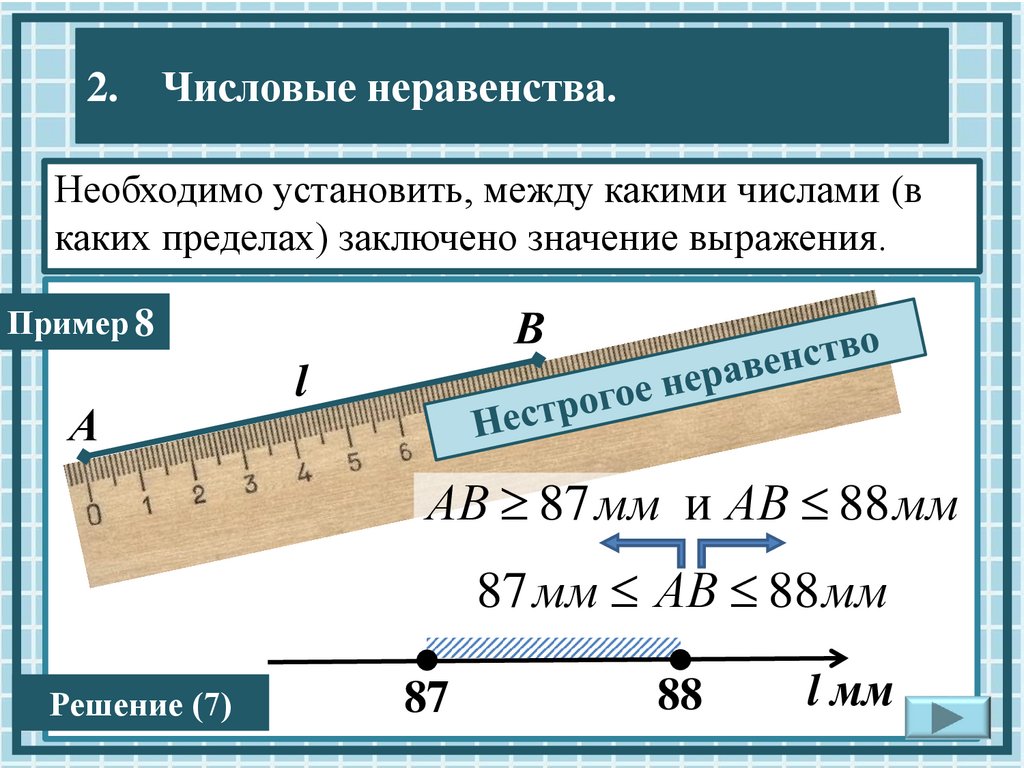
2.
Числовые неравенства.
Необходимо
установить, между какими числами (в
7
каких пределах) заключено значение выражения.
В
Пример 8
А
l
АВ 87 мм и АВ 88 мм
87 мм АВ 88 мм
Решение (7)
87
88
l мм

15.

2.
Числовые неравенства.
Пример 9
Запишите в виде двойного неравенства:
1)
8 меньше 13 и 13 меньше 15
8 13 15
2)
53,5 больше 53 и меньше 54
53 53,5 54
3)
– 8,1 больше –11 и меньше –7
− 11 −8,1 −7
4)
т больше –16 и меньше –15
− 16 т −15
5)
а больше х и меньше у
х а у

16.

2.
Числовые неравенства.
Пример 10
Запишите
двойного
неравенства:
Запишите вс виде
помощью
знаков
неравенства:
1)
х меньше или равно 8
8 х
2)
у больше или равно 0
у 0
3)
а больше 5 и меньше или равно 6
5 а 6
4)
т больше или равно –2 и меньше 1
− 2 т 1

17.

2.
Числовые неравенства.
Пример10
Запишите
неравенства:
Запишите вв виде
виде двойного
неравенства:
1)
х – отрицательное число
х 0
2)
п – положительное число
п 0
3)
у – неотрицательное число
у 0
4)
т – неположительное число
т 0