Similar presentations:
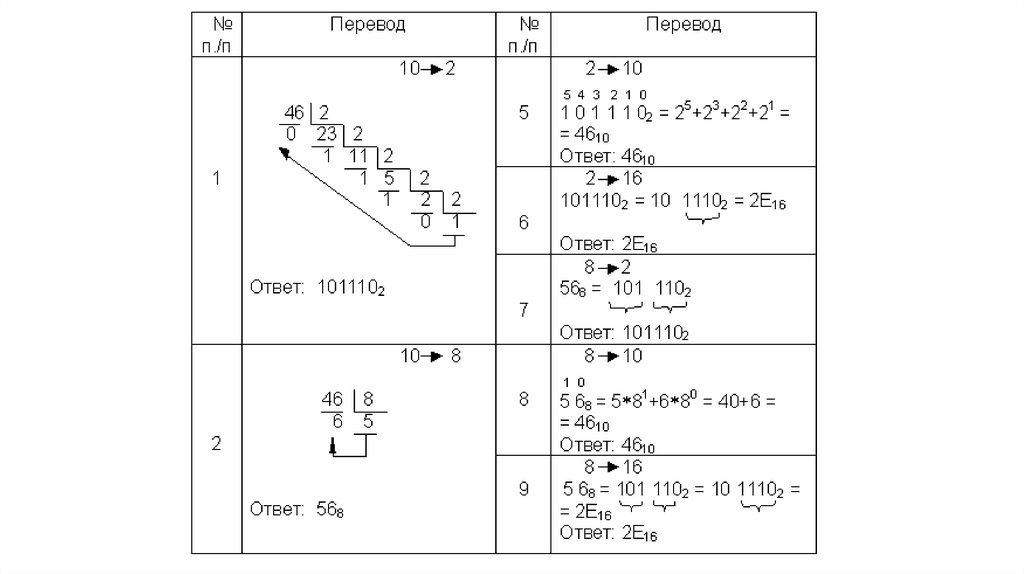
Перевод целых десятичных чисел в двоичную систему счисления
1.
2.
Бит - разряд памяти, который может приниматьдва значения: включено или выключено (1/0).
Байт — ячейка памяти состоящая из 8 бит.
Длина двоичного кода равняется количеству бит,
которое занимает код
Например, двоичный код буквы A - 01100001. Длина
двоичного кода – 8 двоичных цифр, следовательно данный код
занимает 8 бит.
3.
4.
5.
Перевести:1) 129 бит в байты =
6.
Перевести:1) 129 бит в байты =
15
7.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
8.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
960
9.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
960
3) 4096 байт в Кбайты =
10.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
960
3) 4096 байт в Кбайты =
4
11.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
960
3) 4096 байт в Кбайты =
4) 1 Кбайт в биты =
4
12.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
960
3) 4096 байт в Кбайты =
4) 1 Кбайт в биты = 8192
5) 2048 Кбайт в Мбайты =
4
13.
Перевести:1) 129 бит в байты =
2) 120 байт в биты =
15
960
3) 4096 байт в Кбайты =
4
4) 1 Кбайт в биты = 8192
5) 2048 Кбайт в Мбайты =
2
14.
Условие Фано: для того, чтобы сообщение,записанное с помощью неравномерного кода,
однозначно декодировалось, достаточно, чтобы
никакое кодовое слово не являлось началом
другого кодового слова.
15.
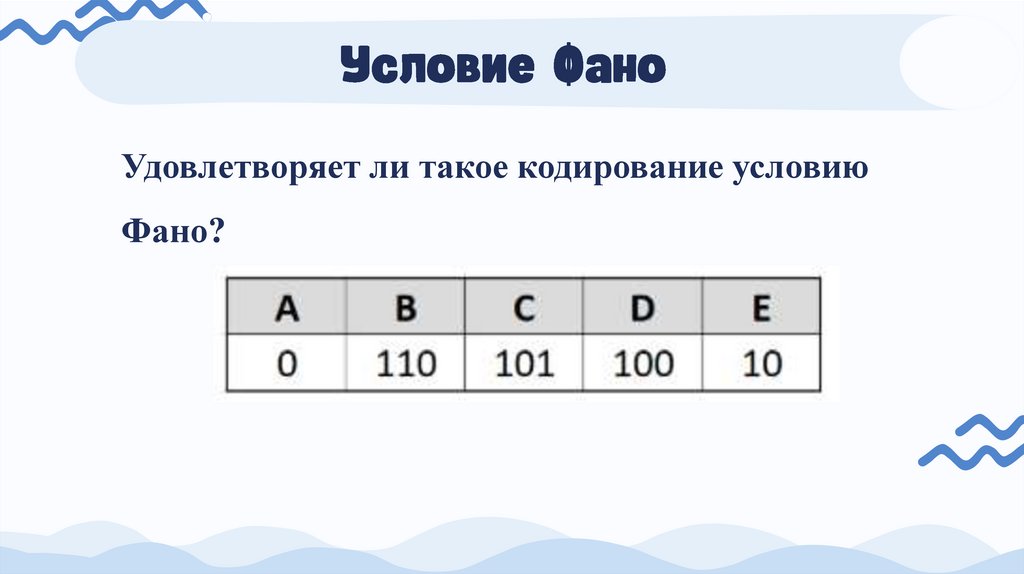
Удовлетворяет ли такое кодирование условиюФано?
16.
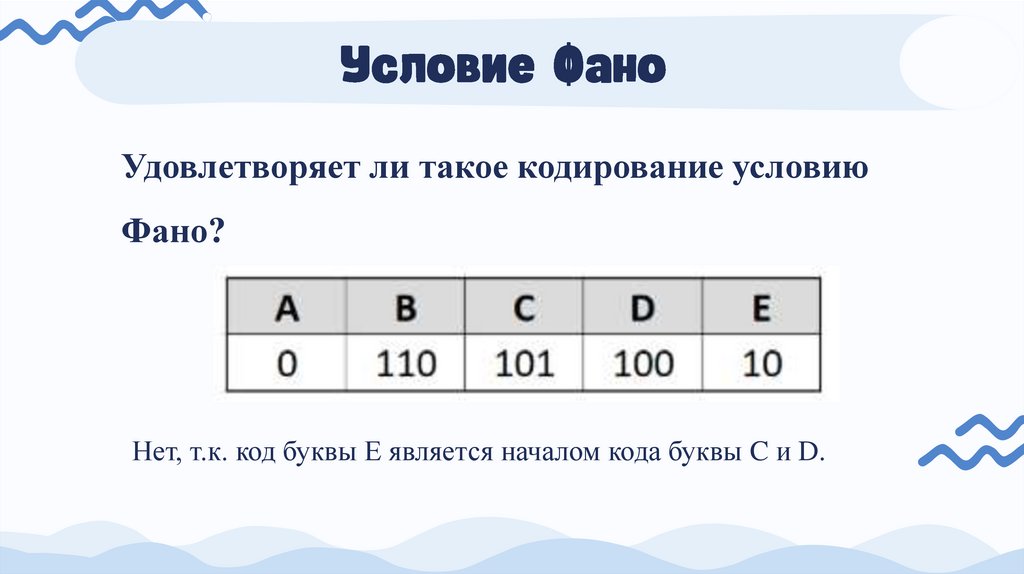
Удовлетворяет ли такое кодирование условиюФано?
Нет, т.к. код буквы Е является началом кода буквы C и D.
17.
Обратное условие Фано: для того, чтобысообщение, записанное с помощью
неравномерного кода, однозначно
декодировалось, достаточно, чтобы никакое
кодовое слово не являлось концом другого
кодового слова.
18.
Удовлетворяет ли такое кодированиеобратному условию Фано?
Удовлетворяет, так как никакое кодовое слово не
является концом другого кодового слова.
19.
Удовлетворяет ли такое кодированиеобратному условию Фано?
Не удовлетворяет, так как код буквы Е является
концом кода буквы B.
20.
Система счисления – это способ записи(представления) чисел.
Системы счисления делятся на позиционные и
непозиционные.
21.
ПозиционныеНепозиционные
Значение цифры зависит
от ее позиции
Значение цифры не
зависит от ее позиции
22.
ПозиционныеНепозиционные
Значение цифры зависит
от ее позиции
Значение цифры не
зависит от ее позиции
323
Три сотни
XIX
Три
единицы
десять
десять
23.
Алфавит системы счисления — это набор символов(цифр) для записи чисел.
Основание системы счисления — количество цифр
в алфавите.
24.
Алфавит системы счисления — это набор символов(цифр) для записи чисел.
Основание системы счисления — количество цифр
в алфавите.
Например,
• Алфавит 10-й системы счисления – {0,1,2,3,4,5,6,7,8,9}. Всего 10
цифр, следовательно, основание 10.
• Алфавит двоичной системы счисления – {0,1}. Основание 2.



































 informatics
informatics








