Similar presentations:
Криптография. Математика для систем с открытым ключом
1.
КриптографияМатематика для систем
с открытым ключом
Южный федеральный университет,
Ростов-на-Дону, 2019
sfedu.ru
2.
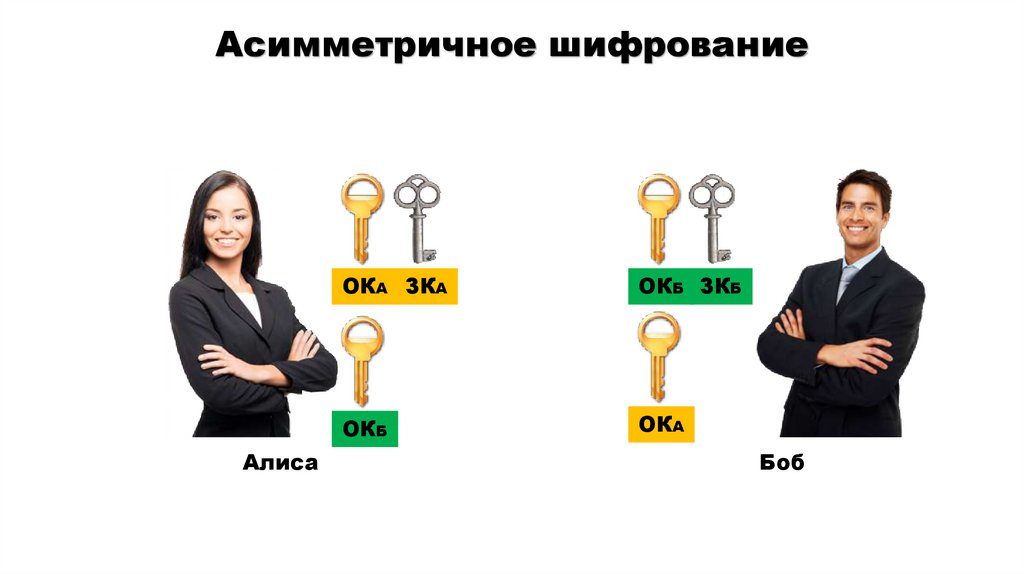
Асимметричное шифрованиеАлиса
ОКА ЗКА
ОКБ ЗКБ
ОКБ
ОКА
Боб
3.
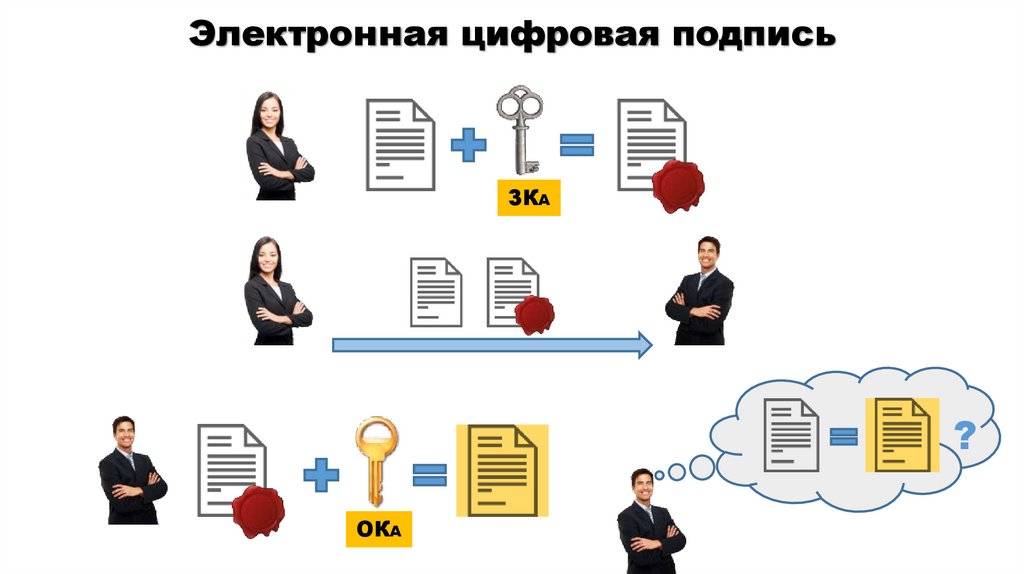
Электронная цифровая подписьЗКА
?
ОКА
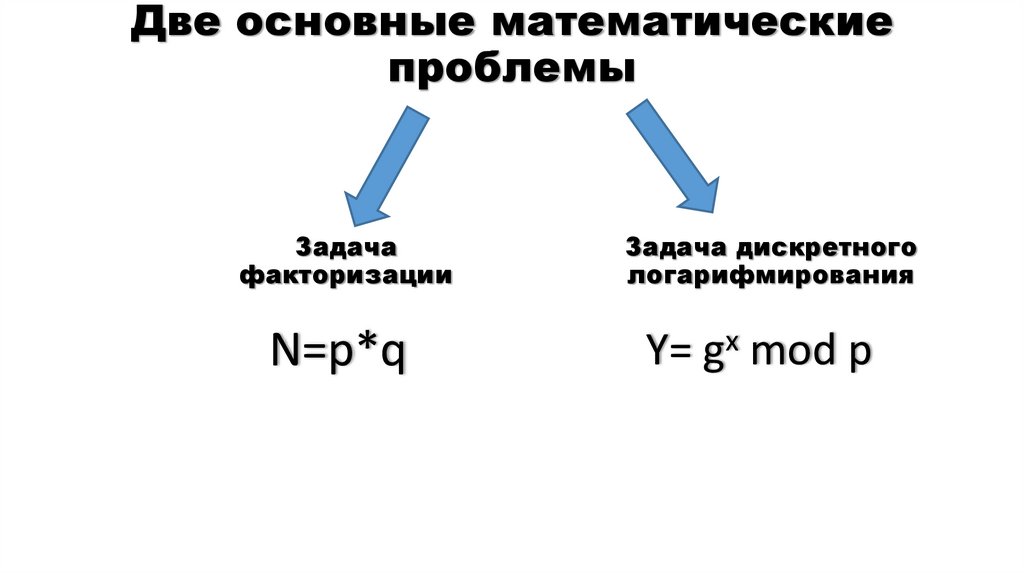
4. Две основные математические проблемы
Задачафакторизации
Задача дискретного
логарифмирования
N=p*q
Y= gx mod p
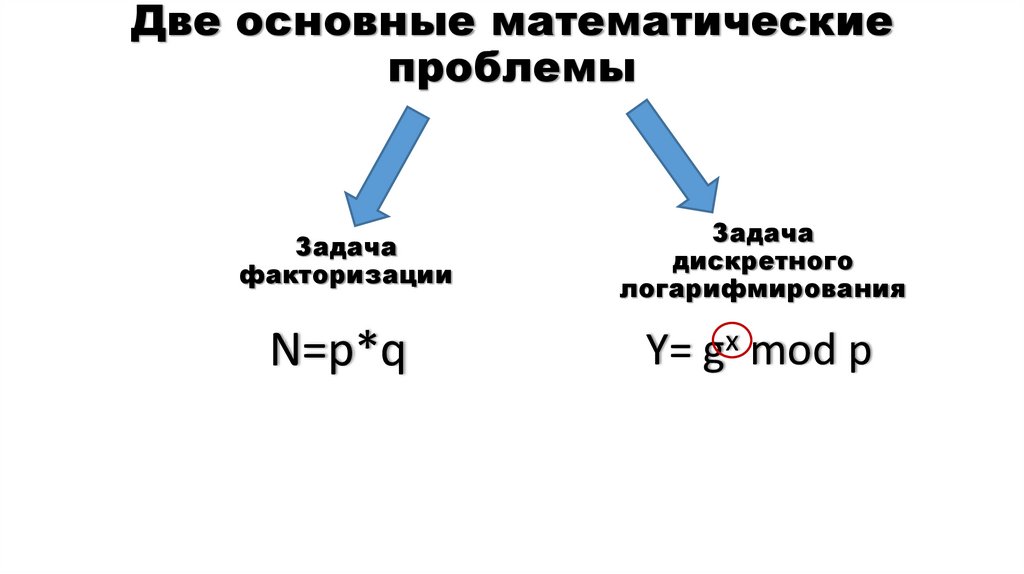
5. Две основные математические проблемы
Задачафакторизации
Задача
дискретного
логарифмирования
N=p*q
Y= gx mod p
6. Первообразный корень
Y= gx mod pр = 11
11 mod 11 = 1
12 mod 11 = 1
13 mod 11 = 1
21 mod 11 = 2
22 mod 11 = 4
23 mod 11 = 8
24 mod 11 = 5
25 mod 11 = 10
26 mod 11 = 9
27 mod 11 = 7
28 mod 11 = 3
29 mod 11 = 6
210 mod 11 = 1
51 mod 11 = 5 101 mod 11 = 10
52 mod 11 = 3 102 mod 11 = 1
53 mod 11 = 4
54 mod 11 = 9
55 mod 11 = 1
56 mod 11 = 5
211 mod 11 = 210 *2mod 11 = 2
7. Первообразный корень
Y= gx mod pp-1
1) g mod p = 1
m
2) g mod p ≠ 1 для всех m от 1 до p-2
Обычно проверяют только те степени,
которые являются делителем p-1
8. Первообразный корень
Y= gx mod p р = 11, g = 5gp-1 mod p = 510 mod 11 = (25)5 mod 11 =
(3)5 mod 11 = 81*3 mod 11 = 12 mod 11 = 1
9. Первообразный корень
Y= gx mod p р = 11, g = 5gp-1 mod p = 510 mod 11 = (25)5 mod 11 =
(3)5 mod 11 = 81*3 mod 11 = 12 mod 11 = 1
2) gmmod p ≠ 1 для всех m от 1 до p-2
Обычно проверяют только те степени,
которые являются делителем p-1
10. Первообразный корень
Y= gx mod p р = 11, g = 52) gmmod p ≠ 1 для всех m от 1 до p-2
Делители р-1: 1, 2, 5, 10
51 mod 11 = 5
52 mod 11 = 3
55 mod 11 = 1
11. Протокол Диффи - Хеллмана
Whitfield Diffie, Martin HellmanОпубликовано в 1976
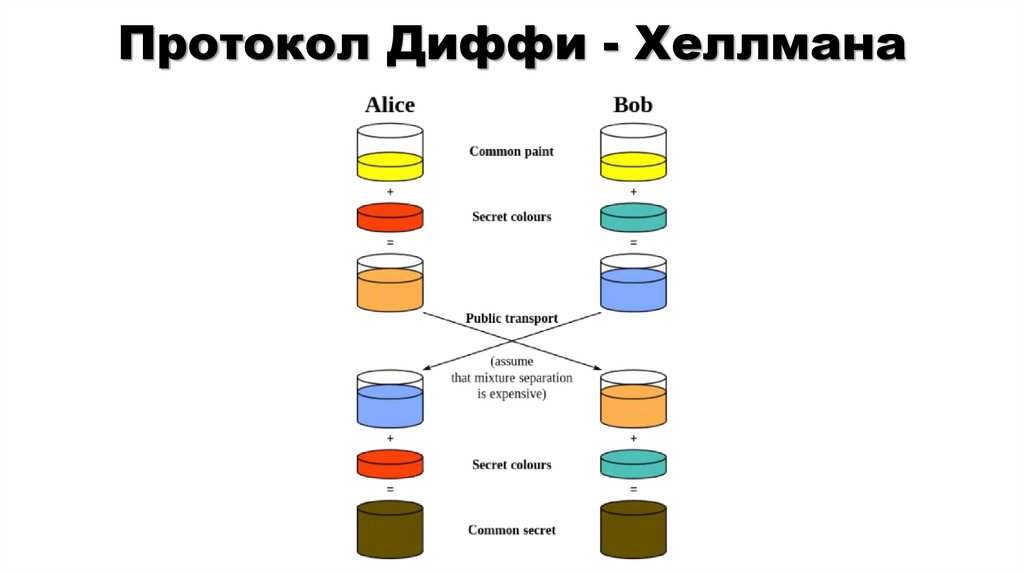
12. Протокол Диффи - Хеллмана
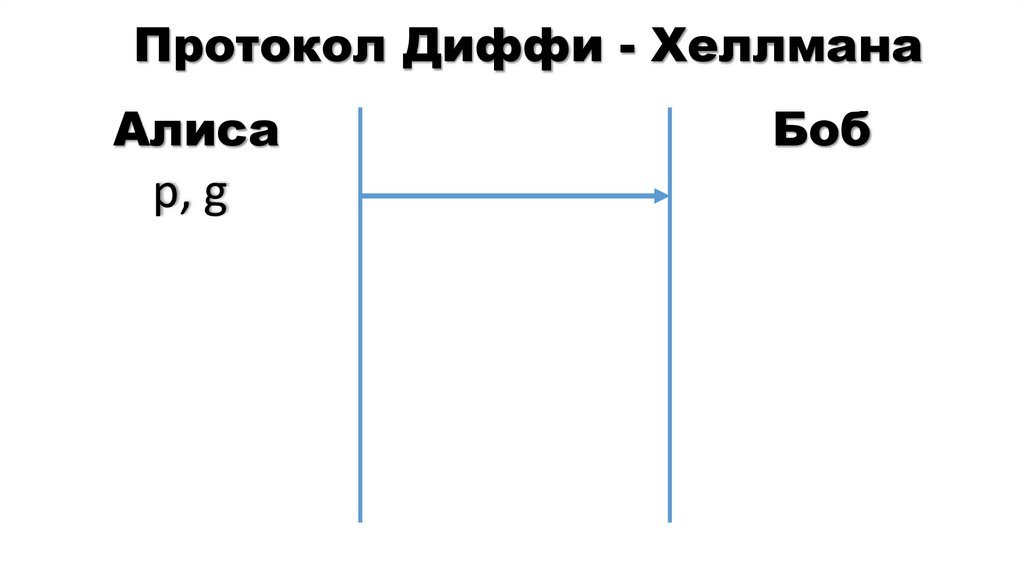
13. Протокол Диффи - Хеллмана
Алисар, g
Боб
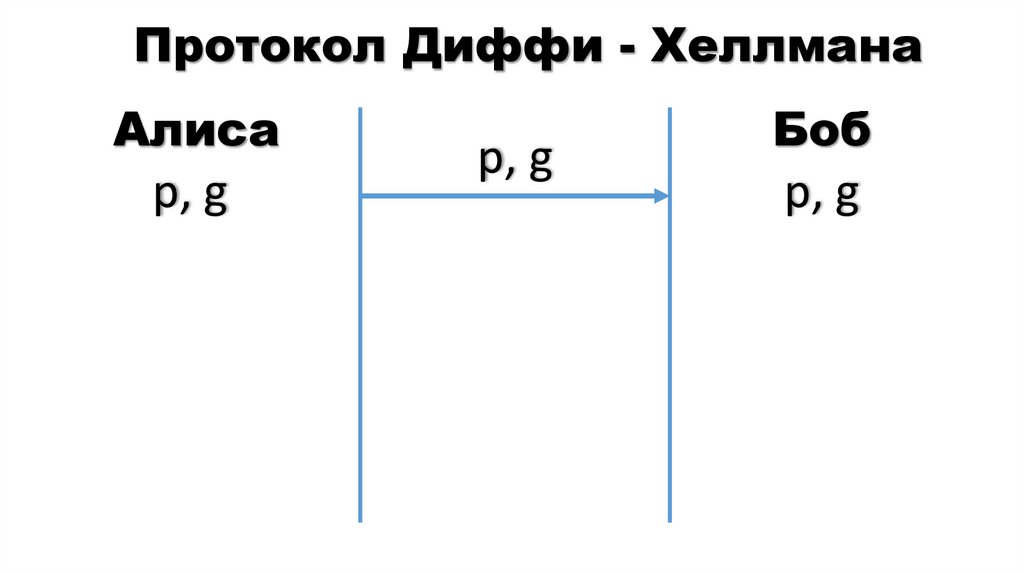
14. Протокол Диффи - Хеллмана
Алисар, g
р, g
Боб
р, g
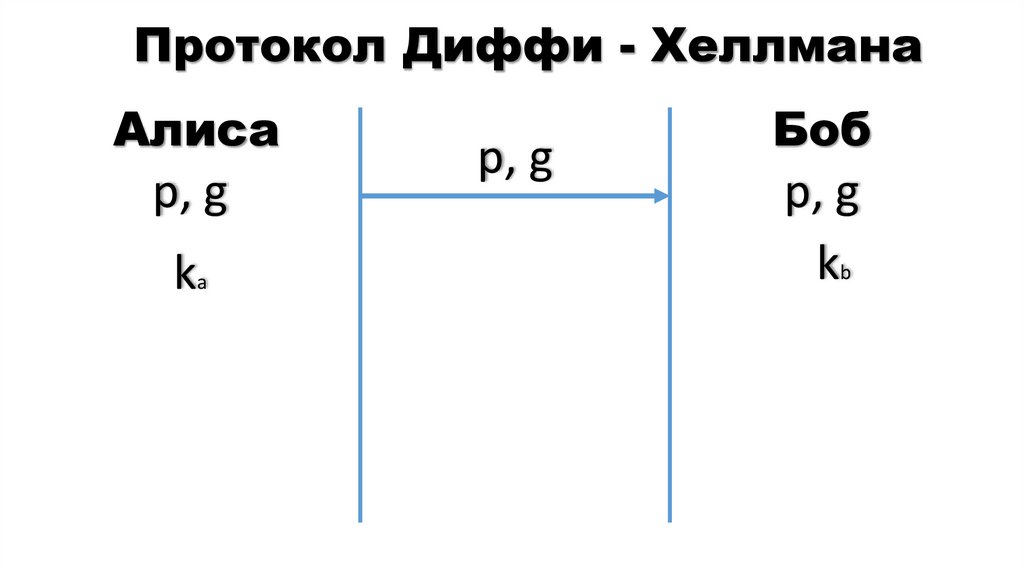
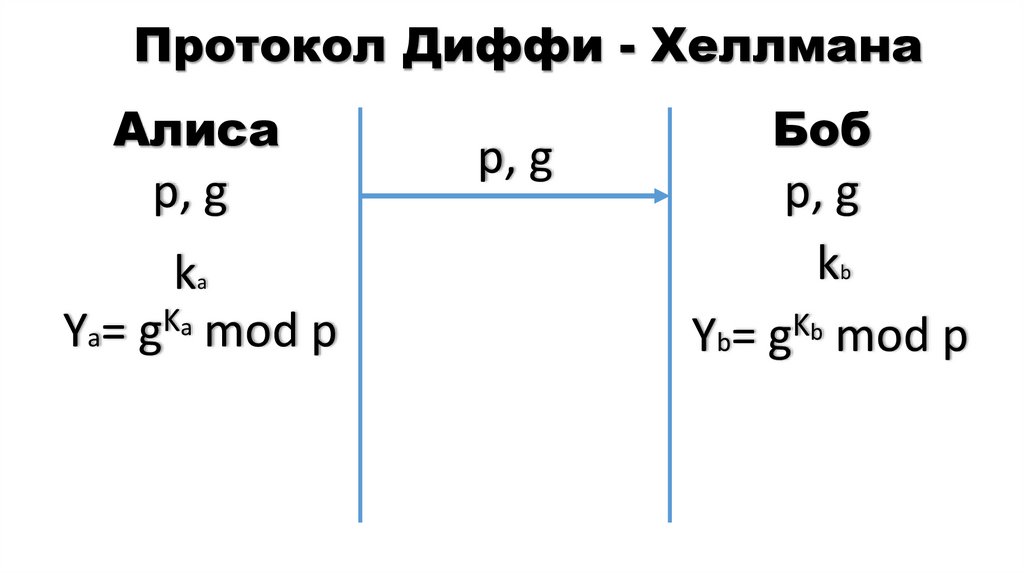
15. Протокол Диффи - Хеллмана
Алисар, g
ka
р, g
Боб
р, g
kb
16. Протокол Диффи - Хеллмана
Алисар, g
ka
K
Ya= g a mod p
р, g
Боб
р, g
kb
K
Yb= g b mod p
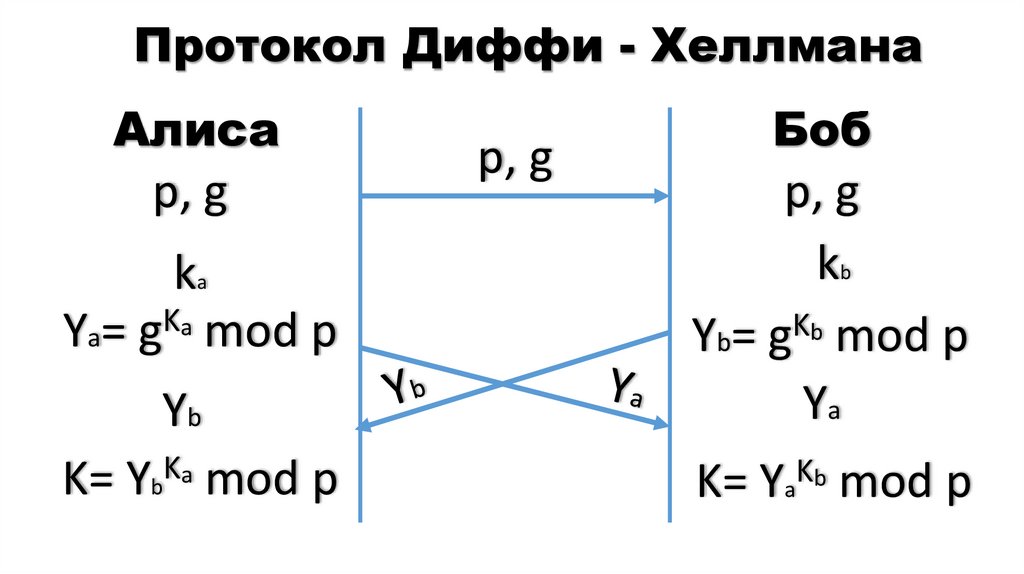
17. Протокол Диффи - Хеллмана
Алисар, g
Боб
Yb
р, g
kb
K
Yb= g b mod p
Ya
K= YbKa mod p
K
K= Ya b mod p
р, g
ka
K
Ya= g a mod p
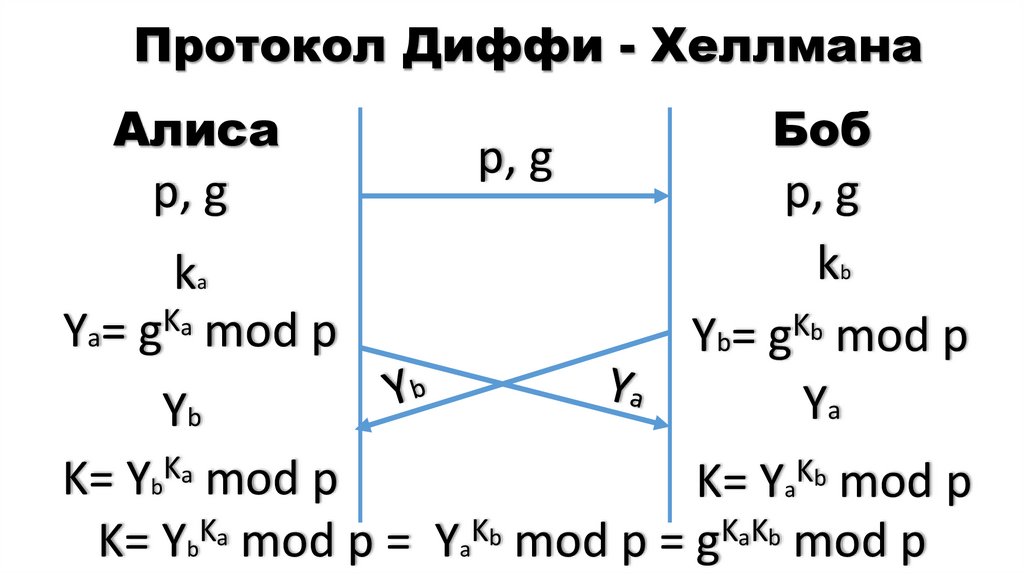
18. Протокол Диффи - Хеллмана
Алисар, g
ka
K
Ya= g a mod p
Yb
р, g
Боб
р, g
kb
K
Yb= g b mod p
Ya
K
K= YbKa mod p
K= Ya b mod p
K
K
K
K
a
b
a
K= Yb mod p = Ya mod p = g b mod p
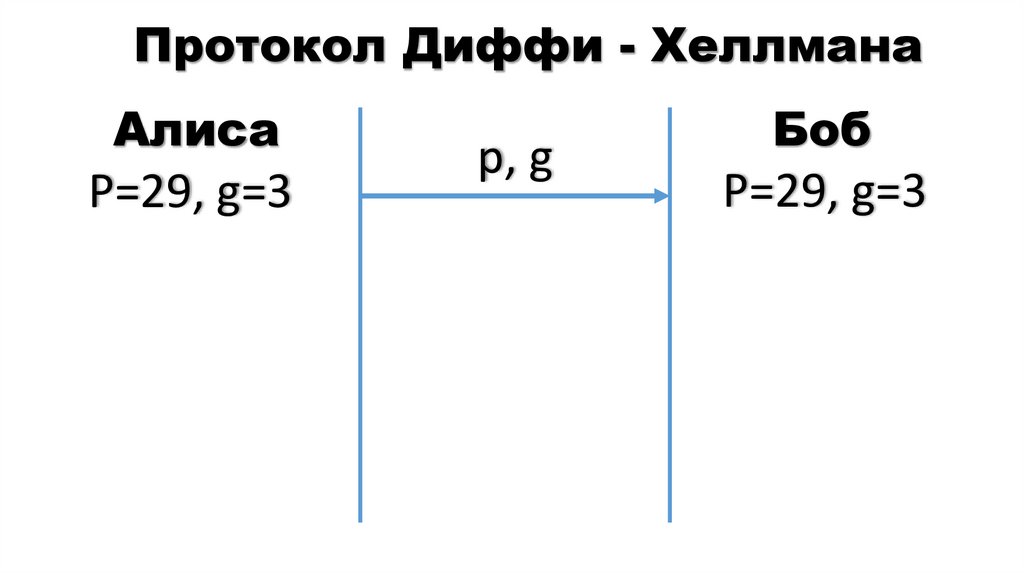
19. Протокол Диффи - Хеллмана
АлисаР=29, g=3
р, g
Боб
Р=29, g=3
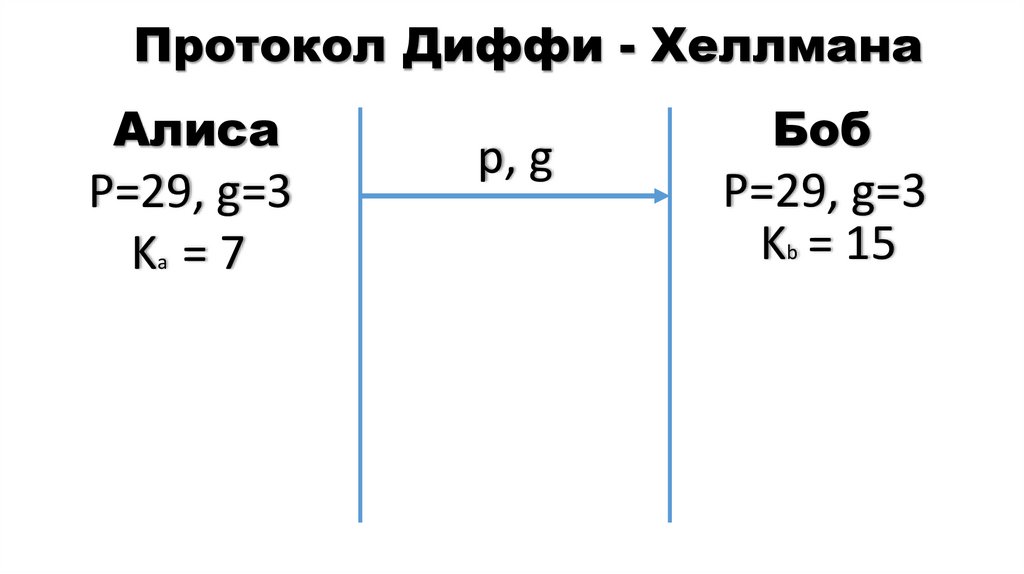
20. Протокол Диффи - Хеллмана
АлисаР=29, g=3
Ka = 7
р, g
Боб
Р=29, g=3
Kb = 15
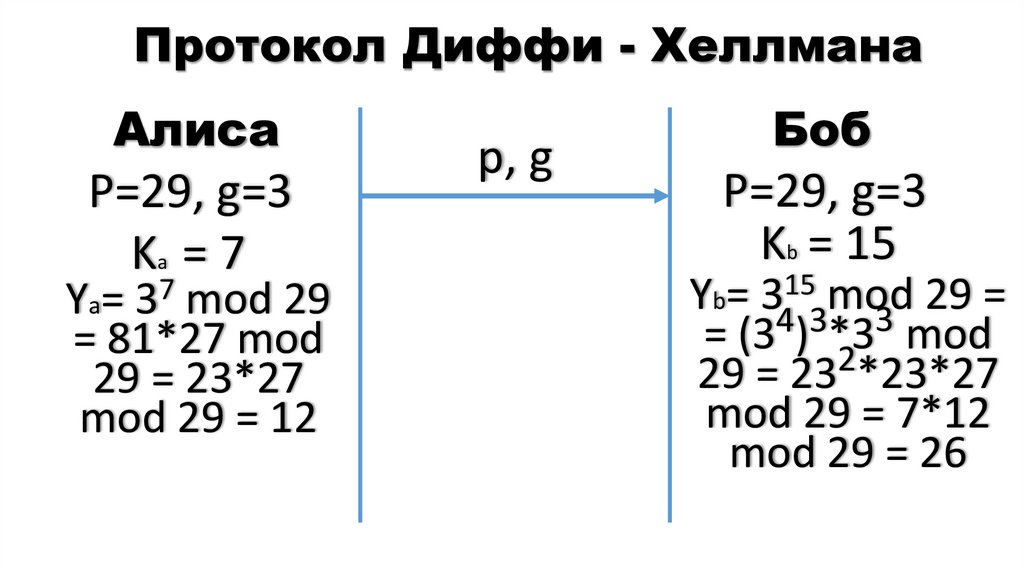
21. Протокол Диффи - Хеллмана
АлисаР=29, g=3
Ka = 7
Ya= 37 mod 29
= 81*27 mod
29 = 23*27
mod 29 = 12
р, g
Боб
Р=29, g=3
Kb = 15
Yb= 34153mod
29
=
3
= (3 ) *3
mod
2
29 = 23 *23*27
mod 29 = 7*12
mod 29 = 26
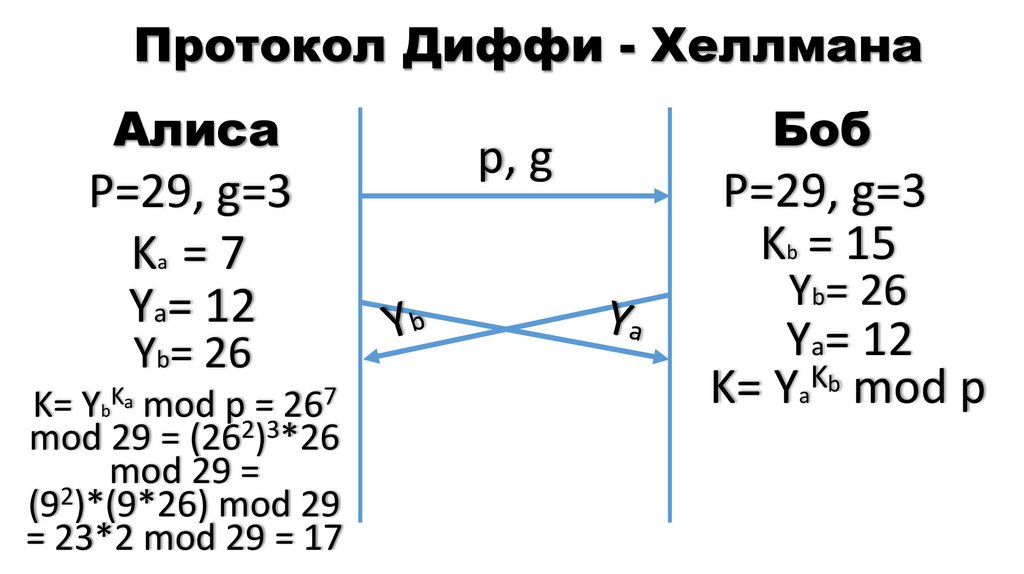
22. Протокол Диффи - Хеллмана
АлисаР=29, g=3
Ka = 7
Ya= 12
Yb= 26
K= YbKa mod p = 267
mod 29 = (262)3*26
mod 29 =
(92)*(9*26) mod 29
= 23*2 mod 29 = 17
р, g
Боб
Р=29, g=3
Kb = 15
Yb= 26
Ya= 12
K
K= Ya b mod p
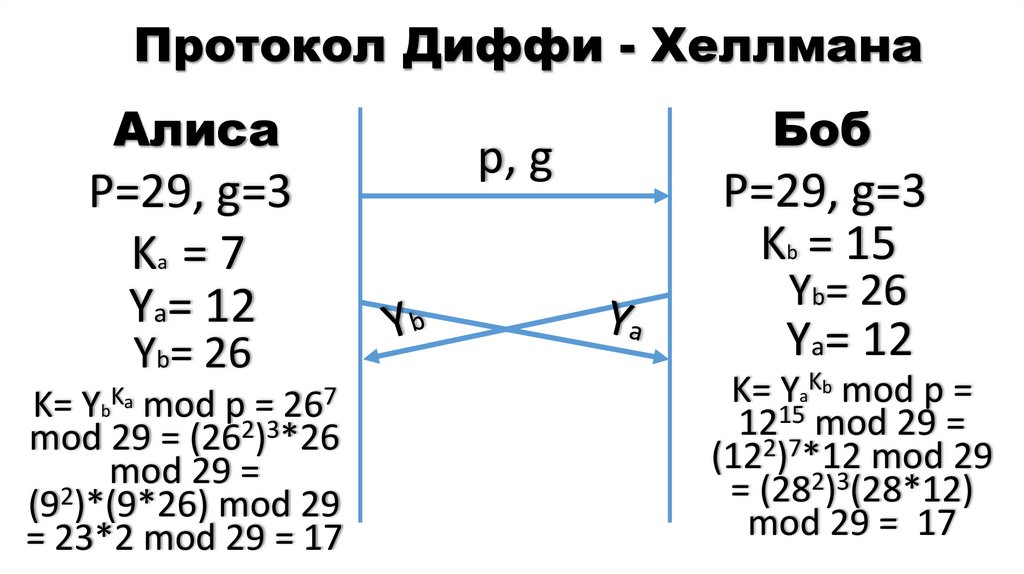
23. Протокол Диффи - Хеллмана
АлисаР=29, g=3
Ka = 7
Ya= 12
Yb= 26
K= YbKa mod p = 267
mod 29 = (262)3*26
mod 29 =
(92)*(9*26) mod 29
= 23*2 mod 29 = 17
р, g
Боб
Р=29, g=3
Kb = 15
Yb= 26
Ya= 12
K= YaKb mod p =
1215 mod 29 =
(122)7*12 mod 29
= (282)3(28*12)
mod 29 = 17
24. Алгоритм Эль-Гамаля
Тахер Эль-Гамаль (ElGamal)Опубликовано в 1984
25. Алгоритм Эль-Гамаля
Генерация ключейр – простое число,
g - первообразный корень
х – случайное число от 1 до р-1
y= gx mod p
(y, g, p) – открытый ключ,
(х, р) - закрытый ключ
26. Алгоритм Эль-Гамаля
ШифрованиеМ – сообщение, представленное в виде целого
числа от 1 до р-1
k - сессионный ключ (его знает только
отправитель)
a = gk mod p
k
b = M*y mod p
(a, b) - зашифрованный текст
27. Алгоритм Эль-Гамаля
РасшифрованиеM = b*a-X mod p
28. Алгоритм Эль-Гамаля
Расшифрование-X
M = b*a mod p
k
b = M*y mod p
a = gk mod p
x
y= g mod p
M = b*a-X mod p = M*yk*g-xk mod p =
xk
-xk
=M*g *g mod p = M
29. Алгоритм Эль-Гамаля
примерПусть для схемы Эль-Гамаля известны параметры
p = 29, g = 19, х = 22, k = 25.
Зашифруйте сообщение М = 23.
30. Алгоритм Эль-Гамаля
примерПусть для схемы Эль-Гамаля известны параметры
p = 29, g = 19, х = 22, k = 25.
Зашифруйте сообщение М = 23.
Генерация ключей
y= gx mod p
31. Алгоритм Эль-Гамаля
примерПусть для схемы Эль-Гамаля известны параметры
p = 29, g = 19, х = 22, k = 10.
Зашифруйте сообщение М = 23.
Генерация ключей
y= gx mod p
y= 1922 mod 29 = (192)11 mod 29 = (132)5 *13 mod 29
= (242)2 *(24*13)mod 29 = (252) *22 mod 29 = 4
32. Алгоритм Эль-Гамаля
примерПусть для схемы Эль-Гамаля известны параметры
p = 29, g = 19, х = 22, k = 10.
Зашифруйте сообщение М = 23.
Генерация ключей
y= gx mod p
y= 1922 mod 29 = (192)11 mod 29 = (132)5 *13 mod 29
= (242)2 *(24*13)mod 29 = (252) *22 mod 29 = 4
(4, 19, 29) – открытый ключ,
(22, 29) - закрытый ключ
33. Алгоритм Эль-Гамаля
примерЗашифруйте сообщение М = 23.
(4, 19, 29) – открытый ключ,
(22, 29) - закрытый ключ
Шифрование
Пусть k = 10.
a = gk mod p = 1910 mod 29 = (192)5 mod 29 =
2
2
2
(13 ) *13 mod 29 = (24) *13mod 29 = 6
34. Алгоритм Эль-Гамаля
примерЗашифруйте сообщение М = 23.
(4, 19, 29) – открытый ключ,
(22, 29) - закрытый ключ
Шифрование
Пусть k = 10.
a = gk mod p = 1910 mod 29 = (192)5 mod 29 =
2
2
2
(13 ) *13 mod 29 = (24) *13mod 29 = 6
b = M*yk mod p = 23*410 mod 29 = (23*16)*(44)2
mod 29 = 20 * (242) mod 29 = 7
35. Алгоритм Эль-Гамаля
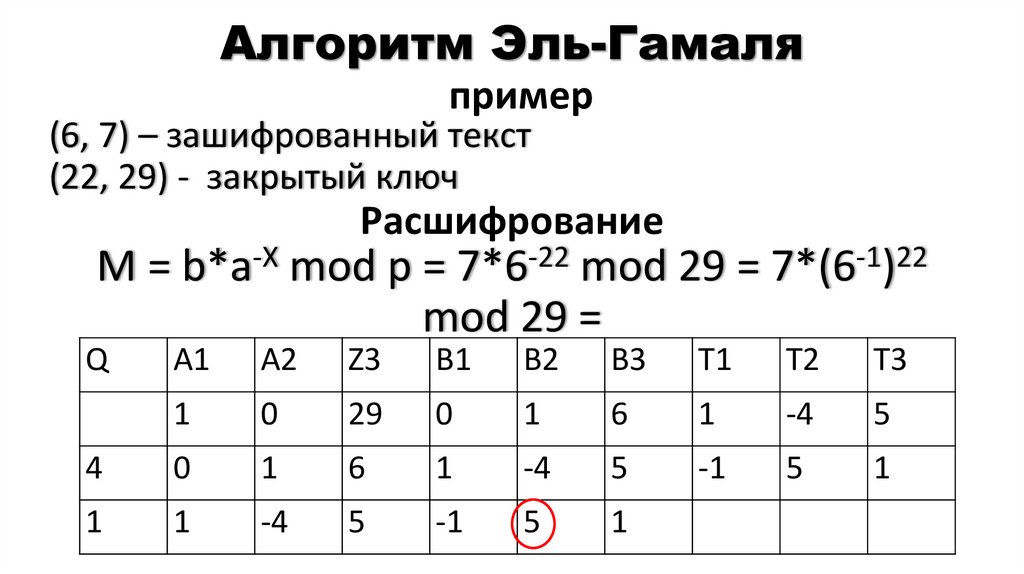
пример(6, 7) – зашифрованный текст
(22, 29) - закрытый ключ
Расшифрование
M = b*a-X mod p = 7*6-22 mod 29 = 7*(6-1)22
mod 29 =
36. Алгоритм Эль-Гамаля
пример(6, 7) – зашифрованный текст
(22, 29) - закрытый ключ
Расшифрование
-X
-22
-1
22
M = b*a mod p = 7*6 mod 29 = 7*(6 )
mod 29 =
Q
A1
A2
Z3
B1
B2
B3
T1
T2
T3
1
0
29
0
1
6
1
-4
5
4
0
1
6
1
-4
5
-1
5
1
1
1
-4
5
-1
5
1
37. Алгоритм Эль-Гамаля
пример(6, 7) – зашифрованный текст
(22, 29) - закрытый ключ
Расшифрование
M = b*a-X mod p = 7*6-22 mod 29 = 7*(6-1)22
mod 29 = 7*(5)22 mod 29 = (7*5)*(53)7 mod 29
= 6*(9)7 mod 29 = (6*9)*(92)3 mod 29 =
3
25*(23) mod 29 = 23
38. Алгоритм Эль-Гамаля
Подписьm – сообщение (или его хеш-значение),
представленное в виде целого числа от 1 до р-1
k - сессионный ключ (его знает только
подписывающий), НОД (k, fi(p)) = 1
k
r = g mod p
-1
s = (m - xr)k mod fi(p)
(r, s) - подпись.
39. Алгоритм Эль-Гамаля
Проверка подписи1. Проверяется выполнимость условий:
0 < r <p; 0 < s < p-1
2. Проверяется сравнение:
r
s
m
y r = g mod p
40. Алгоритм Эль-Гамаля
Проверка подписиr
s
m
y r = g mod p
x
y= g mod p
r = gk mod p
s = (m - xr)k-1mod fi(p)
yrrs = gxr * gks mod p = gxr * gk(m - xr)k-1 mod p =
gxr * gm * g- xr mod p = gm mod p
41. Алгоритм Эль-Гамаля
примерПодписать сообщение М = 23.
(4, 19, 29) – открытый ключ,
(22, 29) - закрытый ключ
Подпись
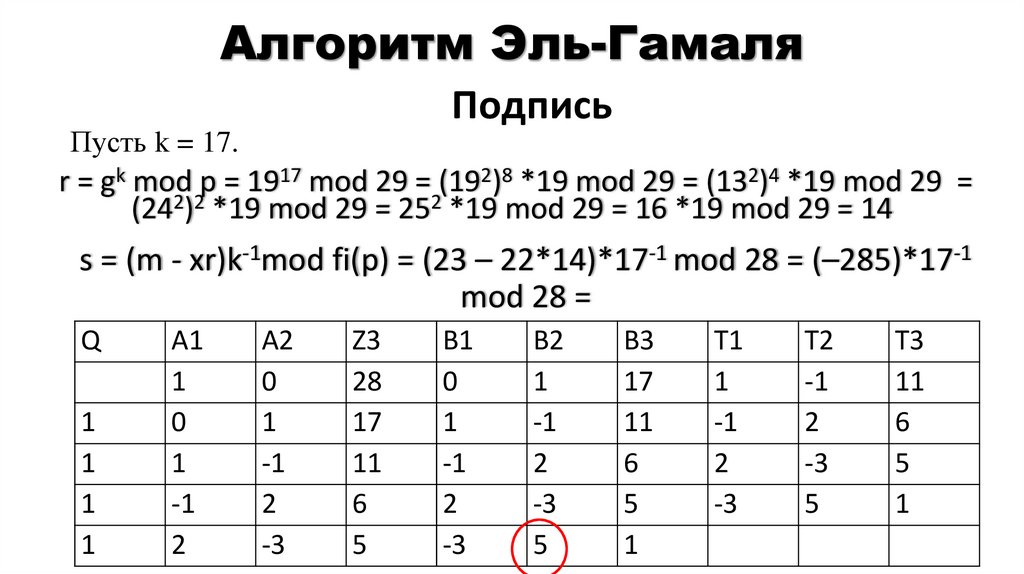
Пусть k = 17.
r = gk mod p = 1917 mod 29 = (192)8 *19 mod 29 = (132)4 *19 mod 29 =
(242)2 *19 mod 29 = 252 *19 mod 29 = 16 *19 mod 29 = 14
42. Алгоритм Эль-Гамаля
Подписать сообщение М = 23.пример
(4, 19, 29) – открытый ключ,
(22, 29) - закрытый ключ
Подпись
Пусть k = 17.
r = gk mod p = 1917 mod 29 = (192)8 *19 mod 29 = (132)4 *19 mod 29 =
(242)2 *19 mod 29 = 252 *19 mod 29 = 16 *19 mod 29 = 14
-1
s = (m - xr)k mod fi(p)
fi(p) = p – 1 = 29 – 1 = 28
43. Алгоритм Эль-Гамаля
Подписать сообщение М = 23.пример
(4, 19, 29) – открытый ключ,
(22, 29) - закрытый ключ
Подпись
Пусть k = 17.
r = gk mod p = 1917 mod 29 = (192)8 *19 mod 29 = (132)4 *19 mod 29 =
(242)2 *19 mod 29 = 252 *19 mod 29 = 16 *19 mod 29 = 14
s = (m - xr)k-1mod fi(p) = (23 – 22*14)*17-1 mod 28 = (–285)*17-1
mod 28 =
44. Алгоритм Эль-Гамаля
ПодписьПусть k = 17.
r = gk mod p = 1917 mod 29 = (192)8 *19 mod 29 = (132)4 *19 mod 29 =
(242)2 *19 mod 29 = 252 *19 mod 29 = 16 *19 mod 29 = 14
s = (m - xr)k-1mod fi(p) = (23 – 22*14)*17-1 mod 28 = (–285)*17-1
mod 28 =
Q
1
1
1
1
A1
1
0
1
-1
2
A2
0
1
-1
2
-3
Z3
28
17
11
6
5
B1
0
1
-1
2
-3
B2
1
-1
2
-3
5
B3
17
11
6
5
1
T1
1
-1
2
-3
T2
-1
2
-3
5
T3
11
6
5
1
45. Алгоритм Эль-Гамаля
Пусть k = 17.Подпись
r = gk mod p = 1917 mod 29 = (192)8 *19 mod 29 = (132)4 *19 mod 29 =
(242)2 *19 mod 29 = 252 *19 mod 29 = 16 *19 mod 29 = 14
s = (m - xr)k-1mod fi(p) = (23 – 22*14)*17-1 mod 28 = (–285)*17-1
mod 28 = (–285)*5 mod 28 = 23*5 mod 28 = 115 mod 28 = 3
(14, 3) – подпись
46. Алгоритм Эль-Гамаля
Подписать сообщение М = 23.пример
(14, 3) – подпись
(4, 19, 29) – открытый ключ,
Проверка подписи
1. Проверяется выполнимость условий:
0 < 14 <29; 0 < 3 < 28
47. Алгоритм Эль-Гамаля
примерПроверить подпись сообщения М = 23.
(14, 3) – подпись
(4, 19, 29) – открытый ключ,
Проверка подписи
1. Проверяется выполнимость условий:
0 < 14 <29; 0 < 3 < 28
r
s
14
3
2. y r mod p = 4 14 mod 29 =
48. Алгоритм Эль-Гамаля
примерПроверить подпись сообщения М = 23.
(14, 3) – подпись
(4, 19, 29) – открытый ключ,
Проверка подписи
1. Проверяется выполнимость условий:
0 < 14 <29; 0 < 3 < 28
2. yrrs mod p = 414143 mod 29 = 42 * (43)4*
(142)*14 mod 29 = 16*64*22*14 mod 29 =
16*20*18 mod 29= 18
49. Алгоритм Эль-Гамаля
примерПроверить подпись сообщения М = 23.
(14, 3) – подпись
(4, 19, 29) – открытый ключ,
Проверка подписи
1. Проверяется выполнимость условий:
0 < 14 <29; 0 < 3 < 28
2. yrrs mod p =18
3. gmmod p = 1923 mod 29 = (192)11 *19 mod 29 =
2
5
2
2
(13 ) (13*19) mod 29 = (24 ) (24*15) mod 29 =
2
(25) (12) mod 29 = 18
50. Алгоритм Эль-Гамаля
примерПроверить подпись сообщения М = 23.
(14, 3) – подпись
(4, 19, 29) – открытый ключ,
Проверка подписи
1. Проверяется выполнимость условий:
0 < 14 <29; 0 < 3 < 28
2. yrrs mod p =18
3. gmmod p = 1923 mod 29 = (192)11 *19 mod 29 =
2
5
2
2
(13 ) (13*19) mod 29 = (24 ) (24*15) mod 29 =
2
(25) (12) mod 29 = 18
































 informatics
informatics








