Similar presentations:
Асимметричное шифрование
1.
КриптографияМатематика для систем
с открытым ключом
Южный федеральный университет,
Ростов-на-Дону, 2019
sfedu.ru
2.
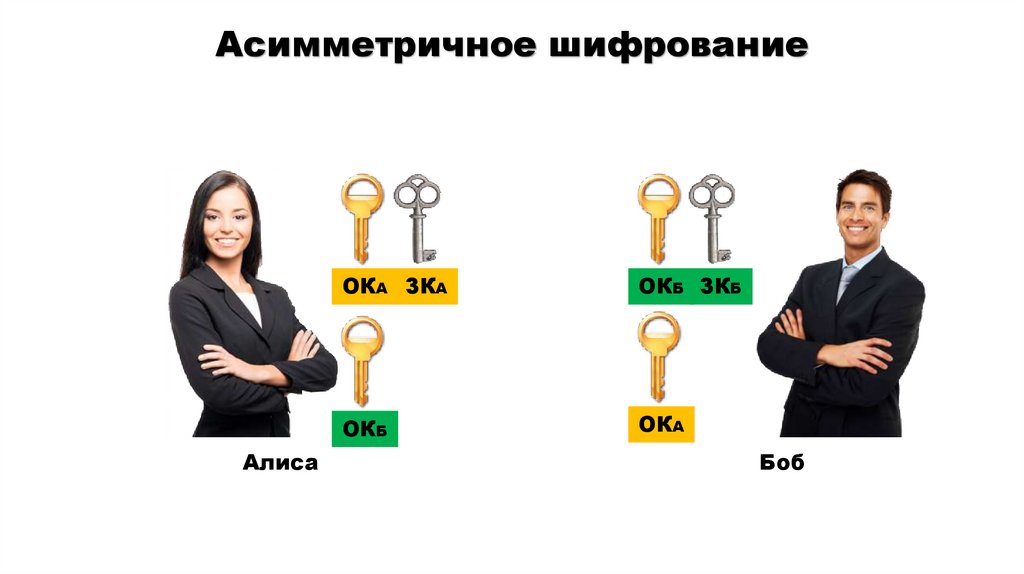
Асимметричное шифрованиеАлиса
ОКА ЗКА
ОКБ ЗКБ
ОКБ
ОКА
Боб
3.
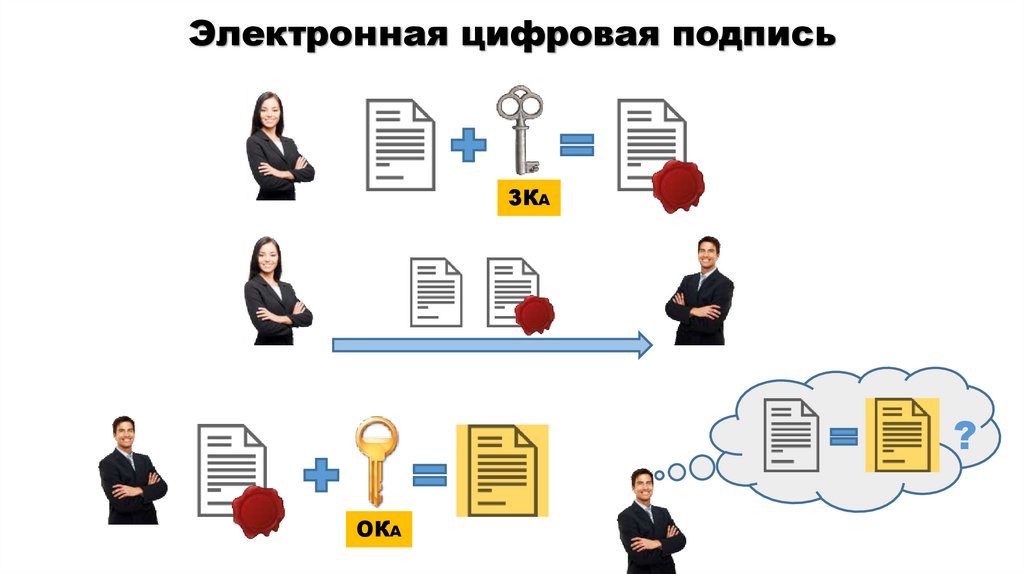
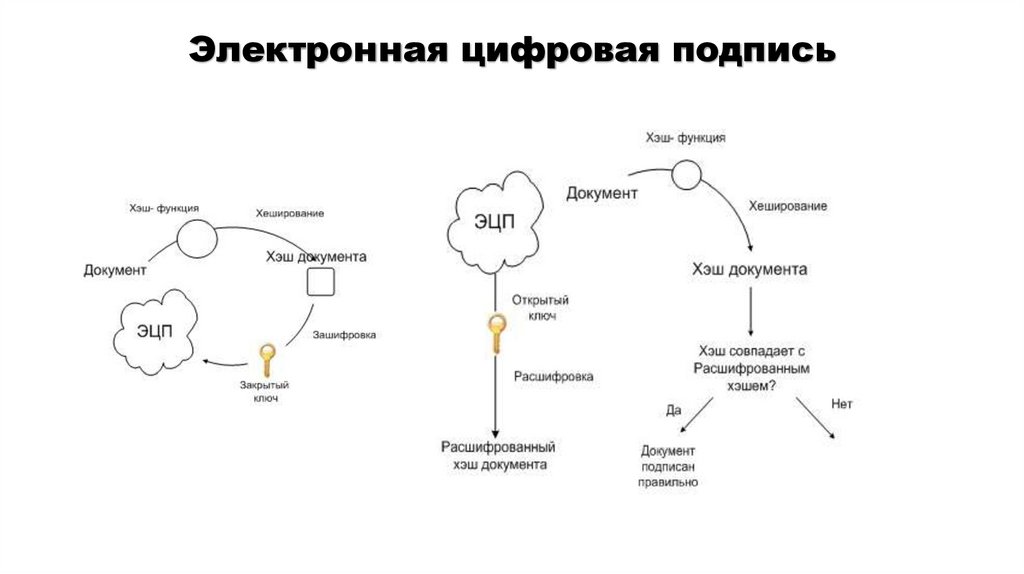
Электронная цифровая подписьЗКА
?
ОКА
4.
Электронная цифровая подпись5.
Асимметричная криптографияСимметричные криптосхемы - один ключ используется для шифрования и расшифрованная
C = E(M,K)
M = D(C,K)
Фактически, происходит подмена «большого» секрета (сообщения) «малым» (ключом)
Асимметричные криптосхемы используют ключевую пару - отдельные ключи для шифрования и расшифрования
C = E(M, Ke)
M = D(C, Kd)
Южный федеральный университет
5
6.
Шифрование и цифровая подписьПри шифровании сообщение шифруется отправителем на открытом ключе,
потом расшифровывается получателем на секретном ключе
C = E(M, Ke)
M = D(C, Kd)
При выработке цифровой подписи сообщение подписывается отправителем на секретном ключе,
потом подпись проверяется на открытом ключе
S = sign(M, Kd)
M = check(S, Ke)
Шифрование обеспечивает конфиденциальность сообщения, а цифровая подпись
- аутентичность, целостность и, при некоторых условиях, неотрицание авторства.
Южный федеральный университет
6
7.
Преимущества и недостатки асимметричнойкриптографии
Асимметричные криптосхемы решают проблему распространения ключей.
Секретный ключ хранится у получателя сообщений
Открытый ключ передаётся отправителю по незащищённым каналам связи
Проблемы:
- Открытый ключ должен быть защищён от модификации злоумышленниками во время передачи
- Асимметричные схемы работают гораздо медленнее симметричных
Южный федеральный университет
7
8.
Асимметричная криптографияСимметричные криптосхемы - один ключ используется для шифрования и расшифрованная
C = E(M,K)
M = D(C,K)
Фактически, происходит подмена «большого» секрета (сообщения) «малым» (ключом)
Асимметричные криптосхемы используют ключевую пару - отдельные ключи для шифрования и расшифрования
C = E(M, Ke)
M = D(C, Kd)
Южный федеральный университет
8
9.
Однонаправленная функцияДля конструирования асимметричных схем необходимы однонаправленные функции
Y = F(X)
Где легко вычислить Y, зная X, но сложно найти X, зная Y.
Также есть однонаправленные функции с секретом
Y = F(X) - вычислить легко
X = F-1(Y) - сложно
X = F-1(Y,S) - вычислить легко, зная секрет S
Южный федеральный университет
9
10.
Расширенный алгоритм ЕвклидаЮжный федеральный университет
10
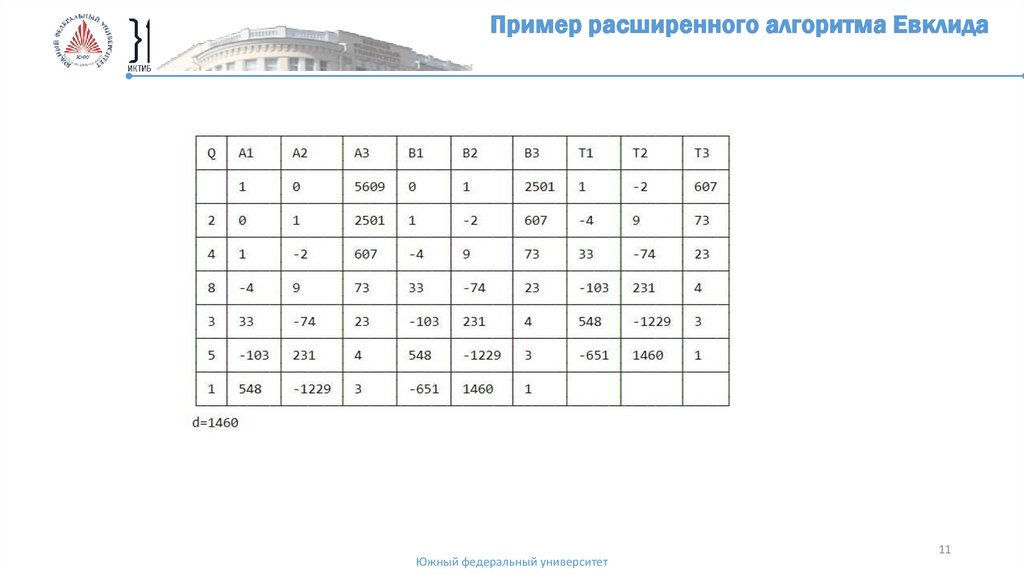
11.
Пример расширенного алгоритма ЕвклидаЮжный федеральный университет
11
12.
Модульная арифметикаВ криптографии с открытым ключом широко применяется модульная арифметика.
Операции в ней те же, что и в обычной арифметике с целыми числами.
Но после операции результат берётся по модулю p.
То есть, результатом будет остаток от деления на p.
Сложение:
a+b (mod p)
4+3 (mod 5) = 7 (mod 5) = 2
Вычитание
3-4 (mod 5) = -1 (mod 5) = 4
Умножение
3*4 (mod 5) = 12 (mod 5) = 2
a*b mod p = a mod p * b mod p
Южный федеральный университет
12
13.
Модульное делениеОперация деления в модульной арифметике не определена.
Но, её можно заменить умножением на обратный элемент.
То есть, от a/b (mod p) переходим к a*b-1 (mod p)
Обратный элемент по умножению, или мультипликативное обратное - это элемент,
который при умножении на исходное число даст 1 по модулю p
a*a-1 = 1 (mod p)
5*? = 1 mod 7
5*3 = 15 mod 7 = 1 mod 7
Например
3/5 (mod 7) = 3 * 5-1 (mod 7) = 3*3 (mod 7) = 2
Южный федеральный университет
13
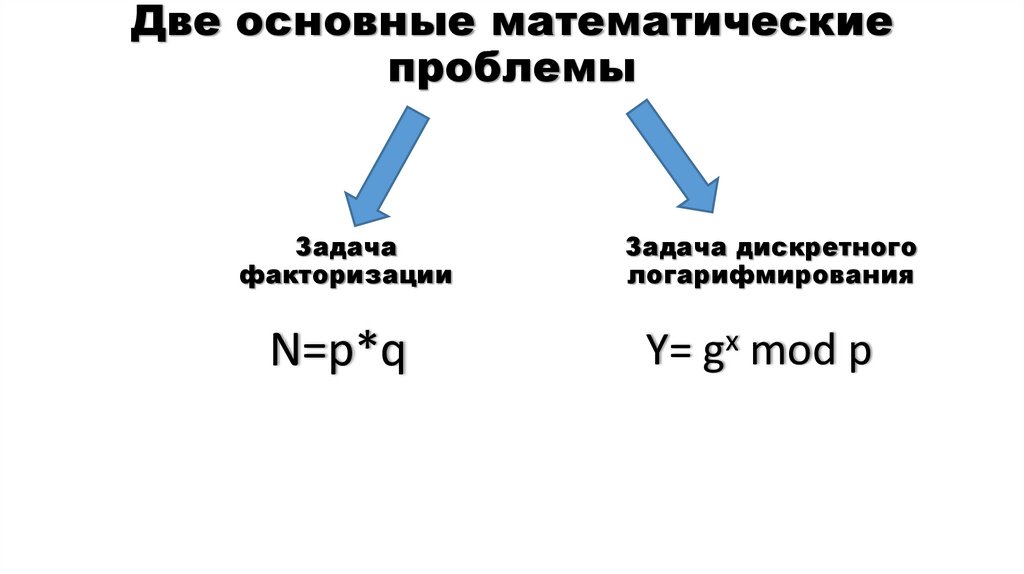
14. Две основные математические проблемы
Задачафакторизации
Задача дискретного
логарифмирования
N=p*q
Y= gx mod p
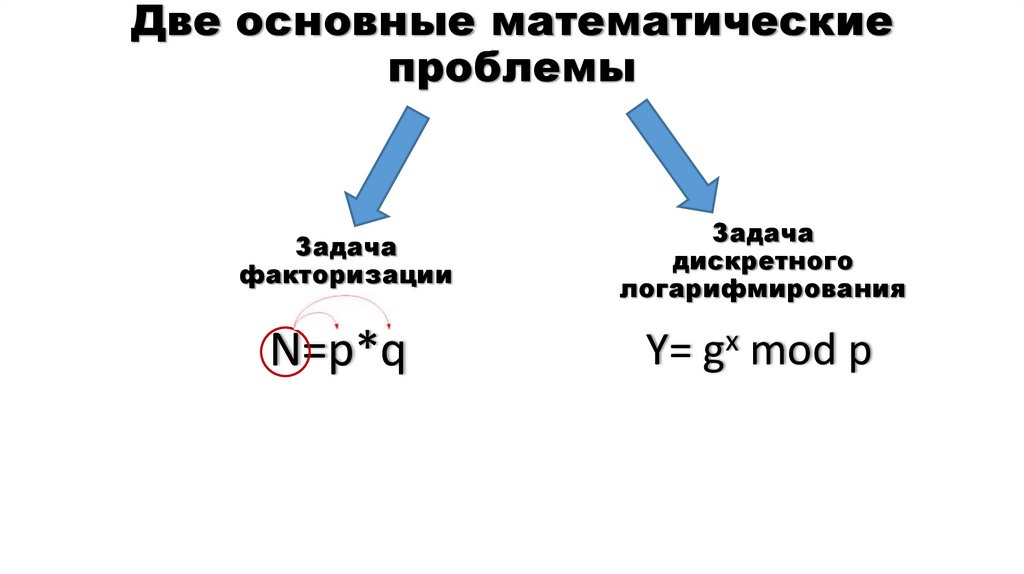
15. Две основные математические проблемы
Задачафакторизации
Задача
дискретного
логарифмирования
N=p*q
Y= gx mod p
16. Задача факторизации
N=p*qRSA-260 has 260 decimal symbols (862 bits) and has not yet been factored
RSA-260 = 2211282552952966643528108525502623092761208950247001539441374831912882294140
2001986512729726569746599085900330031400051170742204560859276357953757185954
2988389587092292384910067030341246205457845664136645406842143612930176940208
46391065875914794251435144458199
RSA-2048 has 2048 bits (617 decimal symbols). This is the largest of the RSA numbers and is
awarded a $ 200,000 prize.
RSA-2048 = 2519590847565789349402718324004839857142928212620403202777713783604366202070
7595556264018525880784406918290641249515082189298559149176184502808489120072
8449926873928072877767359714183472702618963750149718246911650776133798590957
0009733045974880842840179742910064245869181719511874612151517265463228221686
9987549182422433637259085141865462043576798423387184774447920739934236584823
8242811981638150106748104516603773060562016196762561338441436038339044149526
3443219011465754445417842402092461651572335077870774981712577246796292638635
6373289912154831438167899885040445364023527381951378636564391212010397122822120720357
https://en.wikipedia.org/wiki/RSA_numbers
17. RSA
Ron Rivest, Adi Shamir, Leonard AdlemanОпубликовано в 1977
18. Основы модулярной арифметики
Сложение:a + b (mod p)
4 + 3 (mod 5) = 7 (mod 5) = 2
Вычитание
3-4 (mod 5) = -1 (mod 5) = 4
Умножение
3 * 4 (mod 5) = 12 (mod 5) = 2
a * b mod p = a mod p * b mod p
Деление:
Мы не можем делить, но можем
умножать на мультипликативное
обратное
a*a-1 mod p = 1 mod p
2*a-1 mod p = 1 mod p
2*? mod p = 1 mod 11
19. Основы модулярной арифметики
Сложение:a + b (mod p)
4 + 3 (mod 5) = 7 (mod 5) = 2
Вычитание
3-4 (mod 5) = -1 (mod 5) = 4
Умножение
3 * 4 (mod 5) = 12 (mod 5) = 2
a * b mod p = a mod p * b mod p
Деление:
Мы не можем делить, но можем
умножать на мультипликативное
обратное
a*a-1 mod p = 1 mod p
2*a-1 mod p = 1 mod p
2*? mod p = 1 mod 11
2*6 mod 11 = 1 mod 11
Расширенный алгоритм Евклида
20. Some important theorems
Если р простое число, тоap-1(mod p)=1 малая теорема Ферма)
Для любого m (простого или составного) и любого a взаимнопростого с m,
выполняется следующее соотношение:
(Теорема Эйлера)
φ (m) = m – 1 если m простое число
φ (m) = (m1 – 1) * (m2 – 1) * … *(mk - 1) если m составное число
m = m1*m2*…*mk
21. RSA (генерация ключа)
Пусть p и q - два простых числа22. RSA (генерация ключа)
Пусть p и q - два простых числаНайдем их произведение: n = p * q
23. RSA (генерация ключа)
Пусть p и q - два простых числаНайдем их произведение: n = p * q
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1)
24. RSA (генерация ключа)
Пусть p и q - два простых числаНайдем их произведение: n = p * q
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1)
Выберем e, взаимнопростое с φ (n)
(то есть НОД (e, φ (n)) = 1)
25. RSA (генерация ключа)
Пусть p и q - два простых числаНайдем их произведение: n = p * q
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1)
Выберем e, взаимнопростое с φ (n)
(то есть НОД (e, φ (n)) = 1)
Найдем d: d = e-1 mod φ (n) такое что d*e = 1 mod φ (n)
26. RSA (генерация ключа)
Пусть p и q - два простых числаНайдем их произведение: n = p * q
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1)
Выберем e, взаимнопростое с φ (n)
(то есть НОД (e, φ (n)) = 1)
Найдем d: d = e-1 mod φ (n) такое что d*e = 1 mod φ (n)
Открытым ключом будет пара чисел (e, n)
Закрытым ключом будет пара чисел (d, n)
27. RSA (шифрование)
Открытым ключом будет пара чисел (e, n)Закрытым ключом будет пара чисел (d, n)
C = Me (mod n)
M = Cd (mod n)
28. RSA (подпись)
Открытым ключом будет пара чисел (e, n)Закрытым ключом будет пара чисел (d, n)
S = Md (mod n)
M = Se (mod n)
29. RSA (пример)
Пусть p и q - два простых числа: p = 7 q=1130. RSA (пример)
Пусть p и q - два простых числа: p = 7 q=11Найдем их произведение: n = p * q = 7*11 = 77
31. RSA (пример)
Пусть p и q - два простых числа: p = 7 q=11Найдем их произведение: n = p * q = 7*11 = 77
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1) = 6*10 = 60
32. RSA (пример)
Пусть p и q - два простых числа: p = 7 q=11Найдем их произведение: n = p * q = 7*11 = 77
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1) = 6*10 = 60
Выберем e, взаимнопростое с φ (n)
(то есть НОД (e, φ (n)) = 1)
φ (n) = 60 = 2*2*3*5 e = 13
33. RSA (пример)
Пусть p и q - два простых числа: p = 7 q=11Найдем их произведение: n = p * q = 7*11 = 77
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1) = 6*10 = 60
Выберем e, взаимнопростое с φ (n)
(то есть НОД (e, φ (n)) = 1)
φ (n) = 60 = 2*2*3*5 e = 13
Найдем d: d = e-1 mod φ (n) такое что d*e = 1 mod φ (n)
d = 37 13*37 mod 60 = 481 mod 60 = 1
https://planetcalc.com/3298/
34. RSA (пример)
Пусть p и q - два простых числа: p = 7 q=11Найдем их произведение: n = p * q = 7*11 = 77
Вычислим функцию Эйлера: φ (n) = (p-1)*(q-1) = 6*10 = 60
Выберем e, взаимнопростое с φ (n)
(то есть НОД (e, φ (n)) = 1)
φ (n) = 60 = 2*2*3*5 e = 13
Найдем d: d = e-1 mod φ (n) такое что d*e = 1 mod φ (n)
d = 37 13*37 mod 60 = 481 mod 60 = 1
Открытым ключом будет пара чисел (e, n) = (13, 77)
Закрытым ключом будет пара чисел (d, n) = (37, 77)
35. RSA (пример)
Открытым ключом будет пара чисел (e, n) = (13, 77)Закрытым ключом будет пара чисел (d, n) = (37, 77)
Пусть сообщение M=15
36. RSA (пример)
Открытым ключом будет пара чисел (e, n) = (13, 77)Закрытым ключом будет пара чисел (d, n) = (37, 77)
Пусть сообщение M=15
Зашифрование:
C = Me mod n = 1513 mod 77 = 64
https://planetcalc.com/8979/
37. RSA (пример)
Открытым ключом будет пара чисел (e, n) = (13, 77)Закрытым ключом будет пара чисел (d, n) = (37, 77)
Пусть сообщение M=15
Зашифрование:
C = Me mod n = 1513 mod 77 = 64
Расшифрование:
M = Cd mod n = 6437 mod 77 = 15
38. RSA (пример)
Открытым ключом будет пара чисел (e, n) = (13, 77)Закрытым ключом будет пара чисел (d, n) = (37, 77)
Пусть сообщение M=15
Подпись:
S = Md mod n = 1537 mod 77 = 71
39. RSA (пример)
Открытым ключом будет пара чисел (e, n) = (13, 77)Закрытым ключом будет пара чисел (d, n) = (37, 77)
Пусть сообщение M=15
Подпись:
S = Md mod n = 1537 mod 77 = 71
Проверка подписи:
M = Se mod n = 7113 mod 77 = 15

































 informatics
informatics