Входной контроль. Цель и задачи математики при освоении специальности. Тема 1.1

1.

Повторение школьного курса математики
Тема 1.1 . ВХОДНОЙ КОНТРОЛЬ Цель и задачи математики
при освоении специальности
Тема 1.2 . Числа и вычисления. Выражения и их
преобразования
Тема 1.3 . Уравнения и неравенства
Тема 1.4 . Системы уравнений и неравенств
5 занятий + Контрольная работа

2.

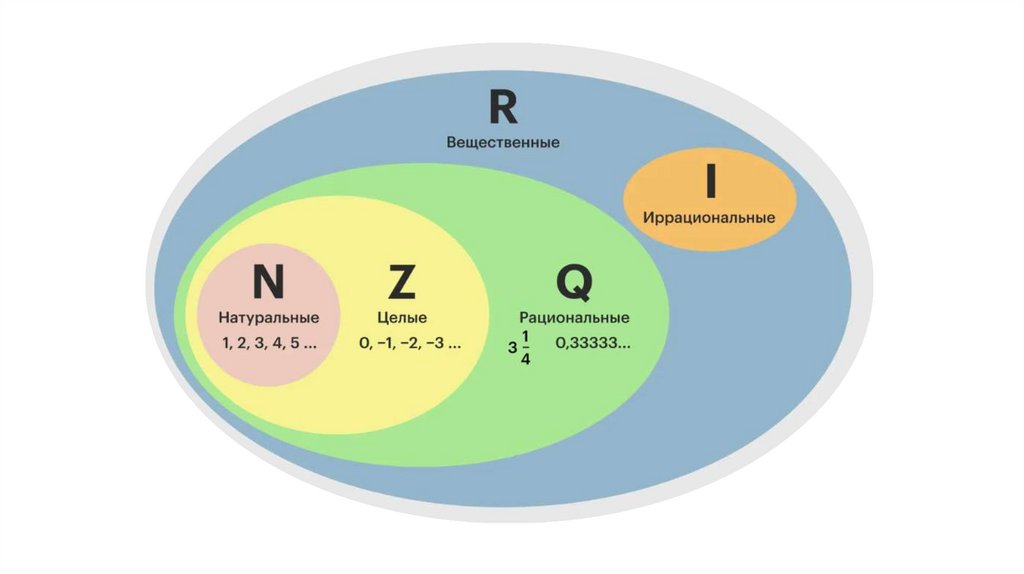
Тема урока:
Расширение понятия числа
Действительные числа

3.

Числа, употребляемые при счете предметов,
называются натуральными.
-{1;2;3;………..} - множество всех натуральных чисел

4.

Объединение множества натуральных чисел
и множества, состоящего из одного элемента НУЛЬ,
есть множество неотрицательных целых чисел
-{0;1;2;3;………..} - множество неотрицательных
целых чисел

5.

Натуральные числа, числа, противоположные
натуральным, и нуль составляют множество
целых чисел.
-{…-3;-2;-1;0;1;2;3;………..} - множество целых чисел

6.

Целые и дробные числа составляют множество
рациональных чисел
Любое рациональное число может быть записано в
виде несократимой дроби
, где m
,n
т.е. числитель – целое число, знаменатель - натуральное

7.

Любое рациональное число представимо в виде
бесконечной десятичной дроби а0,а1а2а3а4…., где
а0 - целая часть
аi ,i – 1,2,3,…. – целые числа, удовлетворяющие
неравенству 0<=a i <=9
В записи рациональных чисел в виде бесконечных десятичных дробей , начиная с
некоторого места , все десятичные знаки у этих дробей начинают повторяться.
Например , 0,25000000000…… или 0,555555………..
Такие дроби получили название бесконечных периодических десятичных дробей

8.

Рациональные и иррациональные числа составляют
множество
действительных чисел

9.

Множество рациональных чисел
является подмножеством
действительных чисел

10.

Действительные числа, не являющиеся рациональными,
называются иррациональными
Множество иррациональных чисел является
подмножеством действительных чисел