Определение комплексного числа Формы записи комплексных чисел. Урок 1

1. Урок 1. Определение комплексного числа Формы записи комплексных чисел

УРОК 1. ОПРЕДЕЛЕНИЕ
КОМПЛЕКСНОГО ЧИСЛА
ФОРМЫ ЗАПИСИ
КОМПЛЕКСНЫХ ЧИСЕЛ
Раздел 1. Основы теории комплексных чисел

2. План урока

ПЛАН УРОКА
1. Определение комплексного числа
2. Форма записи комплексного числа
3. Арифметические операции над комплексными числами
4. Геометрическое изображение комплексных чисел
5. Примеры
6. Домашнее задание

3. Определение комплексного числа

ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО ЧИСЛА
Комлексные числа (мнимые числа) – класс математических
объектов вида:
z=x+yi , где x,y – действительные числа
i – мнимая единица
При этом x – действительная часть (x=Re z)
y – мнимая часть (y=Im z)
i ² = -1

4. Определение комплексного числа

ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО ЧИСЛА
Два комплексных числа считаются равными тогда и только
тогда, когда равны их действительные и мнимые части
С – множество всех комплексных чисел
z ∈ С, z=x+yi
z (x,y)

5. Арифметические операции

АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ
С помощью операций сложения и умножения действительных
чисел в множестве комплексных чисел также можно ввести
операции сложения и умножения:
Вычитание и деление определяются как действия, обратные
сложению и умножению соответственно

6. Форма записи комплексных чисел

ФОРМА ЗАПИСИ КОМПЛЕКСНЫХ ЧИСЕЛ
Множество всех элементов x + yi, в котором заданы
операции сложения, вычитания, умножения и деления
согласно выше сформулированным правилам,
называется множеством комплексных чисел, а каждый его
элемент - комплексным числом
Обозначение x + yi комплексных чисел называется
их алгебраической формой записи

7. Векторная итерпретация

ВЕКТОРНАЯ ИТЕРПРЕТАЦИЯ
Комплексное число z = x + yi можно рассматривать как вектор на плоскости с
координатами x,y. Этот вектор мы будем обозначать той же буквой z = (x,y)
Координатная плоскость, векторы z = (x,y) которой интерпретируются как
комплексные числа, называется комплексной плоскостью, ее ось x действительной осью, а ось y - мнимой
Длина |z| вектора z = (x,y) называется модулем или абсолютной величиной
комплексного числа z = x + yi. Очевидно,

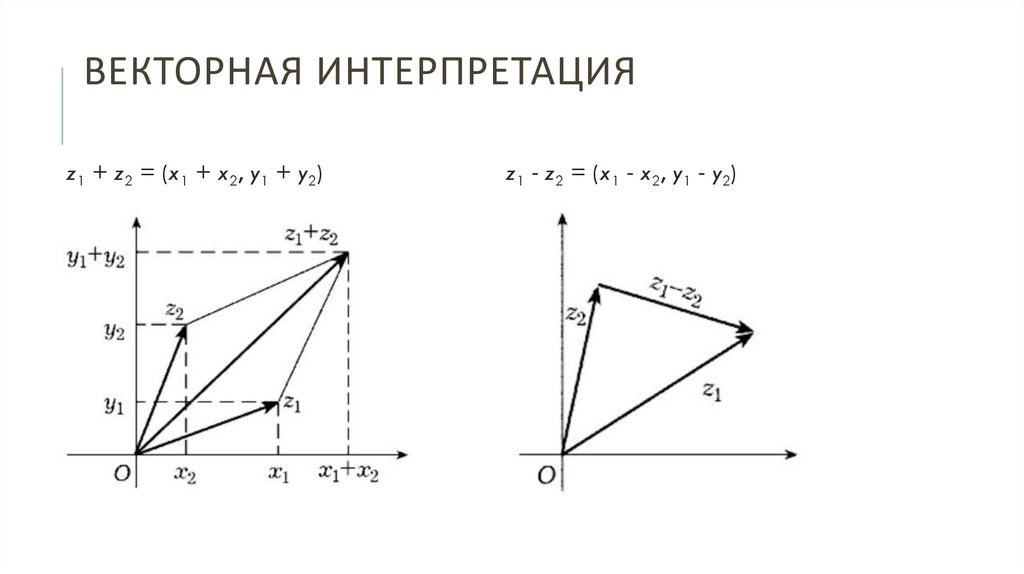
8. Векторная интерпретация

ВЕКТОРНАЯ ИНТЕРПРЕТАЦИЯ
z1 + z2 = (x1 + x2, y1 + y2)
z1 - z2 = (x1 - x2, y1 - y2)

9. Пример 1. деление комплексных чисел

ПРИМЕР 1. ДЕЛЕНИЕ КОМПЛЕКСНЫХ
ЧИСЕЛ

10. Пример 2. вычислить значение выражения

ПРИМЕР 2. ВЫЧИСЛИТЬ ЗНАЧЕНИЕ
ВЫРАЖЕНИЯ

11. Домашнее задание

ДОМАШНЕЕ ЗАДАНИЕ

12. Дорогу осилит идущий!

ДОРОГУ ОСИЛИТ ИДУЩИЙ!