Лекция № 15 Алгоритмы поиска потока

1. Кафедра системы сбора и обработки информации

ВОЕННО-КОСМИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ А.Ф. МОЖАЙСКОГО
Кафедра системы сбора и обработки информации
Дискретная математика
Лекция № 15
Алгоритмы поиска потока
Андрушкевич С.С..

2.

2
Лекция № 15. Алгоритмы поиска потока
Цель: сформулировать основные подходы к построению потоков и
изучить подходы к решению оптимизационных задач на графах по
их построению
Учебные вопросы:
1. Алгоритм поиска увеличивающей цепи.
2. Алгоритм поиска максимального
Фалкерсона)
потока
(Форда-

3. Учебный вопрос № 1

1. Алгоритм поиска увеличивающей цепи
3

4.

4
Теорема Форда – Фолкерсона. Величина максимального потока в сети из
вершины s в вершину t равна величине минимального сечения между
этими вершинами.
Пусть имеется граф, в котором некоторое количество единиц потока
проходит от источника к стоку и для каждой единицы потока известен
маршрут движения. Количество единиц, проходящих по дуге (х, у),
называется потоком в данной дуге. Поток в дуге (х, у) обозначается
через f(x, у).
0 ≤ f(x,у)≤ с(х, у) - пропускная способность.

5.

5
Дуги графа можно отнести к трем различным категориям:
Дуги, в которых поток не может ни увеличиваться, ни уменьшаться (N);
Дуги, в которых поток может увеличиваться (I);
Дуги, в которых поток может уменьшаться (R).
Дуги из множества I называются увеличивающими, а дуги из множества
R - уменьшающими

6.

6
Алгоритм поиска увеличивающей цепи
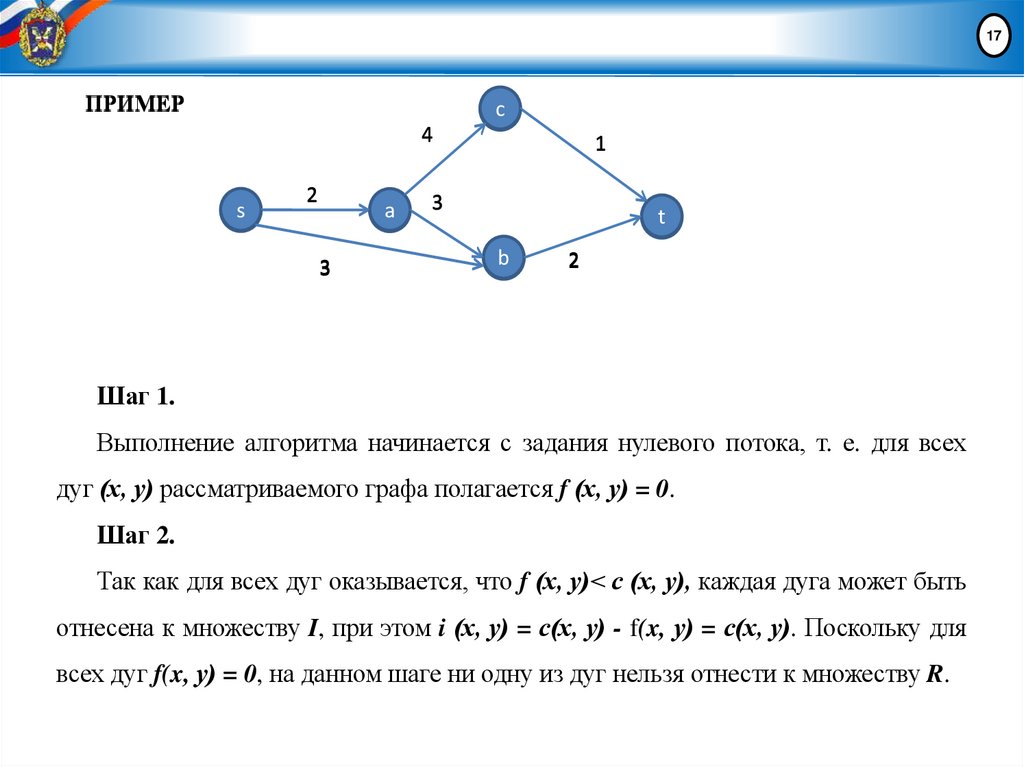
Шаг 1.
Определить состав множеств N, I и R. Дуги множества N из
дальнейшего рассмотрения исключить (поскольку в них изменения
потока невозможны). Окрасить вершину s.
Шаг 2.
Окрашивать дуги и вершины в соответствии с приводимыми правилами
до тех пор, пока либо не будет окрашена вершина t, либо окраска новых
вершин станет невозможной.
Правила окрашивания вершины у и дуги (х, у) при уже окрашенной вершине х
состоят в следующем:
1) если (х, у) ∈ I, то окрашиваются вершина у и дуга (х, у);
2) если (у, х) ∈ R, то опрашиваются вершина у и дуга (у, х);
3) в противном случае окрашивание вершины у и дуги (х, у) не производится.

7.

7
В случае окрашивания вершины t
в сети находится
единственная цепь из s в t, включающая окрашенные дуги. (Эта
цепь является увеличивающей.) В противном случае, т. е. когда по
окончании процедуры окрашивания вершина t не окрашивается, в
сети отсутствуют увеличивающие цепи из s в t.

8.

8
ПРИМЕР
R
a
b
IR
I
I
s
N
R
R
R
t
N
c
d
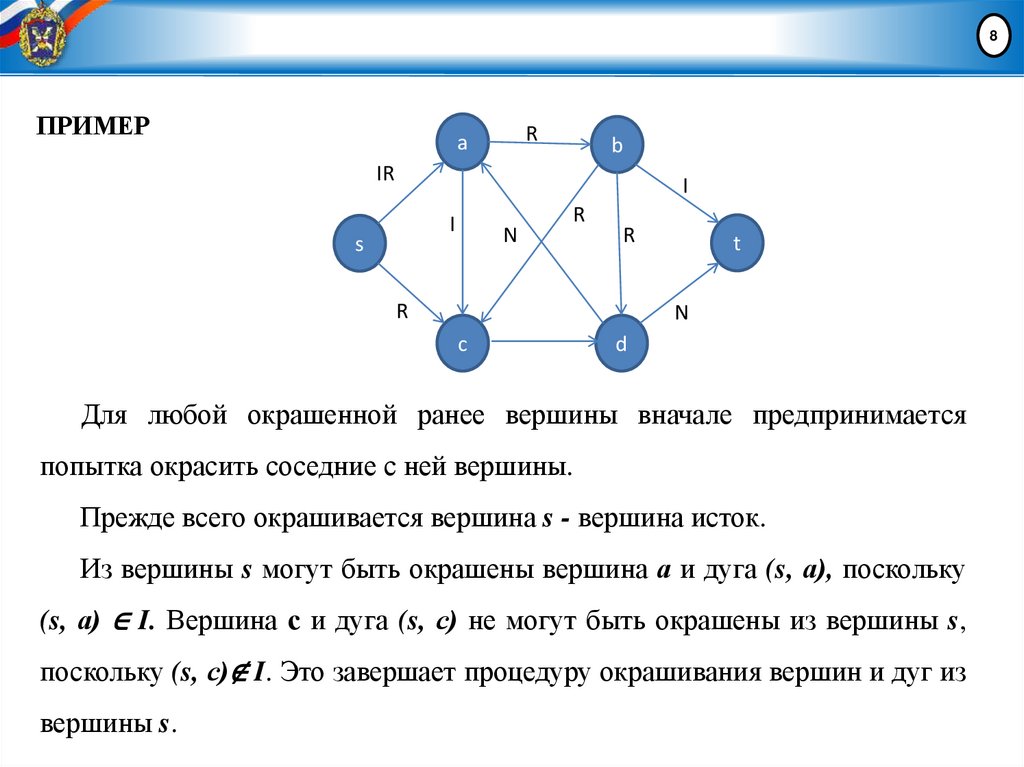
Для любой окрашенной ранее вершины вначале предпринимается
попытка окрасить соседние с ней вершины.
Прежде всего окрашивается вершина s - вершина исток.
Из вершины s могут быть окрашены вершина а и дуга (s, а), поскольку
(s, а) ∈ I. Вершина с и дуга (s, с) не могут быть окрашены из вершины s,
поскольку (s, с)∉ I. Это завершает процедуру окрашивания вершин и дуг из
вершины s.

9.

9
IR
I
s
R
a
N
b
R
I
R
R
c
d
t
N
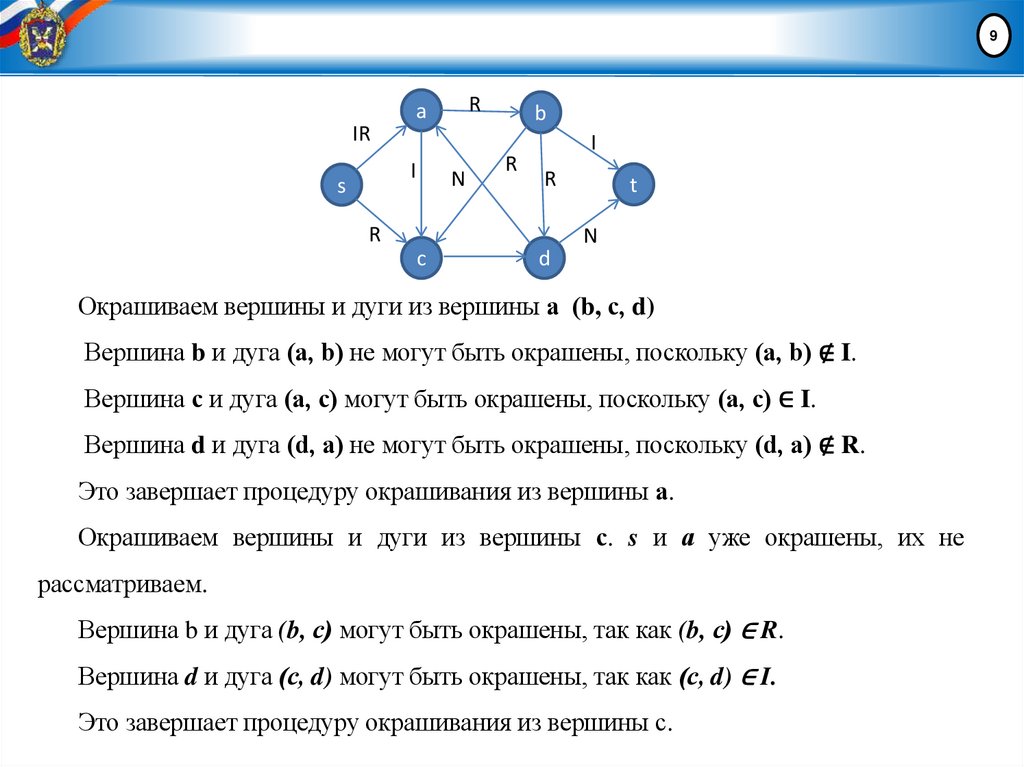
Окрашиваем вершины и дуги из вершины а (b, с, d)
Вершина b и дуга (а, b) не могут быть окрашены, поскольку (а, b) ∉ I.
Вершина с и дуга (а, с) могут быть окрашены, поскольку (а, с) ∈ I.
Вершина d и дуга (d, а) не могут быть окрашены, поскольку (d, а) ∉ R.
Это завершает процедуру окрашивания из вершины а.
Окрашиваем вершины и дуги из вершины с. s и а уже окрашены, их не
рассматриваем.
Вершина b и дуга (b, с) могут быть окрашены, так как (b, с) ∈ R.
Вершина d и дуга (с, d) могут быть окрашены, так как (с, d) ∈ I.
Это завершает процедуру окрашивания из вершины с.

10. Учебный вопрос № 1

R
a
b
I
I
s
a
b
IR
10
N
R
R
t
N
c
d
t
s
R
c
d
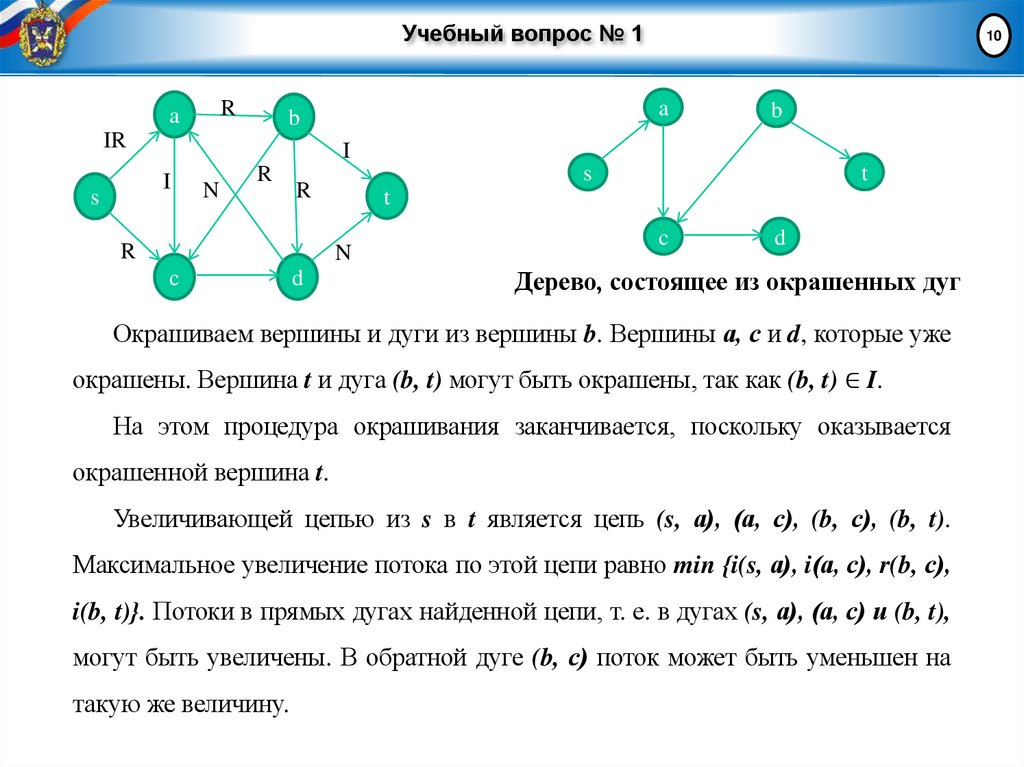
Дерево, состоящее из окрашенных дуг
Окрашиваем вершины и дуги из вершины b. Вершины а, с и d, которые уже
окрашены. Вершина t и дуга (b, t) могут быть окрашены, так как (b, t) ∈ I.
На этом процедура окрашивания заканчивается, поскольку оказывается
окрашенной вершина t.
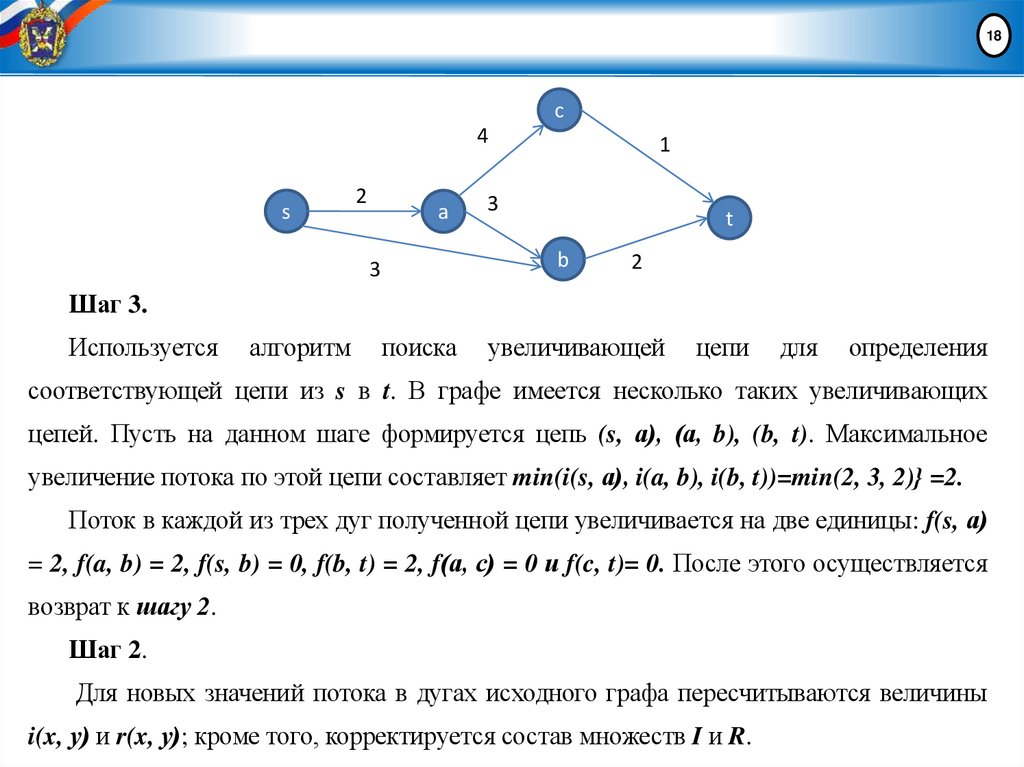
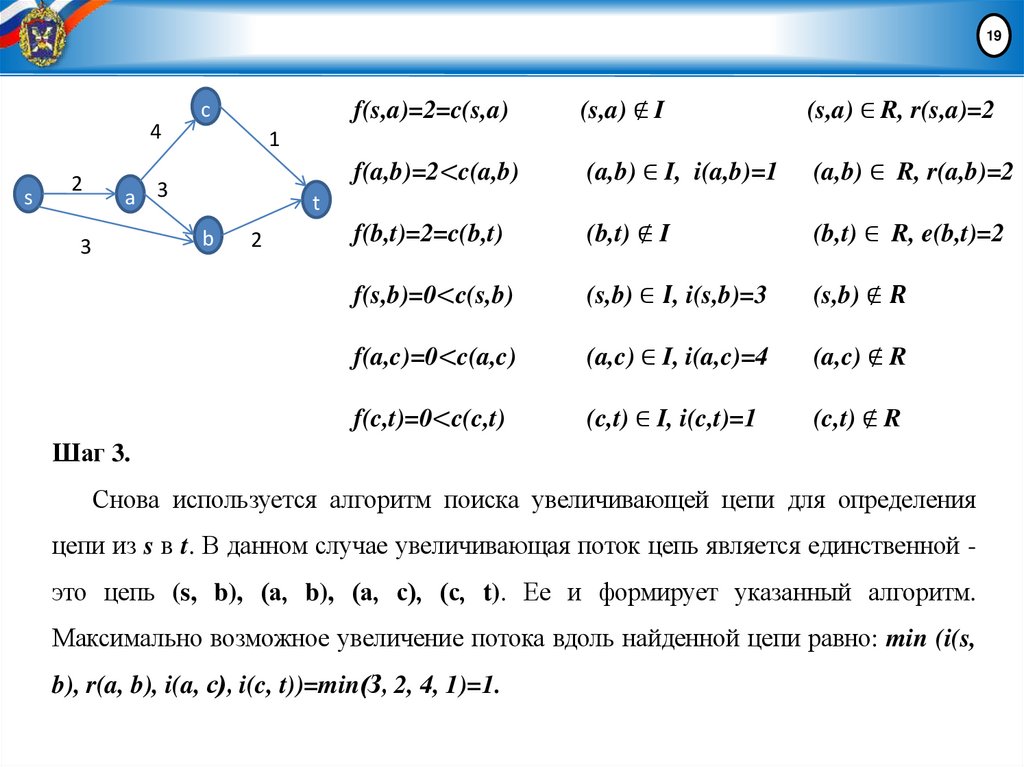
Увеличивающей цепью из s в t является цепь (s, а), (а, с), (b, с), (b, t).
Максимальное увеличение потока по этой цепи равно min {i(s, а), i(а, с), r(b, с),
i(b, t)}. Потоки в прямых дугах найденной цепи, т. е. в дугах (s, а), (а, с) и (b, t),
могут быть увеличены. В обратной дуге (b, с) поток может быть уменьшен на
такую же величину.

11.

11
Алгоритм поиска максимального потока (Форда-Фалкерсона)

12. Учебный вопрос № 1

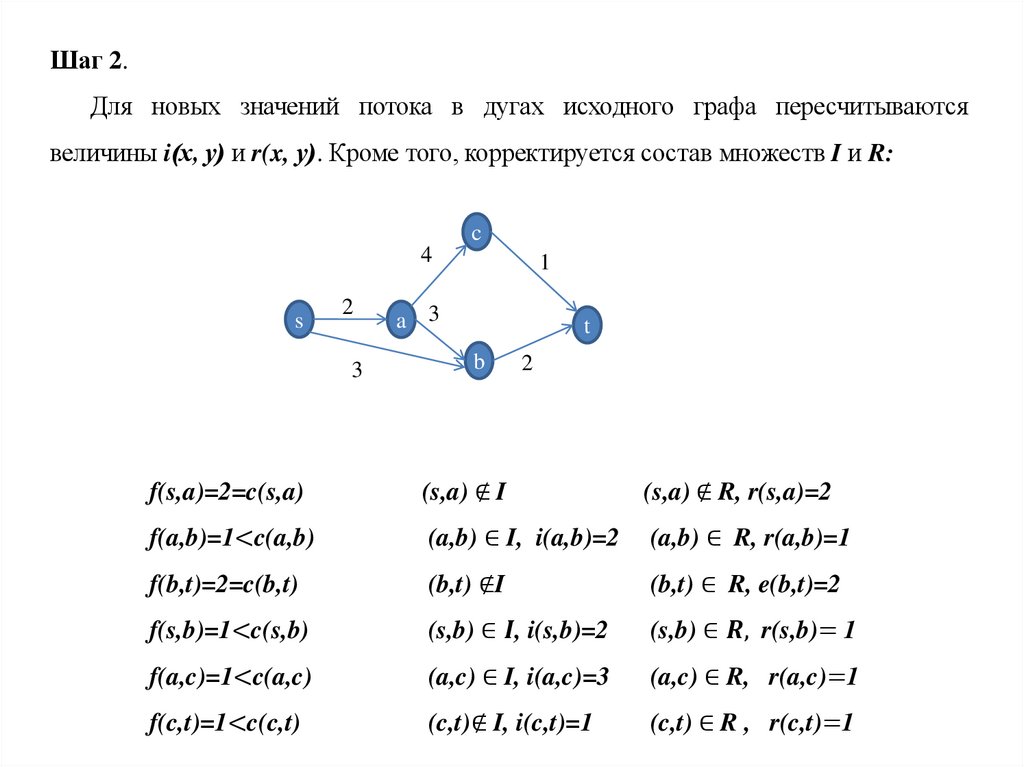
12
Задача о максимальном потоке состоит в поиске способа пересылки
максимального количества единиц потока из источника в сток при условии
отсутствия превышения пропускных способностей дуг исходного графа.
Поток представляет собой любое перемещение соответствующих объектов
из источника s в сток t. Через f(x, у) обозначать количество единиц потока,
прошедших по дуге f(x, у). Для любого потока из s в t количество единиц,
выходящих из любой вершины х (при этом только x≠s, x≠t), должно быть равно
количеству единиц, входящих в эту вершину х, т. е.
σ