Класифікація. Лекція 3

1.

• Лекція 3
Класифікація

2.

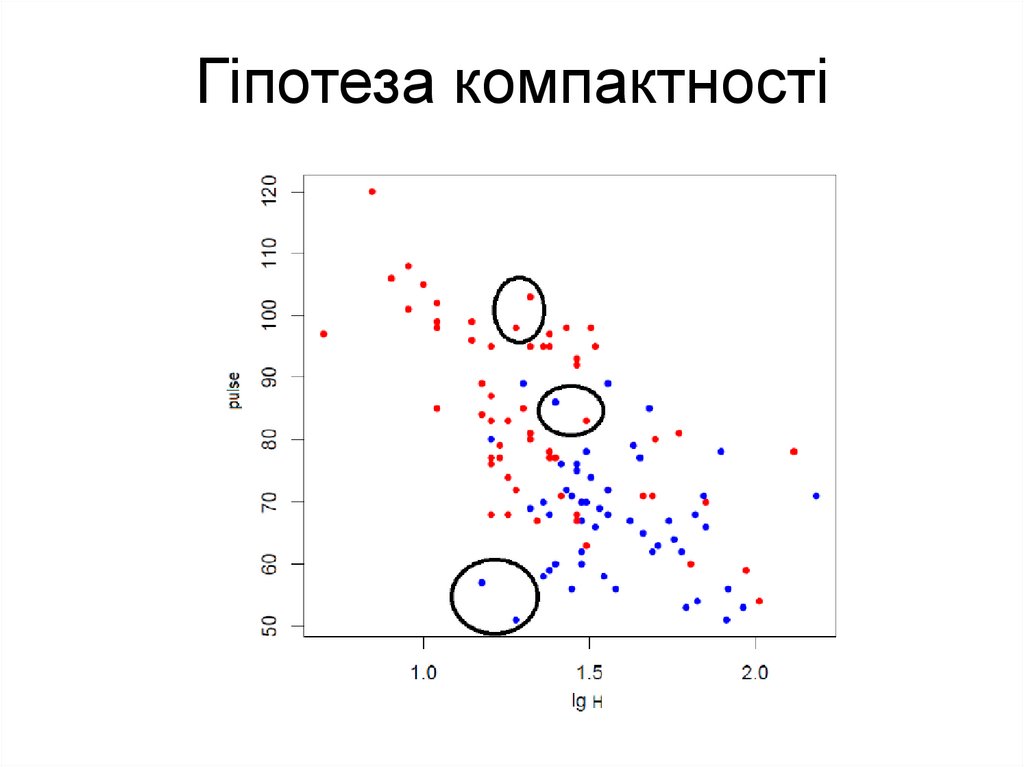
Гіпотези компактності та
безперервності

3.

Гіпотеза компактності

4.

Постановка задачі класифікації
Історично виникла із завдання машинного зору,
тому часто вживаний синонім - розпізнавання образів.
У класичній задачі класифікації навчальна вибірка являє
собою набір окремих об'єктів
,
що характеризуються вектором речовозначних ознак
, змінна,
Як результат об'єкта x фігурує
що набуває значень, зазвичай із множини
Y=
.
Потрібно побудувати алгоритм (класифікатор),
який за вектором ознак x повернув би мітку класу або вектор
оцінок приналежності (апостеріорних імовірностей) до
кожного
з
класів,
що
характеризуються
вектором
речовозначних ознак
.

5.

Метод k найближчих сусідів

6.

Міри близькості

7.

Метод k найближчих сусідів
Вибір k

8.

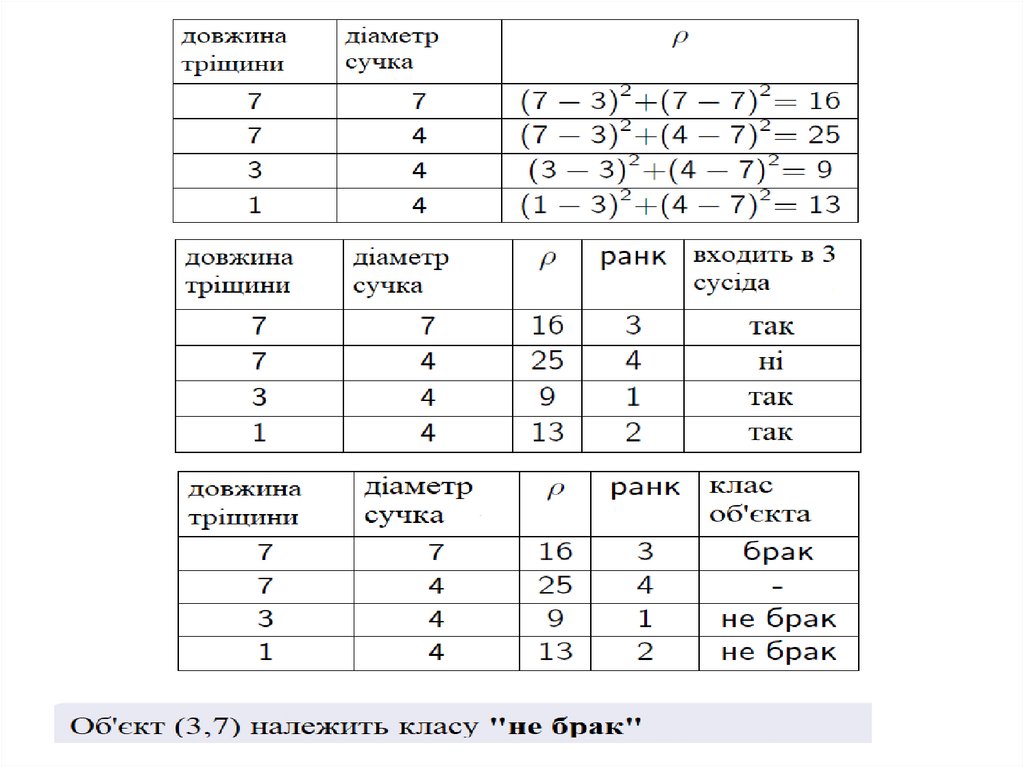
Приклад

9.

10.

1-правило
Алгоритм побудови 1-правил
. Найпростіший алгоритм формування елементарних правил для
класифікації об'єкта. Він будує правила за значенням однієї
незалежної змінної, тому в літературі його часто називають "1правило" (1-rule) або коротко 1R-алгоритм.
. Ідея алгоритму :
Для будь-якої незалежної змінної формується правило, яке класифікує
об'єкти з навчальної вибірки. При цьому вказується значення залежної
змінної, яке найчастіше трапляється в об'єктів з обраним значенням
незалежної змінної. У цьому разі помилкою правила є кількість
об'єктів, що мають те саме значення розглянутої змінної, але не
належать до обраного класу.
. Таким чином, для кожної змінної буде отримано набір правил
(для кожного значення). Оцінивши ступінь помилки кожного
набору, обирають змінну, для якої побудовано правила з
найменшою помилкою.

11.

Example
• Let T be the following table
Office
House
Party
Dem
State
NY
Vote
Yes
House
Dem
NJ
No
House
Dem
CT
Yes
House
Rep
NJ
No
House
Rep
CT
Yes
Senate Dem
NY
No
Senate Dem
NJ
No
Senate Rep
NY
No
Senate Rep
NJ
Yes
Senate Rep
CT
Then BestRule(Vote,Office,T) is "case (X.Office)
{ House: predict (X.Vote==Yes); Senate:
predict(X.Vote==No); }" with an accuracy of 6/10.
Yes
BestRule(Vote,Party,T) is "case (X.Party)
{ Dem: predict (X.Vote==No); Rep:
predict(X.Vote==Yes); }" with an accuracy of 6/10.
BestRule(Vote,State,T) is "case (X.State)
{ NY: predict (X.Vote==No); NJ: predict
(X.Vote==No); CT: predict(X.Vote==Yes) }" with an
accuracy of 8/10.
The 1R algorithm therefore returns
rule голос
Vote the
- виборчий
House - палата NJ:
"case (X.State) { NY: predict (X.Vote==No);
predict (X.Vote==No); CT: predict(X.Vote==Yes) }"
NJ Нью-Джерси
NY Нью-Йорк
CT Коннектикут

12.

. Якщо змінна має дійсний тип, то кількість можливих значень
може бути нескінченною. Для розв'язання цієї проблеми всю
область значень такої змінної розбивають на інтервали таким
чином, щоб кожен із них відповідав певному класу в
навчальній вибірці.
Проблема 1R-алгоритму - це надчутливість (overfitting). Річ у
тім, що алгоритм обиратиме змінні, які приймають найбільшу
кількість можливих значень, оскільки для них помилка буде
найменшою. Наприклад, для змінної, що є ключем (тобто для
кожного об'єкта своє унікальне значення), помилка
дорівнюватиме нулю. Однак для таких змінних правила будуть
абсолютно марними, тому під час формування навчальної
вибірки для цього алгоритму важливо правильно вибрати
незалежних змінних.
. Насамкінець необхідно зазначити, що 1R-алгоритм,
незважаючи на свою простоту, у багатьох випадках на практиці
виявляється досить ефективним. Це пояснюється тим, що
багато об'єктів дійсно можна класифікувати лише за одним
атрибутом. Крім того, нечисленність формованих правил дає
змогу легко зрозуміти й використовувати отримані результати.
.
набір

13.

. Томас Байєс - англійський математик, священник,
член Лондонського королівського товариства.
Автор теореми Байєса - однієї з основних теорем
елементарної теорії ймовірностей.
. Біографія
Байєс народився в Лондоні 1702 року. Його батько
- Джошуа Байєс - був пресвітеріанським
священиком, представником відомого
нонконформістського роду з Шеффілда. Помер
1761 року.
Математичні інтереси Байєса стосувалися теорії
ймовірностей. Він сформулював і розв'язав одну з
основних задач цього розділу математики (теорема
Байєса). Роботу Байєса було опубліковано вже
після його смерті, 1763 року.
За все життя Томас Байєс опублікував лише дві
роботи - одну богословську та одну математичну:
Divine Benevolence, or an Attempt to Prove That the
Principal End of the Divine Providence and Government is
the Happiness of His Creatures (1731г.)
An Introduction to the Doctrine of Fluxions, and a Defence
of the Mathematicians Against the Objections of the
Author of The Analyst (опубликовано анонимно в 1736г.)

14.

Теорема Байєса і класифікація
(1)

15.

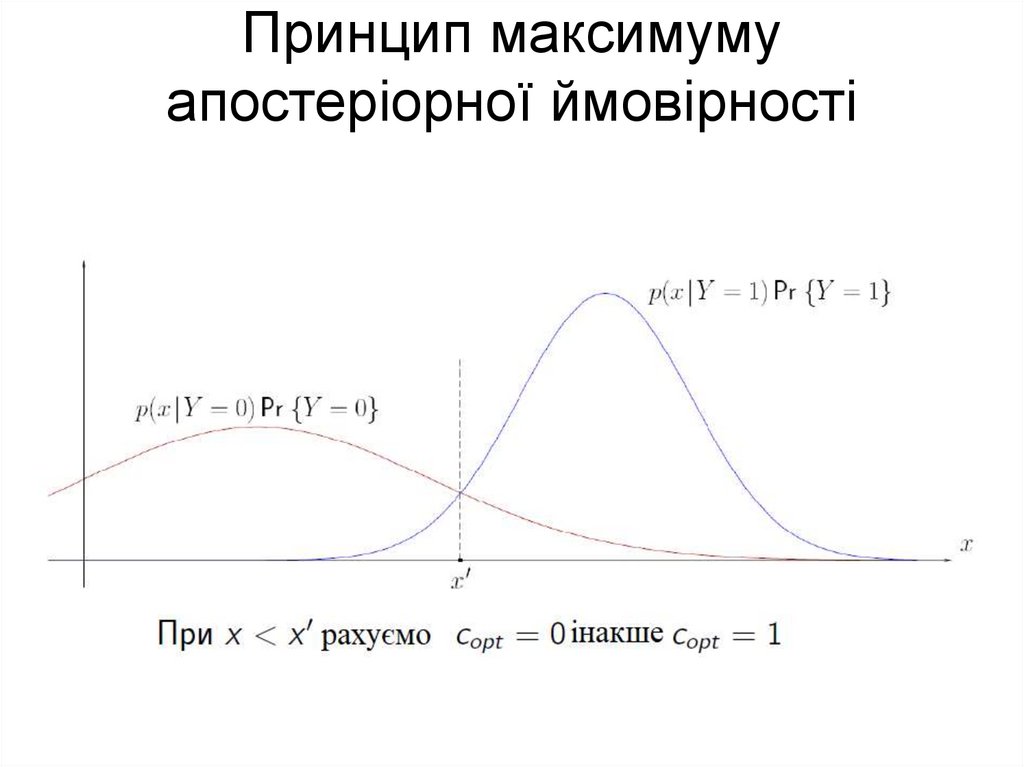
Принцип максимуму
апостеріорної ймовірності

16.

Байесовский классификатор

17.

Наївний байєсівський класифікатор
Naive bayes

18.

Оценка вероятностей в наивном байесовском
классификаторе

19.

20.

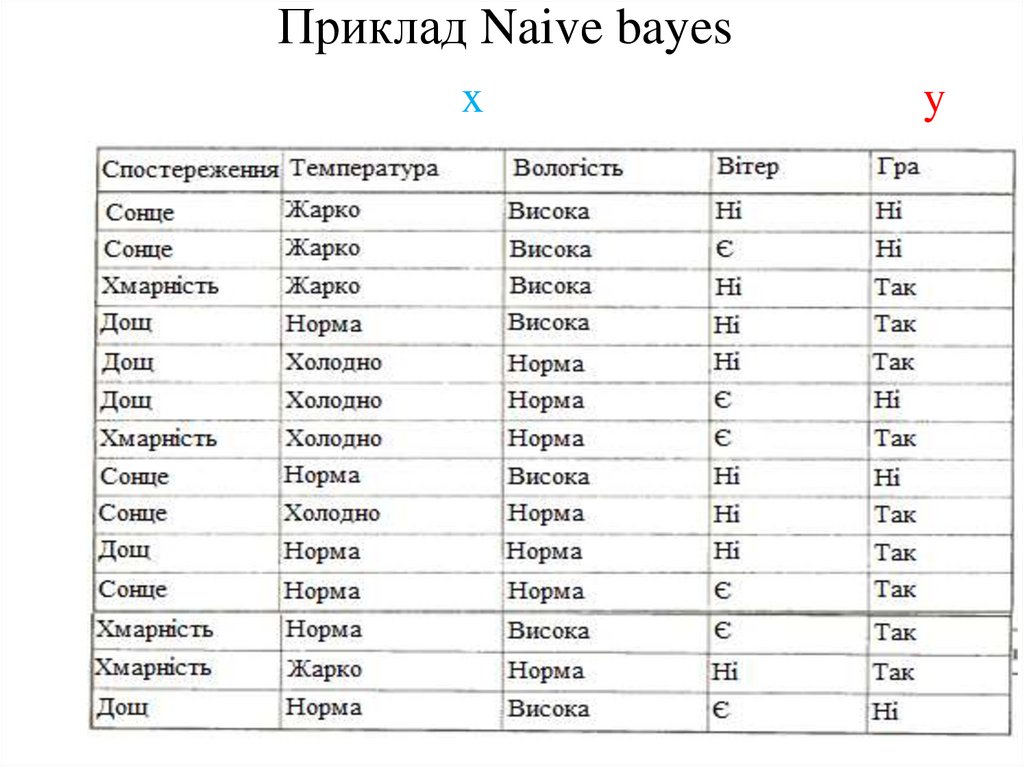
Приклад Naive bayes
x
y
20

21.

Метод Naive bayes.
Необхідно визначити, чи відбудеться гра
за таких значень незалежних змінних
(подія Е):
21

22.

Визначаємо умовні ймовірності

23.

Метод Naive bayes.
P(y cr)
Апріорні Ймовірності
є відношення об'єктів із навчальної
вибірки, що належать класу , до
загальної кількості об'єктів у вибірці. У
цьому прикладі це:
23

24.

Метод Naive bayes.
Обчислимо наступні апостеріорні
ймовірності:
24

25.

Метод Naive bayes.
Підставляючи відповідні ймовірності,
отримаємо такі значення:
Імовірність P(Е )не враховується, оскільки під
час нормалізації ймовірностей для кожного з
можливих правил вона зникає.
Нормалізована ймовірність для правила
обчислюється за формулою:
25
P
(
y
c
|
E
)
P
(
y
c
|
E
)
/
P
(
y
c
|
E
)
r
r
r

26.

Метод Naive bayes.
У цьому випадку можна стверджувати, що за
вказаних умов гра відбудеться з імовірністю:
Р`(гра = так | Е) = 0,0053/ (0,0053+0,0206)=0,205
і не відбудеться з ймовірністю:
Р`(гра = ні | Е) = 0,0206/(0,0053+0,0206)=0,795
Таким чином, за вказаних умов більш
ймовірно, що гра не відбудеться.
26

27.

Використання багатовимірного
нормального розподілу в задачі
розпізнавання образів
.
У
статистичній
теорії
розпізнавання
образів
використовується апроксимація щільності за допомогою
багатовимірного нормального розподілу.
Під час розв'язання задач розпізнавання за допомогою
формули Байєса у формі (1) можуть використовуватися
густини
ймовірності
p1(x),….,pn(x),
в яких змінні X1,…,Xn не обов'язково є незалежними.
Найчастіше використовують багатовимірний нормальний
розподіл. Щільність цього розподілу в загальному вигляді
подається виразом
• де

28.

29.

30.

У результаті вирішальне правило розпізнавання має вигляд
де
У разі лінійного класифікатора
правило набуде вигляду
де
і вирішальне

31.

32.

Лінійний дискримінант Фішера