Similar presentations:
Рекуррентные соотношения и где они обитают
1. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ
и где они обитают2.
История развития ДМ. ЗадачиПринцип Дирихле
Основные правила комбинаторики
Выборки. Комбинаторные числа
Метод включений и исключений
Бином Ньютона. Полиномиальная формула
Рекуррентные соотношения
Производящие функции
3.
Рассмотрим метод рекуррентных соотношений. Онсостоит в том, что решение комбинаторной задачи с n
предметами выражается через решение аналогичной задачи с
меньшим числом предметов с помощью некоторого
соотношения, которое называется рекуррентным (recurrence возвращение). Пользуясь этим соотношением, искомую
величину можно вычислить, исходя из того, что для
небольшого количества предметов (одного, двух) решение
задачи обычно очевидно или легко находится.
4.
5.
Таким образом, установлено рекуррентное соотношениеPn = n∙Pn – 1.
Отсюда получаем:
Pn = n ∙ Pn – 1 = n(n – 1)Pn – 2 = n(n – 1)(n – 2)Pn – 3 = …
= n(n – 1)(n – 2) … 2P1 = n(n – 1)(n – 2) … 2∙1 = n!
6.
Например, выведем формулу для числа перестановок Pn = n!,найдя рекуррентное соотношение, которому удовлетворяет Pn.
Пусть имеется n элементов a1, a2, …, an–1, an. Любую
перестановку этих n элементов можно получить, взяв некоторую
перестановку из n – 1 элемента a1, a2, …, an–1 и присоединив к ней
элемент an. Очевидно, что элемент an может занять любое из n мест.
Поэтому из каждой перестановки элементов a1, a2, …, an–1
получается n перестановок a1, a2, …, an–1, an. Это означает, что
перестановок из n элементов в n раз больше, чем перестановок из n –
1 элемента.
Таким образом, установлено рекуррентное соотношение
Pn = n∙Pn – 1. Отсюда получаем:
Pn = n ∙ Pn – 1 = n(n – 1)Pn – 2 = n(n – 1)(n – 2)Pn – 3 = …
= n(n – 1)(n – 2) … 2P1 = n(n – 1)(n – 2) … 2∙1 = n!
7.
Задача. Сколькими способами можно замостить прямоугольную доскуразмером 2 х 7 костями домино, если все кости считать одинаковыми и
учитывать только положение кости: горизонтальное или вертикальное?
8.
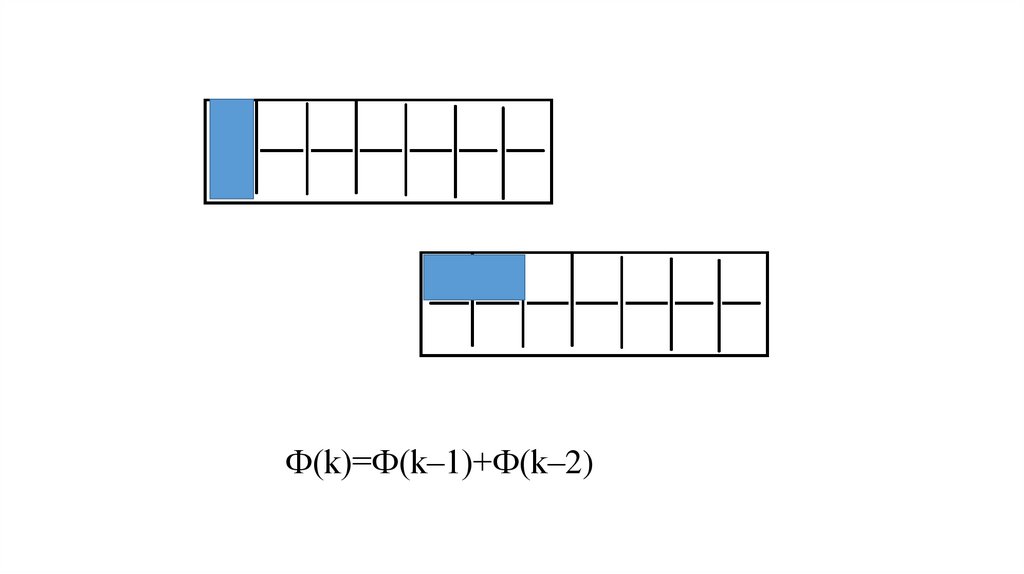
Ф(k)=Ф(k–1)+Ф(k–2)9.
Решение. Обозначим через Ф(k) количество способов замостить костямидомино прямоугольную доску размером 2 х k.
Угловая клетка может быть закрыта одним из двух способов: либо костью,
которая лежит вертикально, тогда оставшуюся k – 1 кость можно положить
Ф(k–1) способами, либо костью, которая лежит горизонтально, тогда еще
одну кость можем положить только горизонтально, а оставшиеся k–2 кости
можно уложить Ф(k–2) способами.
Используя правило суммы, приходим к соотношению Ф(k)=Ф(k–1)+Ф(k–2).
Учитывая, что Ф(0)=Ф(1)=1, можем для любого значения k найти ответ:
Ф(2)=2, Ф(3)=3, Ф(4)=5, Ф(5)=8, Ф(6)=13, Ф(7)=21.
Имеем 21 способ замостить костями домино прямоугольную доску
размером 2 х 7.
10.
11.
Задача. За пересылку заказного письма надо уплатить 18 р.Сколькими способами можно оплатить его марками стоимостью
в 4, 6 и 10 р. (два способа, отличающихся порядком марок,
считаются различными; запас марок не ограничен)?
12.
F(N) = F(N – 4) + F(N – 6) + F(N – 10)13.
Пример2.
За
пересылку
заказного
письма
надо
уплатить
18 р. Сколькими способами можно оплатить его марками стоимостью в 4, 6 и 10 р. (два способа,
отличающихся порядком марок, считаются различными; запас марок не ограничен)?
Решение
Обозначим через F(N) число способов, которыми можно наклеить марки в 4, 6 и 10 р. так, чтобы
общая стоимость этих марок равнялась N.
Для F(N) выполняется рекуррентное соотношение F(N) = F(N – 4) + F(N – 6) + F(N – 10).
Действительно, пусть имеется некоторый способ наклейки марок с общей стоимостью N, и пусть
первой наклеивалась марка стоимостью в 4 р. Тогда все остальные марки стоят N – 4 р.
Если
же
к
любой
комбинации
марок
общей
стоимостью
N – 4 р. присоединить одну марку стоимостью 4 р., то получим комбинацию марок стоимостью в N р.
Следовательно, число комбинаций, когда первой приклеивается марка стоимостью 4 р., равно
F(N – 4).
Аналогично доказывается, что число комбинаций, начинающихся на шестирублевую марку,
равно F(N – 6), а на десятирублевую — F(N – 10).
14.
Так как любая комбинация начинается на одну из марокуказанной стоимости, то по правилу суммы получаем
рекуррентное соотношение F(N) = F(N – 4) + F(N – 6) + F(N – 10).
Применяя его к F(18), получим: F(18) = F(14) + F(12) + F(8).
Применив это же соотношение к каждому слагаемому, и
учитывая, что F(0) = 1, F(1) = F(2) = F(3) = 0, F(4) = 1, F(5) = 0,
F(6) = 1, F(7) = 0, F(8) = 1, F(9) = 0 (сумму в 0 р. можно получить
только одним способом (совсем не наклеивая марок), а суммы в 1,
2, 3, 5, 7 и 9 р. вообще нельзя получить с помощью марок в 4, 6 и
10 р.) получим:
F(18) = F(14) + F(12) + F(8) = (F(10) + F(8) + F(4)) +
(F(8)+F(6) + F(2)) + F(8) = F(10) + 3F(8) + F(6) + F(4) + F(2) =
= F(6) + F(4) + F(0) + 3F(8) + F(6) + F(4) + F(2) = 3F(8) + 2F(6) +
+ 2F(4) + F(2) + F(0) = 3 1 + 2 1 + 2 1 + 0 + 1 = 8.
Таким образом, марки можно наклеить восемью способами.
15.
16.
Пример 3. Абитуриент знает, что для поступления ввуз ему достаточно набрать 17 баллов. Сколькими
способами он может сдать 4 экзамена, чтобы наверняка
поступить в вуз (результат экзамена оценивается 2, 3, 4
или 5 баллами, с оценкой 2 в вуз не принимают)?
17.
18.
РешениеОбозначим через F(k, N) число способов, которыми можно набрать
N баллов после k экзаменов.
Можно доказать, что для F(k, N) выполняется рекуррентное
соотношение:
F(k, N) = F(k – 1, N – 3) + F(k – 1, N – 4) + F(k – 1, N – 5).
19.
Отсюда получаем, что:F(4, 17) = F(3, 14) + F(3, 13) + F(3, 12) = (F(2, 11) + F(2, 10) +
+ F(2, 9)) + (F(2, 10) + F(2, 9) + F(2, 8)) + (F(2, 9) + F(2, 8) +
+ F(2, 7)) = F(2, 11) + 2F(2, 10) + 3F(2, 9) + 2F(2, 8) + F(2, 7).
Так, как набрать 11 баллов после 2 экзаменов невозможно, а набрать 10
баллов можно единственным способом (получив две пятерки), то
F(2, 11) = 0, F(2, 10) = 1. Следовательно, далее имеем:
F(4, 17) = 2 + 3(F(1, 6) + F(1, 5) + F(1, 4)) + 2(F(1, 5) +
+ F(1, 4) + F(1, 3)) + (F(1, 4) + F(1, 3) + F(1, 2)).
Так, как набрать 6 баллов за один экзамен нельзя, а с двойкой в вуз не
принимают, то F(1, 6) = F(1, 2) = 0.
Очевидно, что F(1, 3) = F(1, 4) = F(1, 5) = 1. Окончательно получаем:
F(4, 17) = 2 + 3 (0 + 1 + 1) + 2 (1 + 1 +1) + 1 + 1 + 0 = 16.
Аналогично получаем, что F(4, 18) = 10, F(4, 19) = 4, F(4, 20) = 1.
Число
способов
успешной
сдачи
экзаменов
F(4, 17) + F(4, 18) + F(4, 19) + F(4, 20) = 16 + 10 + 4 + 1 = 31.
равно
20.
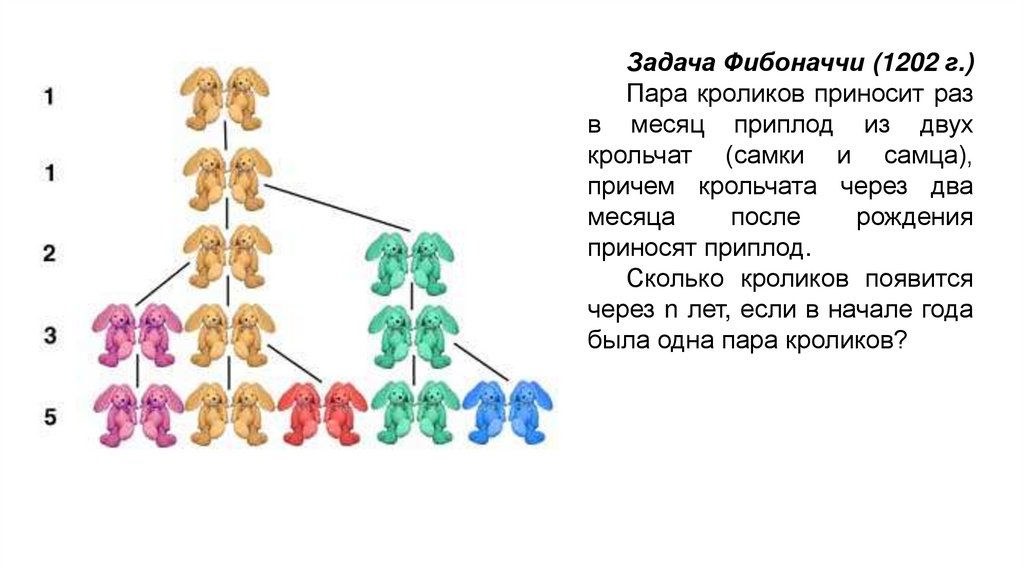
Задача Фибоначчи (1202 г.)Пара кроликов приносит раз
в месяц приплод из двух
крольчат (самки и самца),
причем крольчата через два
месяца
после
рождения
приносят приплод.
Сколько кроликов появится
через n лет, если в начале года
была одна пара кроликов?
21.
22.
23.
24.
25.
26.
27.
28.
29. Задача о прыгуне
Прыгун может прыгать в одном направлении вдольразделенной на клетки полосы, перемещаясь при
каждом прыжке либо в соседнюю клетку, либо через
клетку. Сколькими способами может переместиться из
первой клетки в n-ю? (Способы прыганья считаются
одинаковыми, если в ходе каждого из них прыгун
побывает в одних и тех же клетках).
30.
Обозначим искомое число через Хn.Очевидно Х1=1(переход из первой клетки в первую же осуществляется
только одним способом-отсутствием прыжков) и Х2=1 (переход из первой
клетки во вторую также единствен: он состоит в одном непосредственном
прыжке на соседнюю клетку).
Пусть целью прыгуна является достижение (n+2)-й клетки.
Общее число способов осуществление этой цели в наших обозначениях
равно Хn+2.
Но с самого начала эти способы разбиваются на два класса:
начинающиеся с прыжка во вторую клетку и начинающиеся с прыжка в
третью клетку. Из второй клетки прыгун может переместиться в (n+2)-ю
Хn+1 способами, а из третьей Хn способами.
Таким образом, последовательность чисел Х1, Х2,…, Хn,…удовлетворяет
рекуррентному соотношению: Хn+Хn+1=Хn+2 и поэтому совпадает с
последовательностью чисел Фибоначчи.
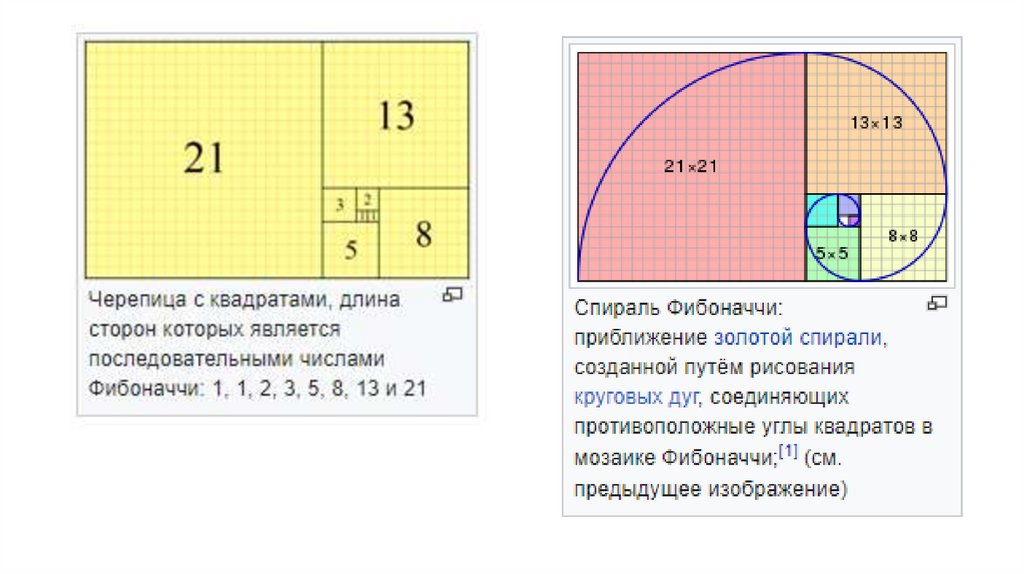
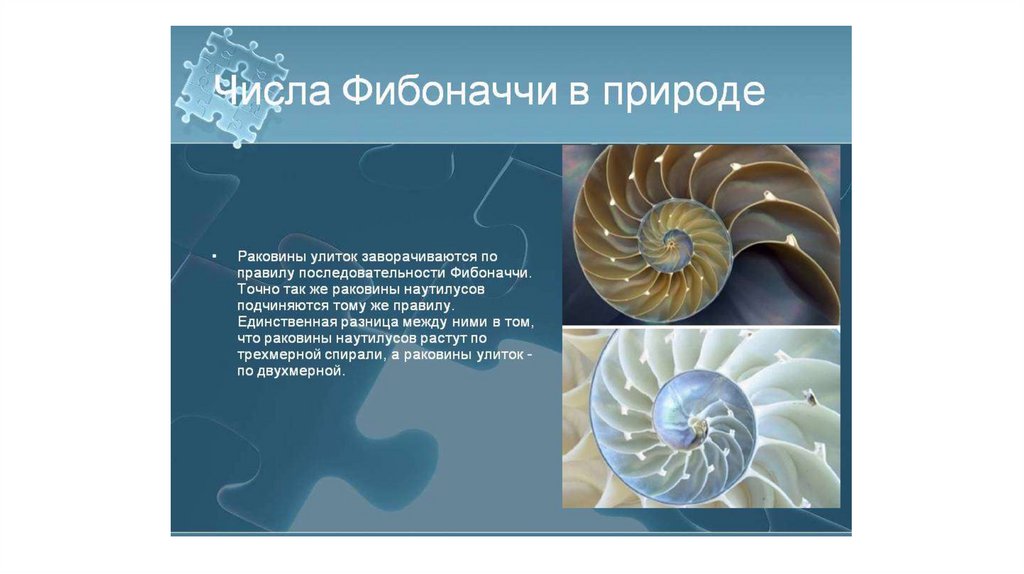
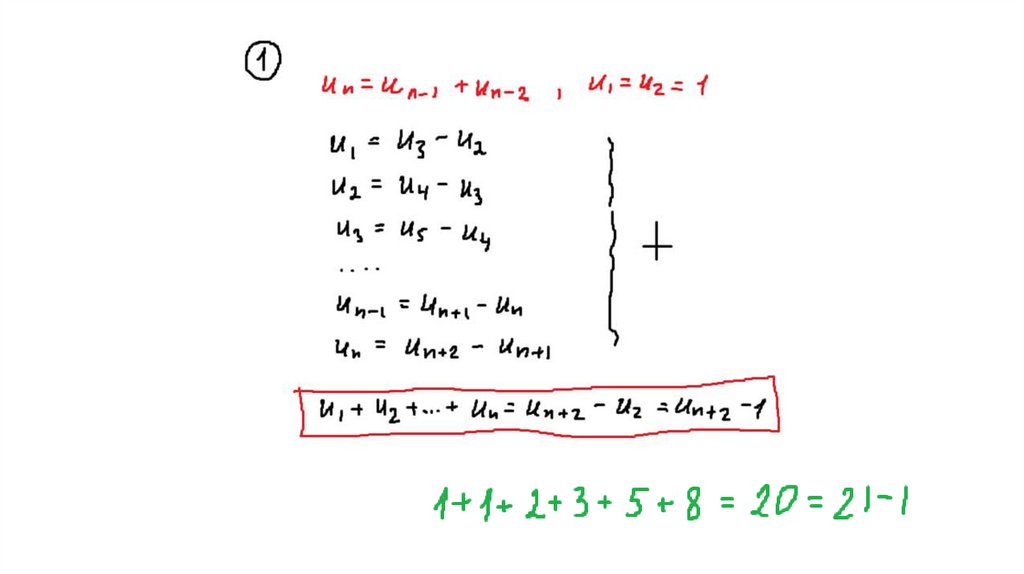
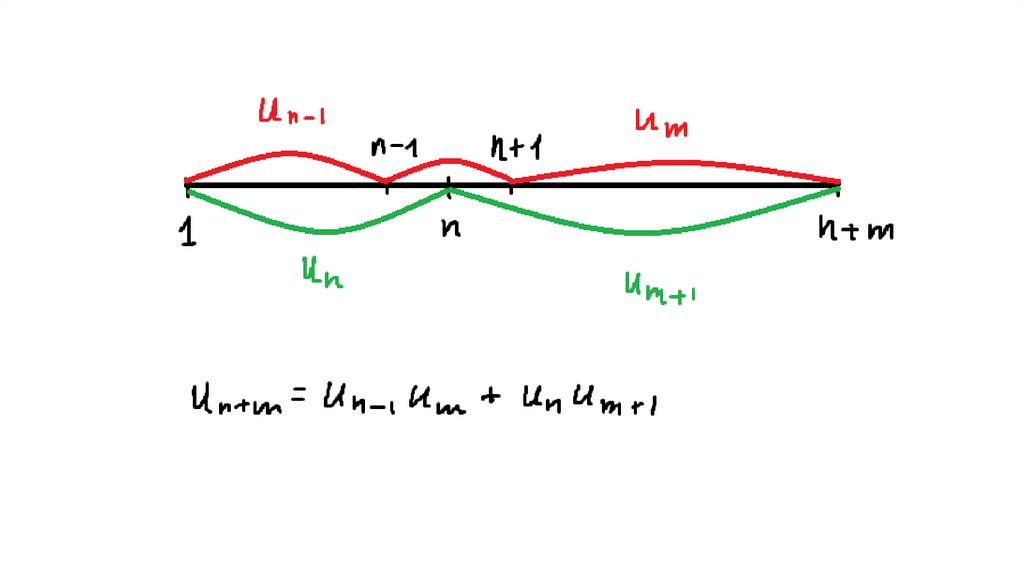
31. Свойства чисел Фибоначчи
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43. Числа Люка L0 = 1, L1 = 3, Ln+1 = Ln + Ln-1 Ln = Fn-1 + Fn+1
44. Разбиение чисел на слагаемые
Обобщение задачи о маркахОбщая постановка задачи
Раскладка предметов в ящики
45. 5=5 4+1 1+4 3+2 2+3
5=3+1+11+3+1
1+1+3
2+2+1
2+1+2
1+2+2
5=2+1+1+1
1+2+1+1
1+1+2+1
1+1+1+2
1+1+1+1+1
5=2+2+1
11+11+1
46. На сколько частей делят плоскость n прямых?
47.
48.
Определение. Последовательность a0, a1, a2, … называют рекуррентной,если указана зависимость общего члена последовательности от предыдущих и
заданы значения необходимого числа начальных членов последовательности.
Саму зависимость иногда называют рекуррентностью.
Определение. Рекуррентным соотношением, или рекуррентной
формулой, называют соотношение вида an+k = F(n, an, an+1, …, an+k – 1), которое
позволяет вычислять любой член последовательности, если заданы её первые k
членов.
Замечание. Иногда вместо an пишут a(n).
49.
Определение. Последовательность называется решениемрекуррентного соотношения, если при подстановке этой
последовательности рекуррентное соотношение тождественно
выполняется.
Пример.
Решением
рекуррентного
соотношения
an + 2 = 3an + 1 – 2an является последовательность 2, 4, 8, …, 2n,…,
т.е. an = 2n.
Действительно, имеем an + 2 = 2n + 2; an + 1 = 2n + 1.
Подставляя эти выражения в рекуррентное соотношение,
получаем
2n + 2 = 3 ∙ 2n + 1 – 2 ∙ 2n; 2n + 2 = 3 ∙ 2n + 1 – 2n + 1; 2n + 2 = 2 ∙ 2n + 1;
2n + 2 = 2n + 2.
50.
Определение. Рекуррентное соотношение имеет порядок k,если оно позволяет выразить f(n + k) через f(n), f(n + 1), …,
f(n + k–1).
Например,
f(n + 2) = f(n) ∙ f(n + 1) – 3f 2(n + 1) + 1 –
рекуррентное соотношение второго порядка;
f(n + 3) = 6f(n) ∙ f(n + 2) + f(n + 1) –
рекуррентное соотношение третьего порядка.
51.
Если задано рекуррентное соотношение k-го порядка безначальных условий, то ему удовлетворяет бесконечно много
последовательностей,
так
как
первые
k
членов
последовательности можно задать совершенно произвольно —
между ними нет никаких соотношений.
Но если первые k членов последовательности заданы, то
все остальные члены последовательности определяются
однозначно. Пользуясь рекуррентным соотношением и
начальными членами, можно один за другим выписывать
члены последовательности, и рано или поздно мы получим
любой её член.
Однако в некоторых случаях необходим определенный
член последовательности, и предыдущие члены (а их может
быть очень много) не нужны. В этих случаях удобнее иметь
явную формулу для n-го члена последовательности.
52.
Определение.Общим
решением
рекуррентного
соотношения k-го порядка называется решение, зависящее от k
произвольных постоянных c1, c2, …, ck, такое, что подбором этих
постоянных можно получить любое решение данного
соотношения.
Пример.
Для
рекуррентного
соотношения
f(n + 2) = 5f(n + 1) – 6f(n) общим решением будет
f(n)= c1 ∙ 2n +c2 ∙ 3n.
Действительно, подставляя его в рекуррентное соотношение,
получаем:
c1 ∙ 2n + 2 + c2 ∙ 3n + 2 = 5(c1 ∙ 2n + 1 + c2 ∙ 3n + 1) – 6(c1 ∙ 2n + c2 ∙ 3n);
4c1 ∙ 2n + 9c2 ∙ 3n = 10c1 ∙ 2n + 15c2 ∙ 3n – 6c1 ∙ 2n – 6c2 ∙ 3n;
4c1 ∙ 2n + 9c2 ∙ 3n = 4c1 ∙ 2n + 9c2 ∙ 3n.
53.
Покажем, что любое решение можно представить в видеf(n) = c1 ∙ 2n + c2 ∙ 3n.
Любое решение рекуррентного соотношения второго порядка
определяется значениями f(1) и f(2). Поэтому нужно доказать, что
для любых f(1) и f(2) найдутся такие значения c1 и c2, что
2c1 3c2 f (1)
4c1 9c2 f (2).
А так как
2 3
0
4 9
то эта система имеет решение при любых c1 и c2.
54.
Для решения рекуррентных соотношений общих методов несуществует.
Основные методы анализа РС:
метод подстановки;
метод, основанный на решении характеристического уравнения.
Метод подстановки заключается в установлении явного выражения
для f(n) и последующем доказательстве для всех n. Для этого выражаем
каждый очередной член последовательности через предыдущие, пока
не станет возможным установить формулу для f(n). Полученную
формулу необходимо доказать (например, методом МИ).
Метод, основанный на решении характеристического уравнения,
применяется для решения линейных рекуррентных соотношений с
постоянными коэффициентами.
55. Пример
Доказать, что56.
ЛИНЕЙНЫЕ ОДНОРОДНЫЕРЕКУРРЕНТНЫЕ
СООТНОШЕНИЯ С
ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
57.
Существует общий метод для решения линейныхрекуррентных
соотношений
с
постоянными
коэффициентами, т.е. для рекуррентных соотношений вида:
f(n + k) = a1 ∙ f(n + k – 1) + a2 ∙ f(n + k – 2) + … + ak ∙ f(n),
где a1, a2, …, ak — постоянные коэффициенты.
58.
Рассмотрим этот метод для линейных рекуррентныхсоотношений с постоянными коэффициентами второго
порядка, т.е. при k = 2;
рекуррентное соотношение при этом имеет вид:
f(n + 2) = a1 ∙ f(n + 1) + a2 ∙ f(n).
Решение этих соотношений основано на следующих
двух утверждениях:
59.
Лемма 1. Если f1(n) и f2(n) являются решениямирекуррентного соотношения f(n + 2) = a1 ∙ f(n + 1) + a2 ∙ f(n), то
при любых A и B, A ∙ f1(n) + B ∙ f2(n) также является решением
этого соотношения.
60.
61.
62.
Из этих двух лемм вытекает следующая теорема,предоставляющая правило решения ЛРСПК 2 порядка.
Теорема. Пусть дано рекуррентное соотношение
f(n + 2) = a1 ∙ f(n + 1) + a2 ∙ f(n).
Составим характеристическое уравнение (квадратное)
t2 = a1∙t + a2
Если это уравнение имеет два различных корня t1 и t2, то
общее решение имеет вид
n 1
n 1
f (n) c1 t 1 c 2 t 2
63.
Пример. Найти общее решение рекуррентного соотношенияf(n + 2) = 15f(n + 1) – 56f(n).
Решение
Соответствующее квадратное уравнение имеет вид
t2 = 15t – 56. Это уравнение имеет два различных корня t1 = 7 и
t2 = 8, следовательно, общее решение этого рекуррентного
соотношения имеет вид
f (n) c1 7
n 1
n 1
c2 8
64.
Пример.Числа
Фибоначчи
задаются
рекуррентным
соотношением F(n + 1) = F(n) + F(n – 1).
Найти общее решение этого рекуррентного соотношения,
а также решение, удовлетворяющее условиям F(0) = 1; F(1) = 1.









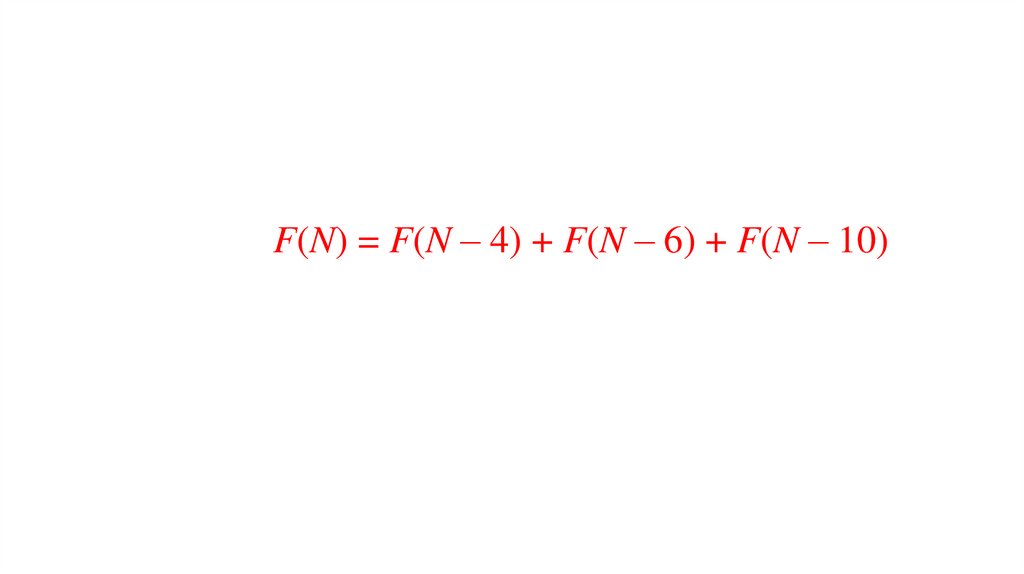


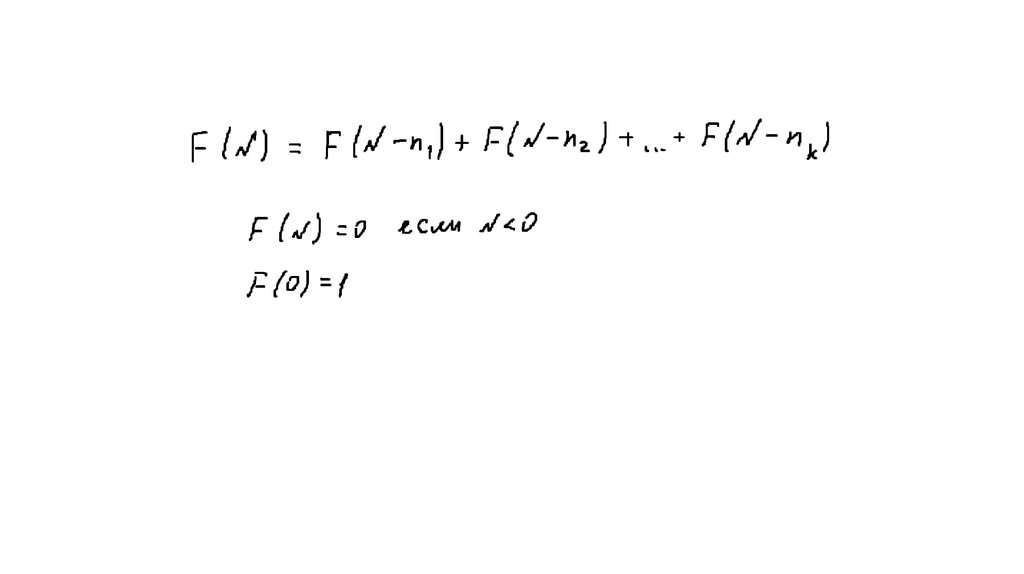

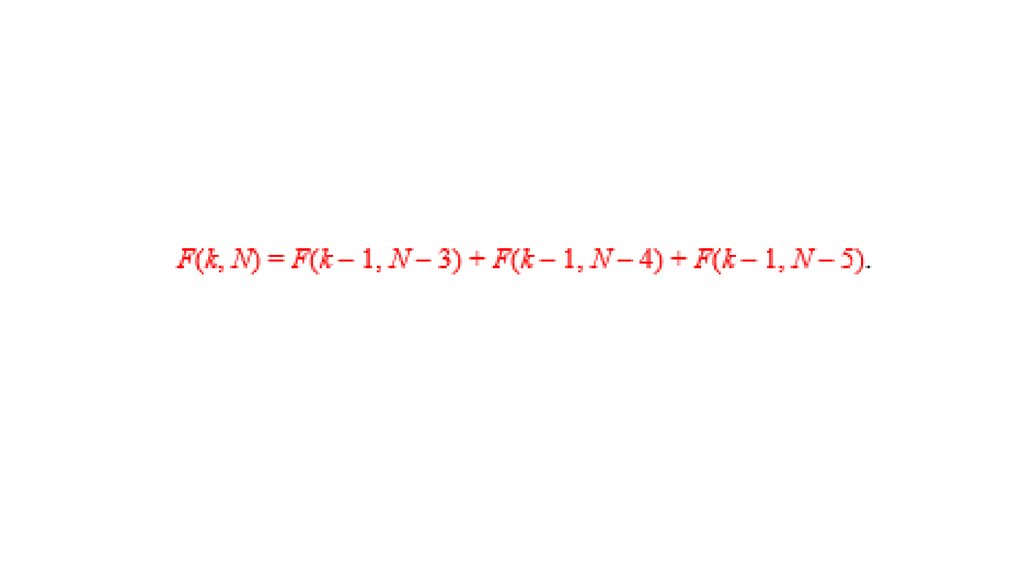












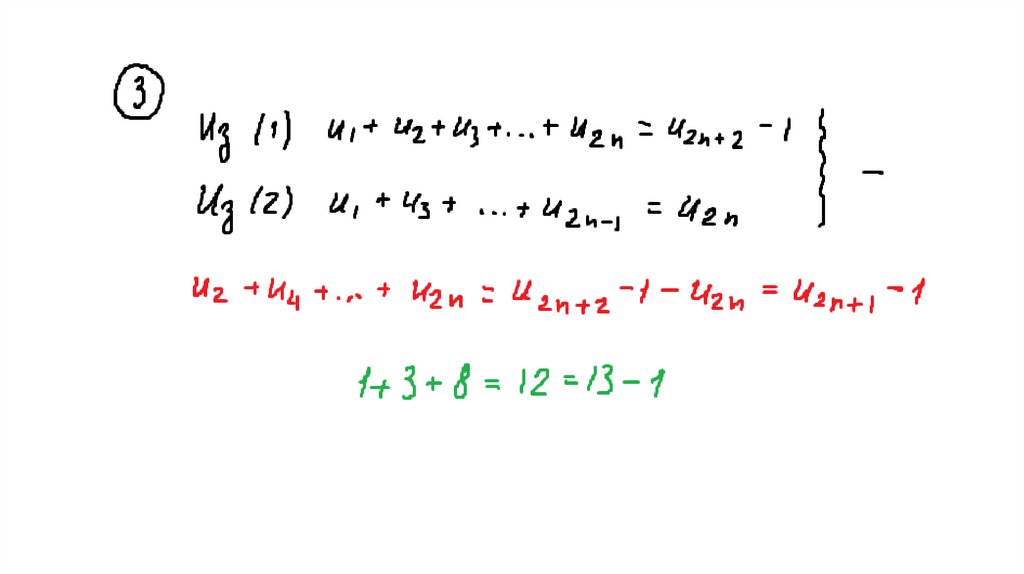
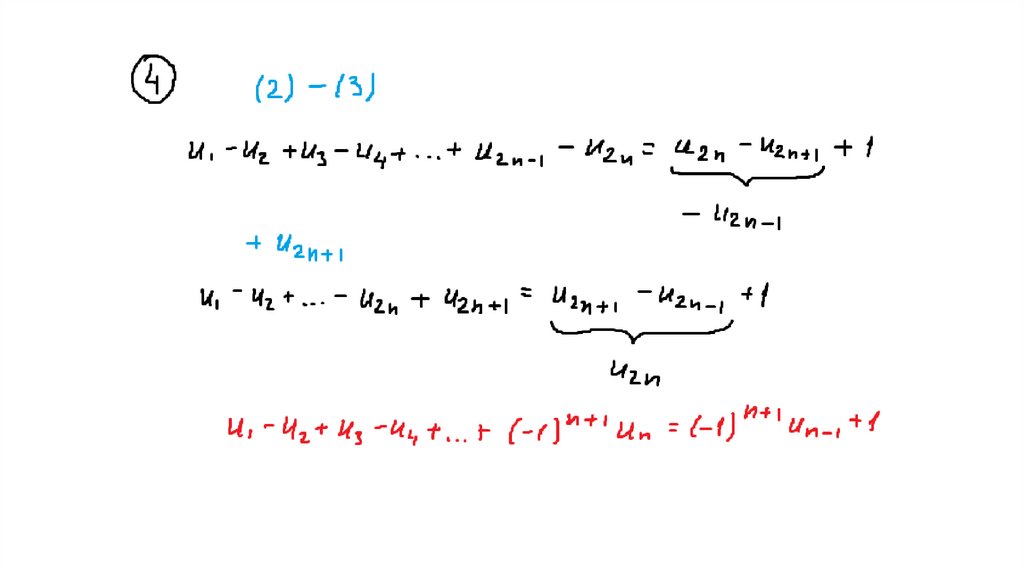
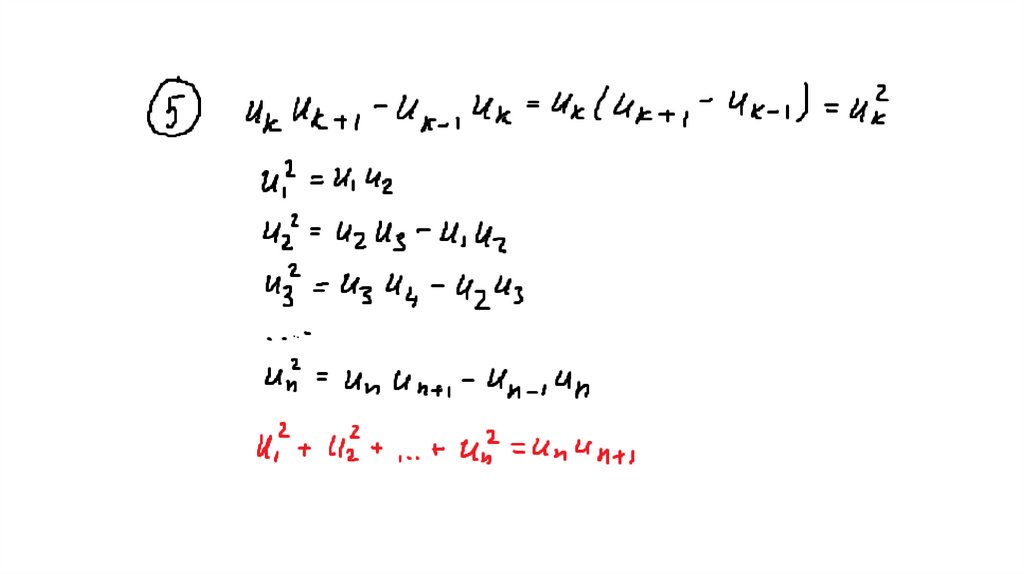
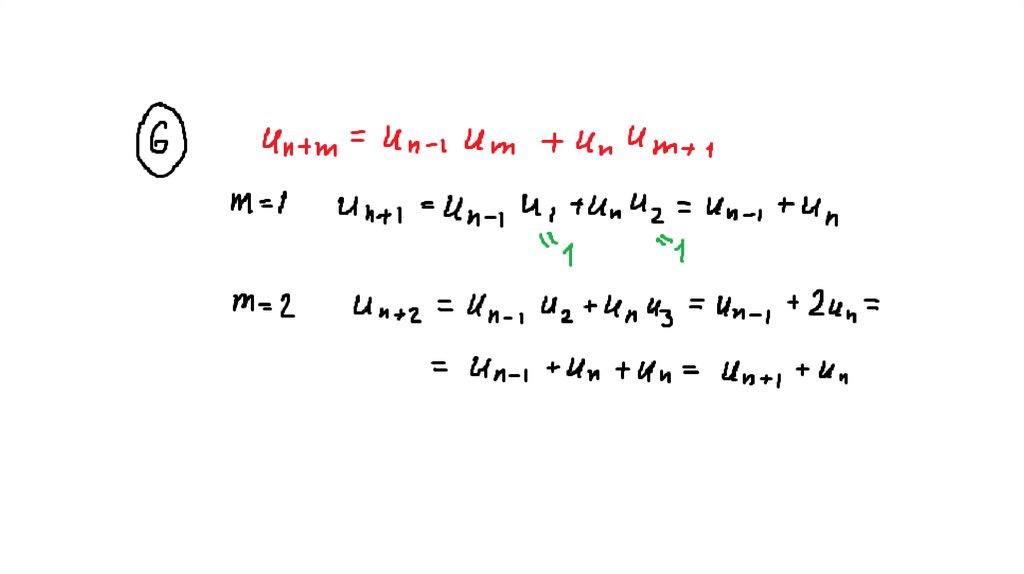


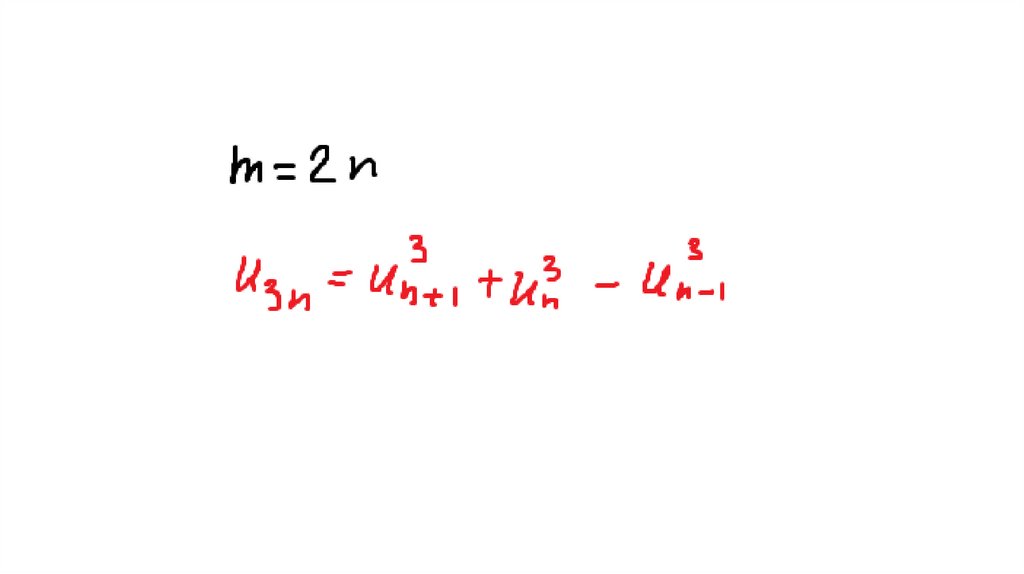

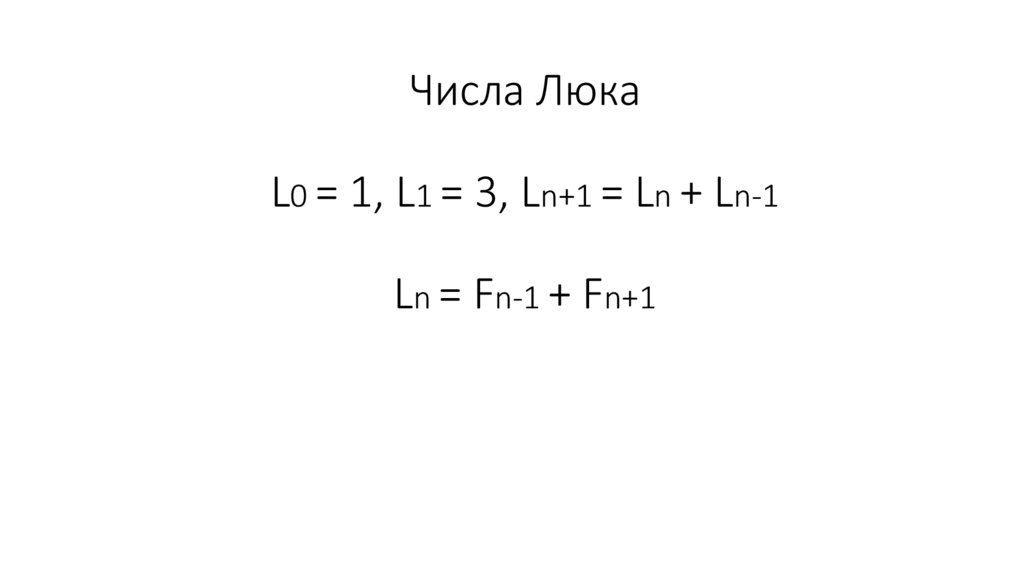











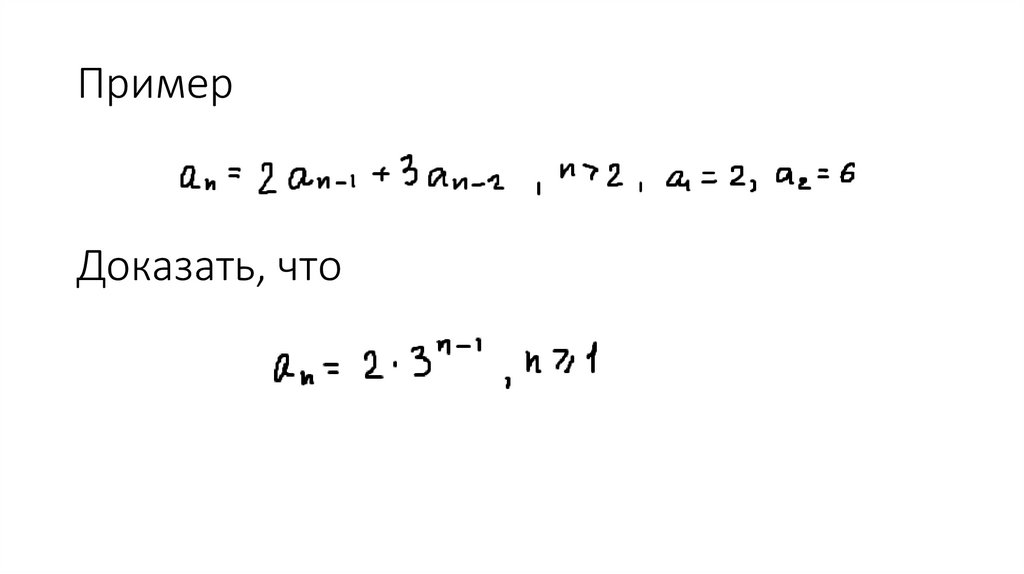











 informatics
informatics








