Применение множества Парето для выбора оптимальных параметров сложных систем

1.

Левичев Александр Сергеевич
Применение множества Парето для выбора
оптимальных параметров сложных систем
Выпускная квалификационная работа
Научный руководитель: к.ф-м.н., доцент Е.Ю.Ечкина
Москва, 2025

2.

Актуал ь ность и проблематика
Сложность систем
Современный мир характеризуется стремительным ростом сложности систем в разных сферах деятельности.
Гонка за процентами эффективности
Если есть возможность что-то хоть чуть-чуть улучшить, то непременно найдётся конкурент, который так и сделает.
Требуется постоянный пересмотр существующих решений.
Цифровизация
Количество данных растёт с каждым днём, всё больше предприятий подвергаются цифровизации.
Смысл
Оптимизация одного критерия часто бессмысленна, т.к. не учитывает множество других важных параметров.
А задача оптимизации нескольких конфликтующих критериев уже требует изобретения специфических
подходов.

3.

Методология оптимизации по Парето и этапы решения
задачи
Решение Б будем называть доминирующим над А, если Б по всем критериям не хуже, а хотя бы по одному лучше, чем А.
Множество решений, над которыми никто не доминирует называется множеством Парето (или Парето-фронтом)
Постановка задачи
Определение целевых критериев и ограничений
Определение типа задачи и выбор алгоритма
Задачи могут быть статические и динамические
Выделение Парето-фронта
Применение алгоритма к данным
Результаты
Анализ параметров или самих оптимальных решений

4.

Плюсы , минусы , подводны е камни
Гибкость применения. К любой задаче максимизации/минимизации
Сужение пространства поиска. Анализ только лучших решений
Прозрачность и наглядность. Однозначные методы выявления лучших. Если решение недоминируемо, то оно
недоминируемо.
Объективность выявления оптимумов. Изначально (без введения коэффициентов или ограничений) непредвзято
выделяются даже заведомо непригодные оптимумы.
Сложность. Для четырёх и более критериев задача вычислительно затратна для больших данных
Несамостоятельность. Оптимальные решения по определению несравнимы между собой
Ошибка выжившего. Пропуски данных в распределениях критериев могут критически влиять на картину оптимальных
решений

5.

Испол ь зованны е материал ы
Of Finding the Maxima of a Set of Vectors, H.T. Kung, F. Luccio, F.P. Preparata
Journal of the Association for Computing Machinery. October 1975, [https://dl.acm.org/doi/pdf/10.1145/321906.321910]
A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II
2002. Kalyanmoy Deb, Amrit Pratap, Sameer Agarwal, T. Meyarivan.
[https://sci2s.ugr.es/sites/default/files/files/Teaching/OtherPostGraduateCourses/Metaheuristicas/Deb_NSGAII.pdf]
Luke S. Essentials of Metaheuristics. A Set of Undergraduate Lecture Notes. Zeroth Edition
Online Version 0.5. October, 2009. Перевод – Юрий Цой. [https://qai.narod.ru/GA/meta-heuristics_7.pdf]
Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts
2014. Wilfried Jakob, Christian Blume. [https://www.mdpi.com/1999-4893/7/1/166]
NSGA II: Non-Dominated Sorting Genetic Algorithm II.
[https://www.thearmchaircritic.org/mansplainings/nsga-ii-non-dominated-sorting-genetic-algorithm-ii]

6.

Испол ь зованны е материал ы
Optimizing fairness and accuracy: a Pareto optimal approach for decision-making
2024. Rashmi Nagpal, Rasoul Shahsavarifar, Vaibhav Goyal, Amar Gupta1. [https://link.springer.com/article/10.1007/s43681024-00508-4]
Построение компромиссных решений и определение эффективности Парето в многокритериальных системах
[https://habr.com/ru/companies/otus/articles/750038]
Модели и методы проактивной поддержки принятия решений при управлении техническим состоянием
оборудования
2020, Сай Ван Квонг
Разработка структуры данных для инкрементальной недоминирующей сортировки
2015, Якупов И.Ю.

7.

Цел ь и составл яющая работы
Цель - разработка применений множества Парето в промышленности для выявления аномалий, предиктивного анализа,
определения оптимальных и критических параметров.
Статический подход
Динамический подход
Получение данных, постановка задачи, формирование
Получение и обработка данных, формирование критериев,
признаков, обучение модели машинного обучения,
решение задачи линейного программирования.
обработка результатов и оценка. Применение генетического
Определение задач и их решение, анализ результатов,
алгоритма для выявления оптимумов и их параметров.
мотивация перехода к динамическому анализу.

8.

Алгоритмы
Полный перебор и алгоритм Кунга
Непосредственное определение недоминируемых решений. Алгоритм Кунга предполагает сортировку по одному из
критериев и последующий отбор по остальным.
Взвешенная сумма критериев и ограничения критериев
Упрощение задачи и уменьшение количества критериев. Детальное исследование Парето-фронта.
NSGA-II
Генетический алгоритм. Формирование случайной популяции, отбор по степени доминируемости и по
разнообразию. Формирование потомков.

9.

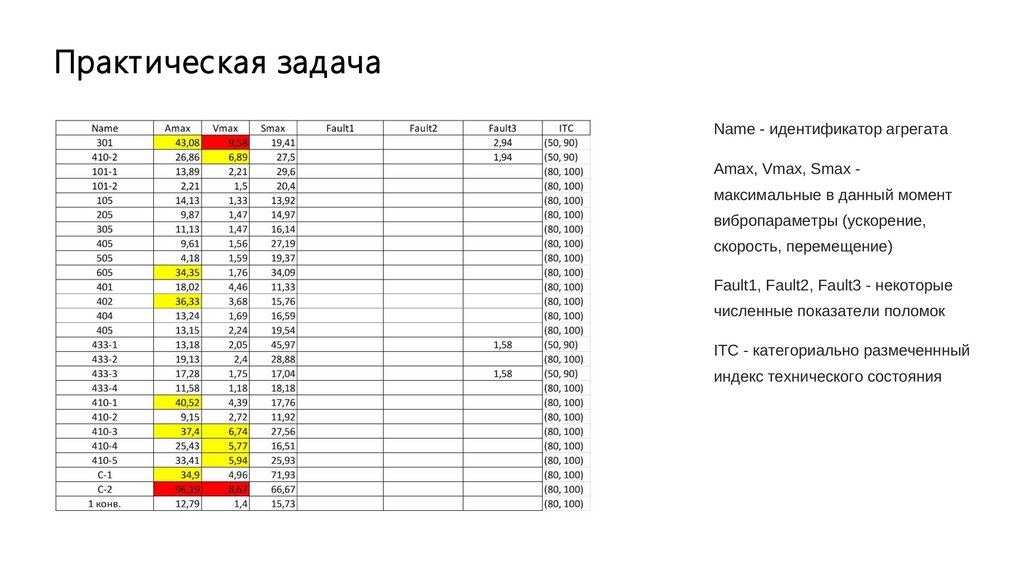
Практическая задача
Name - идентификатор агрегата
Amax, Vmax, Smax максимальные в данный момент
вибропараметры (ускорение,
скорость, перемещение)
Fault1, Fault2, Fault3 - некоторые
численные показатели поломок
ITC - категориально размеченнный
индекс технического состояния

10.

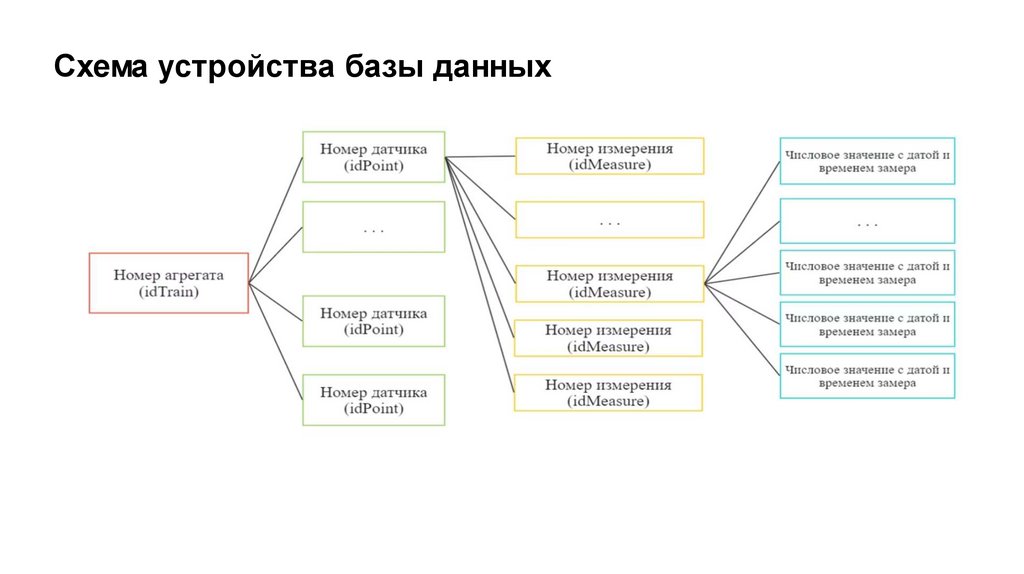
Схема устройства базы данных

11.

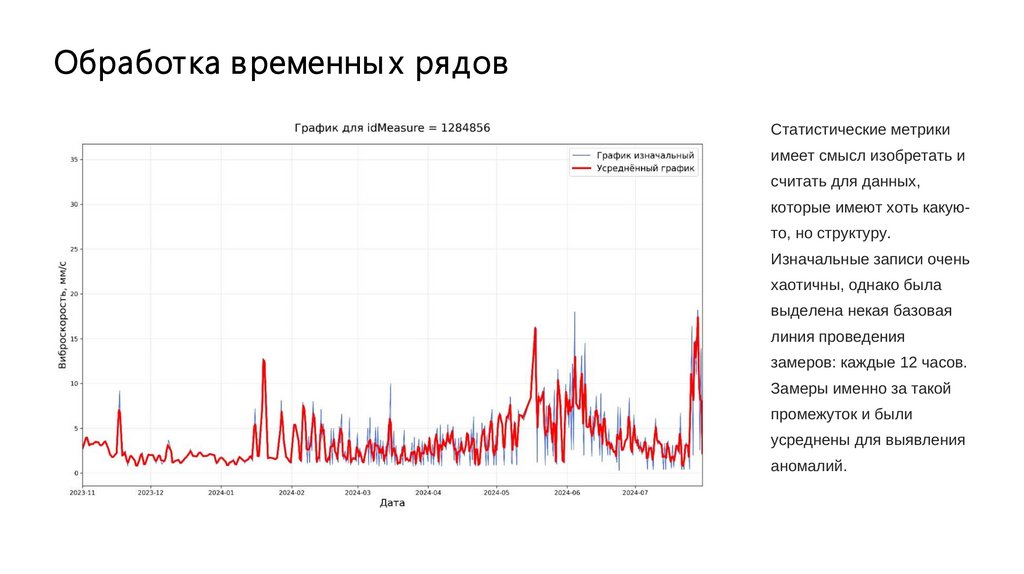
Обработка в ременны х рядов
Статистические метрики
имеет смысл изобретать и
считать для данных,
которые имеют хоть какуюто, но структуру.
Изначальные записи очень
хаотичны, однако была
выделена некая базовая
линия проведения
замеров: каждые 12 часов.
Замеры именно за такой
промежуток и были
усреднены для выявления
аномалий.

12.

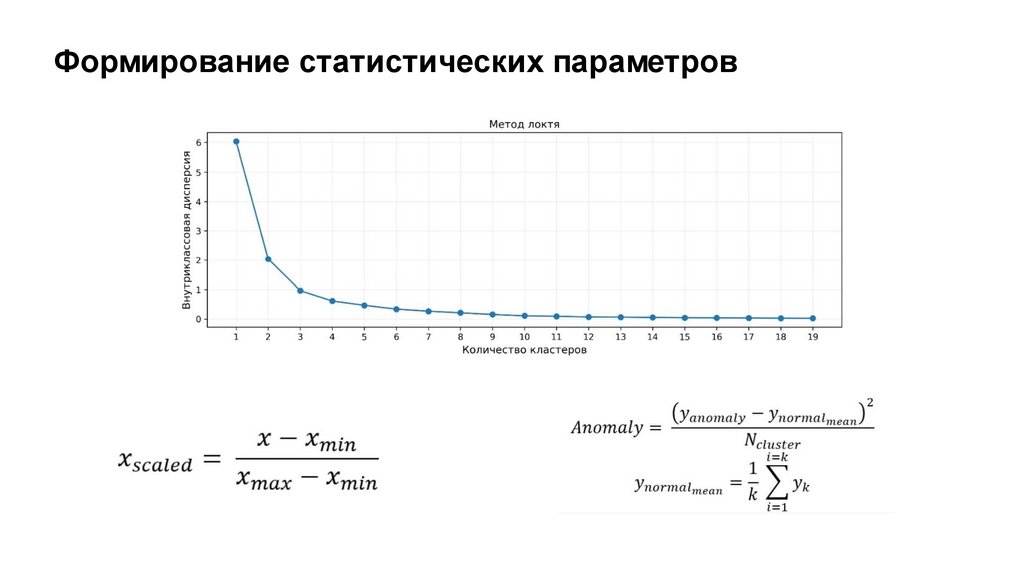
Формирование статистических параметров

13.

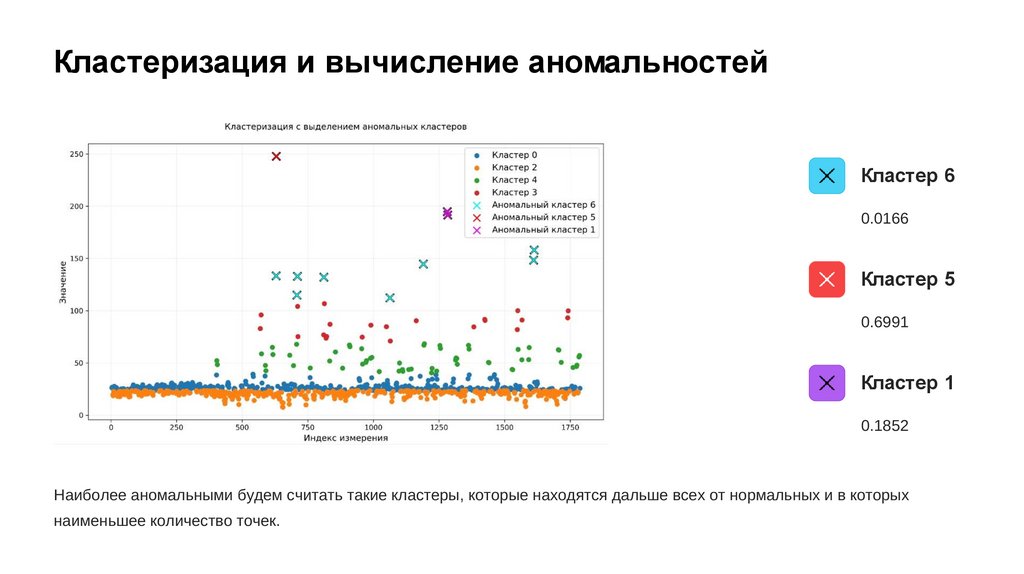
Кластеризация и вычисление аномальностей
Кластер 6
0.0166
Кластер 5
0.6991
Кластер 1
0.1852
Наиболее аномальными будем считать такие кластеры, которые находятся дальше всех от нормальных и в которых
наименьшее количество точек.

14.

Данны е дл я задачи л инейного программирования
Без дополнительных данных
задача линейного
программирования с заданными
ограничениями не решается. Для
каждой точки агрегата и каждой
величины вычислены среднее
значение, дисперсия и
статистическая аномальность.

15.

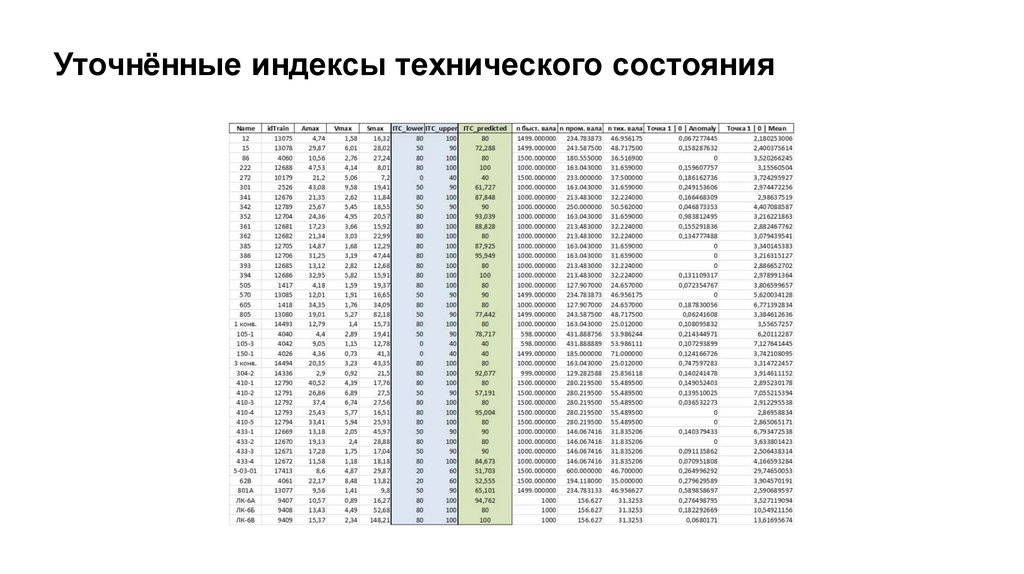
Уточнённые индексы технического состояния

16.

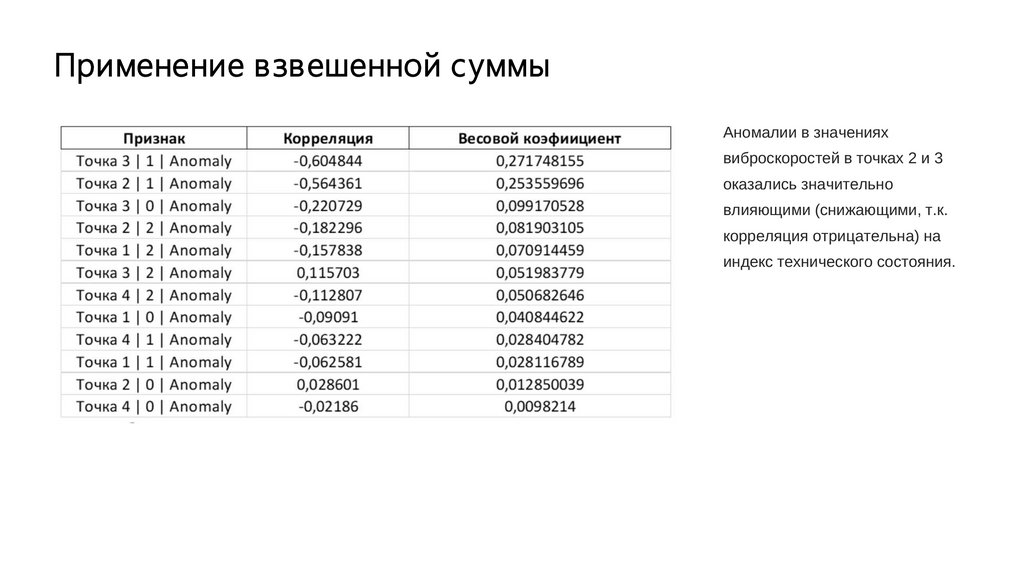
Применение взвешенной суммы
Аномалии в значениях
виброскоростей в точках 2 и 3
оказались значительно
влияющими (снижающими, т.к.
корреляция отрицательна) на
индекс технического состояния.

17.

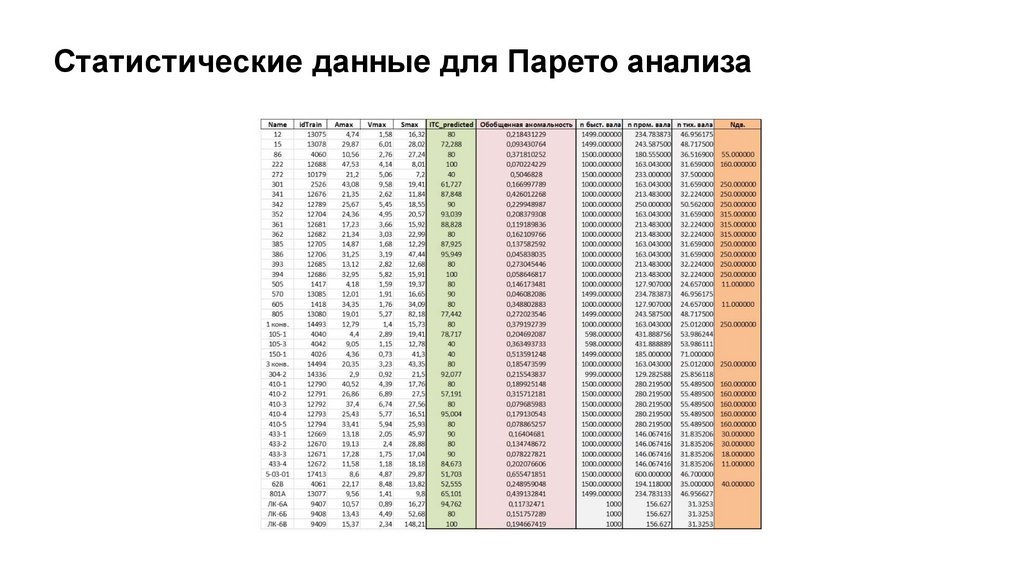
Статистические данные для Парето анализа

18.

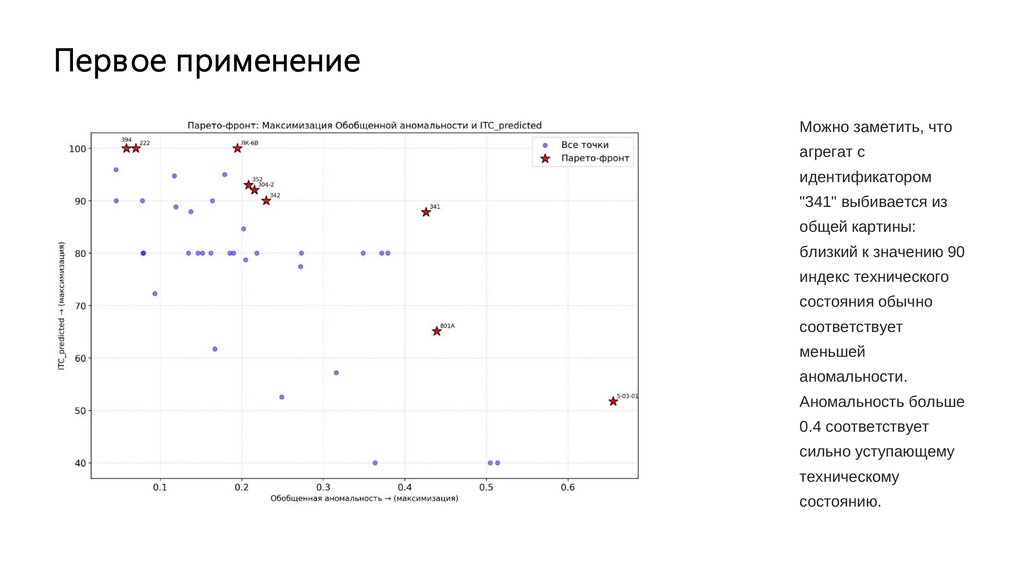
Первое применение
Можно заметить, что
агрегат с
идентификатором
"341" выбивается из
общей картины:
близкий к значению 90
индекс технического
состояния обычно
соответствует
меньшей
аномальности.
Аномальность больше
0.4 соответствует
сильно уступающему
техническому
состоянию.

19.

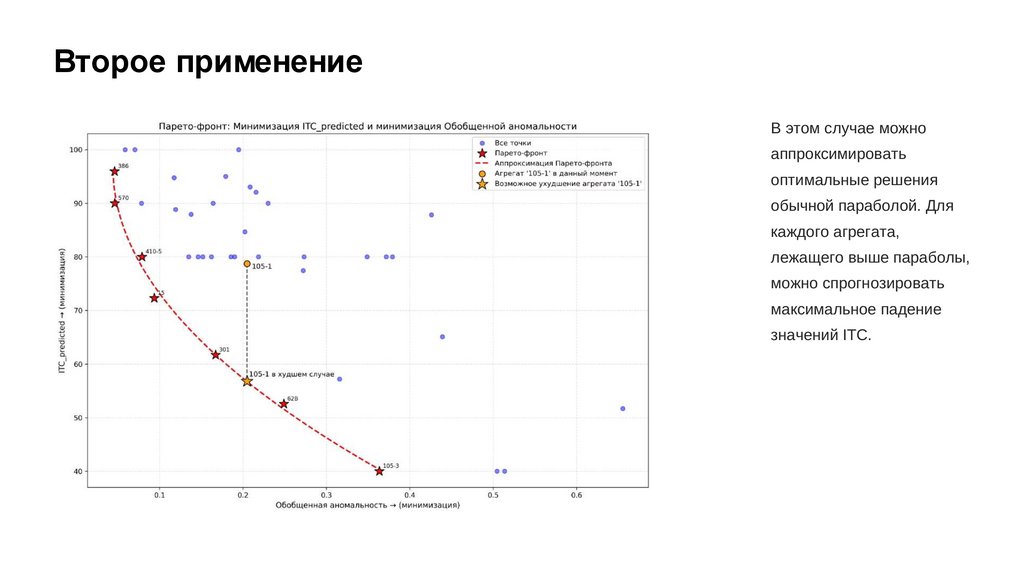
Второе применение
В этом случае можно
аппроксимировать
оптимальные решения
обычной параболой. Для
каждого агрегата,
лежащего выше параболы,
можно спрогнозировать
максимальное падение
значений ITC.

20.

Конец?
Выявлять особенности распределений
четырех параметров (частот валов и
мощности) и их взаимосвязи
представляется сомнительной задачей,
т.к. в Парето фронте оказалось всего 7
решений, тем более, когда имеются
много совпадающих по параметрам
агрегатов.
Если с достаточной точностью
научиться моделировать поведение
агрегатов, можно не просто выявить
реальные оптимальные параметры, но
и спрогнозировать гипотетически ещё
более эффективные или гораздо более
критические.

21.

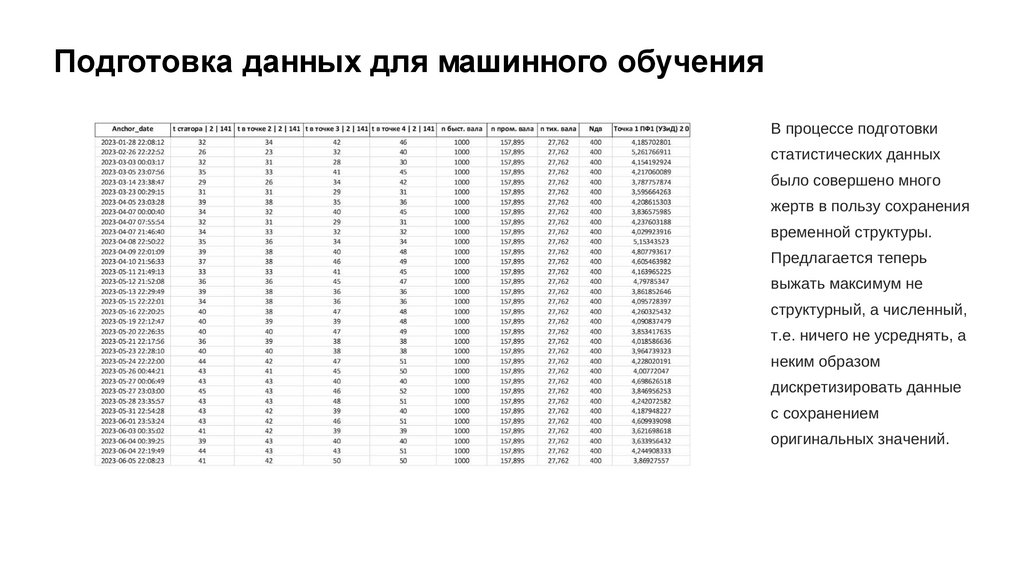
Подготовка данных для машинного обучения
В процессе подготовки
статистических данных
было совершено много
жертв в пользу сохранения
временной структуры.
Предлагается теперь
выжать максимум не
структурный, а численный,
т.е. ничего не усреднять, а
неким образом
дискретизировать данные
с сохранением
оригинальных значений.

22.

Парето оптимизация Парето оптимизации. Выбор модели
машинного обучения
Классические модели регрессии (линейная, полиномиальная, ridge, lasso, и т.д.)
Быстро учатся, легко интерпретируются. Плохо работают для сложных зависимостей
Ансамбли на основе деревьев
Моделируют сложные нелинейные зависимости, хорошо работают с категориальными переменными. Хорошо
интерпретируемы. Склонны к переобучению, требуют детальной настройки гиперпараметров
Нейронные сети
Лучшая точность, выявление самых нетривиальных зависимостей. Требуется подбор архитектуры.
Интерпретируемость на уровне "черный ящик"

23.

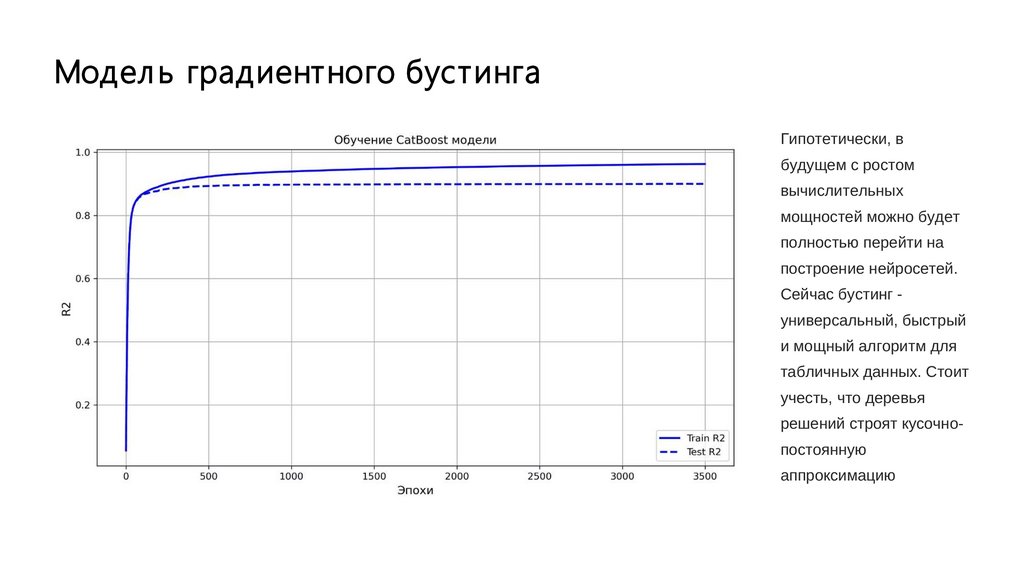
Модел ь градиентного бустинга
Гипотетически, в
будущем с ростом
вычислительных
мощностей можно будет
полностью перейти на
построение нейросетей.
Сейчас бустинг универсальный, быстрый
и мощный алгоритм для
табличных данных. Стоит
учесть, что деревья
решений строят кусочнопостоянную
аппроксимацию

24.

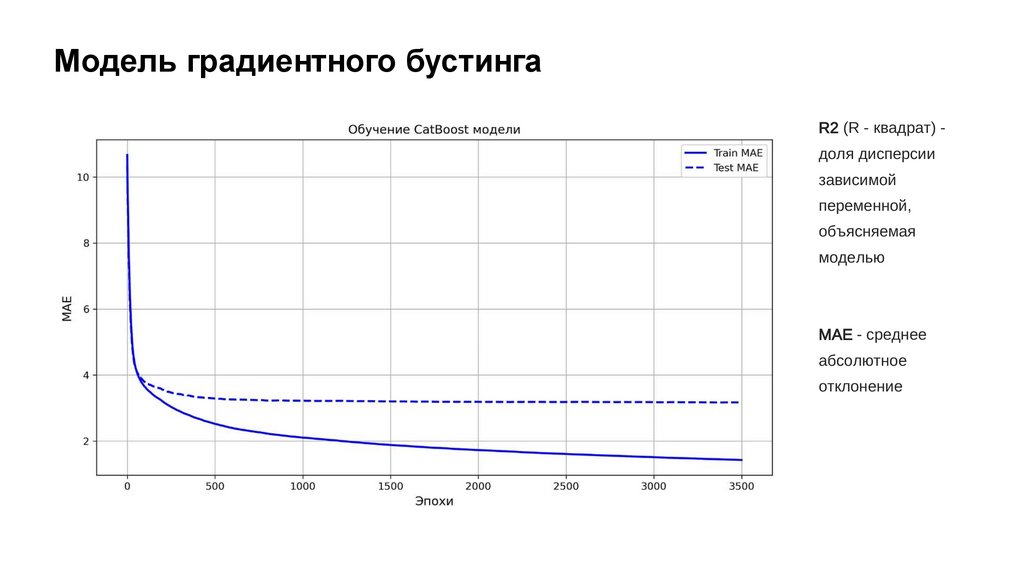
Модель градиентного бустинга
R2 (R - квадрат) доля дисперсии
зависимой
переменной,
объясняемая
моделью
MAE - среднее
абсолютное
отклонение

25.

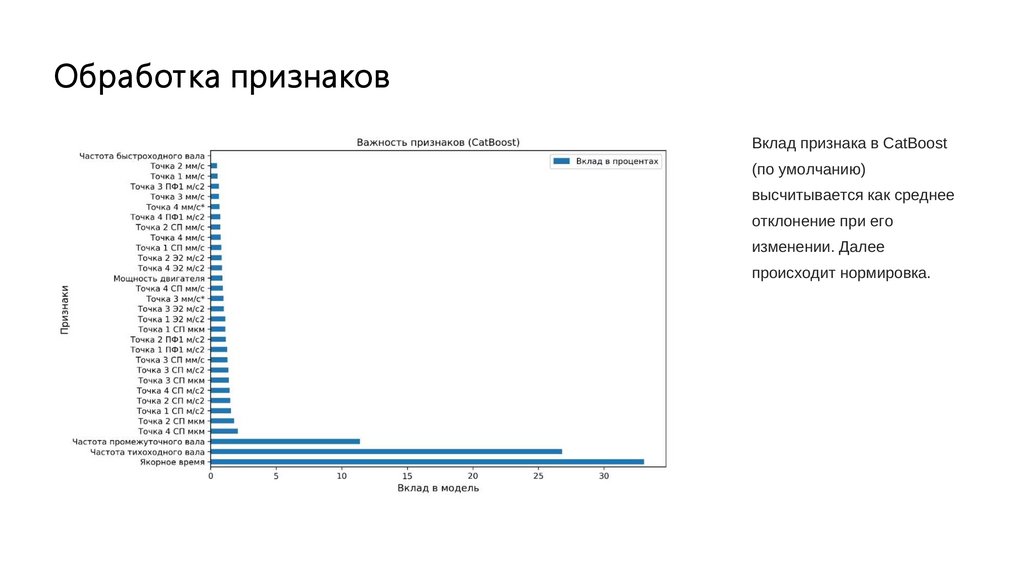
Обработка признаков
Вклад признака в CatBoost
(по умолчанию)
высчитывается как среднее
отклонение при его
изменении. Далее
происходит нормировка.

26.

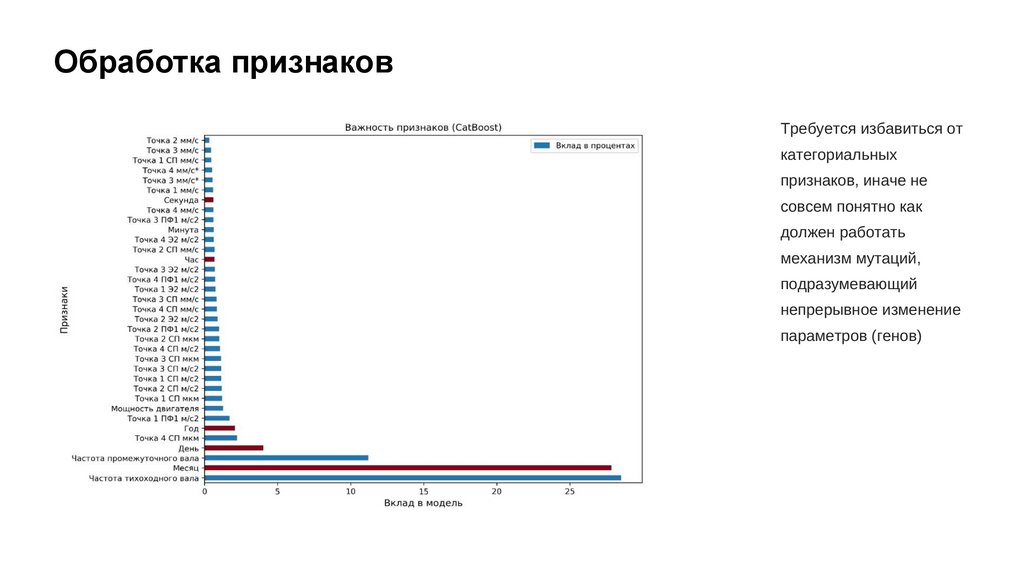
Обработка признаков
Требуется избавиться от
категориальных
признаков, иначе не
совсем понятно как
должен работать
механизм мутаций,
подразумевающий
непрерывное изменение
параметров (генов)

27.

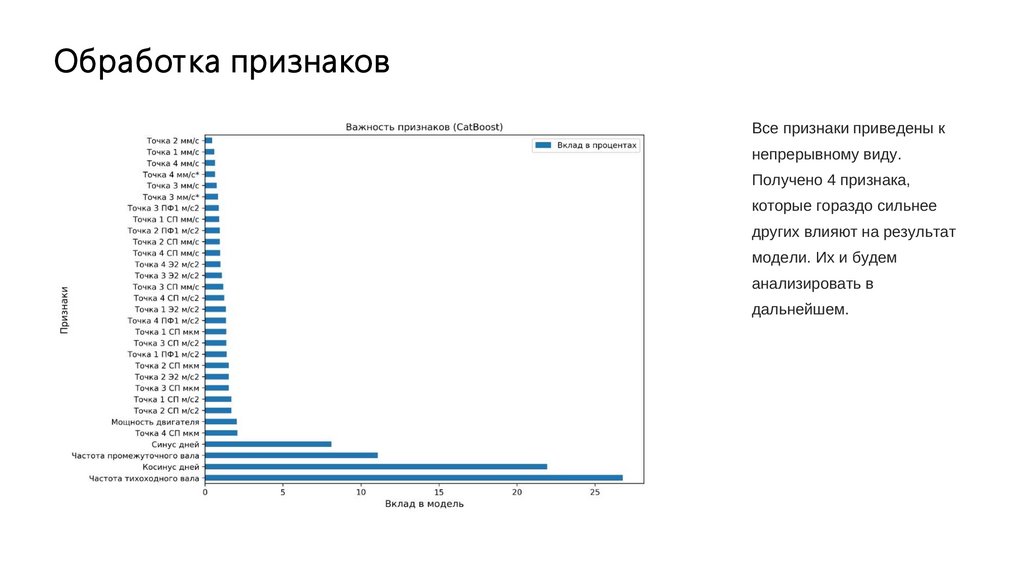
Обработка признаков
Все признаки приведены к
непрерывному виду.
Получено 4 признака,
которые гораздо сильнее
других влияют на результат
модели. Их и будем
анализировать в
дальнейшем.

28.

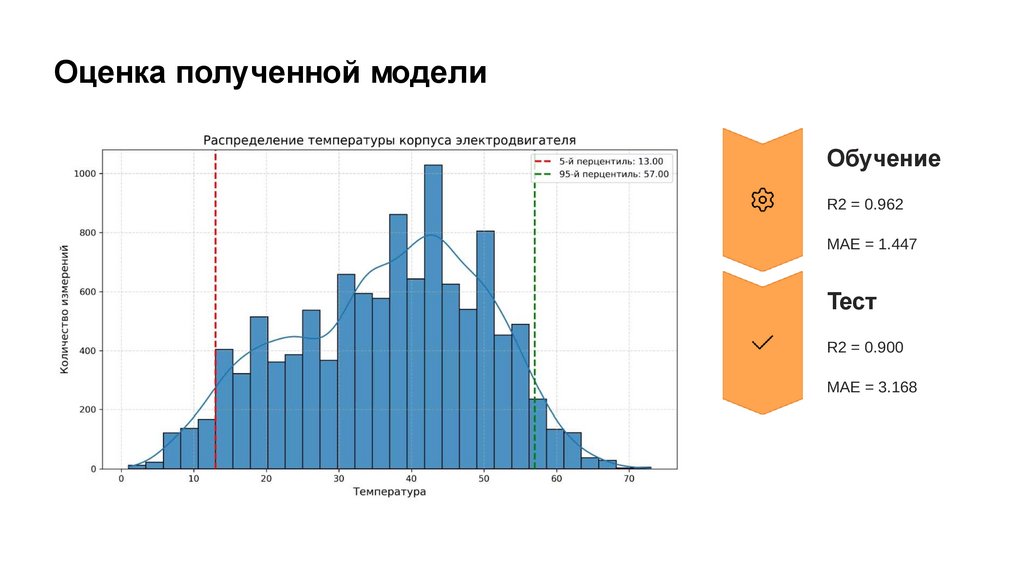
Оценка полученной модели
Обучение
R2 = 0.962
MAE = 1.447
Тест
R2 = 0.900
MAE = 3.168

29.

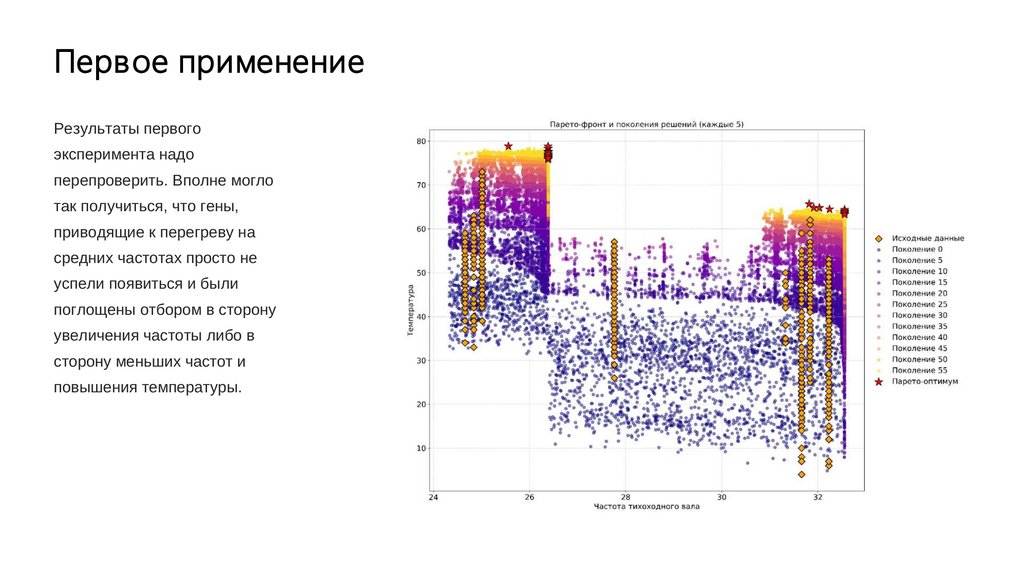
Первое применение
Результаты первого
эксперимента надо
перепроверить. Вполне могло
так получиться, что гены,
приводящие к перегреву на
средних частотах просто не
успели появиться и были
поглощены отбором в сторону
увеличения частоты либо в
сторону меньших частот и
повышения температуры.

30.

Ограничение параметров для уточнения результатов

31.

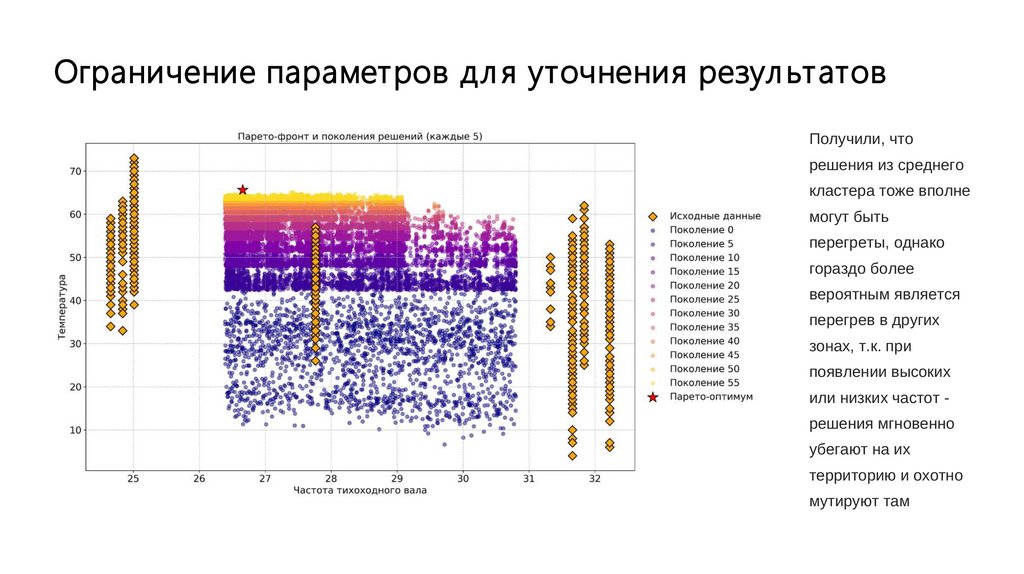
Ограничение параметров дл я уточнения резул ьтатов
Получили, что
решения из среднего
кластера тоже вполне
могут быть
перегреты, однако
гораздо более
вероятным является
перегрев в других
зонах, т.к. при
появлении высоких
или низких частот -
решения мгновенно
убегают на их
территорию и охотно
мутируют там

32.

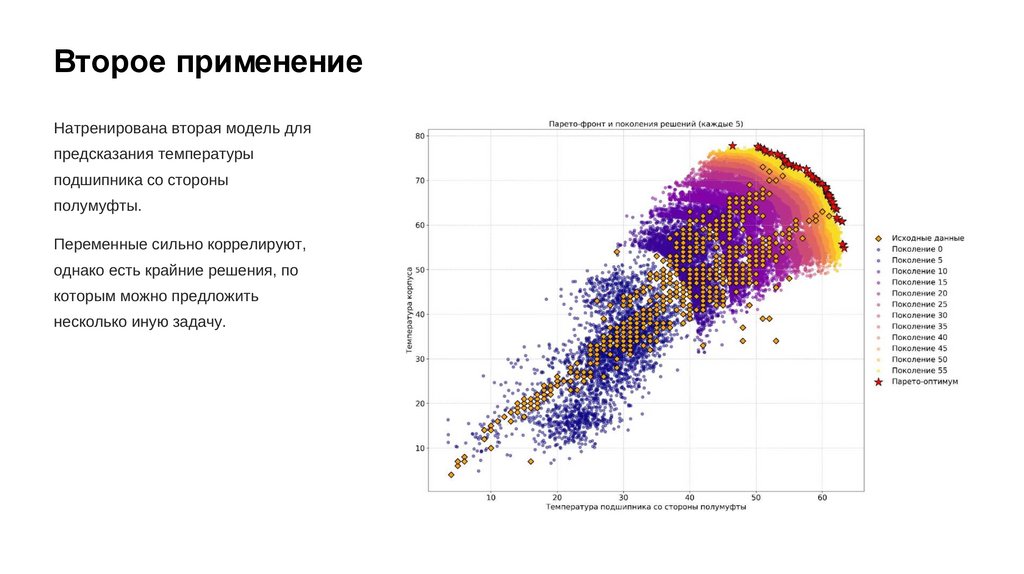
Второе применение
Натренирована вторая модель для
предсказания температуры
подшипника со стороны
полумуфты.
Переменные сильно коррелируют,
однако есть крайние решения, по
которым можно предложить
несколько иную задачу.

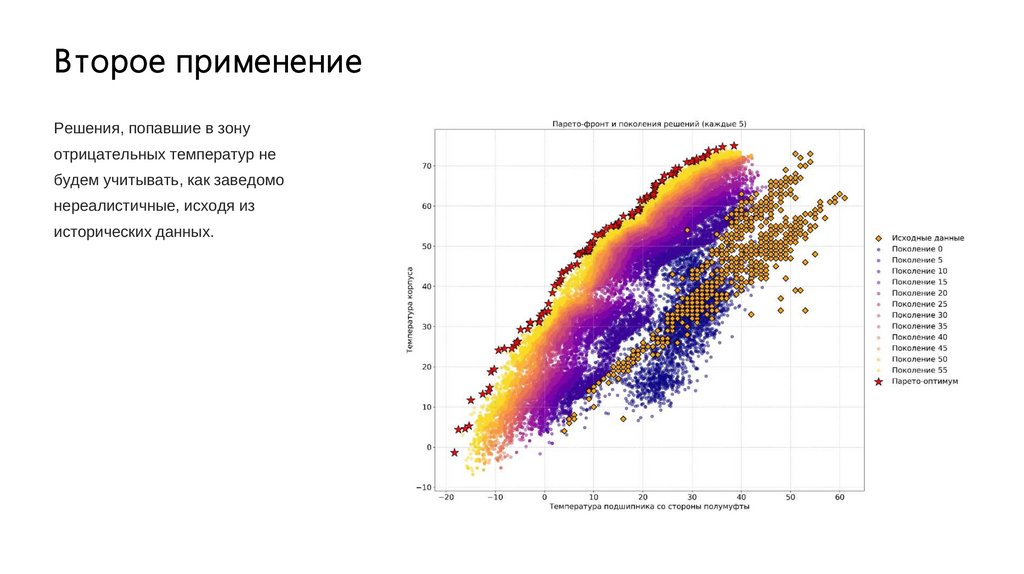
33.

В торое применение
Решения, попавшие в зону
отрицательных температур не
будем учитывать, как заведомо
нереалистичные, исходя из
исторических данных.

34.

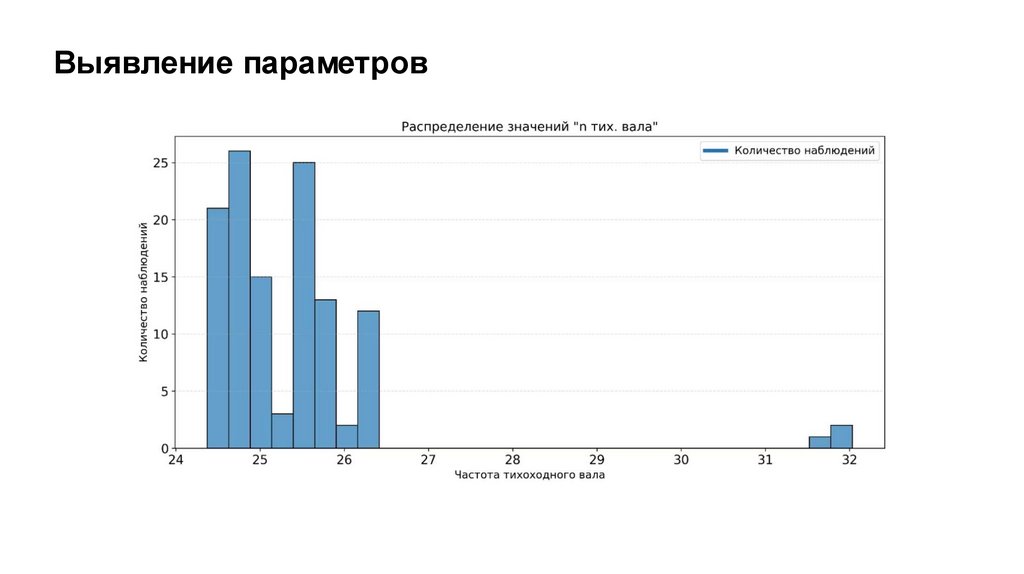
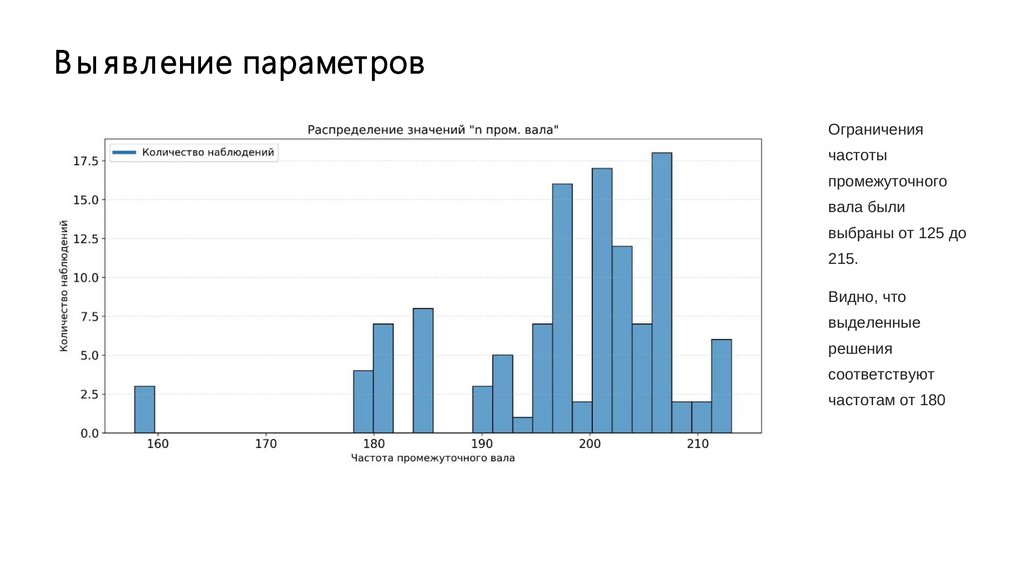
Выявление параметров

35.

В ы явление параметров
Ограничения
частоты
промежуточного
вала были
выбраны от 125 до
215.
Видно, что
выделенные
решения
соответствуют
частотам от 180

36.

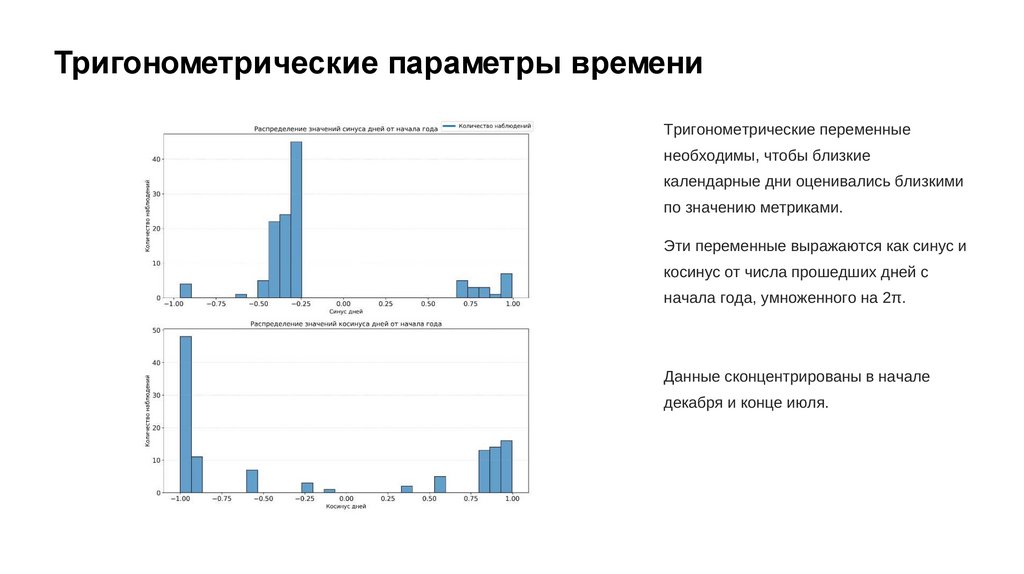
Тригонометрические параметры времени
Тригонометрические переменные
необходимы, чтобы близкие
календарные дни оценивались близкими
по значению метриками.
Эти переменные выражаются как синус и
косинус от числа прошедших дней с
начала года, умноженного на 2π.
Данные сконцентрированы в начале
декабря и конце июля.

37.

Итоги
Предобработка
Рассмотрены разные подходы к обработке данных, реализован комплекс программ для подготовки данных к разным
алгоритмам
Парето анал из
Применены методы статического выявления оптимальных решений, сделаны выводы, рассмотрен переход к
динамическому анализу и выявлены критические и оптимальные параметры
Пространство дл я улучшения
Предложены оптимальные способы дальнейшего улучшения анализа для непосредственного применения на
практике.
Дал ь нейшее применение
Реализованный программный модуль будет использован для повышения эффективности реального
производства

38.

Фрагменты эпической поэмы об оптимизационной войне
Муза, скажи мне о том многоопытном муже, который
Бустингом мощно владел и святой датасет подготовил,
Много испробовал разных обычаев медных и в генах
Грозно сбирал только те, что конвейер нагреют несчастный!
Метрики скорбь насылали, над нами ходящие боги:
Признаки слабые были великим позором для стана
Ахейцев. Плакали жёны много эпох безутешно.
Ныне же Гарпии взяли бесславных и быстроходных:
Валов отбросили часть и время разбили когтями.
Уничтожение неоптимального конвейера
Все уж другие, погибели верной избегшие,были
Сладким нектаром для многих деревьев решений глубоких.

39.

Ф рагменты эпической поэмы об оптимизационной войне
Встала из мрака младая и средняя по абсолютным
Числам ошибка модели и стала готова для генов
Почва. Конвейеров часть зловещий туман ощутила:
«О необузданный, снова замыслил найти оптимальных;
Снова о бое мечтает и рад он с богами сразиться.»
Что за наглец неотступный! Прикладных математик потомок!
Скрещивал мощности он, виброскоростью правил всевластно.
Всё на земле изменяется, всё скоротечно; когда же
Температур достигали подшипники, корпус нагрелся
Гнев народа из-за поломки в результате аномалий
Безумный! Скажи поскорее, Зевесова дщерь, кто избегнул
Смерти бесславной от рук кибернетики дивного сына.