Аппроксимация и интерполяция. Тема II

1. Методы приближенных вычислений

Лекция 3

2.

Тема II. Аппроксимация и интерполяция
§ 1. Общие понятия
Аппроксимацией называется замена одних
математических объектов другими математическими
объектами, близкими к первым в некотором смысле.
Замена функции f(x) другой функцией g(x) ,
«близкой» к f(x).

3.

Пример 1. Задача о минимальном квадратичном
отклонении.
Постановка задачи
Дано: x0, x1, ..., xn — значения аргумента (узлы),
f(x0), f(x1), ..., f(xn) — значения f(x) в узлах.
Найти функцию g(x) вида:
(среди всех функций этого вида).

4.

Пример 2. Задача об интерполяционном многочлене.
Постановка задачи
Дано: x0, x1, ..., xn — узлы,
f(x0), f(x1), ..., f(xn) — значения f(x) в узлах.
Найти функцию g(x) (многочлен степени m) такую,
что g(xi) = f(xi), i=0,...,n.
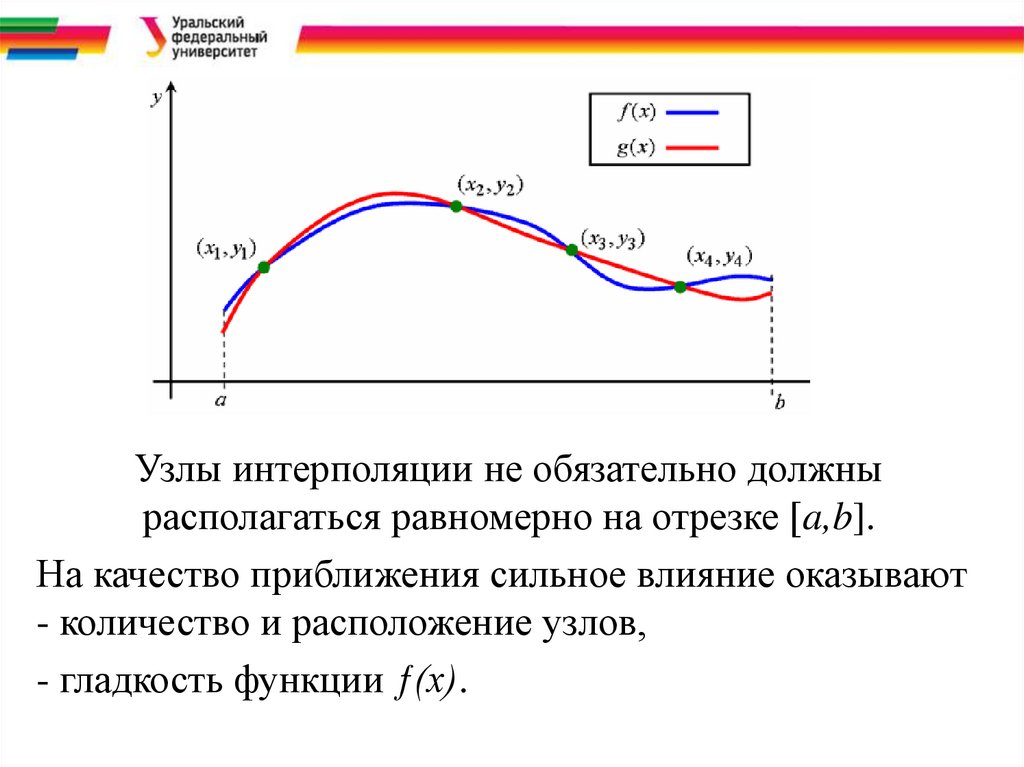
Геометрически – интерполирование представляет
собой построение кривой, проходящей через заданное
количество точек.

5.

Узлы интерполяции не обязательно должны
располагаться равномерно на отрезке [a,b].
На качество приближения сильное влияние оказывают
- количество и расположение узлов,
- гладкость функции ƒ(x).

6.

Если в дальнейшем нужно вычислить значение g(x)
для
, то говорят об интерполяции функции.
Если
(т.е. лежит за пределами отрезка,
содержащего узлы), то говорят об экстраполяции.
Решением задачи интерполирования является
использование многочлена Тейлора степени m:

7.

Погрешность метода — остаточный член формулы
Тейлора в форме Лагранжа:
где с лежит между х и х0.
При этом, если не принадлежит интервалу сходимости
ряда Тейлора, то погрешность не уменьшается с ростом
m.

8.

§ 2. Существование и единственность
интерполяционного многочлена
Постановка задачи.
Дано: x0, x1, ..., xn — узлы, (x0<x1<…<xn)
f0, f1, ..., fn — значения f(x) в узлах.
Найти:
n
Ln x ak k x , k x x k
k 0
такой, что L(xi) = fi, i=0,...,n.

9.

Теорема. Существует единственный многочлен
степени m = n, удовлетворяющий условиям задачи об
интерполяционном многочлене.
Доказательство.
Чтобы найти многочлен Ln(x) нужно найти
коэффициенты a0,a1,...an, которые удовлетворяют СЛУ
L i 0, i 0, n

10.

В системе (n+1) неизвестная и
Главный определитель системы
(n+1) уравнение.
- определитель Вандермонда.

11.

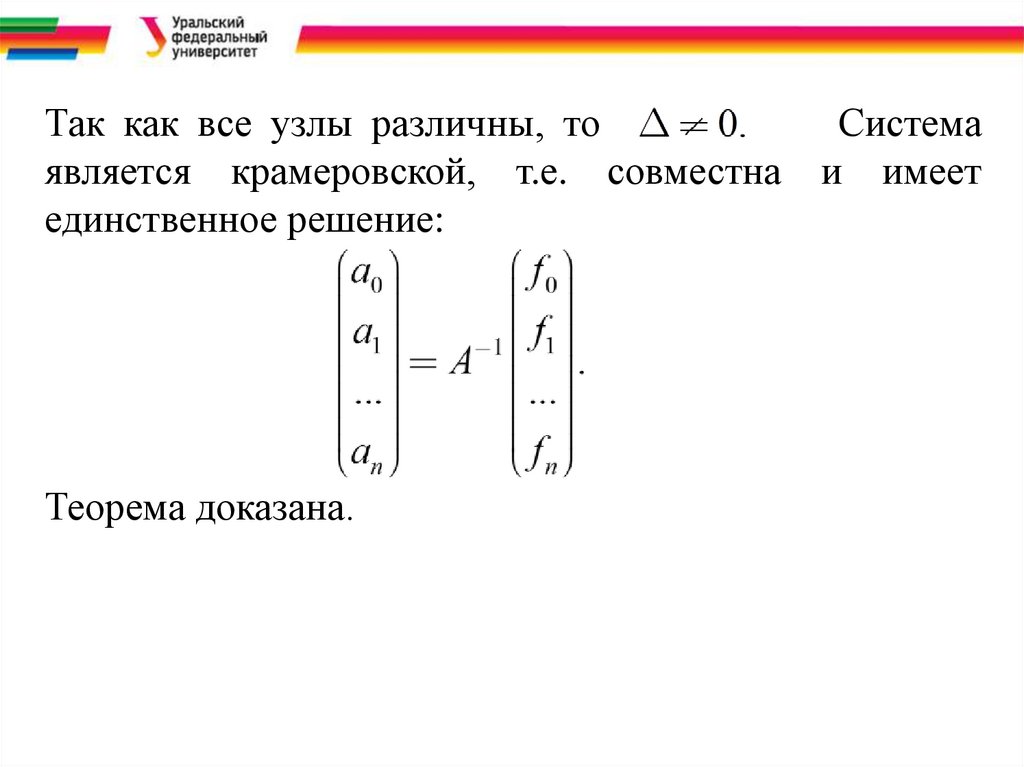
Так как все узлы различны, то
Система
является крамеровской, т.е. совместна и имеет
единственное решение:
Теорема доказана.

12.

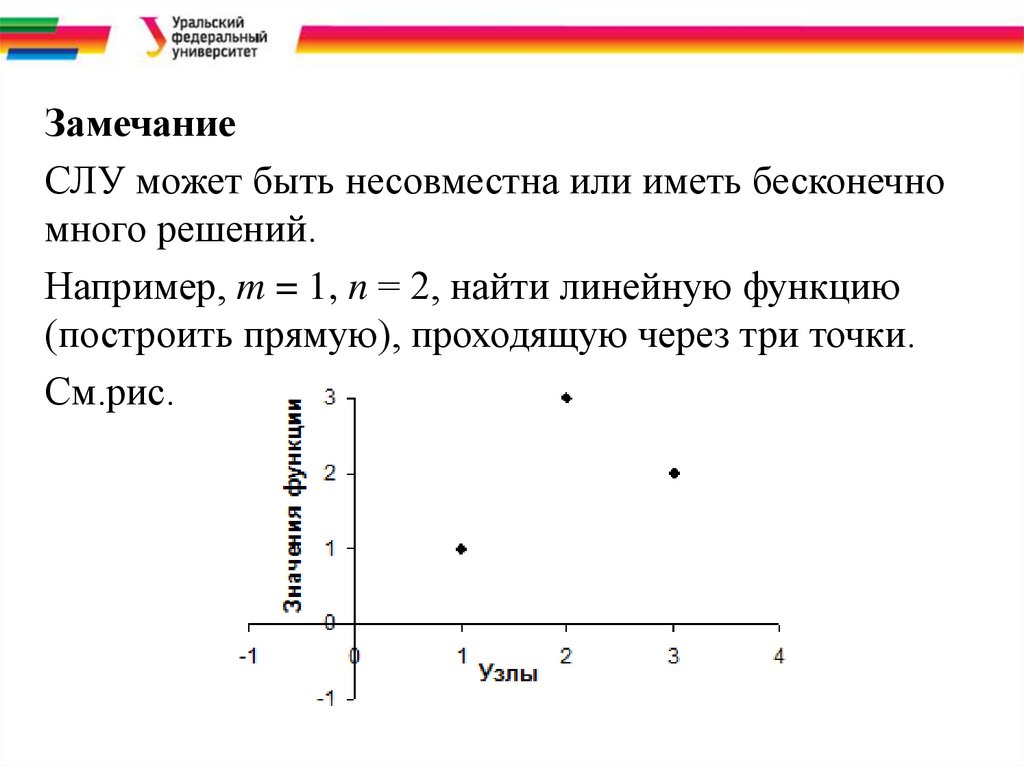
Замечание
СЛУ может быть несовместна или иметь бесконечно
много решений.
Например, m = 1, n = 2, найти линейную функцию
(построить прямую), проходящую через три точки.
См.рис.

13.

Если m > n, СЛУ имеет бесконечно много решений.
Например, m = 2, n = 1, найти квадратичную функцию
(построить параболу), проходящую через две точки.
См.рис.

14.

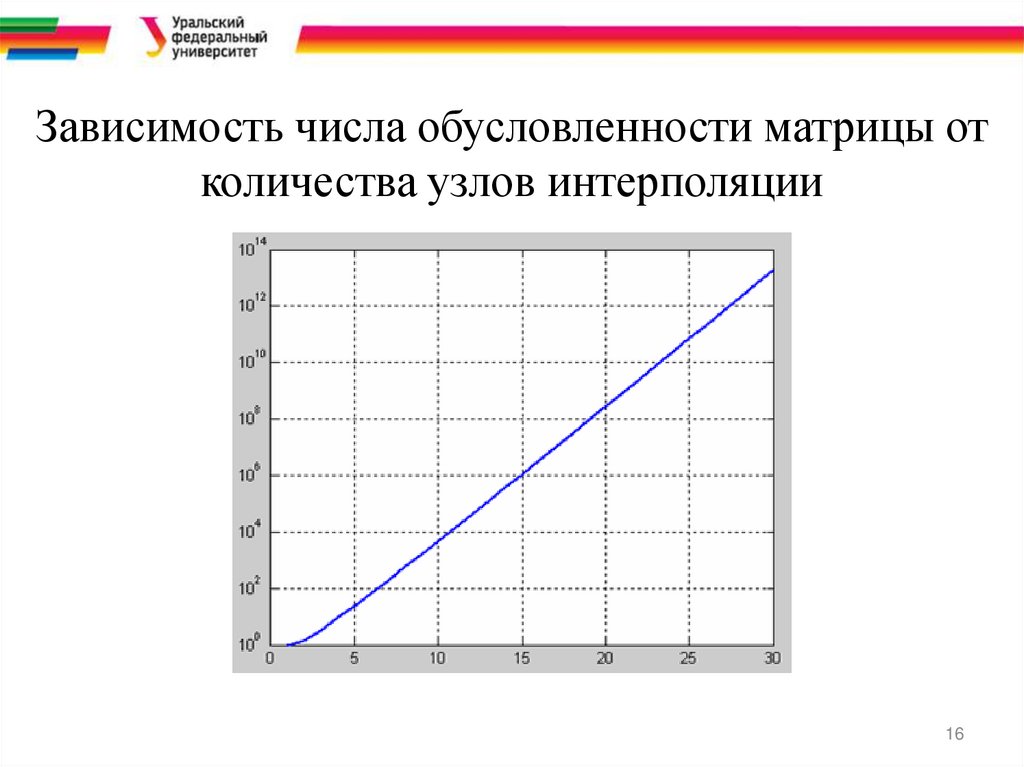
Число обусловленности матрицы этой системы быстро
растет с ростом числа узлов интерполяции, что может
привести к большим ошибкам при решении системы с
ней.
14

15.

Число обусловленности
Число обусловленности функции по отношению к
аргументу измеряет, насколько может измениться
выходное значение функции при небольшом изменении
входного аргумента.
Это используется, чтобы измерить, насколько
чувствительна функция к изменениям или ошибкам на
входе, и на сколько ошибка на выходе является
результатом ошибки на входе.
f
f
f
f max
max
, где x малое
X x
X
x x
15

16.

Зависимость числа обусловленности матрицы от
количества узлов интерполяции
16