Расчет потоков с использованием матриц. Неритмичные потоки

1.

Расчет потоков с использованием матриц. Неритмичные потоки
НИУ МГСУ 2025

2.

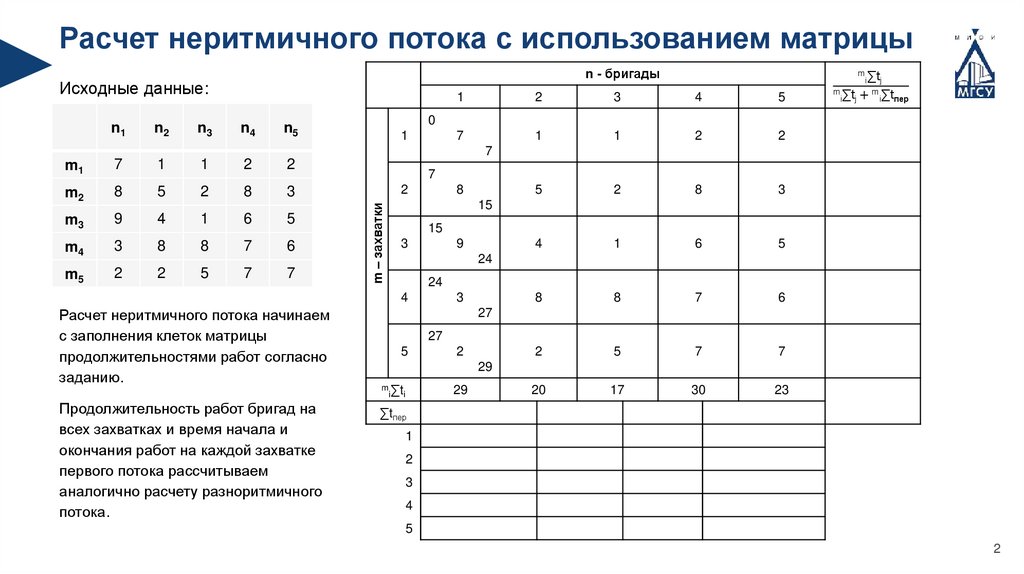
Расчет неритмичного потока с использованием матрицы
n - бригады
Исходные данные:
n1
n2
n3
1
n4
2
3
4
5
1
1
2
2
5
2
8
3
4
1
6
5
8
8
7
6
2
5
7
7
20
17
30
23
m ∑t
i j
m ∑t + m ∑t
i j
i пер
0
n5
1
7
7
7
1
1
2
2
m2
8
5
2
8
3
m3
9
4
1
6
5
m4
3
8
8
7
6
m5
2
2
5
7
7
7
2
m – захватки
m1
8
15
15
3
9
24
24
4
Расчет неритмичного потока начинаем
с заполнения клеток матрицы
продолжительностями работ согласно
заданию.
Продолжительность работ бригад на
всех захватках и время начала и
окончания работ на каждой захватке
первого потока рассчитываем
аналогично расчету разноритмичного
потока.
3
27
27
5
2
29
m ∑t
i i
29
∑tпер
1
2
3
4
5
2

3.

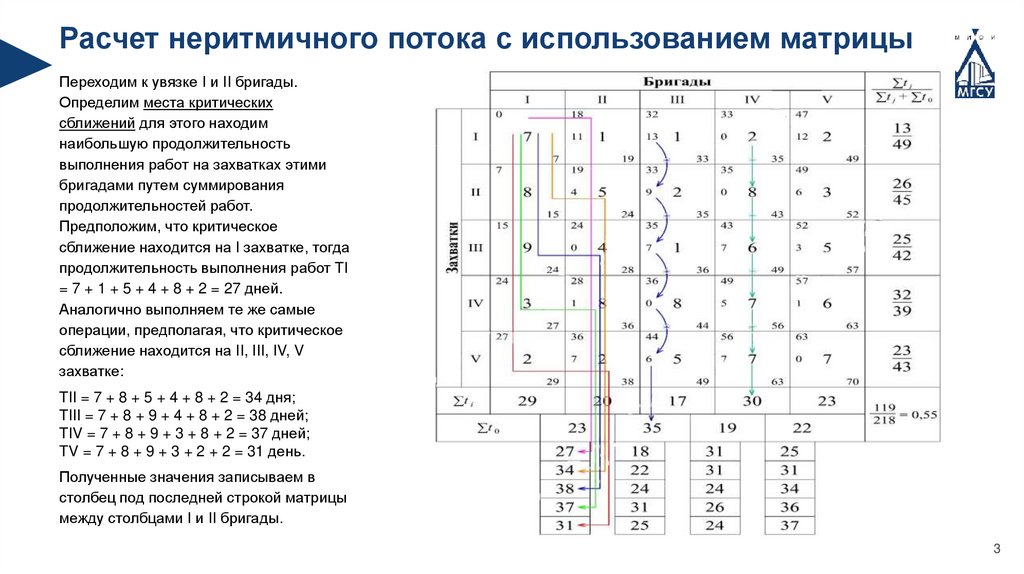
Расчет неритмичного потока с использованием матрицы
Переходим к увязке I и II бригады.
Определим места критических
сближений для этого находим
наибольшую продолжительность
выполнения работ на захватках этими
бригадами путем суммирования
продолжительностей работ.
Предположим, что критическое
сближение находится на I захватке, тогда
продолжительность выполнения работ TI
= 7 + 1 + 5 + 4 + 8 + 2 = 27 дней.
Аналогично выполняем те же самые
операции, предполагая, что критическое
сближение находится на II, III, IV, V
захватке:
TII = 7 + 8 + 5 + 4 + 8 + 2 = 34 дня;
TIII = 7 + 8 + 9 + 4 + 8 + 2 = 38 дней;
TIV = 7 + 8 + 9 + 3 + 8 + 2 = 37 дней;
TV = 7 + 8 + 9 + 3 + 2 + 2 = 31 день.
Полученные значения записываем в
столбец под последней строкой матрицы
между столбцами I и II бригады.
3

4.

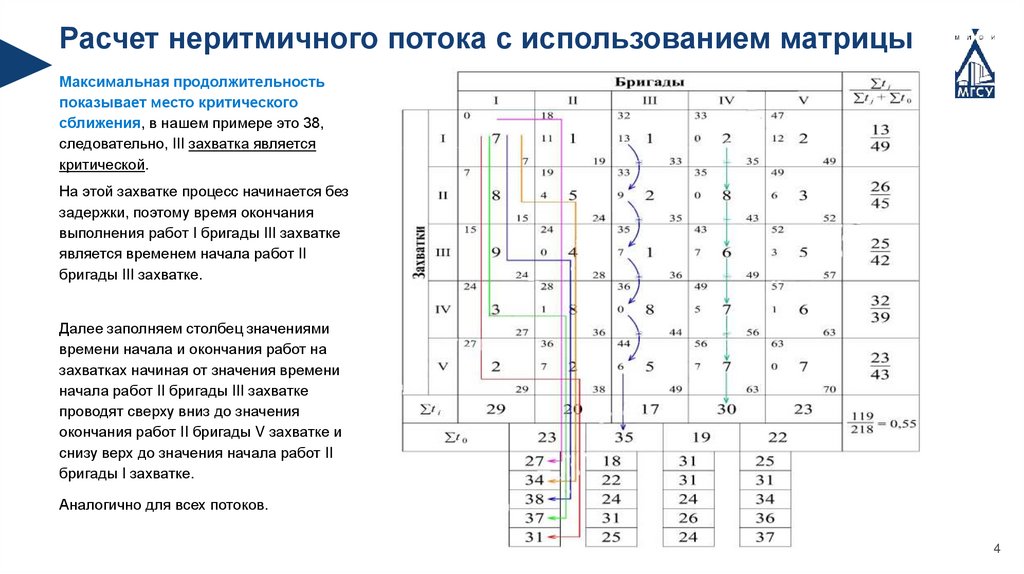
Расчет неритмичного потока с использованием матрицы
Максимальная продолжительность
показывает место критического
сближения, в нашем примере это 38,
следовательно, III захватка является
критической.
На этой захватке процесс начинается без
задержки, поэтому время окончания
выполнения работ I бригады III захватке
является временем начала работ II
бригады III захватке.
Далее заполняем столбец значениями
времени начала и окончания работ на
захватках начиная от значения времени
начала работ II бригады III захватке
проводят сверху вниз до значения
окончания работ II бригады V захватке и
снизу верх до значения начала работ II
бригады I захватке.
Аналогично для всех потоков.
4

5.

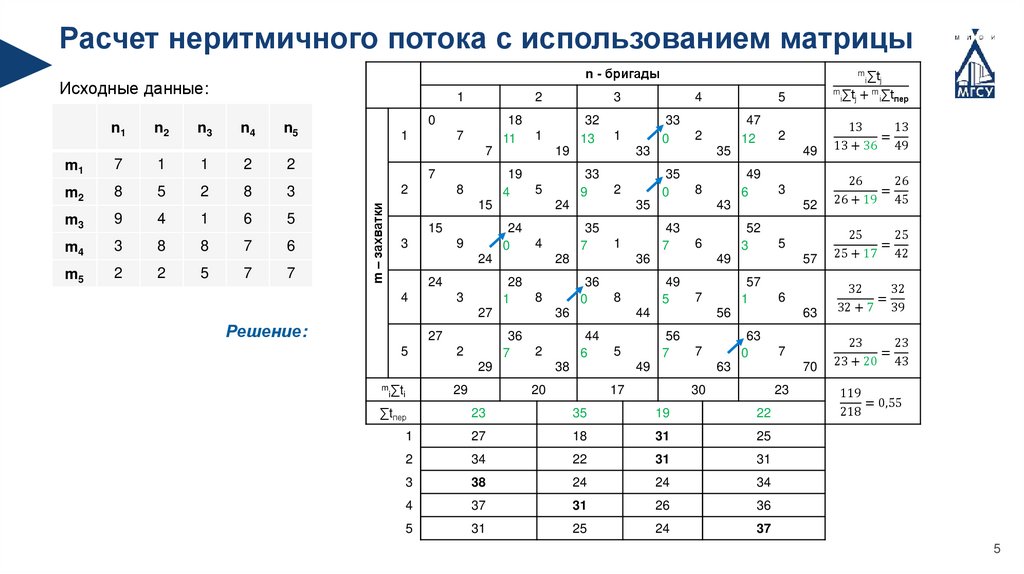
Расчет неритмичного потока с использованием матрицы
n - бригады
Исходные данные:
n1
n2
n3
n4
n5
7
1
1
2
2
1
2
7
18
11 1
0
1
7
m2
8
5
2
8
3
m3
9
4
1
6
5
m4
3
8
8
7
6
m5
2
2
5
7
7
7
2
m – захватки
m1
15
9
24
28
28
8
1
3
27
Решение:
27
5
36
36
2
7
2
29
m ∑t
i i
29
44
44
6
38
7
49
20
63
0
30
23
35
19
22
1
27
18
31
25
2
34
22
31
31
3
38
24
24
34
4
37
31
26
36
5
31
25
24
37
70
23
23
=
23 + 20 43
7
23
∑tпер
63
32
32
=
32 + 7 39
6
63
17
57
25
25
=
25 + 17 42
5
56
56
7
5
57
1
7
52
26
26
=
26 + 19 45
3
49
49
5
8
52
3
6
36
36
0
49
6
8
49
13
13
=
13 + 36 49
2
43
43
7
1
47
12
2
35
35
7
5
35
35
0
2
24
24
33
0
33
33
9
24
4
0
4
1
19
15
4
32
13
19
5
4
8
3
3
m ∑t
i j
m ∑t + m ∑t
i j
i пер
119
= 0,55
218
5

6.

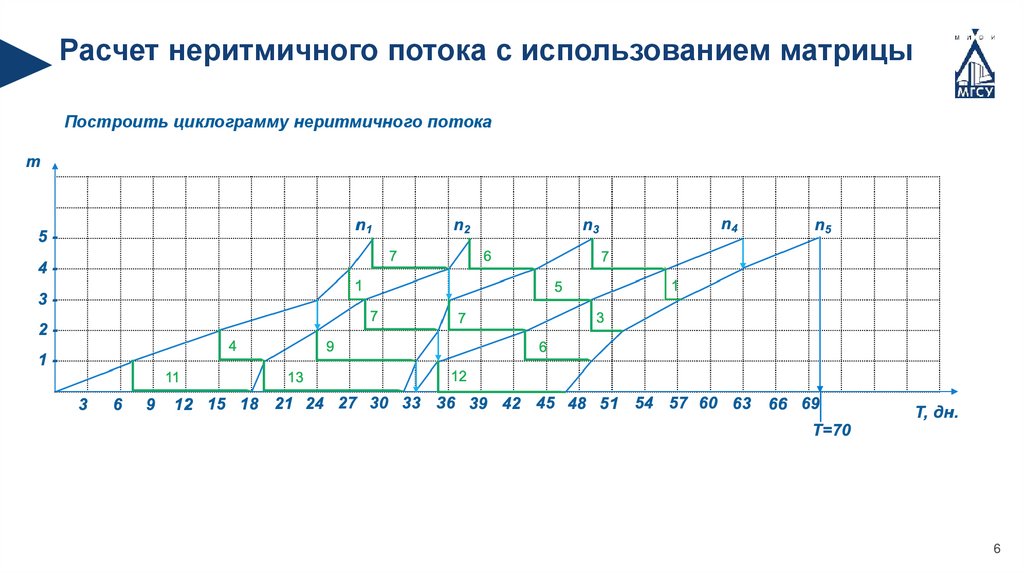
Расчет неритмичного потока с использованием матрицы
Построить циклограмму неритмичного потока
m
n1
5-
n2
6
7
4-
4
111
3
6
9
3
7
9
13
1
5
7
2-
n5
7
1
3-
n4
n3
6
12
12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63
66 69
T, дн.
T=70
6

7.

Расчет неритмичного потока с использованием матрицы
Сокращение продолжительности строительства комплекса за счет совмещения процессов
Рассчитать продолжительность строительства комплекса из 4 объектов со следующими неритмичными
потоками:
1 – работы нулевого цикла;
2 – возведение надземной части;
3 – санитарно-технические работы;
4 – электромонтажные работы;
5 – отделочные работы.
Проверить, как изменится продолжительность строительства, если работы 3 и 4 потоков выполняются
параллельно и независимо друг от друга, а 5 поток начинает работу после завершения 3 и 4.
Продолжительность потоков задана в условных единицах времени.
Построить циклограмму по окончательному варианту.
Для решения подобных задач необходимо рассчитать две матрицы:
первую – при заданных условиях, но без совмещения процессов;
а вторую – при совмещении указанных процессов. Затем результаты расчета следует сравнить.
7

8.

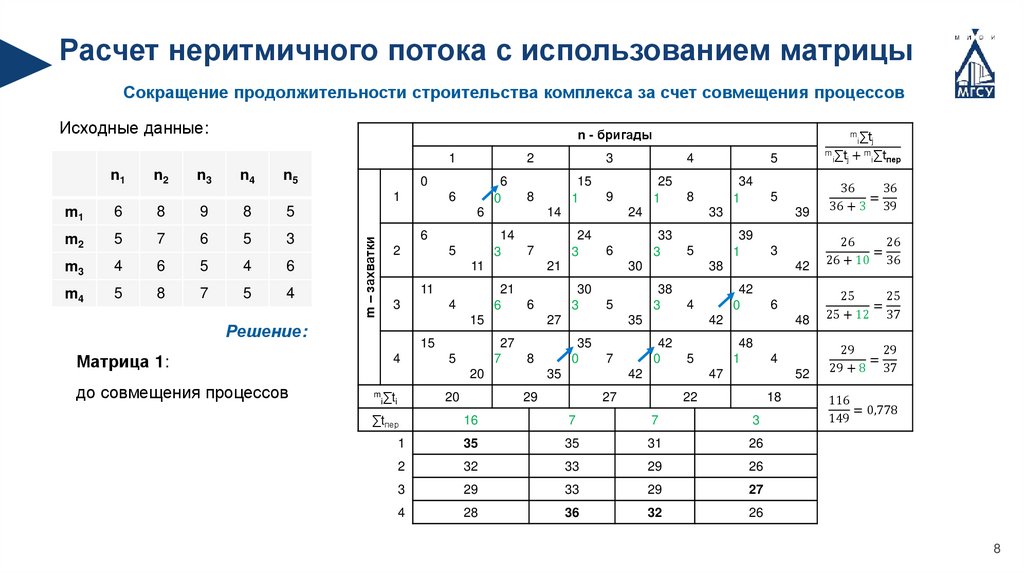
Расчет неритмичного потока с использованием матрицы
Сокращение продолжительности строительства комплекса за счет совмещения процессов
Исходные данные:
n - бригады
1
n1
n2
n3
n4
n5
0
1
6
8
9
8
5
m2
5
7
6
5
3
m3
4
6
5
4
6
m4
5
8
7
5
4
до совмещения процессов
6
6
2
11
4
15
27
5
20
m ∑t
i i
20
35
5
42
29
48
1
22
16
7
7
3
1
35
35
31
26
2
32
33
29
26
3
29
33
29
27
4
28
36
32
26
52
29
29
=
29 + 8 37
4
18
∑tпер
48
25
25
=
25 + 12 37
6
47
27
42
26
26
=
26 + 10 36
3
42
42
0
7
42
0
4
35
35
0
39
1
5
39
36
36
=
36 + 3 39
5
38
38
3
5
34
1
8
30
30
3
5
33
33
3
6
21
27
8
7
25
1
24
24
3
21
6
6
4
9
14
15
4
15
1
14
7
3
5
3
3
8
11
Решение:
Матрица 1:
6
0
6
m – захватки
m1
2
m ∑t
i j
m ∑t + m ∑t
i j
i пер
116
= 0,778
149
8

9.

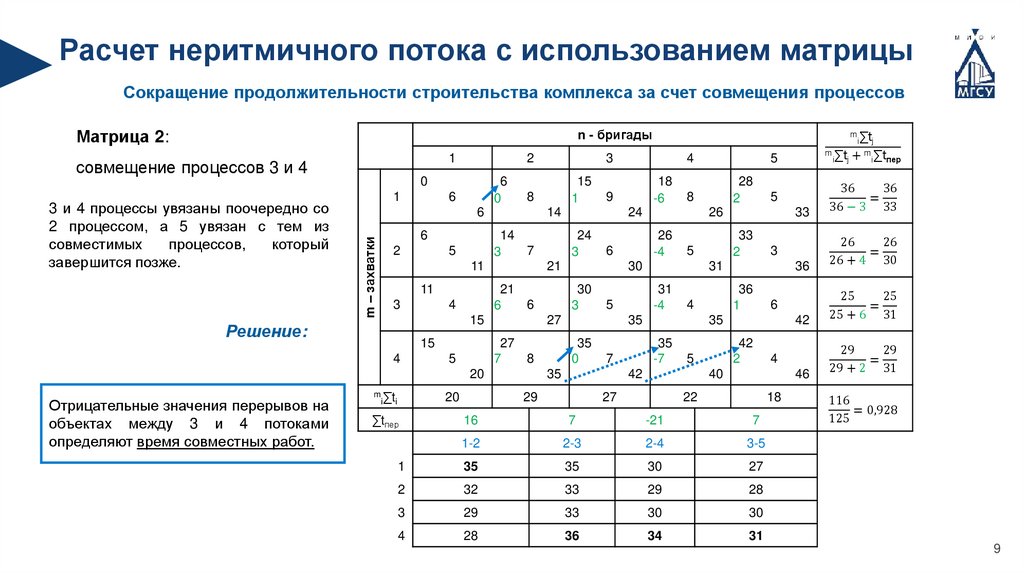
Расчет неритмичного потока с использованием матрицы
Сокращение продолжительности строительства комплекса за счет совмещения процессов
Матрица 2:
n - бригады
1
совмещение процессов 3 и 4
0
1
6
0
6
6
2
11
4
15
4
27
27
8
7
5
20
Отрицательные значения перерывов на
объектах между 3 и 4 потоками
определяют время совместных работ.
m ∑t
i i
20
∑tпер
35
5
42
29
42
2
22
7
-21
7
1-2
2-3
2-4
3-5
1
35
35
30
27
2
32
33
29
28
3
29
33
30
30
4
28
36
34
31
46
29
29
=
29 + 2 31
4
18
16
42
25
25
=
25 + 6 31
6
40
27
36
26
26
=
26 + 4 30
3
35
35
-7
7
36
1
4
35
35
0
33
2
5
33
36
36
=
36 − 3 33
5
31
31
-4
5
28
2
8
30
30
3
5
26
26
-4
6
21
15
18
-6
24
24
3
21
6
6
4
9
14
11
Решение:
15
1
14
7
3
5
3
3
8
6
m – захватки
3 и 4 процессы увязаны поочередно со
2 процессом, а 5 увязан с тем из
совместимых
процессов,
который
завершится позже.
2
m ∑t
i j
m ∑t + m ∑t
i j
i пер
116
= 0,928
125
9

10.

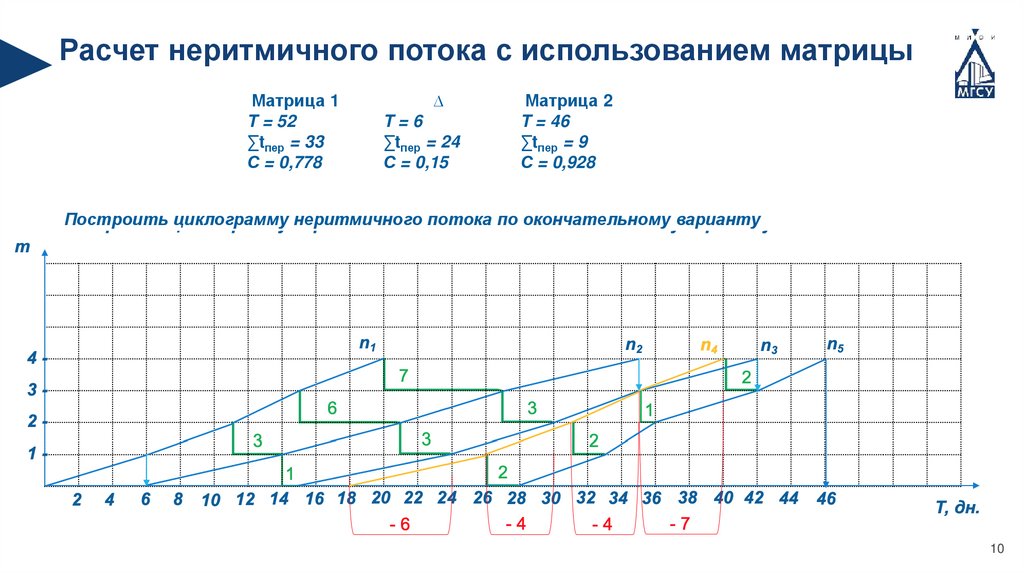
Расчет неритмичного потока с использованием матрицы
Матрица 1
T = 52
∑tпер = 33
С = 0,778
∆
T=6
∑tпер = 24
С = 0,15
Матрица 2
T = 46
∑tпер = 9
С = 0,928
Построить циклограмму неритмичного потока по окончательному варианту
m
n1
4-
n2
n4
7
33
12
4
6
8
n5
2
6
2-
n3
3
3
1
2
2
1
10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44
-4
-7
-6
-4
46
T, дн.
10

11.

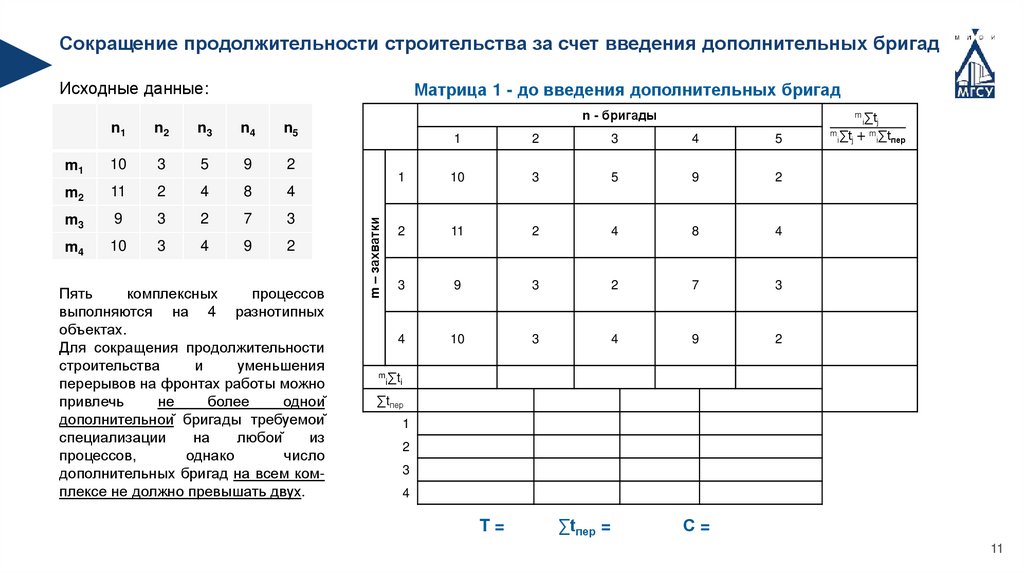
Сокращение продолжительности строительства за счет введения дополнительных бригад
Исходные данные:
Матрица 1 - до введения дополнительных бригад
n2
n3
n4
n5
m1
10
3
5
9
2
m2
11
2
4
8
4
m3
9
3
2
7
3
m4
10
3
4
9
2
Пять
комплексных
процессов
выполняются на 4 разнотипных
объектах.
Для сокращения продолжительности
строительства
и
уменьшения
перерывов на фронтах работы можно
привлечь
не
более
одной
дополнительной бригады требуемой
специализации
на
любой
из
процессов,
однако
число
дополнительных бригад на всем комплексе не должно превышать двух.
m – захватки
n1
n - бригады
1
2
3
4
5
1
10
3
5
9
2
2
11
2
4
8
4
3
9
3
2
7
3
4
10
3
4
9
2
m ∑t
i j
m ∑t + m ∑t
i j
i пер
m ∑t
i i
∑tпер
1
2
3
4
T=
∑tпер =
С=
11

12.

Матрица 1 дала следующие результаты: Тстр= 75, Σtпер= 113, с = 0,49.
Обратим внимание, что Σtпер превысила суммарную продолжительность работы всех
бригад на всех объектах (ΣTj=110).
12

13.

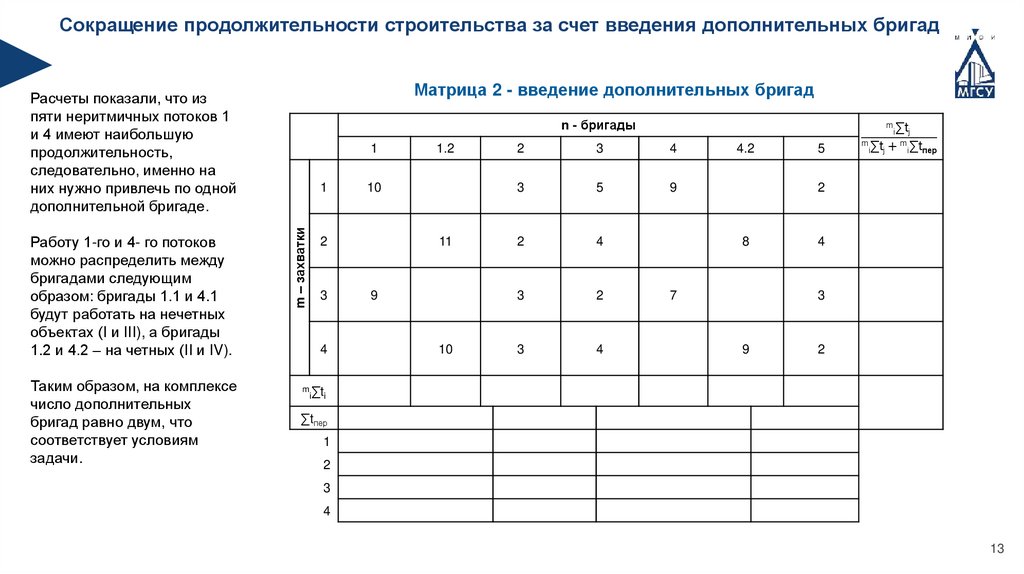
Сокращение продолжительности строительства за счет введения дополнительных бригад
Матрица 2 - введение дополнительных бригад
Расчеты показали, что из
пяти неритмичных потоков 1
и 4 имеют наибольшую
продолжительность,
следовательно, именно на
них нужно привлечь по одной
дополнительной бригаде.
Таким образом, на комплексе
число дополнительных
бригад равно двум, что
соответствует условиям
задачи.
1
1
m – захватки
Работу 1-го и 4- го потоков
можно распределить между
бригадами следующим
образом: бригады 1.1 и 4.1
будут работать на нечетных
объектах (I и III), а бригады
1.2 и 4.2 – на четных (II и IV).
n - бригады
10
2
3
4
1.2
11
9
10
2
3
4
3
5
9
2
4
3
2
3
4
4.2
5
m ∑t
i j
m ∑t + m ∑t
i j
i пер
2
8
7
4
3
9
2
m ∑t
i i
∑tпер
1
2
3
4
13

14.

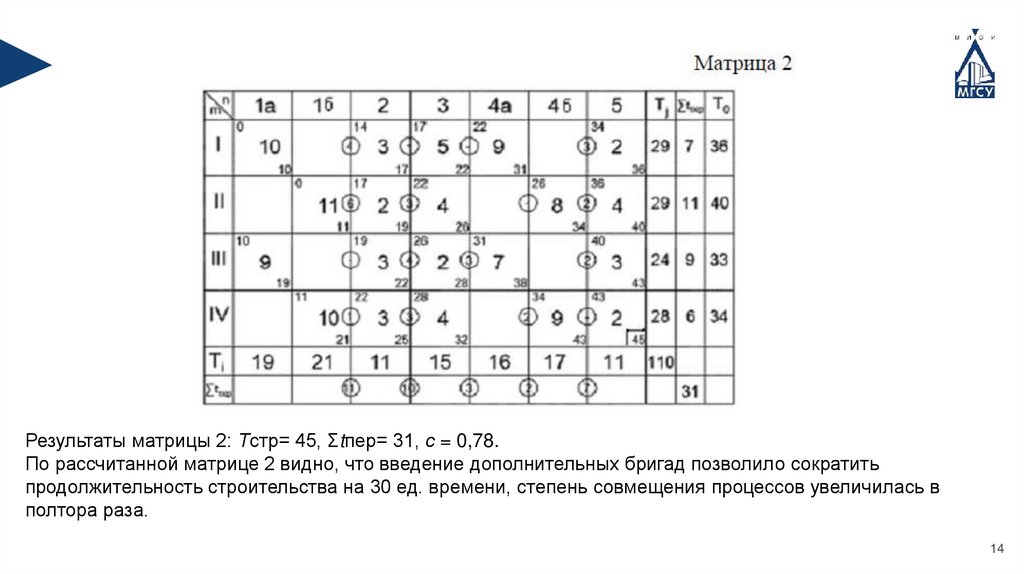
Результаты матрицы 2: Тстр= 45, Σtпер= 31, с = 0,78.
По рассчитанной матрице 2 видно, что введение дополнительных бригад позволило сократить
продолжительность строительства на 30 ед. времени, степень совмещения процессов увеличилась в
полтора раза.
14

15.

СПАСИБО ЗА ВНИМАНИЕ!
НИУ МГСУ 2025