Проверка статистических гипотез (Лекция №4)

1.

Проверка
статистических
гипотез

2.

Процедура сопоставления высказанно го предположения
( гипотезы) с выборочными данными называется проверкой
гипотез.
Задачи статистической проверки гипотез ставятся
следующим образом : относительно некоторой генеральной
совокупности высказывается та или иная гипотеза H . Из
этой генеральной совокупности извлекается выборка.
Требуется указать правило, при помощи которого можно
было бы по выборке решить вопрос о том, следует ли
отклонить гипотезу H или принять ее. Заметим, что
принимая гипотезу по статистическим данным мы не
доказываем ее, а лишь указываем на " большую" вероятность
ее осуществеления.

3.

Статистиче ской гипотезой (или просто гипотезой )
называют всякое предположение о генеральной совокупности,
проверяемо е по выборке.
Статистические гипотезы делятся на :
1) гипотезы о виде неизестного распределения,
2) гипотезы о параметрах распределения.
При решения этих задач одну из гипотез выделяют в
качестве основной (или нулевой) и обозначают H 0 , а другую,
противоположную к H 0 называют конкурирующей (или
альтернати вной), и обозначают H1.

4.

Имея две гипотезы H 0 и H1 , надо на основе выборки
x1 , x2 , , xn принять либо основную гипотезу H 0 , либо
конкурирую щую H1.
Правило, по которому принимается решение принять
или отклонить гипотезу H 0 (соответственно, принять или
отклонить H1` ), называется статистиче ским критерием
(или просто критерием ) проверки гипотезы H 0 .
Проверку гипотез осуществляют на основании
результатов выборки x1 , x2 , , xn , из которых формируют
функцию выборки Tn T ( x1 , x2 , , xn ), называемую
статистико й критерия.

5.

Основной принцип проверки гипотез состоит в
следующем. Множество возможных значений статистики
критерия Tn разбивается на два непересекающихся
подмножества : критическу ю область S , то есть область
отклонения гипотезы H 0 и область S принятия этой
гипотезы. Если фактически наблюдаемое значение
статистики критерия (то есть значение критерия
вычисленное по выборке : Tнабл T ( x1 , x2 , , xn )) попадает в
критическую область S , то основная гипотеза H 0
отклоняется и принимается H1 ; если Tнабл S , то гипотеза
H 0 принимается, а H1 отклоняется.

6.

При проверки гипотезы могут быть допущены следующие
ошибки :
ошибка первого рода состоит в том, что отвергается
нулевая гипотеза H 0 , когда на самом деле она верна;
ошибка второго рода состоит в том, что отвергается
альтернативная гипотеза H1 , когда она на самом деле верна.
Вероятност ь ошибки первого рода (обозначается )
называется уровнем значимости критерия .
Обычно полагают 0,05; 0,01; 0,005; 0,001.
Мощностью критерия называется вероятность
недопущения ошибки второго рода, обозначают (1 ), где
вероятность ошибки второго рода.

7.

Приведем примеры ошибок первого и второго рода.
В радиолокации : вероятность пропуска объекта,
вероятность ложной тревоги.
В экономике : риск поставщика забраковат ь
качественную партию, риск потребителя приема
бракованной партии товара.
В судебной системе : вероятность оправдания
виновного, вероятность осуждения невиновного.
Одновремен ное уменьшение ошибок первого и второго
рода возможно лишь при увеличении объема выборки.
Поэтому при заданном подыскивается критерий с
наибольшей мощностью.

8.

Методика проверки гипотез состоит в следующем.
1) Располагая выборкой x1 , x2 , , xn формируют нулевую
гипотезу H 0 и альтернативную H1.
2) Подбирают статистику критерия Tn T ( x1 , x2 , , xn ).
Обычно : U нормальное распределение, 2 распредление
" хи квадрат" , t распределение Стьюдента и другие.
3) По статистике критерия Tn и уровню значимости
определяют критическую область S (и S ). Границы области S
определяют из соотношений :
P(Tn t крп ) для
правосторонней
критической области S .

9.

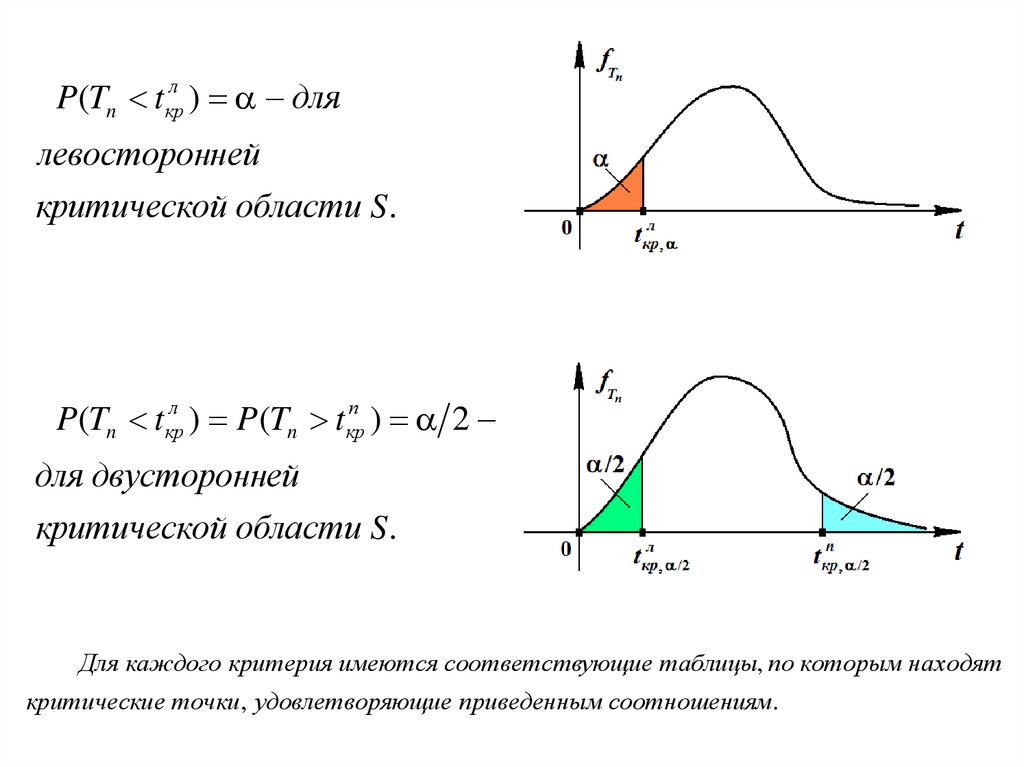
P(Tn t крл ) для
левосторонней
критической области S .
P(Tn t крл ) P(Tn t крп ) 2
для двусторонней
критической области S .
Для каждого критерия имеются соответствующие таблицы, по которым находят
критические точки, удовлетворяющие приведенным соотношениям.

10.

4) Для полученной выборки x1 , x2 , , xn вычисляют
значение критерия Tнабл T ( x1 , x2 , , xn ).
5) Если Tнабл S , то H 0 отвергают и принимают H1.
Если Tнабл S , то H 0 принимают и отвергают H1.

11.

Критерий Пирсона

12.

Пусть необходимо проверить гипотезу H 0 о том, что
случайная величина X подчиняется определенному закону
распределения, заданному функцией распределния F0 ( x),
то есть H 0 : FX ( x) F0 ( x), H1 : FX ( x) F0 ( x).
Критерием согласия называют статистический
критерий проверки гипотезы о предполагаемом законе
неизвестного распределения.
Рассмотрим критерий согласия Пирсона (или говорят
критерий χ 2 ), который основан на сравнении эмпирических
и теоретических частот, на изучении значимости их
расхождений.

13.

Разбиваем всю область значений случайной величины X
на r интервалов h1 , h2 , , hr , где hi R hi h j , i j .
r
i 1
Подсчитываем вероятности pi (i 1, r ) попадания случайной
величины X в интеравал hi , используя формулу
P(a X b) F0 (b) F0 (a ).
Тогда теоретическое число ni значений случайной
величины X , попавших в интервал hi , можно рассчитать по
формуле
ni N pi ,
где N объем выборки.
Таким образом, имеем выборку и теоретический ряд
распределения в следующем виде.

14.

1. X дискретная случайная величина
эксп.
X
n
x1
n1
x2 xr
n2 nr
теор.
X x1 x2 xr
n n1 n2 nr
2. X непрерывная случайная величина
эксп.
h h1
n n1
h2 hr
n2 nr
теор.
h h1 h2 hr
n n1 n2 nr

15.

Для оценки меры расхождения n и n рассматривают
следующую статистику критерия :
2
2
r
r
(
n
n
)
(
n
N
p
)
ni
2
i
i
i
i
N . (1)
ni
N pi
i 1
i 1
i 1 N pi
r
2
При N данная статистика имеет распределение 2
с k r s 1 степенями свободы, где r число интервалов hi
(или значений xi для дискретной случайной величины) выборки ,
s число параметров предполагаемого распределения
оцениваемых по выборке.

16.

По формуле (1) находят 2набл , по заданным k и из
соответствующей таблицы находят 2 ,k . Тогда ,
если 2набл 2 ,k , то принимают H 0 ;
если 2набл 2 ,k , то H 0 отвергают.
Необходимым условием применения критерия Пирсона
является ni 5 (i 1, r ). Если в отдельных интервалах это не
выполняется, то такие интервалы объединяют с соседними.

17.

Пример. Проведены измерения 100 обработанных деталей.
Отклонения от заданного размера приведены в таблице :
[ xi , xi 1 ) [ 3, 2) [ 2, 1) [ 1,0) [0,1) [1,2) [2,3) [3,4) [4,5)
ni
3
10
15
24
25
13
7
3
Проверить при уровне значимости 0,01 гипотезу H 0 о том, что
отклонения от проектного размера подчиняются нормальному
закону распределения.
Число наблюдений в крайних интервалах меньше 5, поэтому
объединим их с соседними. Получим следующий ряд распределения :
[ xi , xi 1 ) [ 3, 1) [ 1,0) [0,1) [1,2) [2,3) [3,5)
ni
13
15
24
25
13
10
Случайную величину отклонение обозначим через X .

18.

Для вычисления вероятностей pi необходимо вычислить
параметры, определяющ ие нормальный закон распределения
(a и ). Их оценки вычислим по выборке :
1
x
( 2 13 ( 0,5) 15 4 10) 0,885 0,9,
100
1
DВ
(4 13 0,25 15 16 10) (0,885) 2 2,809,
100
DВ 1,7.
Находим pi (i 1,6). ак как случайная величина X ~ N (a, )
определена на ( , ), то крайние интервалы в ряде
распределения заменяем , соответственно, на ( , 1) и (3, ).
1 0,9
Тогда, p1 P( X 1) 0
0 ( )
1,7
1
0 (1,12) 0,1314.
2

19.

Аналогично получаем : p2 0,1667, p3 0,2258, p4 0,2183,
3 0,9
p5 0,1503, p6 P(3 X ) 0 ( ) 0
1,7
0,5 0 (1,24) 0,1075.
Полученные результаты запишем в следующей таблице :
hi ( ,1) [ 1,0) [0,1) [1,2) [2,3) [3, )
ni
13
15
24
25
13
10
ni 13,14 16,67 22,58 21,83 15,03 10,75
Вычисляем 2набл :
2
2
2
2
n
13
15
10
2
i
100 1,045,
набл
N
10,75
i 1 N pi
13,14 16,67
6
то есть 2набл 1,045.

20.

Находим число степеней свободы. По выборке рассчитаны
два параметра, значит, s 2. Количество интервалов 6, то есть
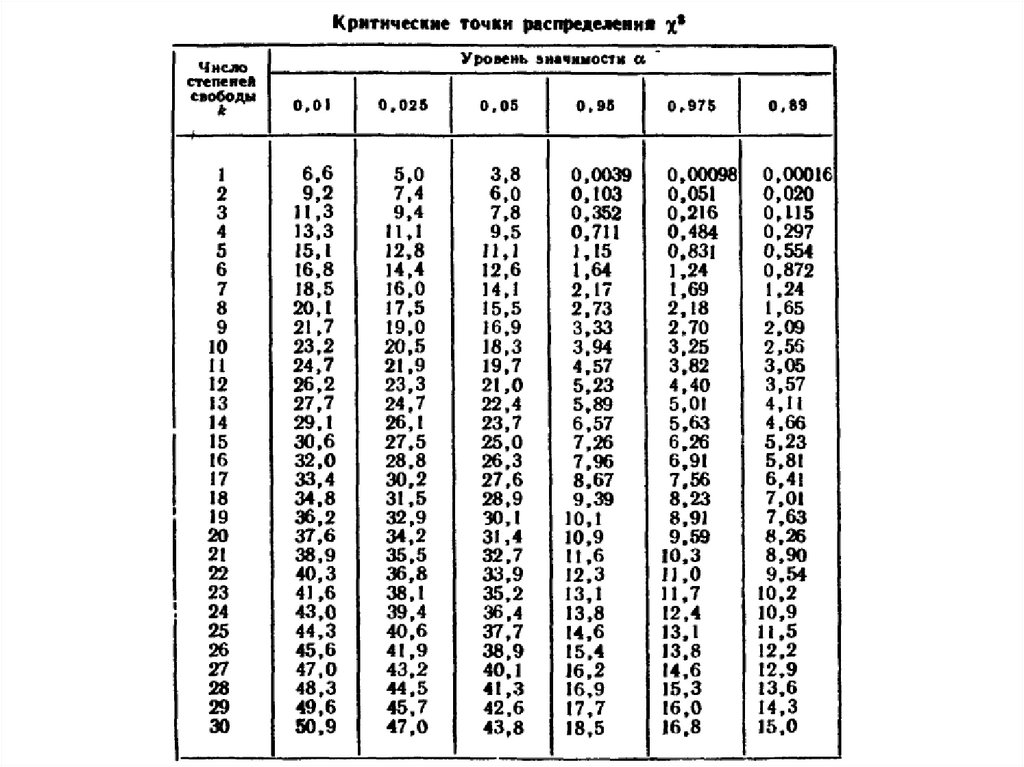
r 6. Следовательно, k 6 2 1 3. Зная, что 0,01 и k 3,
по таблице 2 распределения находим 2 ,k 11,3.
Итак, 2набл 2 ,k , следовательно, нет оснований отвергнуть
проверяему ю гипотезу.

21.

22.

Спасибо за внимание!