Геометрические алгоритмы №6

1.

геометрические алгоритмы
№6

2.

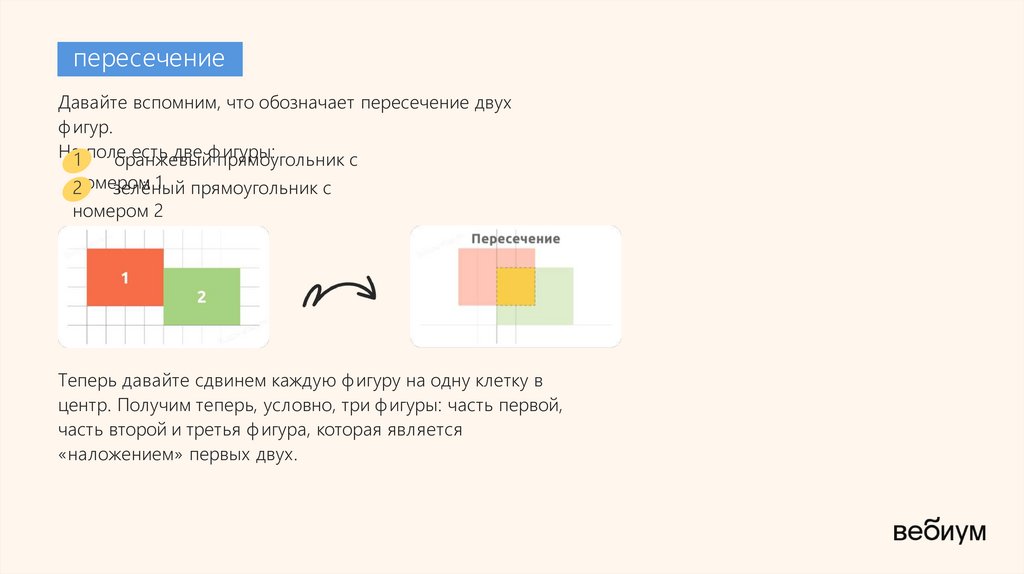
пересечение
Давайте вспомним, что обозначает пересечение двух
ф игур.
На1 поле
есть
две
ф
игуры:
оранжевый прямоугольник с
1
2номером
зелёный
прямоугольник с
номером 2
Теперь давайте сдвинем каждую ф игуру на одну клетку в
центр. Получим теперь, условно, три ф игуры: часть первой,
часть второй и третья ф игура, которая является
«наложением» первых двух.

3.

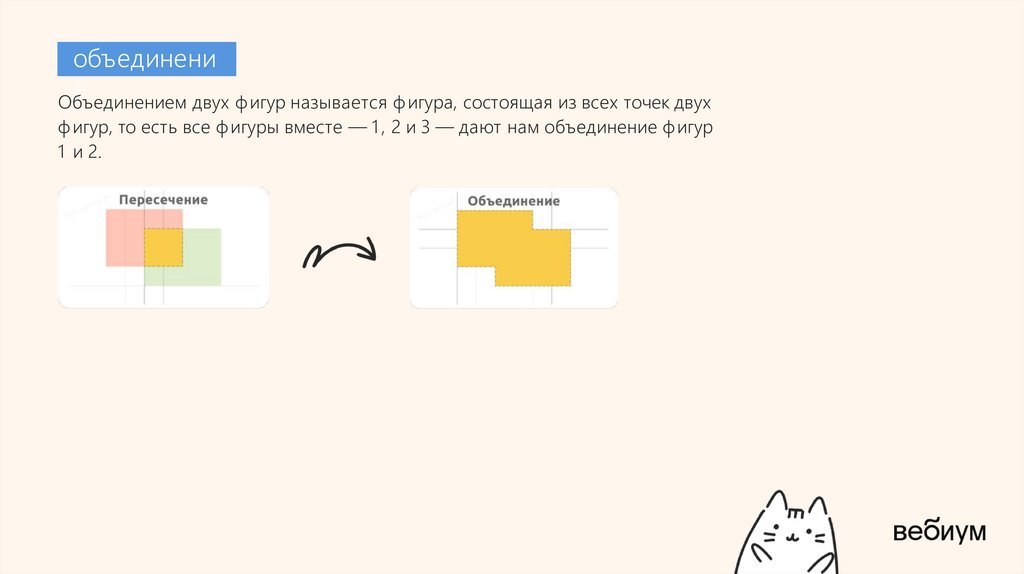
объединени
е
Объединением двух ф игур называется ф игура, состоящая из всех точек двух
ф игур, то есть все ф игуры вместе — 1 , 2 и 3 — дают нам объединение ф игур
1 и 2.

4.

точки на
пересечении
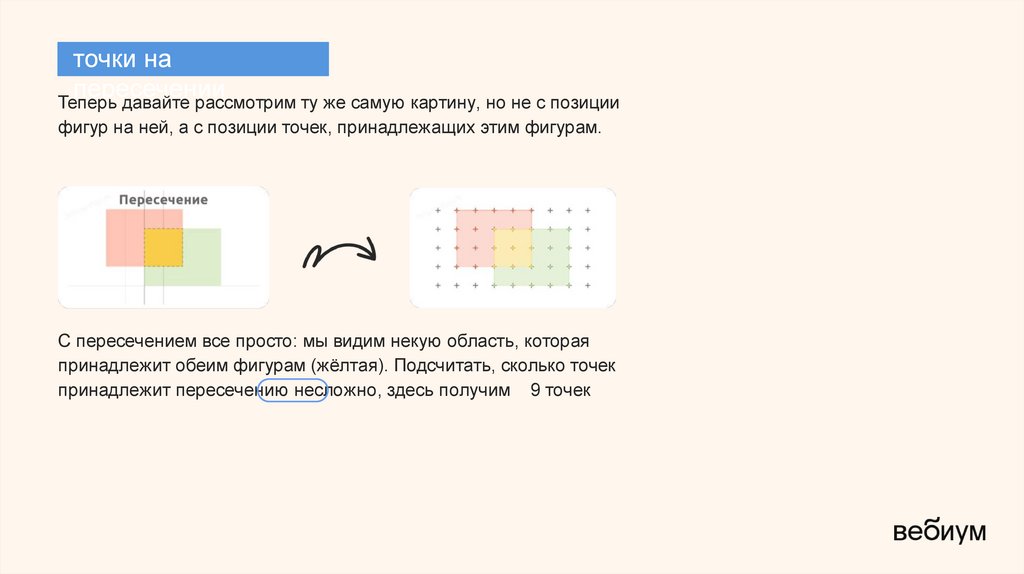
Теперь давайте рассмотрим ту же самую картину, но не с позиции
фигур на ней, а с позиции точек, принадлежащих этим фигурам.
С пересечением все просто: мы видим некую область, которая
принадлежит обеим фигурам (жёлтая). Подсчитать, сколько точек
принадлежит пересечению несложно, здесь получим 9 точек

5.

точки на
объединении
До момента пересечения, у каждой из фигур было по 20 точек (5 на длине и 4 на ширине
прямоугольника). Но после пересечения у каждой из фигур осталось по 11 точек . А вместо 18
точек , которые принадлежали раньше обоим фигурам (по 9 у каждой) теперь осталось только 9,
которые принадлежат пересечению фигур.
Для подсчёта количества точек объединения фигур мы не можем просто сложить количество точек
каждой их этих фигур, ведь мы помним, что у нас есть еще общие точки на пересечении.
Следовательно, необходимо из суммы количества точек этих фигур вычесть количество точек
их пересечения.
Давайте подсчитаем здесь количество точек объединения:
5 · 4 + 5 · 4 – 3 · 3 = 20 + 20 – 9 = 31.

6.

точки не лежат на
линии
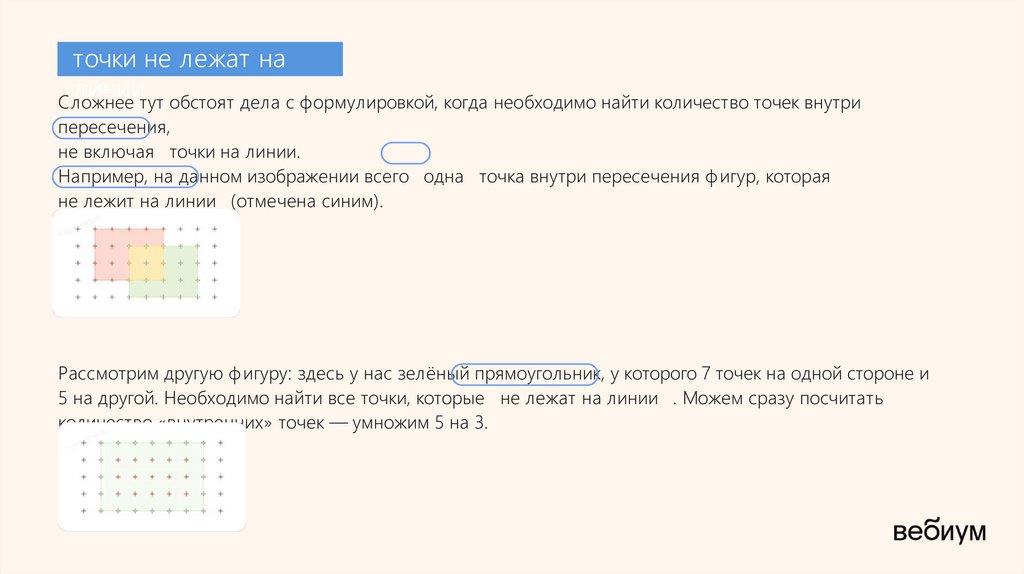
Сложнее тут обстоят дела с формулировкой, когда необходимо найти количество точек внутри
пересечения,
не включая точки на линии.
Например, на данном изображении всего одна точка внутри пересечения ф игур, которая
не лежит на линии (отмечена синим).
Рассмотрим другую ф игуру: здесь у нас зелёный прямоугольник, у которого 7 точек на одной стороне и
5 на другой. Необходимо найти все точки, которые не лежат на линии . Можем сразу посчитать
количество «внутренних» точек — умножим 5 на 3.

7.

точки внутри
объединения
Ряд заданий 6 предполагает нахождение точек внутри объединения.
Разберем тот же самый прямоугольник, у которого 7 точек на одной стороне и 5 на другой. Только
теперь нам важны уже не точки, а отрезки между ними.
Следовательно, отрезков у нас 6 и 4. Значит и длины сторон у нас тоже 6 и 4 единиц.
Тогда площадь найдем перемножив длину одной стороны на длину другой: 6 · 4 = 24.
Периметр находим сложив длины всех стороны: 6 + 4 + 6 + 4 = 20.

8.

пошагово разберём задачу
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент
Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси
ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый
конкретный момент известно положение исполнителя и направление его движения.
У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению без рисования;
Опустить хвост, означающая переход в режим рисования; Вперёд n (где n – целое число), вызывающая
передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n –
целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m –
целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево
m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой
стрелки.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд
повторится k раз.
Черепаха выполнила следующую программу:
Повтори 19 [Вперёд 8 Направо 110 Вперёд 8 Направо 70]
Определите, сколько точек с целочисленными координатами будут находиться внутри области,
ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

9.

1) Начинаем писать программу: импортируем из библиотеки с черепахой все
команды, tracer(0) отключает анимацию рисования черепахи; так как
изначально черепаха смотрит в положительном направлении оси абцисс, то, с
помощью команды left(90), поворачиваем её в сторону положительного
направления оси ординат; screensize() задаёт размеры окна черепахи, тем
самым мы сможем двигать картинку внутри окна также задаём масштаб:
from turtle import *
tracer(0)
left(90)
screensize(5000, 5000)
r = 30

10.

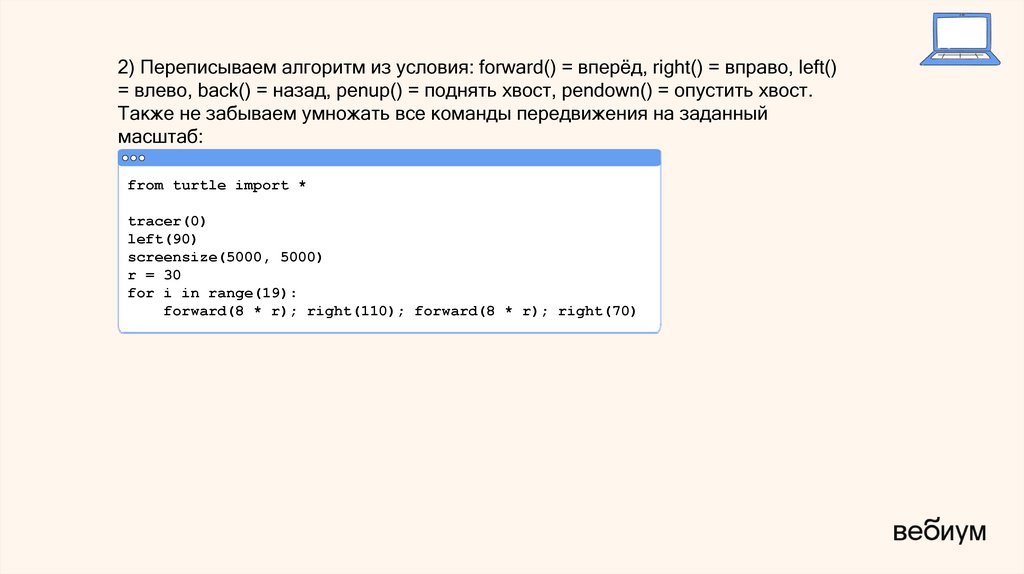
2) Переписываем алгоритм из условия: forward() = вперёд, right() = вправо, left()
= влево, back() = назад, penup() = поднять хвост, pendown() = опустить хвост.
Также не забываем умножать все команды передвижения на заданный
масштаб:
from turtle import *
tracer(0)
left(90)
screensize(5000, 5000)
r = 30
for i in range(19):
forward(8 * r); right(110); forward(8 * r); right(70)

11.

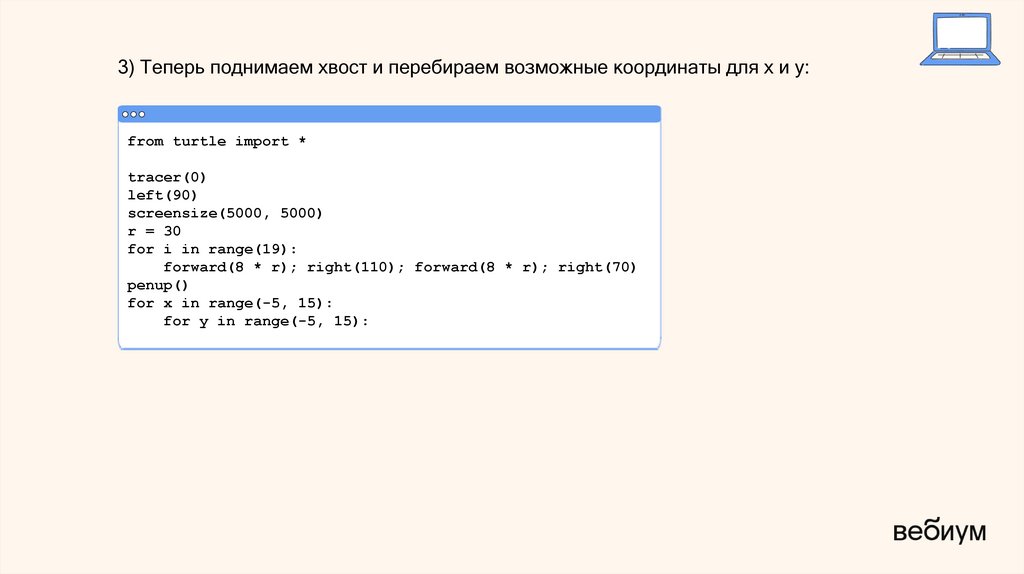
3) Теперь поднимаем хвост и перебираем возможные координаты для x и y:
from turtle import *
tracer(0)
left(90)
screensize(5000, 5000)
r = 30
for i in range(19):
forward(8 * r); right(110); forward(8 * r); right(70)
penup()
for x in range(-5, 15):
for y in range(-5, 15):

12.

4) Ставим черепаху в определенную точку по координатам, с помощью
команды setpose(), не забываем умножать координаты на масштаб. Чтобы
поставить точку используем команду dot(), первый параметр - это размер
точки, второй параметр - цвет точки:
from turtle import *
tracer(0)
left(90)
screensize(5000, 5000)
r = 30
for i in range(19):
forward(8 * r); right(110); forward(8 * r); right(70)
penup()
for x in range(-5, 15):
for y in range(-5, 15):
setpos(x * r, y * r)
dot(3, 'red')

13.

5) При использовании tracer(0) в конце программы обязательно прописываем
команду update(), чтобы картинка черепахи полностью отрисовалась. Также
прописываем команду done(), чтобы окно с черепахой автоматически не
закрывалось, при завершении алгоритма:
from turtle import *
tracer(0)
left(90)
screensize(5000, 5000)
r = 30
for i in range(19):
forward(8 * r); right(110); forward(8 * r); right(70)
penup()
for x in range(-5, 15):
for y in range(-5, 15):
setpos(x * r, y * r)
dot(3, 'red')
update()
done()

14.

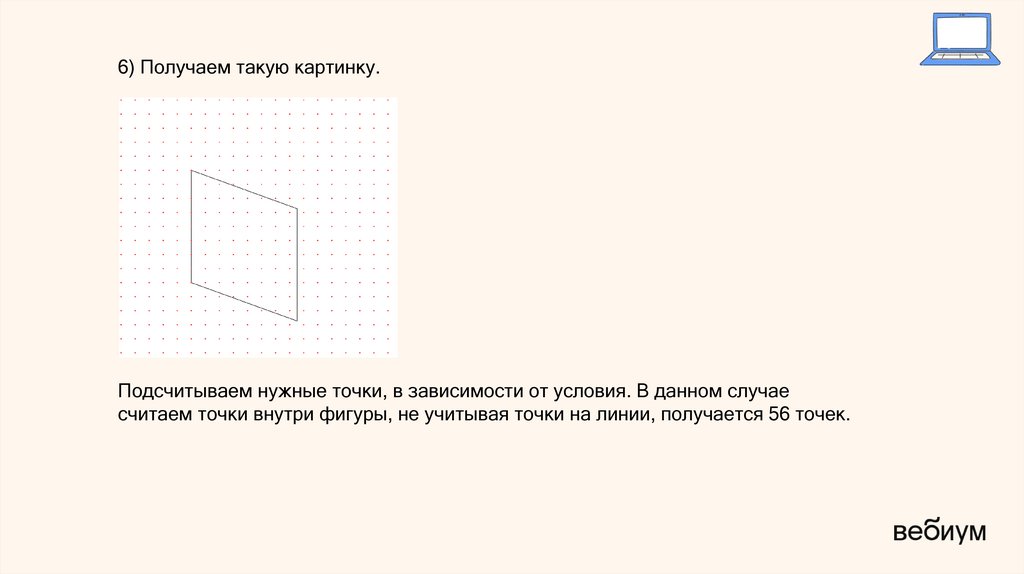
6) Получаем такую картинку.
Подсчитываем нужные точки, в зависимости от условия. В данном случае
считаем точки внутри фигуры, не учитывая точки на линии, получается 56 точек.

15.

простые задачи:
1
2
средняя
сложность:
3
4
5
6
сложные задачи:
7
8

16.

какая ты черепаха сегодня?

17.

1
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В
начальный момент Черепаха находится в начале координат, её голова направлена вдоль
положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха
оставляет на поле след в виде линии. В каждый конкретный момент известно положение
исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том
направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая
изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из
S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 30 Направо 90 Вперёд 12 Направо 90]
Поднять хвост
Налево 270 Вперёд 5 Налево 90
Опустить хвост
Повтори 2 [Вперёд 24 Направо 90 Вперед 28 Направо 90]
В фигуре, получившейся в результате пересечения двух прямоугольников, определите
длину диагонали, которую можно провести из верхней левой точки с целочисленными
координатами в правую нижнюю точку.
пояснение
ответ
25

18.

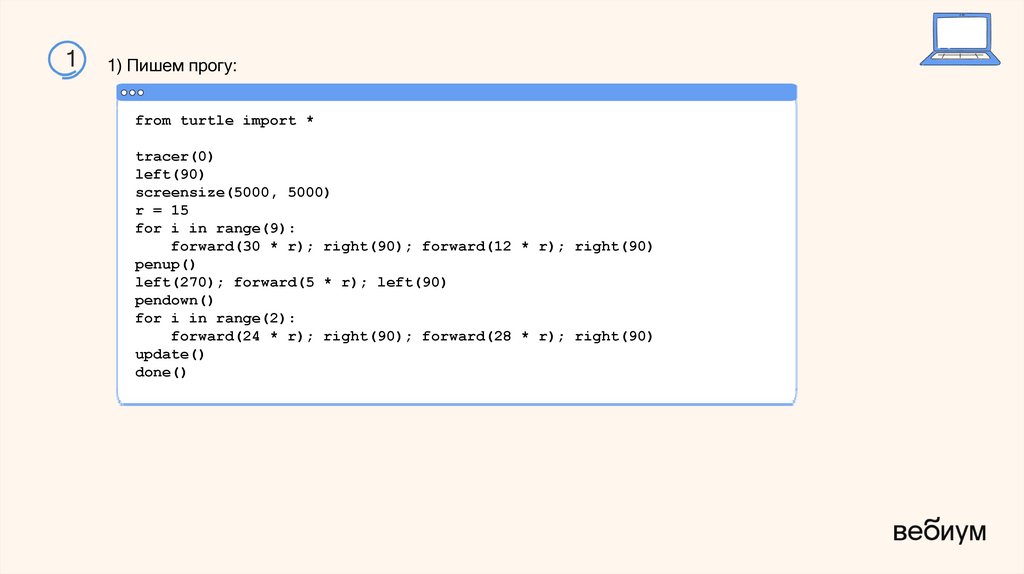
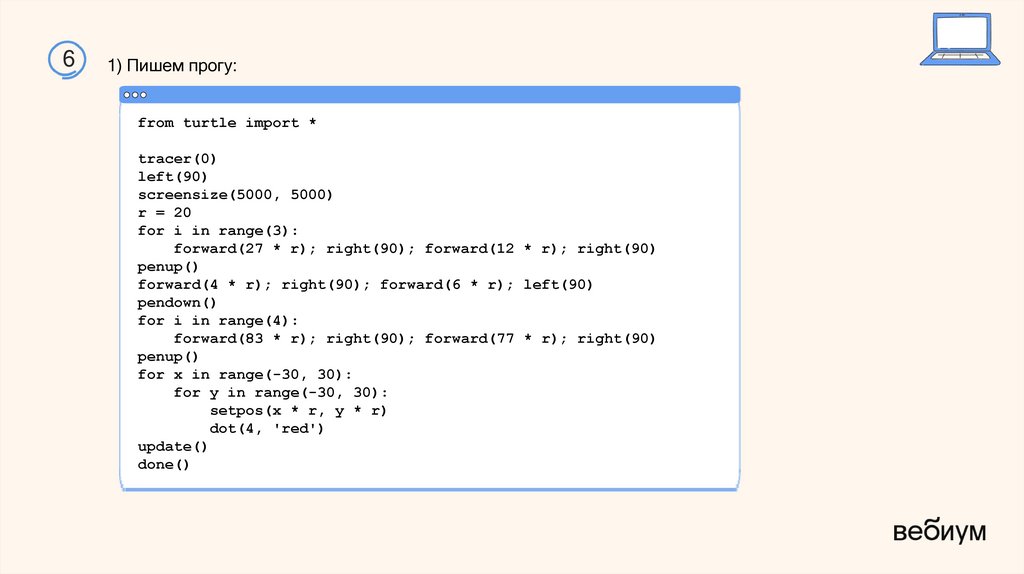
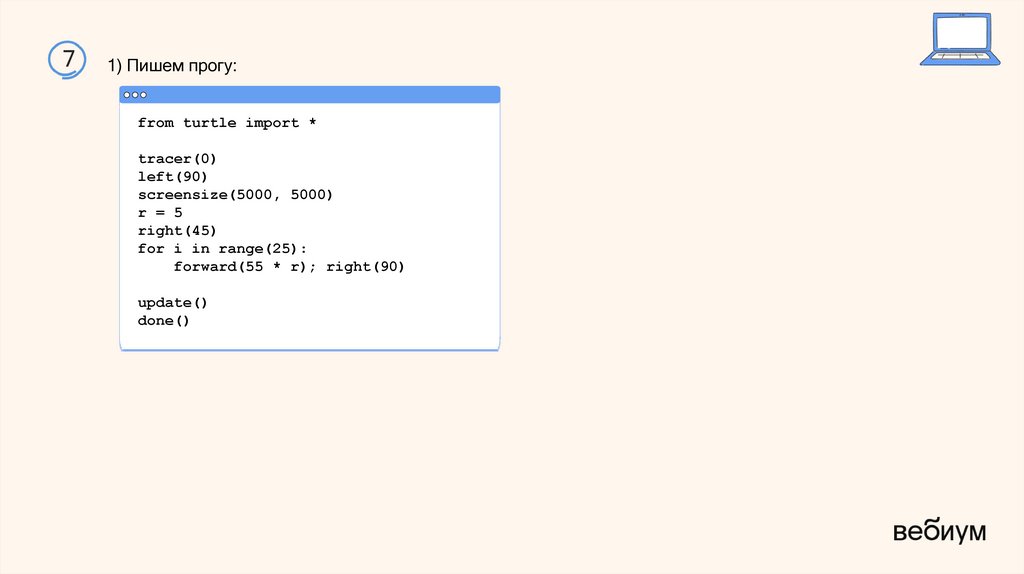
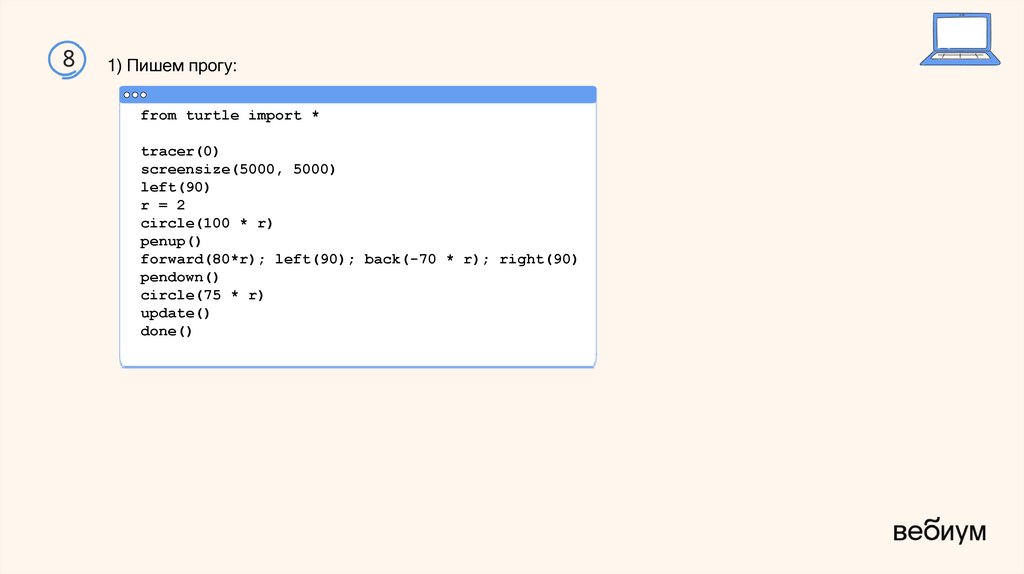
1
1) Пишем прогу:
from turtle import *
tracer(0)
left(90)
screensize(5000, 5000)
r = 15
for i in range(9):
forward(30 * r); right(90); forward(12 * r); right(90)
penup()
left(270); forward(5 * r); left(90)
pendown()
for i in range(2):
forward(24 * r); right(90); forward(28 * r); right(90)
update()
done()

19.

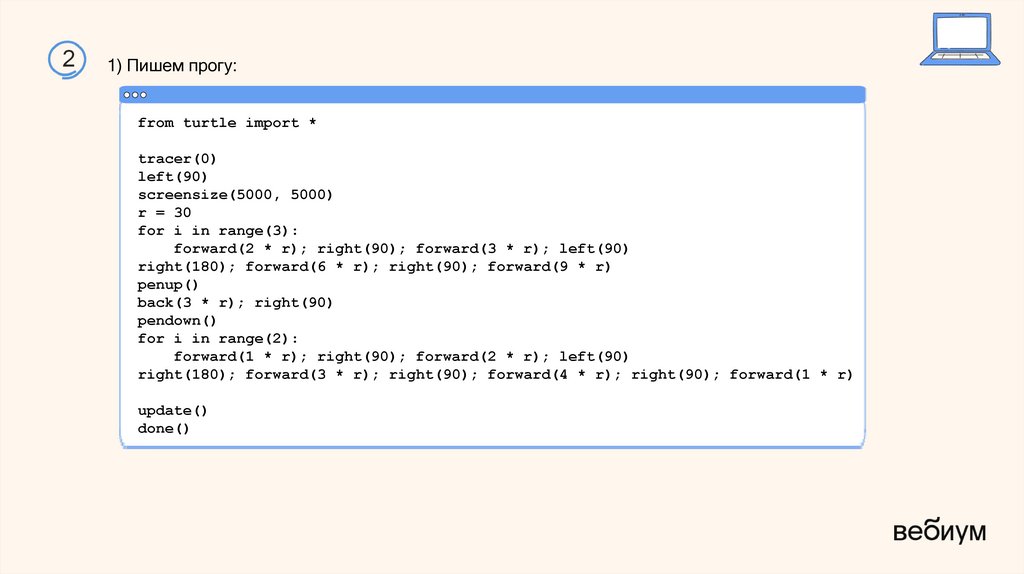
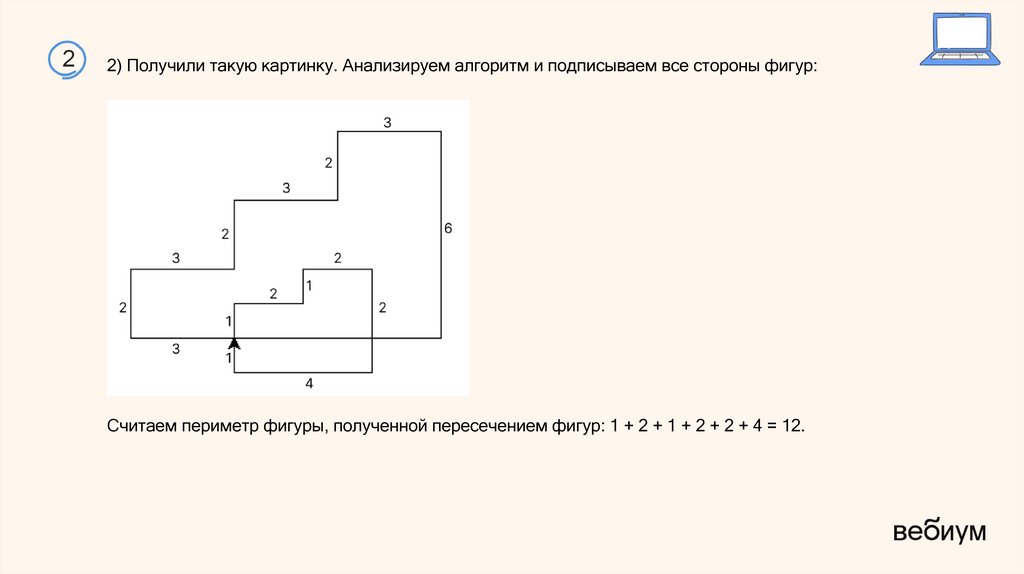
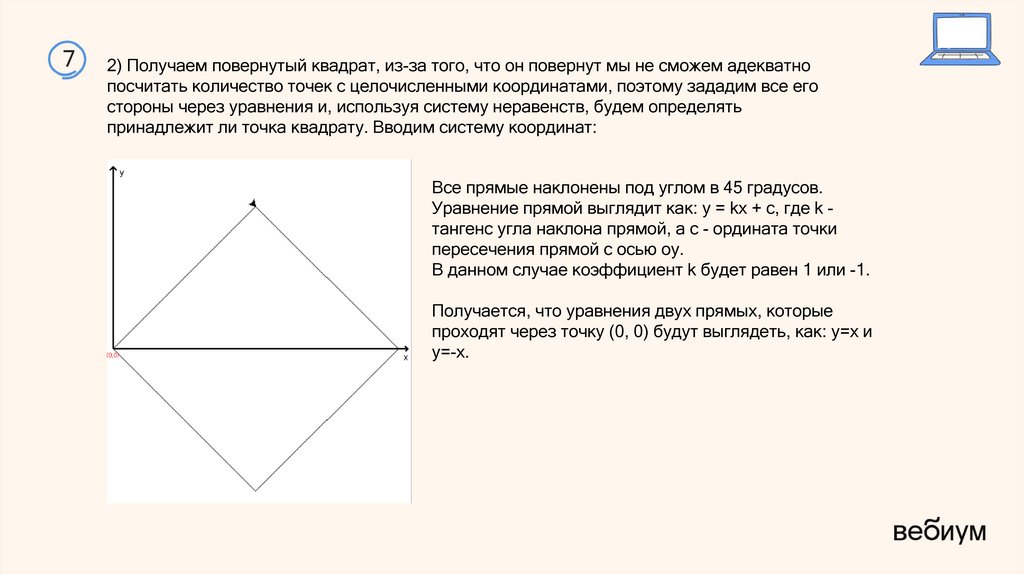
1
2) Получили такую картинку. Анализируем алгоритм, чтобы узнать длины сторон фигур:
Получаем, что стороны прямоугольника, полученного при пересечении фигур 24 и 12 - 5 =
7, находим его диагональ.
По теореме Пифагора находим: