Introduction to Computer Science. Занятие 20. Связные списки. Стек. Очередь. Деревья

1. Introduction to Computer Science

ЗАНЯТИЕ 20

2. Рассматриваемые вопросы

Связные списки
Стек
Очередь
Деревья

3. Связный список

Связный список – линейная, однородная, элементарная
структура данных. Хранит данные одного и того же типа.
Порядок элементов определяется указателями.
Элементы хранятся не обязательно в последовательных
ячейках памяти. Вот почему «связный» – при помощи
указателей разные ячейки (области) памяти связываются
в единое целое.

4. Разновидности связного списка

Односвязный список: каждый элемент – это
запись с данными и указателем на следующий
элемент того же списка.
Двусвязный список – элемент содержит
указатель как на следующий элемент списка,
так и на предыдущий.
Data
Next
Data
Next
Prev

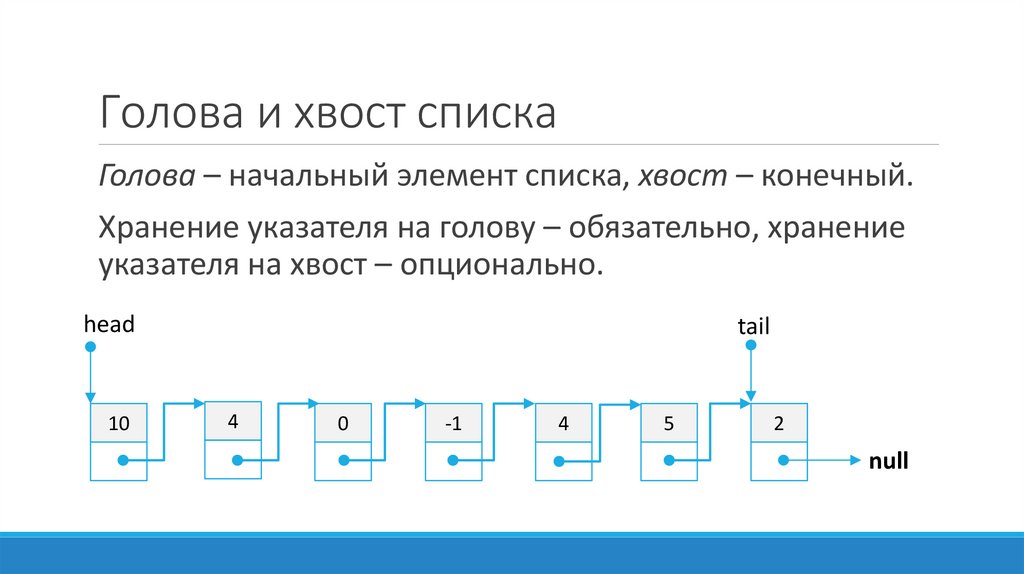
5. Голова и хвост списка

Голова – начальный элемент списка, хвост – конечный.
Хранение указателя на голову – обязательно, хранение
указателя на хвост – опционально.
head
10
tail
4
0
-1
4
5
2
null

6. Стек

Стек - структура данных, в
которой элементы хранятся в
порядке обратном порядку
поступления. LIFO (Last-In/FirstOut) – последним пришел,
первым ушел.
Точка входа/выхода – голова
стека

7. Стек

•вставка элемента
•удаление последнего элемента
•получение значения последнего элемента без удаления
•проверка стека на пустоту

8. Очередь

Очередь - структура данных, в
которой элементы хранятся в
порядке
поступления.
FIFO
(First-In/First-Out)
–
первым пришел, первым ушел.
Точка входа – хвост, точка
выхода – голова очереди

9. Очередь

•вставка элемента в хвост
•удаление элемента из головы
•проверка очереди на пустоту

10. Очередь

•однонаправленная
•двунаправленная

11. Дерево

Корневое дерево – ориентированный
граф со следующими свойствами:
1) есть ровно одна вершина, в которую
не входят дуги, – корень дерева;
2) в любую вершину, кроме корня,
входит ровно одна дуга;
3) есть единственный путь от корня к
каждой из вершин дерева.
C
F
G
D
A
B
E

12. Терминология деревьев

«Генеалогическая»:
– родитель, родительская вершина
– ребёнок, дочерние вершины (узлы)
– предки, потомки
– сиблинги
C
F
G
D
A
B
«Ботаническая»:
– корень
– лист (листья)
E

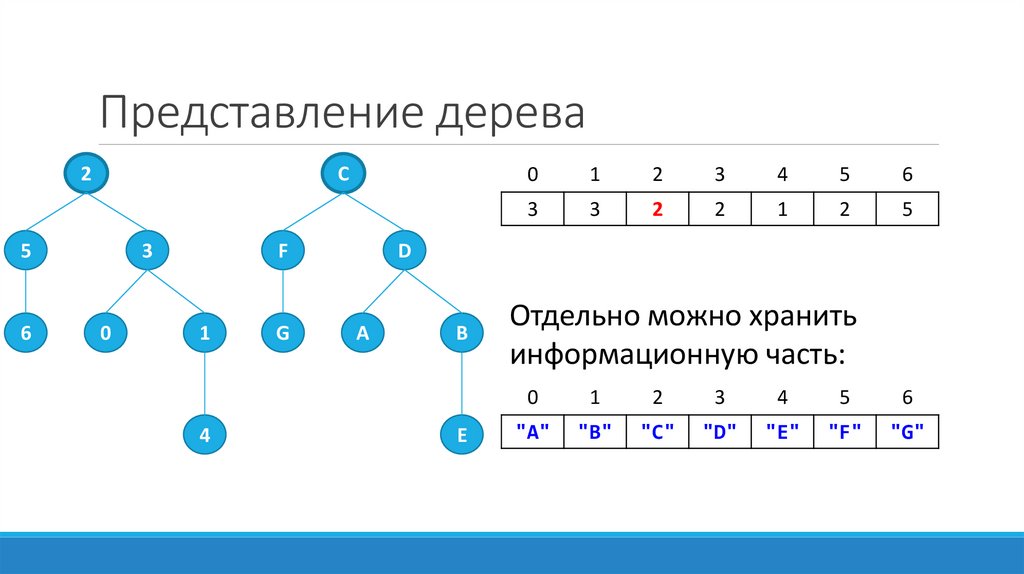
13. Представление дерева

1. Для каждой вершины храним указание на родителя.
«Указание на родителя» – это может быть указатель. А
если вершины пронумеровать – номер родителя.
Последний вариант даёт весьма компактное хранение.
При таком способе хранение по вершине просто искать
родителей и предков. Но сыновей искать не легко!

14. Представление дерева

2
C
5
6
3
0
F
1
4
G
0
1
2
3
4
5
6
3
3
2
2
1
2
5
D
A
B
E
Отдельно можно хранить
информационную часть:
0
1
2
3
4
5
6
"A"
"B"
"C"
"D"
"E"
"F"
"G"

15. Представление дерева

2. Для каждой вершины храним список детей.
Что значит «список»? Это либо связный список, либо
массив (с запасом).
*) Всё упрощается, когда детей фиксированное
количество (например, не больше двух).

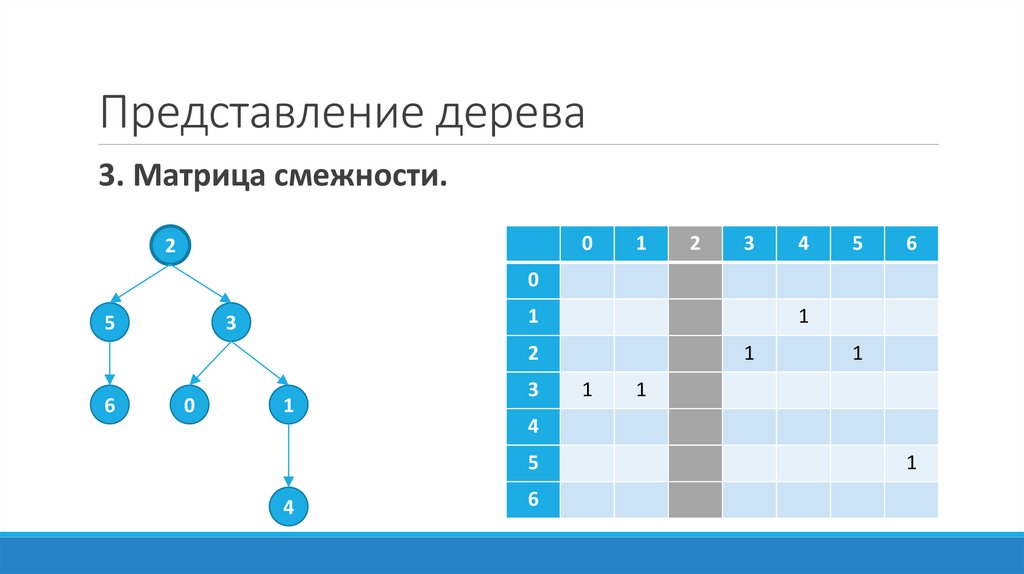
16. Представление дерева

3. Матрица смежности.
0
2
1
2
3
4
5
6
0
5
1
3
1
2
6
0
1
3
1
1
1
4
5
4
1
6
1

17. Бинарное дерево

Бинарное дерево (binary tree) – дерево,
у которого каждый из узлов содержит
не более двух детей с фиксированным
порядком «левый-правый».
5
4
1
7
6
9
8

18. Представление бинарного дерева

Можно с помощью массива (индекс начинается с 1).
Информацию о корне дерева запишем в ячейку