Оптимизация функции потерь градиентным спуском в задаче регрессии

1. Оптимизация функции потерь градиентным спуском в задаче регрессии

Якутов Игорь Вячеславович
02321-ДБ

2. Введение

• Одним из ключевых этапов обучения любой модели
машинного обучения является минимизация функции
потерь — специальной функции, которая
количественно отражает, насколько хорошо модель
справляется с поставленной задачей.
2

3. Цели рассматриваемого эксперимента

FR
· Построить модель множественной линейной регрессии
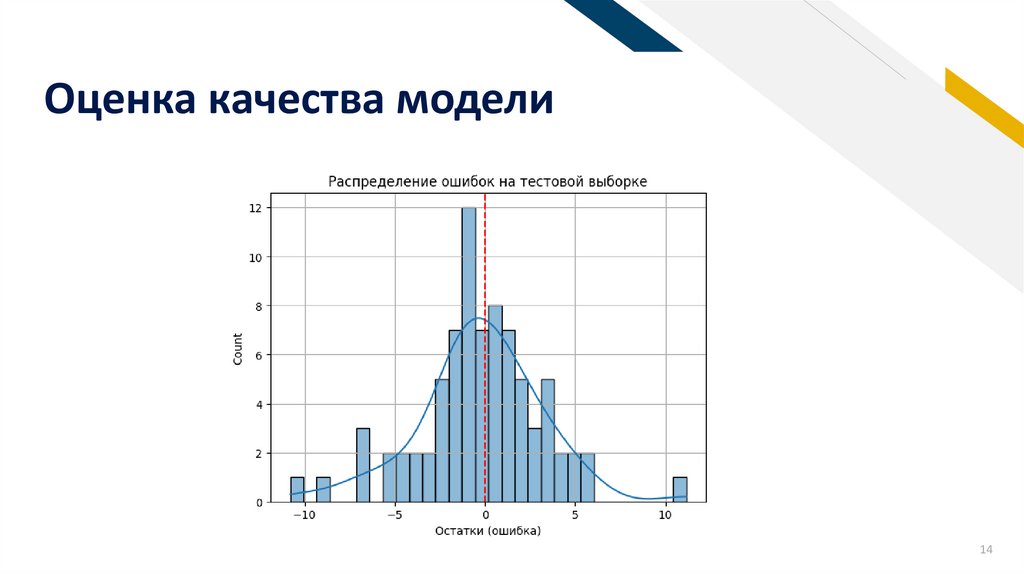
· Оценить качество модели
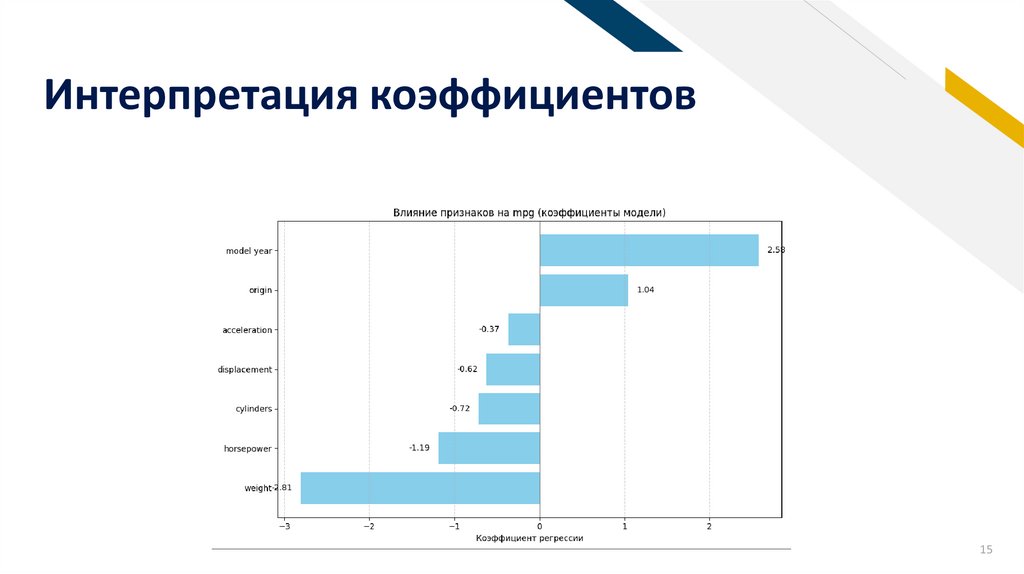
· Интерпретировать полученные коэффициенты
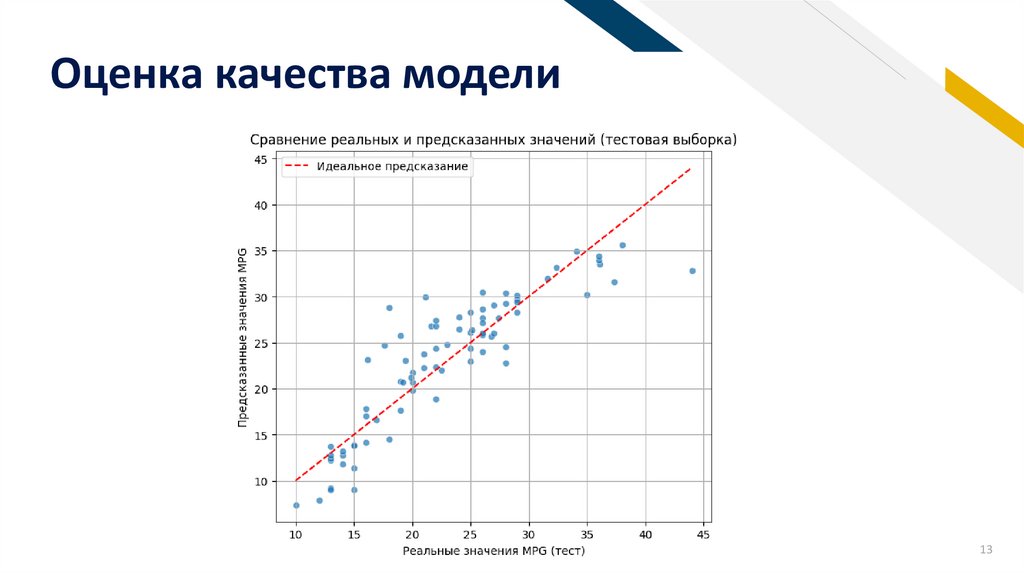
· Сравнить предсказания модели с реальными значениями
3

4. Множественная линейная регрессия

FR
Множественная линейная
регрессия
• yො = w1 x1 + w2 x2 + ⋯ + wn xn + b = w T x + b
• Нужно найти такие параметры w, b, чтобы
предсказание yො было как можно ближе к
фактическому значению y.
4

5.

FR
Функция потерь
Чтобы оценить, насколько хорошо
модель предсказывает значения,
вводится функция потерь.
Наиболее распространённая в
задачах регрессии — это
среднеквадратичная ошибка
(Mean Squared Error, MSE):
n
1
2