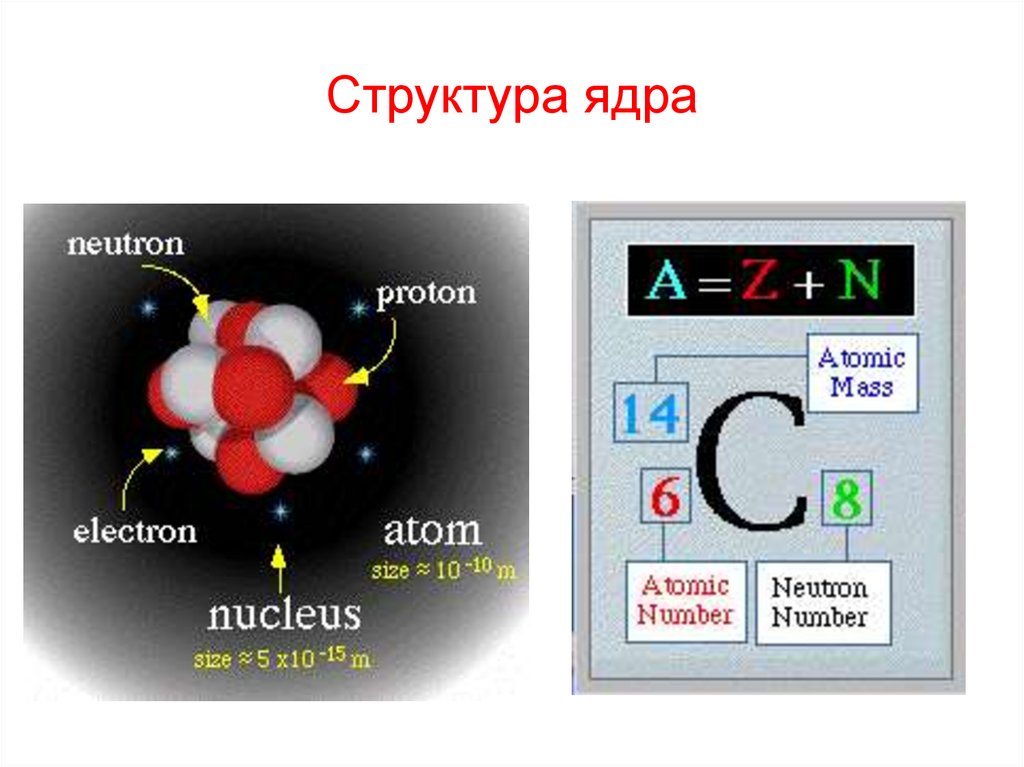
Структура ядра

1.

Структура ядра

2.

Радиоактивность
Радиоактивность – свойство атомных ядер самопроизвольно изменять свой
состав в результате испускания частиц или ядерных фрагментов.
Основными видами радиоактивного распада
являются:
• α-распад – испускание ядрами α-частиц,
• β-распад – испускание (или поглощение)
лептонов,
• γ -распад – испускание γ-квантов,
• спонтанное деление – распад ядра на два
осколка сравнимой массы.
К более редким видам радиоактивного
распада относятся испускание ядрами одного
или двух протонов, а также испускание
кластеров – лёгких ядер от 12С до 32S. Во
всех видах радиоактивности (кроме гаммарадиоактивности) изменяется состав ядра –
число протонов Z , массовое число А или то и
другое одновременно.

3.

N-Z диаграмма атомных ядер

4.

Радиоактивность
Радиоактивный распад может происходить только в том случае, если
масса исходного ядра M i больше суммы масс продуктов распада ∑ M f
Разность
выделяется в виде энергии продуктов распада.

5.

Законы радиоактивного распада ядер
Радиоактивный распад - статистический процесс. Каждое радиоактивное ядро
может распасться в любой момент и закономерность наблюдается только в среднем, в
случае распада достаточно большого количества ядер.
Постоянная распада λ характеризует вероятность распада атомного ядра
в единицу времени.
Если в образце в момент времени t содержится N радиоактивных ядер,
то количество dN ядер, распадающихся в интервал времени t — t+dt, определяется
соотношением («минус» означает, что количество радиоактивных ядер уменьшается
в результате распада)
(1)
Проинтегрировав (1) получим закон радиоактивного распада
(2)
N0 — количество ядер в радиоактивном источнике в начальный момент времени t
= 0,
N(t) — количество радиоактивных ядер, оставшихся в источнике в момент
времени t ,
λ — постоянная распада.
Количество ядер радиоактивного
источника, распавшихся за время t ,

6.

Законы радиоактивного распада ядер
Постоянная распада λ.
Среднее время жизни .
Период полураспада T1/2
— среднее время жизни ядра
T1/2 - период полураспада – время, за которое число радиоактивных
ядер уменьшается вдвое
Связь величин , T1/2 и λ

7.

Законы радиоактивного распада ядер
Активность A - среднее количество ядер распадающихся в единицу времени
A(t) =
N(t).
Активность измеряется в кюри (Ки) и беккерелях (Бк)
1 Ки = 3.7·1010 распадов/c,
1 Бк = 1 распад/c.
Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3,
описывается системой дифференциальных уравнений
dN1/dt = - 1N1
dN2/dt = - 2N2 + 1N1,
где N1(t) и N2(t) -количество ядер, а
соответственно.
1 и 2 - постоянные распада ядер 1 и 2

8.

Законы радиоактивного распада ядер
Решением системы с начальными условиями N1(0) = N10; N2(0) = 0 будет
Если 2 < 1 (
>
), суммарная активность
N1(t) 1 + N2(t) 2 будет монотонно уменьшаться.
Если 2 > 1 (
<
), суммарная активность вначале растет за счет
накопления ядер 2.
Если 2 >> 1, при достаточно больших временах вклад второй экспоненты
становится пренебрежимо мал, по сравнению со вкладом первой
и активности второго A2 = 2N2 и первого изотопов A1 = 1N1 практически
сравняются. В дальнейшем активности как первого так и второго изотопов
будут изменяться во времени одинаково.
A1(t) = N10(t)
1
= N1(t)
1 = A2(t) = N2(t)
2.

9.

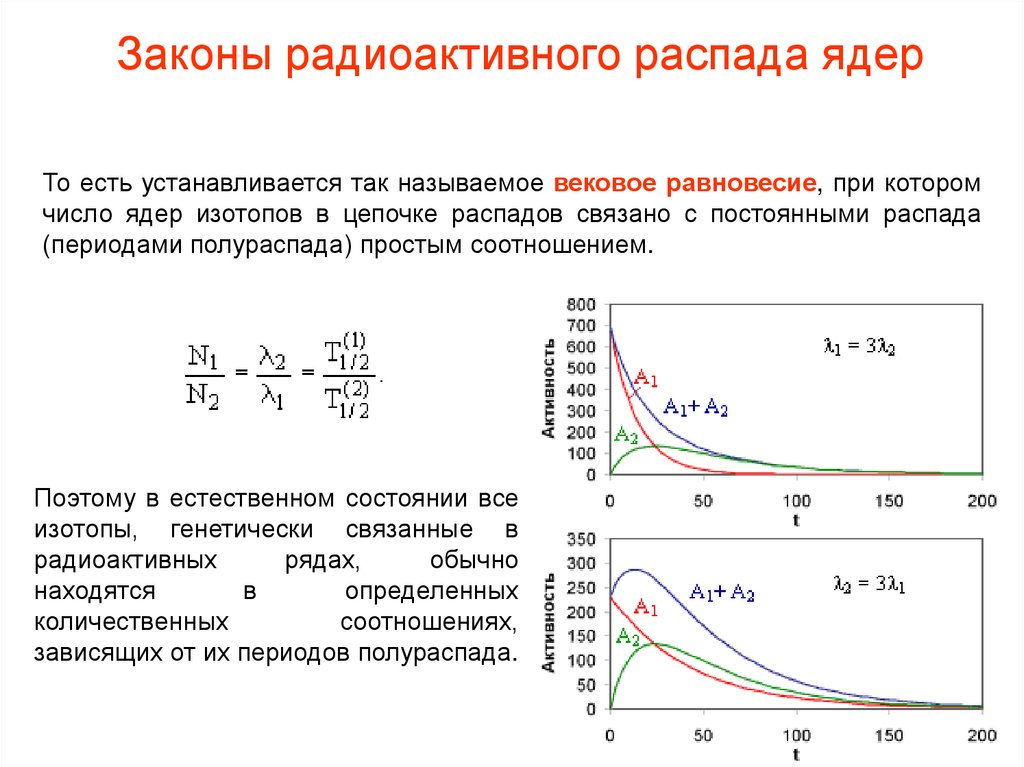
Законы радиоактивного распада ядер
То есть устанавливается так называемое вековое равновесие, при котором
число ядер изотопов в цепочке распадов связано с постоянными распада
(периодами полураспада) простым соотношением.
Поэтому в естественном состоянии все
изотопы, генетически связанные в
радиоактивных
рядах,
обычно
находятся
в
определенных
количественных
соотношениях,
зависящих от их периодов полураспада.

10.

Альфа-распад
Альфа-распад - распад атомных ядер, сопровождающийся испусканием альфа-частиц
(ядер 4He).
Часть изотопов могут самопроизвольно испускать альфа-частицы (испытывать альфараспад), т.е. являются альфа-радиоактивными. Альфа-радиоактивность за редким
исключением (например 8Be) не встречается среди легких и средних ядер. Подавляющее
большинство альфа-радиоактивных изотопов (более 200) расположены в периодической
системе в области тяжелых ядер (Z > 80). Известно также около 20 альфа-радиоактивных
изотопов среди редкоземельных элементов, кроме того, альфа-радиоактивность
характерна для ядер, находящихся вблизи границы протонной стабильности. Это
обусловлено тем, что альфа-распад связан с кулоновским отталкиванием, которое
возрастает по мере увеличения размеров ядер быстрее (как Z2 ), чем ядерные силы
притяжения,
которые
растут
линейно
с
ростом
массового
числа
A.
Ядро альфа-радиоактивно, если выполнено условие, являющееся следствием закона
сохранения энергии
где M(A,Z) и M(A-4,Z-2) - массы покоя
исходного и конечного ядер
соответственно, M - масса альфачастицы.

11.

Альфа-распад
В результате распада конечное ядро и альфа-частица приобретают суммарную
кинетическую энергию
которая называется энергией альфа-распада. Ядра могут испытывать альфараспад также на возбужденные состояния конечных ядер и из возбужденных
состояний начальных ядер. Поэтому соотношение для энергии альфа распада
можно обобщить следующим образом
Q = ( M(A,Z) - M(A-4,Z-2) - M ) с2 +
-
,
где
и - энергии возбуждения начального и конечного ядер соответственно.
Альфа-частицы, возникающие в результате распада возбужденных состояний,
получили название длиннопробежных. Для большинства ядер с A > 190 и для
многих ядер с 150 < A < 190 условие выполняется, однако далеко не все они
считаются альфа-радиоактивными. Дело в том, что современные
экспериментальные
возможности
не
позволяют
обнаружить
альфарадиоактивность для нуклидов с периодом полураспада большим, чем 1016 лет.
Кроме того, часть “потенциально” альфа-радиоактивных ядер испытывают
также бета-распад, который сильно конкурирует с альфа распадом.

12.

Альфа-распад
Основную часть энергии альфа распада (около 98%) уносят альфа-частицы.
Используя законы сохранения энергии и импульса для кинетической энергии
альфа-частицы T можно получить соотношение
252No
Google Play: Isotope Browser (IAEA app)

13.

Альфа-распад
Периоды
полураспада
известных
альфа-радиоактивных
нуклидов
варьируются от 0.298 мкс для 212Po до >1015 лет для 144Nd, 174Hf... Энергия
альфа-частиц, испускаемых тяжелыми ядрами из основных состояний,
составляет 4 - 10 МэВ, ядрами редкоземельных элементов 2 - 4.5 МэВ.
Важным свойством альфа распада является то, что при небольшом
изменении энергии альфа-частиц периоды полураспада меняются на многие
порядки. Так у 232Th Q = 4.08 МэВ, T1/2 = 1.41·1010 лет, а у 218Th Q = 9.85 МэВ,
T1/2 = 10 мкс. Изменению энергии в 2 раза соответствует изменение в периоде
полураспада на 24 порядка.

14.

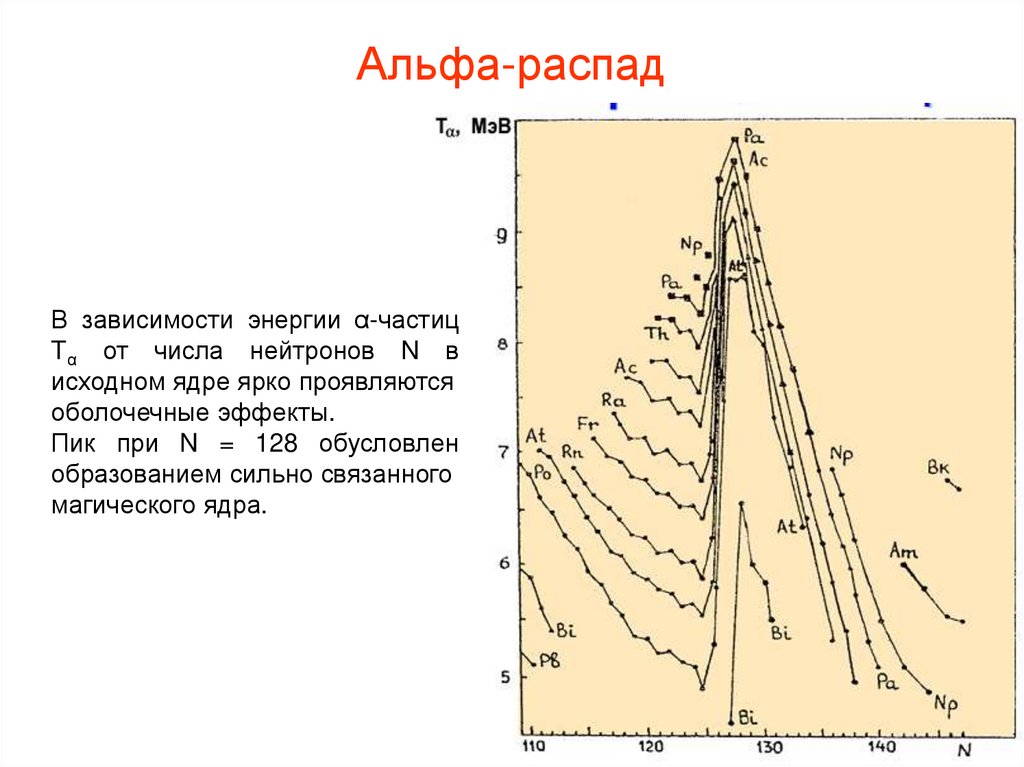
Альфа-распад
В зависимости энергии α-частиц
Tα от числа нейтронов N в
исходном ядре ярко проявляются
оболочечные эффекты.
Пик при N = 128 обусловлен
образованием сильно связанного
магического ядра.

15.

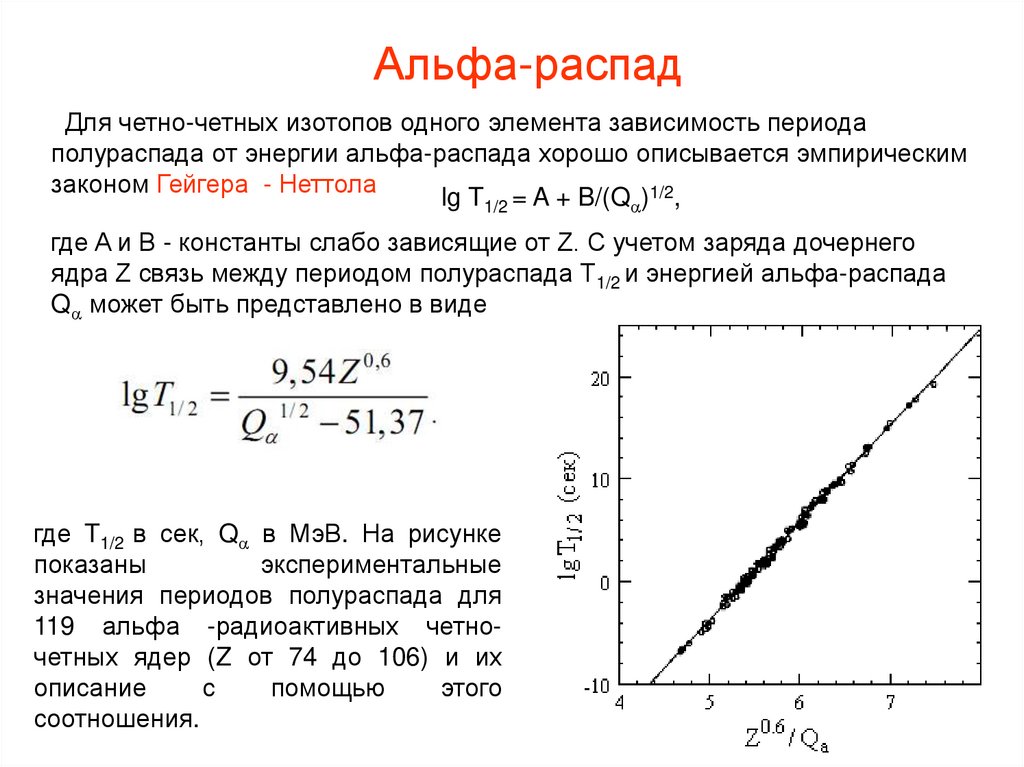
Альфа-распад
Для четно-четных изотопов одного элемента зависимость периода
полураспада от энергии альфа-распада хорошо описывается эмпирическим
законом Гейгера - Неттола
lg T1/2 = A + B/(Q )1/2,
где A и B - константы слабо зависящие от Z. С учетом заряда дочернего
ядра Z связь между периодом полураспада T1/2 и энергией альфа-распада
Q может быть представлено в виде
где T1/2 в сек, Q в МэВ. На рисунке
показаны
экспериментальные
значения периодов полураспада для
119 альфа -радиоактивных четночетных ядер (Z от 74 до 106) и их
описание
с
помощью
этого
соотношения.

16.

Альфа-распад
Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая
тенденция сохраняется, но их периоды полураспада в 2 - 1000 раз больше,
чем
для
четно-четных
ядер
с
данными
Z
и
Q .
Основные особенности альфа-распада, в частности сильную
зависимость вероятности альфа-распада от энергии удалось в 1928 г.
объяснить Г. Гамову и независимо от него Р. Герни и Э. Кондону. Ими было
показано, что вероятность альфа-распада в основном определяется
вероятностью прохождения альфа-частицы сквозь потенциальный барьер.
Рассмотрим простую модель альфа-распада. Предполагается, что
альфа-частица движется в сферической области радиуса R, где R - радиус
ядра. Т.е. в этой модели предполагается, что альфа-частица постоянно
существует
в
ядре.
Вероятность альфа-распада λ равна произведению вероятности
найти альфа-частицу на границе ядра f на вероятность ee прохождения
через потенциальный барьер D (прозрачность барьера)
= fD = ln2/T1/2. (1)

17.

Альфа-распад
Можно отождествить f с числом соударений в единицу времени, которые
испытывает альфа-частица о внутренние границы барьера, тогда
(2)
где v, T , - скорость внутри ядра, кинетическая энергия и приведенная
масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение
V0 = 35 МэВ, T = 5 МэВ, получим для ядер с A
200, f 1021 с-1.
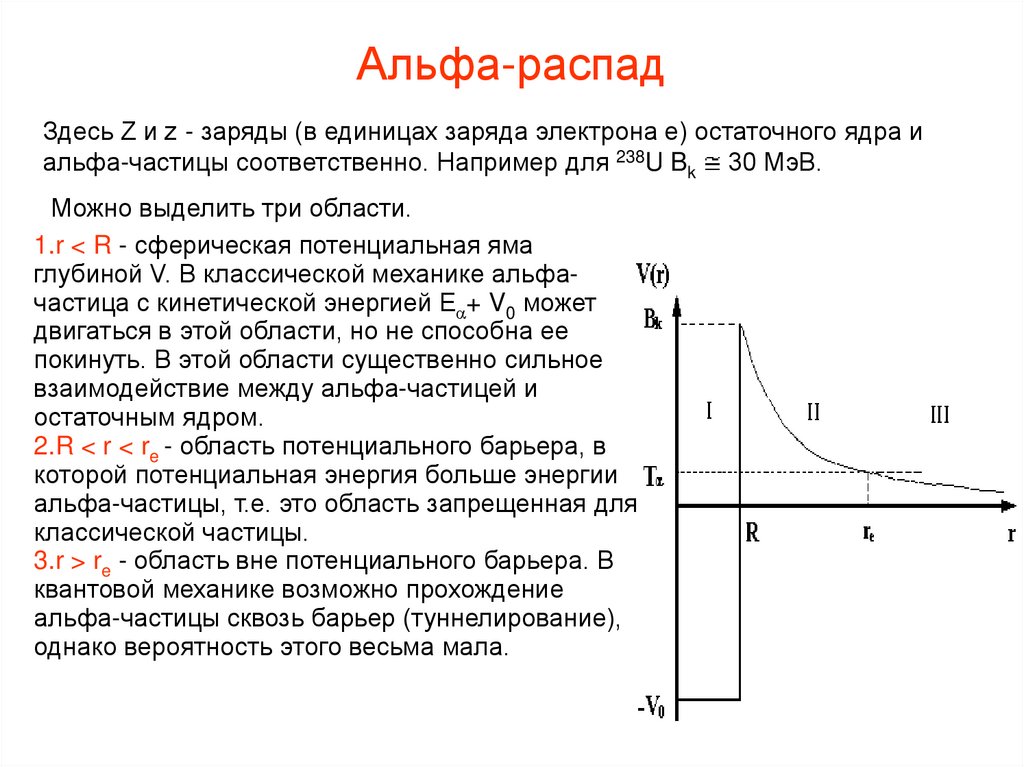
Hа рисунке показана зависимость потенциальной энергии между альфачастицей и остаточным ядром от расстояния между их центрами.
Кулоновский потенциал обрезается на расстоянии R, которое
приблизительно равно радиусу остаточного ядра. Высота кулоновского
барьера Bk определяется соотношением

18.

Альфа-распад
Здесь Z и z - заряды (в единицах заряда электрона e) остаточного ядра и
альфа-частицы соответственно. Например для 238U Bk 30 МэВ.
Можно выделить три области.
1.r < R - сферическая потенциальная яма
глубиной V. В классической механике альфачастица с кинетической энергией E + V0 может
двигаться в этой области, но не способна ее
покинуть. В этой области существенно сильное
взаимодействие между альфа-частицей и
остаточным ядром.
2.R < r < re - область потенциального барьера, в
которой потенциальная энергия больше энергии
альфа-частицы, т.е. это область запрещенная для
классической частицы.
3.r > re - область вне потенциального барьера. В
квантовой механике возможно прохождение
альфа-частицы сквозь барьер (туннелирование),
однако вероятность этого весьма мала.

19.

Альфа-распад
Квантово-механическое решение задачи о прохождении частицы через
потенциальный барьер дает для вероятности прохождения (коэффициента
прозрачности барьера) D
где - приведенная масса, T - энергия α-частицы. В приближении T << Bk, где
Bk - высота кулоновского барьера (предполагается, что барьер чисто
кулоновский) описывается соотношением
(3)
Рассчитанные по формулам 1,2,3 периоды полураспада правильно передают
важнейшую закономерность альфа-распада - сильную зависимость периода
полураспада T1/2 от энергии альфа-частиц T (энергии альфа-распада Q T
). При изменении периодов полураспада более чем на 20 порядков отличия
экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие
расхождения все же довольно велики.

20.

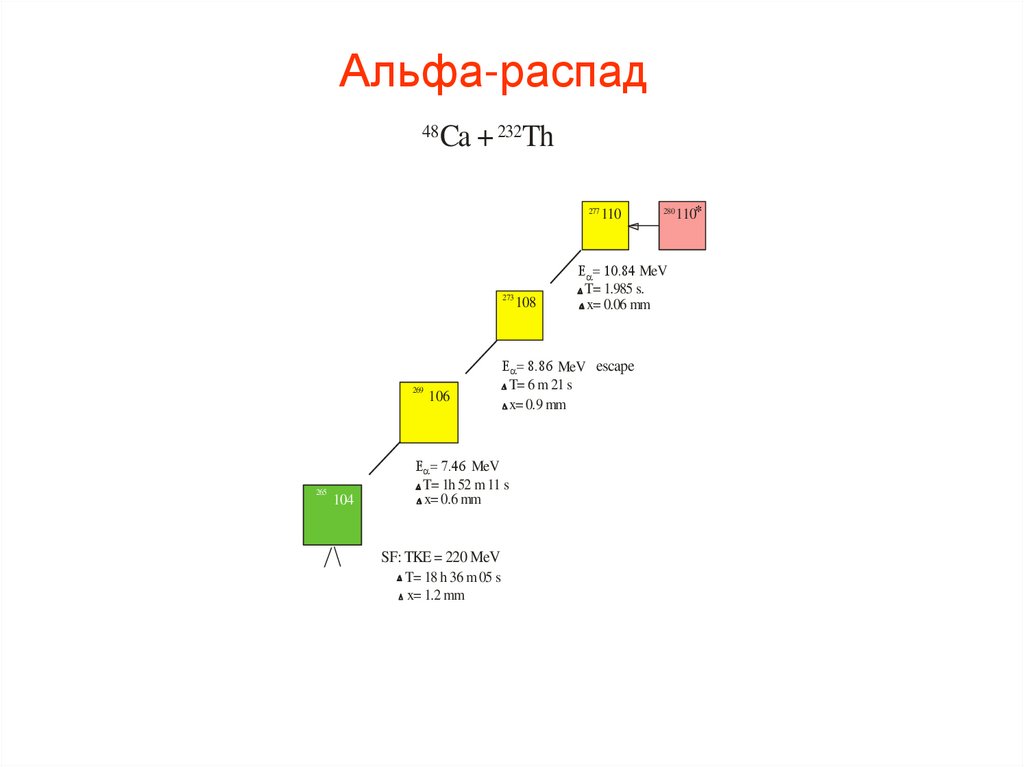
Альфа-распад
48
Ca + 232Th
277
273
269
265
104
106
T= 18 h 36 m 05 s
x= 1.2 mm
280
E = 10.84 MeV
T= 1.985 s.
x= 0.06 mm
E = 8.86 MeV escape
T= 6 m 21 s
x= 0.9 mm
E = 7.46 MeV
T= 1h 52 m 11 s
x= 0.6 mm
SF: TKE = 220 MeV
108
110
110*

21.

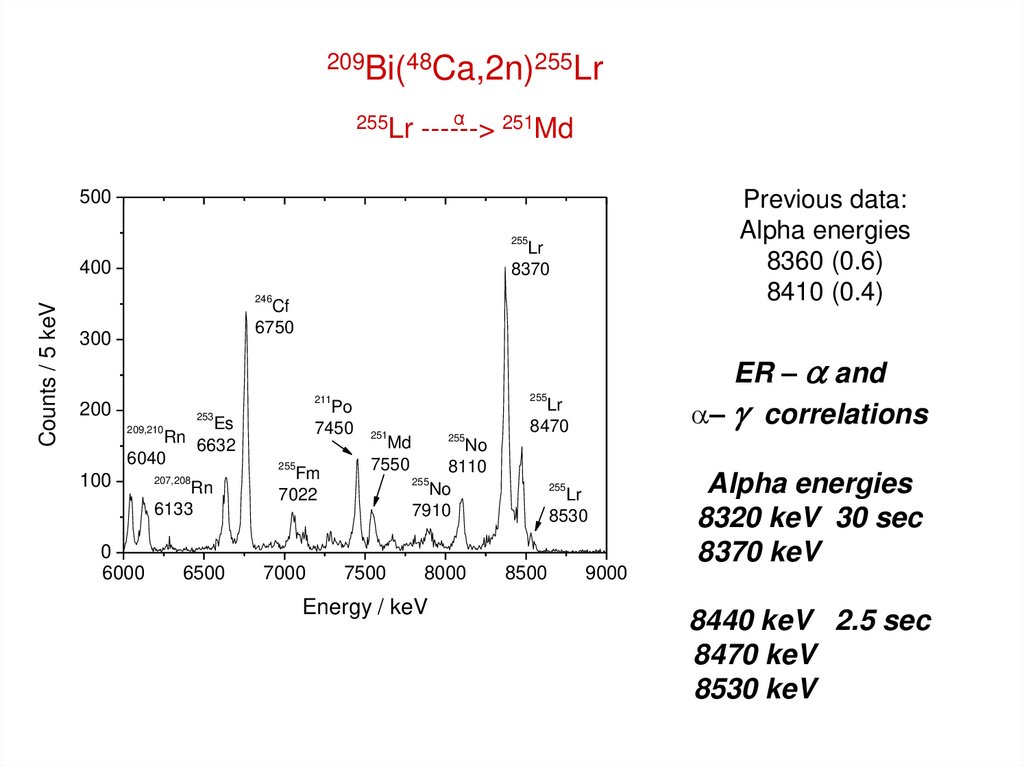
209Bi(48Ca,2n)255Lr
α
255Lr ------>
251Md
500
Previous data:
Alpha energies
8360 (0.6)
8410 (0.4)
255
Lr
8370
Counts / 5 keV
400
246
Cf
6750
300
200
Es
209,210
Rn 6632
6040
100
0
6000
Po
7450
253
207,208
Rn
6133
6500
255
Fm
7022
7000
ER – and
– correlations
255
211
251
Md
7550
7500
255
Lr
8470
No
8110
255
No
7910
8000
Energy / keV
255
Lr
8530
8500
9000
Alpha energies
8320 keV 30 sec
8370 keV
8440 keV 2.5 sec
8470 keV
8530 keV

22.

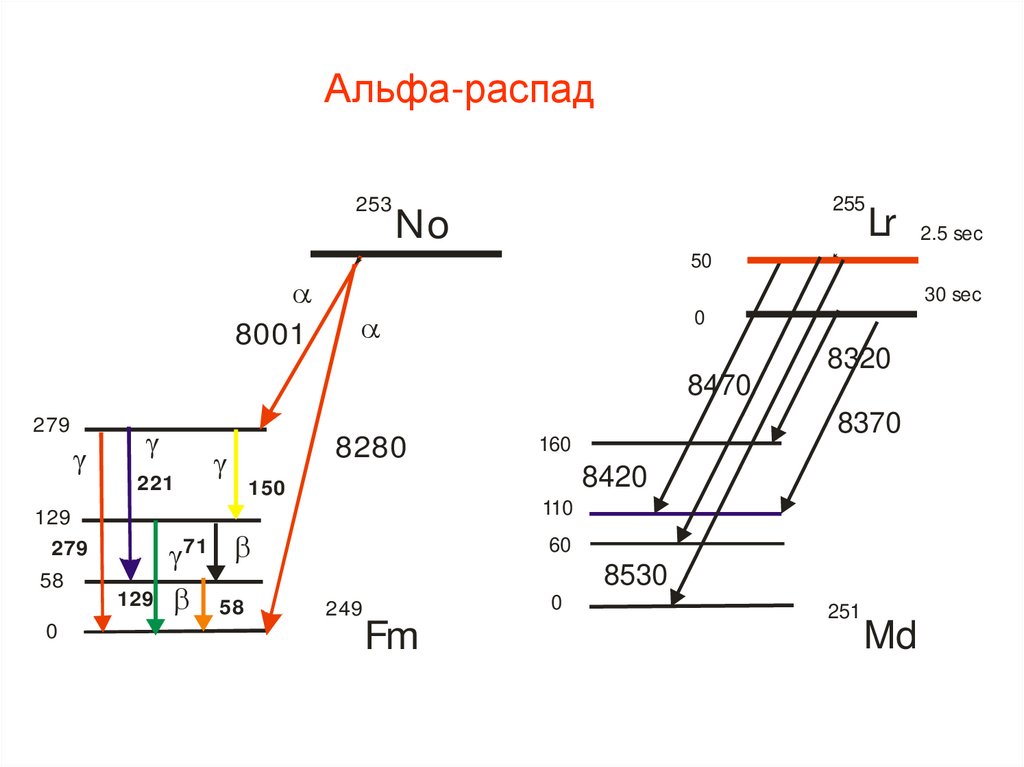
Альфа-распад
При α-распаде конечное ядро может оказаться не только в основном но
и в одном из возбужденных состояний. Распады на возбужденные
состояния приводят к тонкой
структуре
энергетического
спектра
вылетающих α-частиц.
Фактором, способным перераспределить вероятности различных ветвей
альфа-распада, может оказаться необходимость значительной перестройки
внутренней структуры ядра при испускании α-частицы. Если начальное ядро
сферическое,
а
основное
состояние
конечного
ядра сильно
деформировано, то для распада в основное состояние конечного ядра
исходное ядро в процессе испускания α-частицы должно изменить свою
форму. В изменении формы ядра обычно участвует большое число
нуклонов, и такая малонуклонная система, как α-частица, покидая ядро,
может оказаться не в состоянии его обеспечить. Это означает, что
вероятность образования конечного ядра в основном состоянии будет
незначительной. Если же среди возбужденных состояний конечного ядра
окажется состояние близкое к сферическому, то начальное ядро может без
существенной перестройки перейти в него в результате α-распада.

23.

Альфа-распад
Наблюдаются распады на вращательные
уровни, имеющие
относительно низкие энергии возбуждения. Допустимые значения
орбитального
момента
l,
который
может
унести
α-частица,
ограничены законами сохранения момента количества движения и
чётности
Jf и Ji – спины конечного и начального ядер. Из закона сохранения
чётности следует, что значение l должно быть чётным, если чётности
начального и конечного ядер совпадают, и нечётным, если чётности
различны.

24.

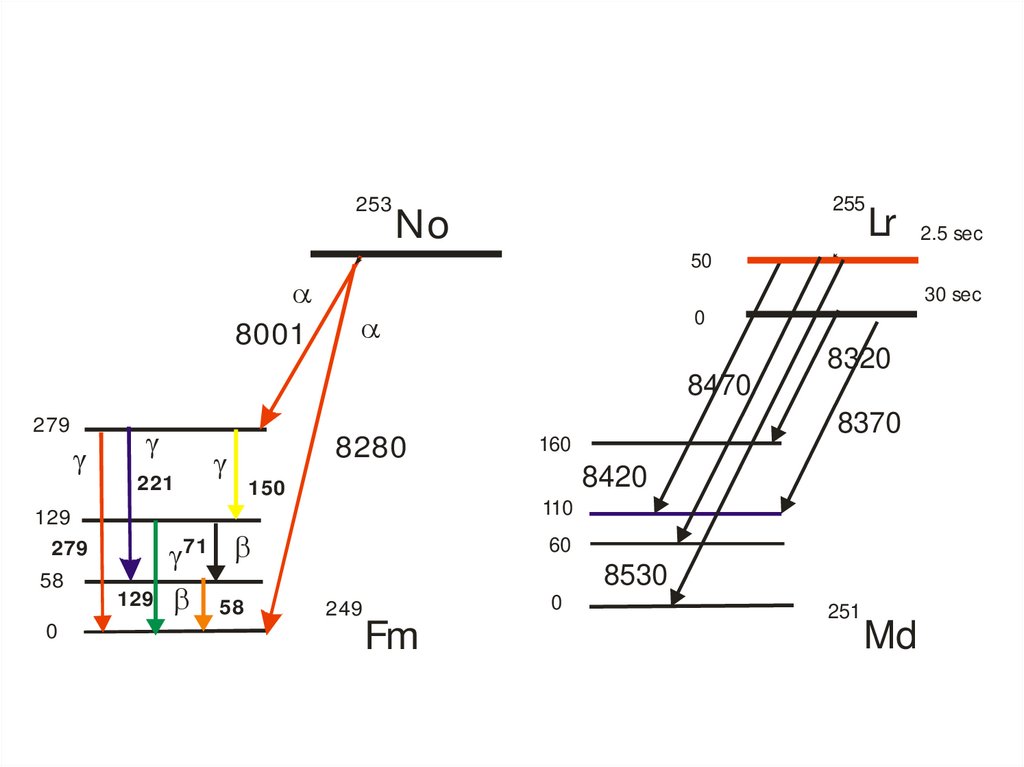
Альфа-распад
253
255
No
Lr 2.5 sec
50
8001
30 sec
0
8470
279
221
129
279
58
0
8280
8320
8370
160
8420
150
110
71 b
129 b 58
60
8530
0
249
Fm
251
Md

25.

Бета-распад

26.

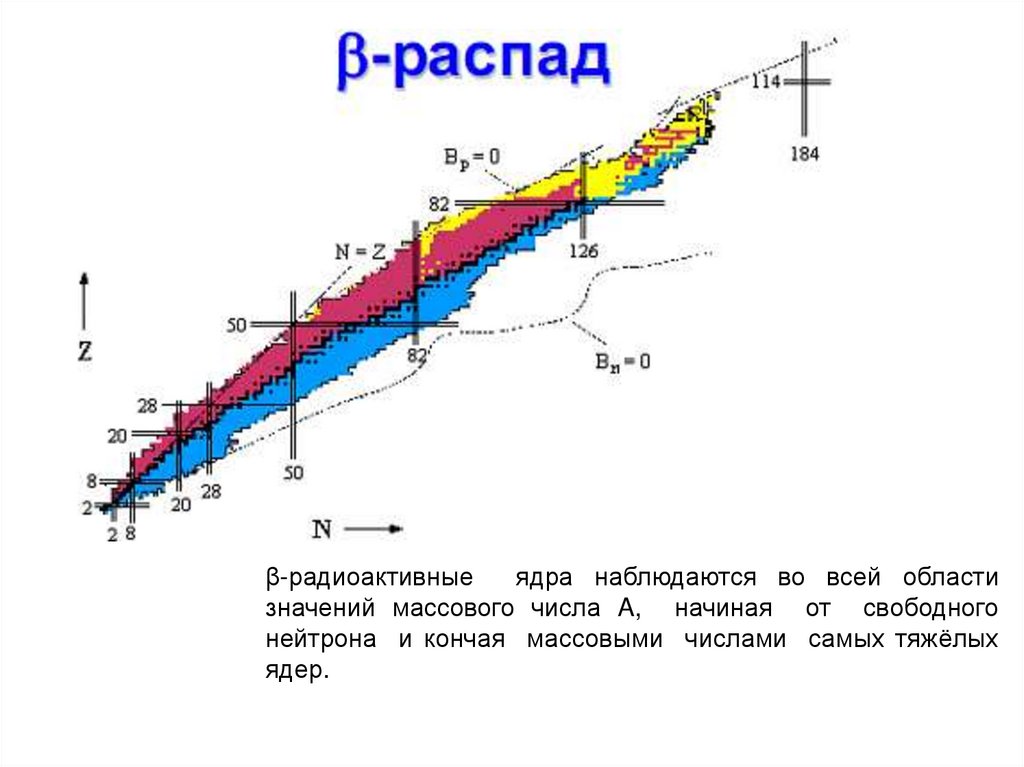
β-радиоактивные
ядра наблюдаются во всей области
значений массового числа A, начиная от свободного
нейтрона и кончая массовыми числами самых тяжёлых
ядер.

27.

28.

Бета-распад
β-распад происходит в результате слабых взаимодействий. На кварковом
уровне при β-распаде происходит превращение d-кварка в u-кварк или
превращение u-кварка в d-кварк. На нуклонном уровне это соответствует
переходам нейтрона в протон или протона в нейтрон.
При этом, если нейтрон может переходить в протон в свободном
состоянии, то превращение протона в нейтрон возможно только для
протонов, связанных в атомном ядре.

29.

Бета-распад
β-распад — внутринуклонный процесс. В ядре распадается одиночный нуклон.
Однако в процессе β-распада происходит перестройка ядра. Поэтому период
полураспада и другие характеристики β-распада в значительной степени
зависят от того, насколько сложна эта перестройка. Массовое число А при βраспаде не изменяется. Стабильные по отношению к β-распаду ядра при всех
А располагаются вокруг значений Zравн с небольшим разбросом в обе стороны
за счет индивидуальных особенностей ядер.
При Z < Zравн ядро нестабильно по отношению к электронному распаду, при
Z > Zравн к позитронному распаду и е- захвату. β-распад часто происходит не
только на основное но и на возбужденные состояния конечного ядра. При
этом в отличие от α-распада энергия возбужденных состояний может быть
сравнимой с полной энергией, выделяющейся при распаде на основное
состояние.

30.

Бета-распад
Бета-распад - спонтанное превращение ядра (A,Z) в ядро-изобар (A,Z+1) в
результате испускания лептонов (электрон и антинейтрино, позитрон и
нейтрино), либо поглощения электрона с испусканием нейтрино (е-захват).
В процессе -распада выделяется энергия
Qβ- = [Mя(A,Z) - Mя(A,Z+1) - me]c2
-
--распад,
Qβ+ = [Mя(A,Z) - Mя(A,Z-1) - me]c2
-
+-распад,
Qе-з = [Mя(A,Z) + me - Mя(A,Z-1)]c2
- е-захват,
где Mя - массы ядер, me - масса электрона. Так как табулируются массы или
избытки масс атомов, то для энергий бета-распадов можно записать
Qβ- = [Mат(A,Z) - Mат(A,Z+1)]c2
-
--распад,
Qβ+ = [Mат(A,Z) - Mат(A,Z-1)]c2 -- 2mec2
-
+-распад,
Qе-з = [Mат(A,Z) - Mат(A,Z-1)]c2
- е-захват
где Mат - массы атомов.

31.

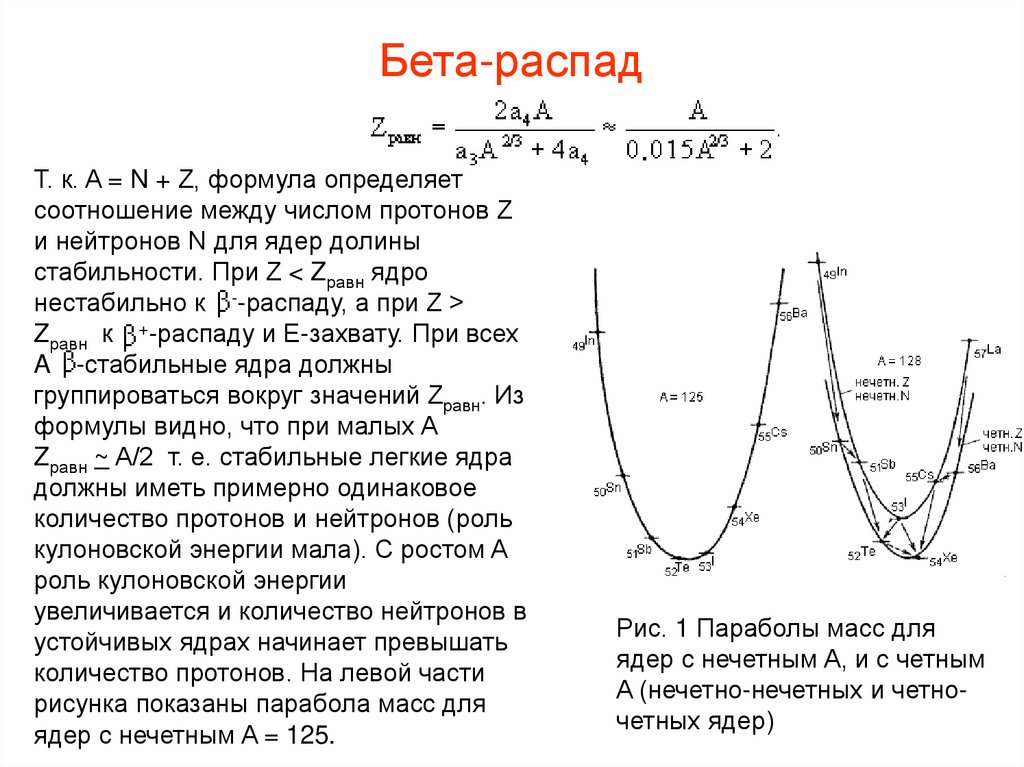
Бета-распад
Т. к. A = N + Z, формула определяет
соотношение между числом протонов Z
и нейтронов N для ядер долины
стабильности. При Z < Zравн ядро
нестабильно к --распаду, а при Z >
Zравн к +-распаду и E-захвату. При всех
A -стабильные ядра должны
группироваться вокруг значений Zравн. Из
формулы видно, что при малых A
Zравн ~ A/2 т. е. стабильные легкие ядра
должны иметь примерно одинаковое
количество протонов и нейтронов (роль
кулоновской энергии мала). С ростом A
роль кулоновской энергии
увеличивается и количество нейтронов в
устойчивых ядрах начинает превышать
количество протонов. На левой части
рисунка показаны парабола масс для
ядер с нечетным A = 125.
Рис. 1 Параболы масс для
ядер с нечетным A, и с четным
A (нечетно-нечетных и четночетных ядер)

32.

Бета-распад
Стабильное ядро 125Te находится в минимуме массовой параболы
(соответственно в максимуме параболы для энергии связи). 125In, 125Sn, 125Sb
подвержены --распаду, 125I, 125Xe, 125Cs, 125Ba - +-распаду. Чем больше энергия
бета-распада ядер (разность масс между соседними изобарами), тем они дальше
от линии стабильности.
Для четных A вместо одной параболы, за счет энергии спаривания (последний
член в формуле Вайцзеккера (1)), получаются две параболы (правая часть
рис.1): для нечетно-нечетных ядер и для четно-четных. Несмотря на то, что
энергия спаривания невелика по сравнению с полной энергией связи ядра (для
ядер с A ~ 100 энергия связи порядка 1000 МэВ, расстояние между параболами
около 2 МэВ), это приводит к важным следствиям. Некоторые нечетно-нечетные
ядра (например 128I) могут испытывать как --распад, так и +-распад и e-захват.
Стабильных четно-четных ядер значительно больше, чем стабильных ядер с
нечетным A и, тем более, чем стабильных нечетно-нечетных ядер, которых всего
четыре (2H, 6Li, 10B, 14N ). При данном A стабильных четно-четных ядер может
быть несколько (например 136Xe, 136Ba, 136Ce). Элементы с нечетным Z редко
имеют больше одного стабильного изотопа, в то время как для элементов с
четным Z это не редкость (112Sn, 114Sn, 115Sn, 116Sn, 117Sn, 118Sn, 119Sn, 120Sn, 122Sn,
124Sn).

33.

Бета-распад
В некоторых случаях, когда для четно-четных ядер невозможен бета-распад
на нечетно-нечетное ядро, оказывается энергетически возможным переход с
изменением Z на две единицы – двойной бета распад. Такой экзотический
распад испытывают 128Te и 130Te. Их содержание в естественной смеси этого
элемента 31.7% и 33.8% соответственно. Вероятность двойного бета-распада
очень мала, периоды полураспада T1/2(128Te) = 7.7*1028 лет, T1/2(130Te) =
2.7*1021 лет.
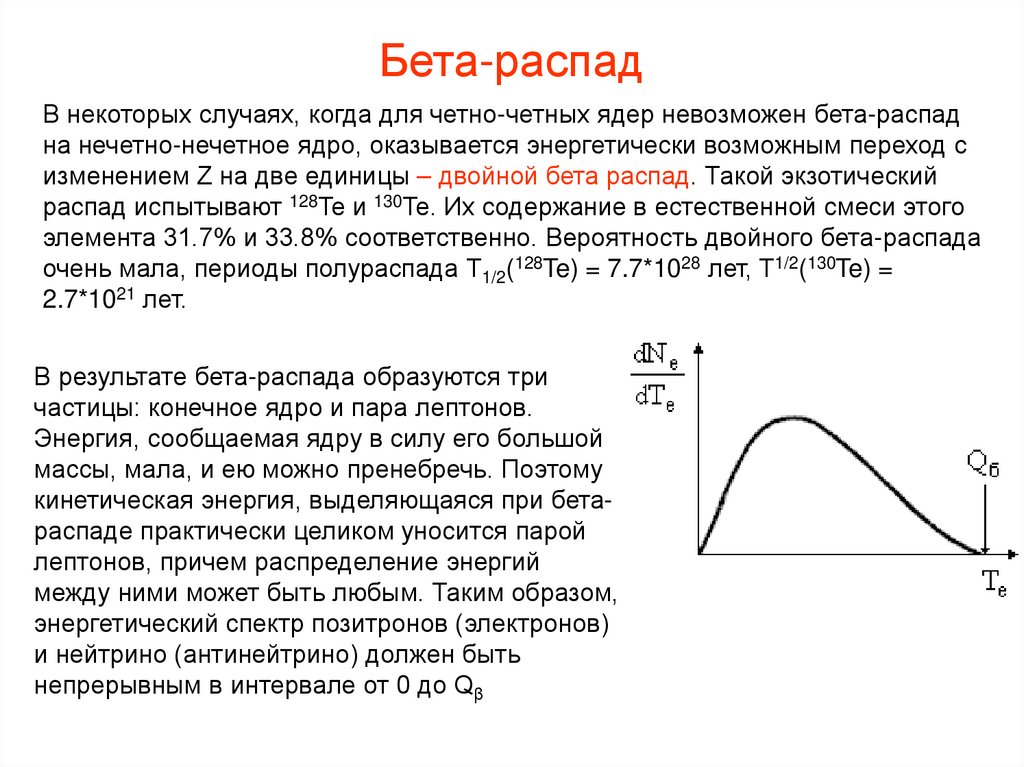
В результате бета-распада образуются три
частицы: конечное ядро и пара лептонов.
Энергия, сообщаемая ядру в силу его большой
массы, мала, и ею можно пренебречь. Поэтому
кинетическая энергия, выделяющаяся при бетараспаде практически целиком уносится парой
лептонов, причем распределение энергий
между ними может быть любым. Таким образом,
энергетический спектр позитронов (электронов)
и нейтрино (антинейтрино) должен быть
непрерывным в интервале от 0 до Qβ

34.

Бета-распад
Вероятность β-распада получается интегрированием β-спектра по энергии. Q
Такая зависимость вероятности β-распада от энергии, выделяющейся
при β-распаде, характерна не только для β-распада, но и для других
слабых распадов и носит название правила Сарджента.

35.

e - захват
Явление е-захвата — захват ядром электрона из
электронной оболочки собственного атома. В случае
захвата ядром орбитального электрона в конечном
состоянии образуются две частицы — конечное ядро и
нейтрино. Так как это двухчастичный распад распределение
энергий между ними является однозначным. Практически
вся она уносится нейтрино. Таким образом, спектр нейтрино
при e-захвате при фиксированных состояниях начального и
конечного ядра будет монохроматическим в отличие от βраспада. В e-захвате участвуют главным образом электроны
ближайших к ядру оболочек (прежде всего К-оболочки). Так
как вероятность взаимодействия с ядром наибольшая для
электронов, расположенных на ближайших к ядру
оболочках, вероятность захвата с К-оболочки будет
максимальной.
е-захват
всегда
сопровождается
рентгеновским излучением, которое возникает в результате
переходов электронов внешних оболочек на вакансию,
образовавшуюся в результате захвата электронов с К- и Lоболочек. е-захват имеет существенное значение в тяжелых
ядрах, в которых К- и L-оболочки расположены близко к
ядру.

36.

Бета-распад
Гипотеза нейтрино была выдвинута В. Паули в 1930 г., чтобы спасти законы
сохранения энергии, импульса и момента количества движения в бетараспаде. Проблема заключалась в том, что, несмотря на вполне
определенные энергии начального и конечного состояний ядер, электроны
бета-распада имели непрерывный спектр. Для объяснения этого Паули
предположил, что наряду с электроном образуется еще одна частица нейтрино, которая уносит часть энергии бета-распада. Паули предсказал
свойства нейтрино. Нейтрино является электрически нейтральной частицей со
спином s = 1/2, с очень маленькой массой и большой проникающей
способностью, т.е. малой величиной сечения взаимодействия с веществом.
Сечение взаимодействия нейтрино (антинейтрино) с энергией несколько
МэВ с веществом ~ 10-43 см2, поэтому для их регистрации необходимы
большие их потоки, большие объемы вещества, в котором происходят
взаимодействия и большое время измерения.
Доказать существование электронного антинейтрино удалось в 1956 г.
Райнесу и Коуэну. Они использовали реакцию
+p
e+ + n.

37.

Бета-распад
В качестве источника антинейтрино был
использован
атомный
реактор.
Образующиеся
в
реакторе
продукты
(осколки) деления как правило β-активны. В
результате β-распада осколков образуется
большое количество антинейтрино, которые
регистрируются с помощью реакции (см.
выше). Протонная мишень представляла из
себя два бака по 200 л каждый, заполненные
раствором хлористого кадмия в воде
(CdCl2+H2O). Возникающие в результате
реакции позитроны регистрировались по
аннигиляционным
γ-квантам,
образующимся
при
взаимодействии
позитронов с электронами вещества мишени.
e+ + e-
2

38.

Бета-распад
Образующиеся в результате аннигиляции -кванты вызывали световые
вспышки в жидких сцинтилляторах (3 емкости по 1200 л каждая),
расположенных по обе стороны от протонных мишеней , которые
регистрировали 100 фотоумножителей. Образующиеся в реакции нейтроны
замедлялись в мишени до тепловых энергий и поглощались кадмием, который
имеет большое сечение захвата тепловых нейтронов (реакция
108Cd(n, )109Cd). Среднее время замедления нейтронов в
водородосодержащей среде ~ 10 мкс. Таким образом для идентификации
антинейтрино регистрировались аннигиляционные -кванты и образующиеся
приблизительно через 10 мкс -кванты из реакции радиационного захвата на
ядрах кадмия.
В результате опытов Райнеса и Коуэна было обнаружено, что антинейтрино
действительно взаимодействует с протоном с образованием в конечном
состоянии нейтрона и позитрона. О сложности выполненного эксперимента
можно судить пол следующим цифрам. В результате первой серии
эксперимента, длившегося 200 часов, было зарегистрировано 567 событий,
вызванных взаимодействием антинейтрино с протоном, при этом фон
составлял 209 событий. Для величины сечения реакции захвата антинейтрино
протоном было получено значение
(
p) = 10-43 см2,
что находилось в хорошем согласии с предварительными теоретическими
оценками.

39.

Бета-распад
Бета-распады разделяются на разрешенные и запрещенные, различающиеся
вероятностями переходов. К разрешенным переходам относятся переходы,
при которых суммарный орбитальный момент l, уносимый электроном и
нейтрино, равен нулю. Запрещенные переходы подразделяются по порядку
запрета, который определяется орбитальным моментом l. Если l = 1, то это
запрещенный переход первого порядка, lmin = 2 - второго порядка и т.д. При
прочих равных условиях отношения вероятностей вылета частицы с
орбитальными моментами
где R - радиус ядра, - длина волны.
Бета-распады также делятся на переходы типа Ферми, при которых спины
вылетающих лептонов антипараллельны, и типа Гамова-Теллера, при
которых спины вылетающих лептонов параллельны.
Вероятность -перехода зависит от энергии -распада приблизительно
как Q5 (правило Сарджента).
Как можно понять такую сильную зависимость вероятности бета-переходов
от орбитального момента вылетающих лептонов?

40.

Бета-распад
На ядро с радиусом R налетает частица с импульсом p и прицельным
параметром b. Классический момент импульса pb равен величине орбитального
момента
pb =
.
Для прицельного параметра b в классическом
приближении должно выполняться условие
b=
/p < R .
Оценим при каких l это условие выполняется. Радиусы даже самых тяжелых
ядер меньше 10 Фм. Для оценки положим радиус равным 10 Фм, а энергию
бета-распада 20 МэВ. Тогда и для электронов мы можем использовать
ультрарелятивистское приближение и переписать предыдущее условие в
виде
c
/T < R
где T - кинетическая энергия вылетающего лептона. Подставив численные
значения, получим
200 МэВ·Фм
/20 МэВ < 10 Фм.

41.

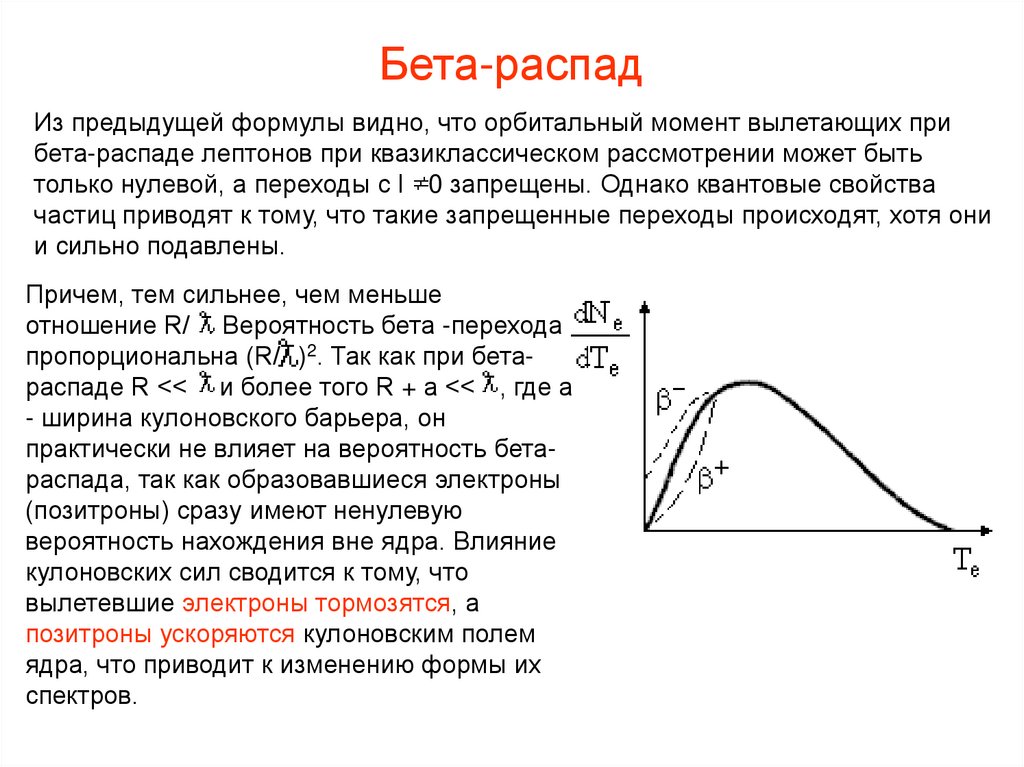
Бета-распад
Из предыдущей формулы видно, что орбитальный момент вылетающих при
бета-распаде лептонов при квазиклассическом рассмотрении может быть
только нулевой, а переходы с l 0 запрещены. Однако квантовые свойства
частиц приводят к тому, что такие запрещенные переходы происходят, хотя они
и сильно подавлены.
Причем, тем сильнее, чем меньше
отношение R/ . Вероятность бета -перехода
пропорциональна (R/ )2. Так как при бетараспаде R << и более того R + а << , где a
- ширина кулоновского барьера, он
практически не влияет на вероятность бетараспада, так как образовавшиеся электроны
(позитроны) сразу имеют ненулевую
вероятность нахождения вне ядра. Влияние
кулоновских сил сводится к тому, что
вылетевшие электроны тормозятся, а
позитроны ускоряются кулоновским полем
ядра, что приводит к изменению формы их
спектров.

42.

Бета-распад
Для разрешенных переходов l = 0. В этом случае волновые функции
лептонов сферически симметричны и поэтому лептоны вылетают в
различных направлениях с одинаковой вероятностью. У запрещенных
переходов волновые функции лептонов уже не являются сферически
симметричными, в силу чего вероятность их вылета в некоторых
направлениях оказывается сильно подавленной.
Правила отбора для полного момента и четности в случае бета-распада
можно записать в виде
где l - суммарный орбитальный момент пары лептонов, Ji, Pi, Jf Pf, - спины и
четности начального и конечного ядер,
- спины лептонов. Вероятность бетапереходов в основном определяется минимальным орбитальным моментом
пары лептонов lmin, удовлетворяющим правила отбора (см. последнее
выражение).

43.

Несохранение четности в слабых
взаимодействиях. Опыт Ву
Подозрения на то, что в слабых взаимодействиях не сохраняется
пространственная четность возникли в связи с наблюдаемыми распадами K+мезонов, которые распадались как на 2, так и на 3 -мезона с нулевыми
относительными орбитальными моментами. Из этого следовало, что четность
K+-мезона в первом случае должна была быть положительной, а во втором
отрицательной. Ли и Янг предложили экспериментально проверить сохранение
четности в слабых взаимодействиях, исследуя -распад поляризованных ядер.
Впервые несохранение пространственной четности в слабых взаимодействиях
было обнаружено в эксперименте Ву и др. в 1957 г. В эксперименте
использовался --активный источник 60Co, помещенный в магнитное поле. У
ядра 60Co величина спина J = 5 и, соответственно, большой магнитный момент,
что позволяло получить достаточно большую степень поляризации ядер в
магнитном поле. Источник 60Co, помещался в магнитное поле кругового тока,
под действием которого спины ядер выстраивались вдоль направления поля.
Для того, чтобы тепловое движение не уничтожило поляризацию 60Co
охлаждался до низкой температуры ~10.0о K. Измерялось количество
электронов -- распада
60Co
60Ni + e- +
e,
испущенных по направлению магнитного поля (спинов ядер) и в
противоположном направлении.

44.

Несохранение четности в слабых
взаимодействиях. Опыт Ву
Вся установка зеркально симметрична относительно плоскости, в которой
расположен круговой ток. При зеркальном отражении импульс (полярный
вектор) меняет направление на противоположное, а напряженность
магнитного поля, магнитный момент, спин (аксиальные вектора) направления
не меняют. Если бы пространственная четность сохранялась, что
эквивалентно зеркальному отражению, одинаковое количество электронов
должно было бы регистрироваться как по направлению магнитного поля, так и
в противоположном направлении. Действительно, закон сохранения
пространственной четности в сферических координатах для квадрата модуля
волновой функции
| (r, ,
)|2 = | (r, - , )|2,
из чего следует, что вероятности найти частицу под углом
и ( - ) равны.

45.

Несохранение четности в слабых
взаимодействиях. Опыт Ву
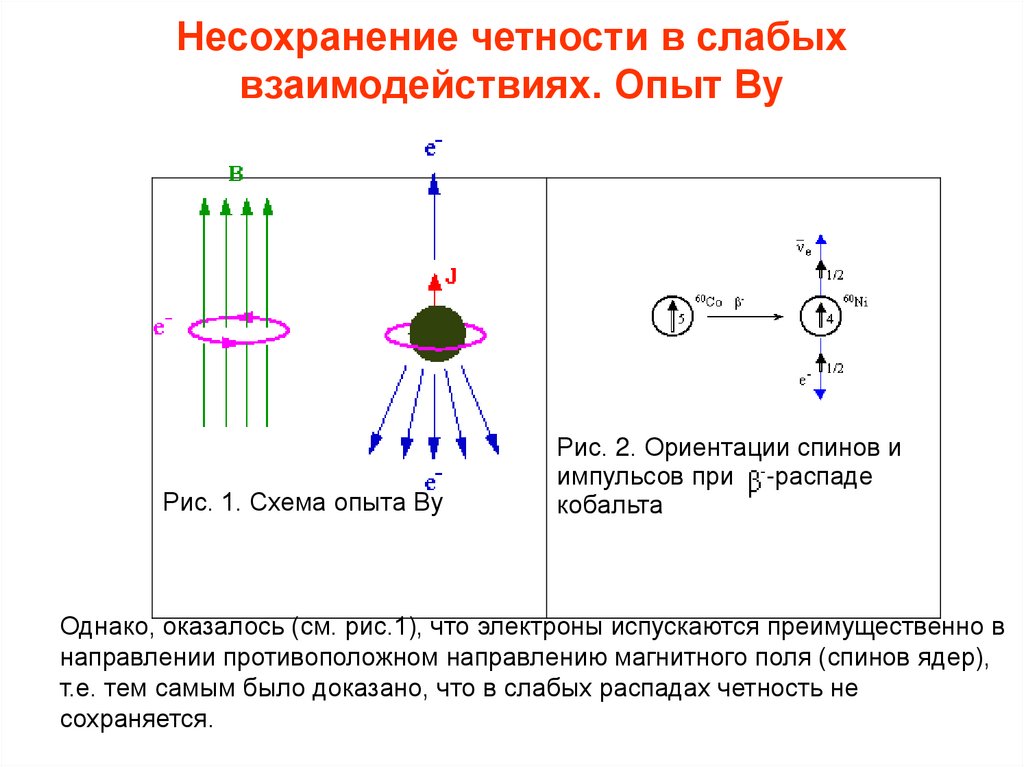
Рис. 1. Схема опыта Ву
Рис. 2. Ориентации спинов и
импульсов при --распаде
кобальта
Однако, оказалось (см. рис.1), что электроны испускаются преимущественно в
направлении противоположном направлению магнитного поля (спинов ядер),
т.е. тем самым было доказано, что в слабых распадах четность не
сохраняется.

46.

Гамма-излучение ядер. Электрические и
магнитные гамма-переходы
Изменения состояний атомных ядер, сопровождающиеся испусканием или
поглощением -квантов, называют -переходами. Примерные границы
периодов полураспада для -переходов от 10-19 с до 1010 лет. Энергии переходов изменяются от нескольких кэВ до нескольких МэВ
Законы сохранения энергии E, момента количества движения (спина) J и
четности P при -переходах в атомных ядрах требуют выполнения следующих
соотношений:
Ei = Ef +
+ TR,
, Pi = PfP,
i =
f+
где Ei, Ef, i, f, Pi, Pf - энергии, спины и четности начального и конечного
состояний ядер,
, P - энергия, спин и четность фотона, TR - кинетическая
энергия ядра отдачи:
где E0 = Ei - Ef - энергия
-перехода, MR - масса ядра отдачи.

47.

Гамма-излучение ядер. Электрические и
магнитные гамма-переходы
Полный момент количества движения фотона J называется
мультипольностью. Значение спина фотона Jmin = 1. Поэтому, полный
момент J уносимый фотоном может принимать целочисленные значения 1, 2,
... (кроме нуля).
Различают электрические (EJ) и магнитные (MJ) переходы. Е1 электрический дипольный переход, М1 - магнитный дипольный переход, Е2 электрический квадрупольный переход и т.д.
Для электрических переходов четность определяется соотношением
P = (-1)J.
Для магнитных переходов P = (-1)J+1.
В случае -переходов большой диапазон периодов полураспада объясняется
сильной зависимостью вероятности -перехода от энергии и мультипольности
переходов. Период полураспада T1/2 -переходов зависит от мультипольности
перехода J и длины волны излучения .
Для электрических
переходов EJ –
для магнитных переходов
MJ -
где R - радиус ядра.

48.

Ядерная изомерия
Изомеры - долгоживущие возбужденные состояния атомных ядер. Сочетание
высокой мультипольности и малой энергии переходов обуславливает
существование состояний с большими периодами полураспада, которые могут
составлять годы. У изотопа может быть несколько изомерных уровней. В
качестве примера можно привести низколежащие уровни изотопа 179Hf. В этом
изотопе обнаружено два изомерных состояния. Одно с энергией возбуждения
375.03 кэВ (JP = 1/2-) и T1/2 = 18.67 c, второе с энергией 1105.63 кэВ (JP = 25/2-)
и T1/2 = 25.1 дня.
У изотопа 178Hf при энергии возбуждения
2446 кэВ имеется изомерное состояние
с (JP = 16+) с периодом полураспада 31
год. Изомерные состояния следует
ожидать в тех областях N и Z, где близко
по энергии расположены оболочечные
состояния сильно различающиеся
значениями спинов.
Причиной ядерной изомерии может
служить также сильное отличие формы
ядра в изомерном и основном состояниях.

49.

Эффект Мессбауэра
Резонансное возбуждение атомных уровней фотонами от источника из того же
вещества легко наблюдается. Иначе обстоит дело для атомных ядер. Это
связано главным образом с тем, что естественная ширина Г ядерных уровней
мала по сравнению с энергией отдачи R ядра-излучателя (источника) или ядрапоглотителя (мишени). Например, естественная ширина Г первого
возбужденного уровня ядра 57Fе, расположенного при энергии возбуждения
E = 14.4 кэВ, равна / = 4.6·10-9 эВ (измеренное среднее время
жизни = 98 нc), тогда как при испускании и при поглощении -квантов это
ядро приобретает энергию отдачи TR ~ Е2/2Мс2 ~ 0.02 эВ (где М - масса атома
57Fе).
Резонансное поглощение может иметь место только в том случае, когда энергия
отдачи ядра R меньше ширины ядерного уровня . Р. Мессбауэр, исследуя
явление резонансного поглощения -квантов понизил температуру источника и
обнаружил, что число поглощенных фотонов существенно увеличилось, то есть
наблюдалось резонансное поглощение -квантов. Качественно это можно
объяснить тем, что в этом случае импульс отдачи получало не отдельное ядро, а
весь кристалл, в котором находились ядра, испускающие -кванты. При
переходе от свободных атомов к атомам, связанным в кристаллической решетке,
ситуация меняется. С уменьшением температуры источника увеличивается
относительное число ядерных переходов с передачей импульса отдачи всему
кристаллу. Условия для этого тем благоприятнее, чем ниже температура
кристалла и энергия перехода

50.

Эффект Мессбауэра
Отмеченное явление, получившее название эффекта Мессбауэра, сразу же
было применено для измерения ширины уровней и для проверки соотношения Г
= / . Чтобы наблюдать резонансное поглощение мишенью из 57Fе -квантов,
испускаемых источником из 57Fе, нужно скомпенсировать энергию отдачи ядра,
которая в сумме составляет 2TR. Если пренебречь естественной шириной
уровня, то энергия испускаемых фотонов равна
= Е - TR, тогда как для того,
чтобы наблюдался резонанс, они должны иметь энергию
= Е + TR. Один из
способов такой компенсации состоит в том, что рассматриваемый
радиоактивный источник закрепляют на движущемся устройстве и подбирают
скорость так, чтобы разница 2TR компенсировалась за счет эффекта Доплера.
Для этого достаточно укрепить исследуемый источник на подвижной каретке и
изменять ее скорость v так, чтобы за счет эффекта Доплера сдвинуть линию
резонансного поглощения в нужную сторону. Между детектором и источником
помещают поглотитель того же изотопического состава, что и источник, как
показано на рис.1. В отсутствие отдачи резонансное поглощение должно
происходить при v = 0. В этом случае число фотонов, регистрируемое
детектором, будет минимально, так как фотоны, претерпевшие резонансное
поглощение в поглотителе, затем повторно испускаются в разных направлениях
и выбывают из прошедшего пучка.

51.

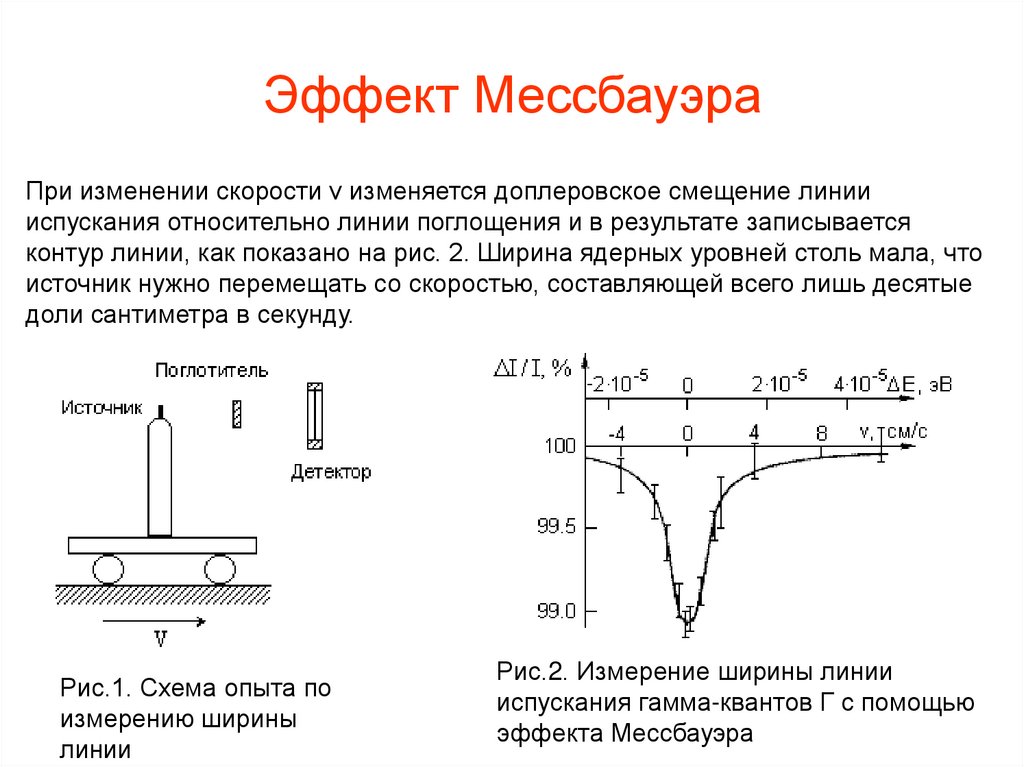
Эффект Мессбауэра
При изменении скорости v изменяется доплеровское смещение линии
испускания относительно линии поглощения и в результате записывается
контур линии, как показано на рис. 2. Ширина ядерных уровней столь мала, что
источник нужно перемещать со скоростью, составляющей всего лишь десятые
доли сантиметра в секунду.
Рис.1. Схема опыта по
измерению ширины
линии
Рис.2. Измерение ширины линии
испускания гамма-квантов Г с помощью
эффекта Мессбауэра

52.

53.

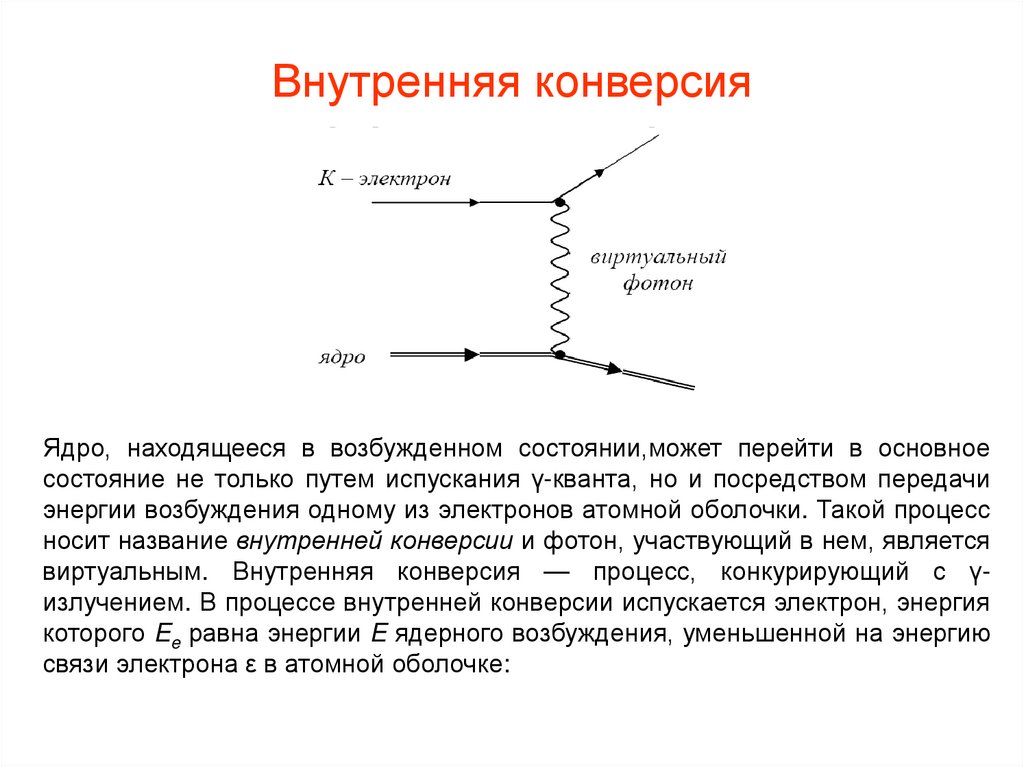
Внутренняя конверсия
Ядро, находящееся в возбужденном состоянии,может перейти в основное
состояние не только путем испускания γ-кванта, но и посредством передачи
энергии возбуждения одному из электронов атомной оболочки. Такой процесс
носит название внутренней конверсии и фотон, участвующий в нем, является
виртуальным. Внутренняя конверсия — процесс, конкурирующий с γизлучением. В процессе внутренней конверсии испускается электрон, энергия
которого Ee равна энергии E ядерного возбуждения, уменьшенной на энергию
связи электрона ε в атомной оболочке:

54.

Внутренняя конверсия
Моноэнергетичность вылетающих при внутренней конверсии электронов
позволяет отличить их от электронов β-распада, спектр которых непрерывен.
Помимо конверсионных электронов, при внутренней конверсии наблюдаются
еще и кванты рентгеновского излучения, возникающие при переходе одного
из наружных электронов на уровень K- или L-оболочки, освобожденный
вылетевшим из атома электроном.

55.

253
255
No
Lr 2.5 sec
50
8001
30 sec
0
8470
279
221
129
279
58
0
8280
8320
8370
160
8420
150
110
71 b
129 b 58
60
8530
0
249
Fm
251
Md

56.

Кластерная радиоактивность
В 1984 году был обнаружен радиоактивный распад 223Ra с вылетом ядер 14C.
Из экспериментов следовало, что вероятность испускания ядер 14C почти на 10
порядков меньше вероятности испускания α-частиц. Ядра 14C детектировались
ΔE − E телескопом полупроводниковых детекторов, что позволило надежно
отделить случаи многократных наложений α-частиц и дискриминировать ядра
14C по их заряду и массе. Решающим фактором, который привел к открытию
кластерной радиоактивности, был выбор распадающегося ядра. Выигрыш в
энергии распада для ядер близких к магическим приводит к наибольшей
проницаемости потенциального барьера и повышенной вероятности
испускания определенного кластера. Спонтанный вылет ядер 14C был вскоре
обнаружен и для ядер 221Fr, 221Ra, 222Ra. В настоящее время известно свыше10
изотопов, для которых обнаружена кластерная радиоактивность. Наряду с
испусканием ядер 14C наблюдалось испускание ядер 24Ne, 28Mg, 32Si.
Зависимость логарифма парциального
периода
кластерного
распада
от
логарифма проницаемости кулоновского
потенциального барьера.