Разработка программных модулей

1.

Разработка
программных модулей

2.

Оценка сложности алгоритма
Что такое алгоритм?
2

3.

Оценка сложности алгоритма
В широком смысле алгоритм — это последовательность действий, которые
нужно выполнить, чтобы получить определённый результат.
C научной точки зрения определение алгоритма, которое указано выше, не
совсем точное. Ведь не всякую последовательность действий, приводящую к
результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для
решения конкретного множества задач, который получает входные данные и
возвращает результат за конечное время.
3

4.

Оценка сложности алгоритма
Существуют различные алгоритмические последовательности. Какие?
4

5.

Оценка сложности алгоритма
Алгоритмические последовательности:
• Линейная
• Ветвления
• Циклическая
5

6.

Оценка сложности алгоритма
У алгоритмов есть два замечательных качества: они позволяют эффективно
решать задачи и не изобретать решения, которые кто-то уже придумал до
нас. Это справедливо как для повседневной жизни, так и для IT.
Кроме того, алгоритмы позволяют решать «нерешаемые» задачи, такие как
«задача коммивояжёра»
6

7.

Оценка сложности алгоритма
Можно выделить следующие свойства алгоритмов:
конечность,
определённость,
наличие ввода,
наличие вывода, или результативность,
универсальность,
эффективность.
7

8.

Оценка сложности алгоритма
Алгоритмы описывают с помощью двух характеристик — времени и памяти.
Время — это… время, которое нужно алгоритму для обработки данных.
Например, для маленького массива — 10 секунд, а для массива побольше —
100 секунд. Интуитивно понятно, что время выполнения алгоритма зависит
от размера массива.
Но есть проблема: секунды, минуты и часы — это не очень показательные
единицы измерения. Кроме того, время работы алгоритма зависит от
железа, на котором он выполняется, и других внешних факторов. Поэтому
время считают не в секундах и часах, а в количестве операций, которые
алгоритм совершит. Это надёжная и, главное, независимая от железа
метрика.
8

9.

Оценка сложности алгоритма
Когда говорят о Time Complexity или просто Time, то речь идёт именно о
количестве операций. Для простоты расчётов разница в скорости между
операциями обычно опускается. Поэтому, несмотря на то, что деление чисел
с плавающей точкой требует от процессора больше действий, чем сложение
целых чисел, обе операции в теории алгоритмов считаются равными по
сложности.
9

10.

Оценка сложности алгоритма
Существуют разные подходы к оценки сложности
10

11.

Оценка сложности алгоритма
Данные подходы называются асимптотический анализ. Это метод изучения
производительности алгоритмов при различных объемах и типах входных
данных.
Асимптотические нотации — это графики функций. Они служат для описания
времени работы алгоритма, когда размер входных данных стремится к
определенному значению или пределу.
В основном используются три нотации:
• большое «О»,
• омега-нотация,
• тета-нотация.
11

12.

Оценка сложности алгоритма
Большое «О» — это верхняя граница скорости выполнения алгоритма. Эта
нотация показывает скорость алгоритма в худшем случае.
Омега нотация — противоположность большому «О». Она показывает
нижнюю границу скорости выполнения алгоритма. Она описывает лучший
случай выполнения алгоритма.
Тета-нотация объединяет в себе сразу две функции — верхнюю и нижнюю.
Эта нотация отражает и верхнюю, и нижнюю границу скорости выполнения
алгоритма. Именно поэтому она используется для анализа средней скорости
выполнения алгоритма.
12

13.

Оценка сложности алгоритма
Память, или место, — это объём оперативной памяти, который потребуется
алгоритму для работы. Одна переменная — это одна ячейка памяти, а массив
с тысячей ячеек — тысяча ячеек памяти.
В теории алгоритмов все ячейки считаются равноценными. Например, int a
на 4 байта и double b на 8 байт имеют один вес. Потребление памяти обычно
называется Space Complexity или просто Space, редко — Memory.
13

14.

Оценка сложности алгоритма
Алгоритмы, которые используют исходный массив как рабочее пространство,
называют in-place. Они потребляют мало памяти и создают одиночные
переменные — без копий исходного массива и промежуточных структур
данных. Алгоритмы, требующие дополнительной памяти, называют out-ofplace. Прежде чем использовать алгоритм, надо понять, хватит ли на него
памяти, и если нет — поискать менее прожорливые альтернативы.
14

15.

Оценка сложности алгоритма
Идея оценки «в целом» пришла к нам из математики, где есть похожая
задача — нужно оценивать порядок роста функций. Математики могут точно
рассчитать скорость возрастания функции в любой точке, но эта информация
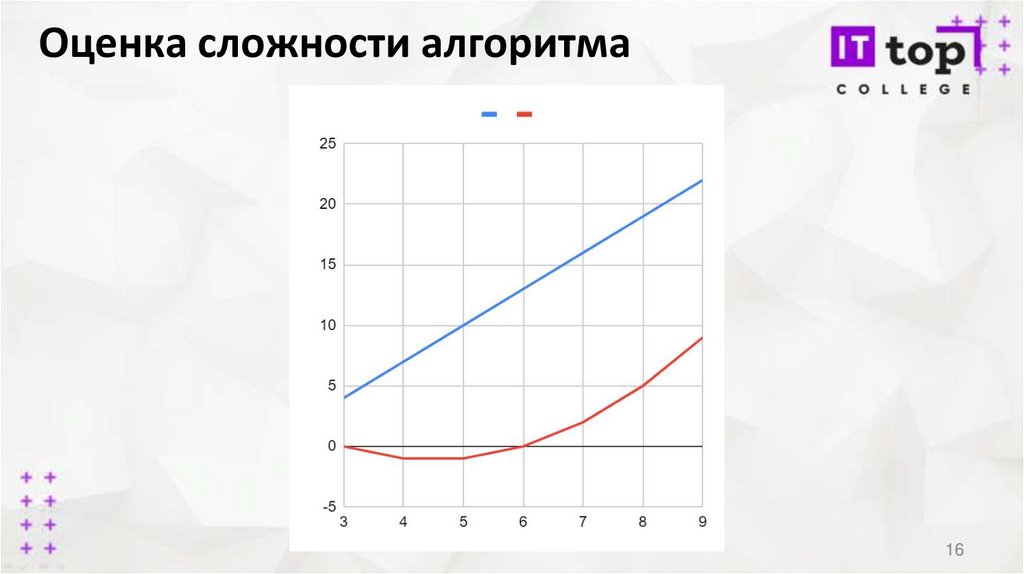
может оказаться не очень полезной. Сравним графики двух функций:
15

16.

Оценка сложности алгоритма
16

17.

Оценка сложности алгоритма
17

18.

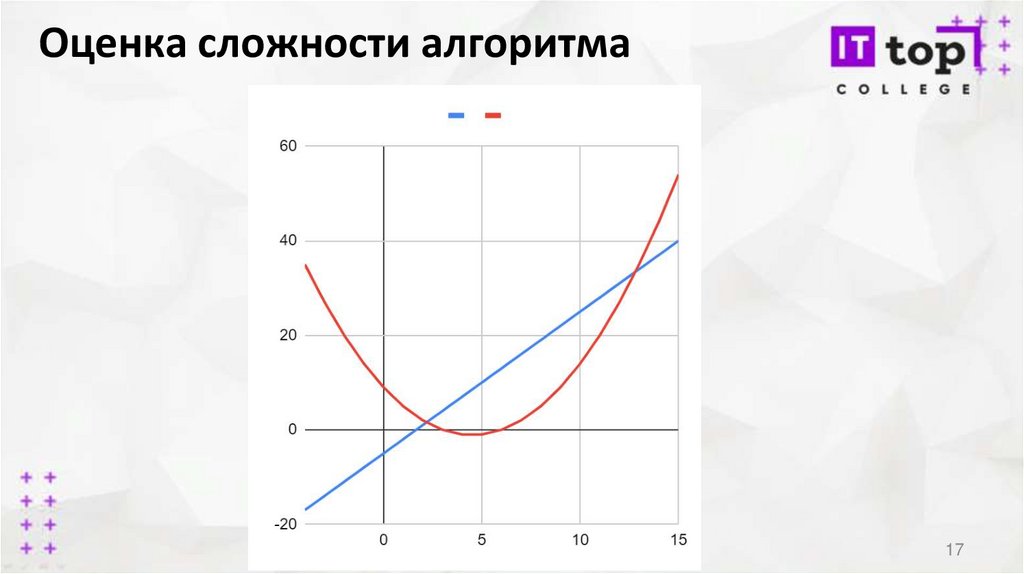
Оценка сложности алгоритма
Красная функция растет гораздо быстрее и почти сразу становится больше
синей. С алгоритмами возникает та же проблема: на одном наборе данных
первый алгоритм физически будет быстрее второго, на многих других
наборах он может оказаться гораздо медленнее. Синяя функция на графике
— это прямая линия, а красная — это парабола.
Синие функции в математике принято называть линейными, а красные —
квадратичными. Математики знают, что квадратичные функции растут
быстрее линейных, а кубические — быстрее квадратичных.
Алгоритмическая сложность тоже бывает линейной, квадратичной и
кубической. Для нее характерна та же самая зависимость: алгоритмы с
квадратичной сложностью в целом работают медленнее алгоритмов с
линейной сложностью.
18

19.

Оценка сложности алгоритма
Чтобы определить временную сложность алгоритма, программисты ставят
мысленный эксперимент. Предположим, что мы точно измерили время
работы алгоритма на одном массиве, а потом увеличили этот массив в десять
раз. Как увеличится время работы алгоритма? Если время работы алгоритма
также увеличится в десять раз, то речь идет о линейной сложности — на
графике она бы описывалась прямой линией.
19

20.

Оценка сложности алгоритма
Типичный линейный алгоритм — поиск минимального элемента в массиве:
const getMinimum = (items) => {
let minimum = items[0];
for (let i = 1; i < items.length; i++) {
if (minimum > items[i]) {
minimum = items[i];
}
}
return minimum;
};
20

21.

Оценка сложности алгоритма
Это простой алгоритм. Мы просматриваем элементы массива по одному и
сравниваем с уже найденным. Если новый элемент оказывается меньше
минимума, он становится новым минимумом. В самом начале в качестве
минимума выбираем самый первый элемент массива с индексом . Функция
состоит из двух смысловых элементов. Первый элемент — инициализация:
let minimum = items[0];
21

22.

Оценка сложности алгоритма
Второй элемент — это цикл:
for (let i = 1; i < items.length; i++) {
if (minimum > items[i]) {
minimum = items[i];
}
}
22

23.

Оценка сложности алгоритма
Если в массиве 10 элементов, цикл выполнится 9 раз, если 100 элементов —
99 раз, если n элементов, цикл выполнится n-1 раз. В итоге, для массива из n
элементов функция выполнит n операций — одну операцию инициализации
и n-1 операций в цикле. Если увеличить размер массива в 10 раз, то
количество элементов будет равно 10*n, и количество операций также будет
равно 10*n, то есть тоже вырастет в 10 раз.
Такая линейная временная сложность обозначается O(n). Из-за того, что в
записи используется большая буква O, она называется «нотация О-большое».
Буква появилась здесь не случайно. Это первая буква немецкого слова
Ordnung, которое означает порядок. В математике, откуда пришло
обозначение, оно относится к порядку роста функций.
23

24.

Оценка сложности алгоритма
Квадратичную сложность имеют, как правило, алгоритмы с двумя
вложенными циклами вида:
for (i = 0; i < items.length - 1; i++) {
for (j = i + 1; j < items.length; j++) {
// …
}
// …
}
24

25.

Оценка сложности алгоритма
Попробуем оценить количество выполнений цикла. На первом шаге
внешнего цикла внутренний выполнится n-1 раз, на втором n-2 раз, на
третьем n-3 и так далее.
25

26.

Оценка сложности алгоритма
Алгоритмическая сложность позволяет сравнивать алгоритмы «в целом».
Можно утверждать, что все линейные алгоритмы в целом быстрее всех
квадратичных, хотя на конкретных данных возможны аномалии. Все
квадратичные алгоритмы в целом быстрее всех кубических.
К сожалению, сравнивая два линейных алгоритма, мы не можем сказать,
какой из них быстрее.
26

27.

Оценка сложности алгоритма
Определяя алгоритмическую сложность, мы считаем количество операций и
предполагаем, что все они выполняются за небольшое постоянное время.
Но как только речь заходит о конкретике, выясняется, что операция сложения
может быть очень быстрой, а операция деления — очень медленной по
сравнению со сложением. Иногда четыре сложения могут выполниться
быстрее, чем два деления.
в О-нотации на операции с одной или двумя переменными вроде i++, a * b, a
/ 1024, max(a,b) уходит всего одна единица времени.
27

28.

Оценка сложности алгоритма
Рассмотрим более интересный алгоритм – определитель палиндромов.
const palindrome = (string) => {
for (let i = 0; i < string.length / 2; i++) {
if (string[i] != string[string.length - 1 - i]) {
return false;
}
}
return true;
};
palindrome('') // true
palindrome('a') // true
28

29.

Задание
Сколько раз выполнится цикл в определителе палиндромов, если длина строки, приходящей на
вход = n?
Сколько операций на выполнение алгоритма потребуется в целом?
const palindrome = (string) => {
for (let i = 0; i < string.length / 2; i++) {
if (string[i] != string[string.length - 1 - i]) {
return false;
}
}
return true;
};
palindrome('') // true
palindrome('a') // true
palindrome('ab') // false
palindrome('aha') // true
palindrome('abba') // true
29

30.

Домашнее задание
Оцените кол-во операций, требуемых для выполнения данного алгоритма с длиной входящей
строки n?
int FindSpace(string s)
{
int i = 0;
while (i < s.Length && s[i] != ' ')
i++;
return i >= s.Length ? -1 : i;
}

31.

Спасибо за внимание!