Функция Эйлера и ее формула

1. Функция Эйлера и ее формула

ВЫПОЛНИЛ СТУДЕНТ ИСИТ 1 КУРСА
БАБКИН ВАЛЕНТИН

2. Введение

Функция Эйлера, обозначаемая как φ(n),
является фундаментальной в теории чисел.
Она определяет количество положительных
целых чисел, меньших n, которые взаимно
просты с n.

3. Определение

Функция Эйлера φ(n) определяется как
количество натуральных чисел, не
превосходящих n и взаимно простых с n.
Пояснение: взаимно простыми называются
числа, которые не имеют общих делителей,
отличных от 1. Так как делителями нуля
являются все натуральные числа, то 0
взаимно прост только с 1.

4. Формула функции Эйлера

5. Пример вычисления

Пример:
• Рассмотрим n=9:
• Числа: 1, 2, 3, 4, 5, 6, 7, 8
• Взаимно простые: 1, 2, 4, 5, 7, 8.
• φ(9)=6.

6. Общие сведения

Функция Эйлера φ(n) показывает, сколько
натуральных чисел из отрезка [1, n – 1]
имеют c n только один общий делитель —
единицу.
Функция Эйлера определена на множестве
натуральных чисел, и значения её лежат во
множестве натуральных чисел.

7. Свойства функции Эйлера

Мультипликативность: если m и n взаимно
просты, то φ(mn)=φ(m)⋅φ(n).
Функция Эйлера от простого
числа: φ(p)=p−1

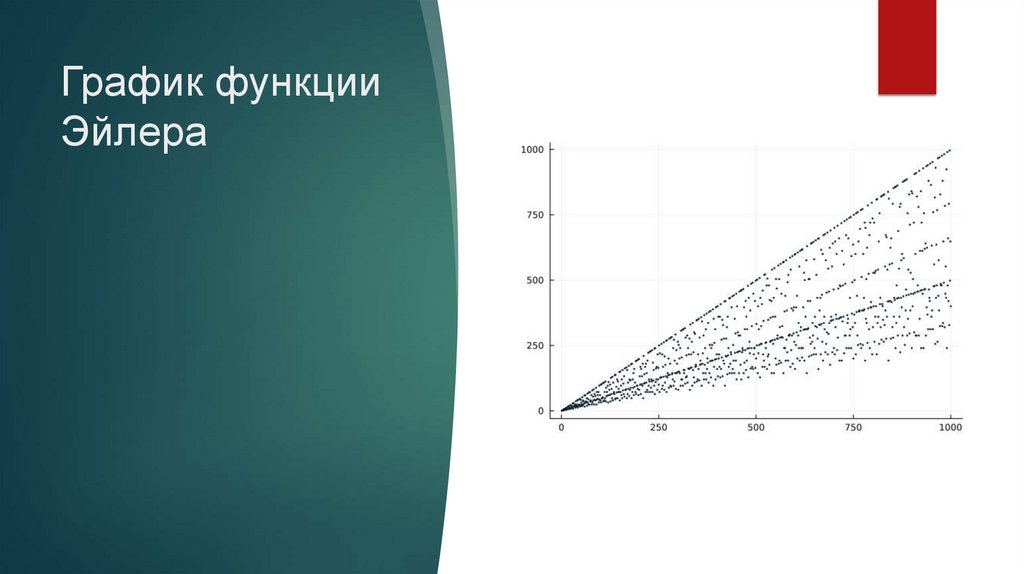
8. График функции Эйлера

9. Применение функции

Криптография: Используется в системе RSA
для генерации ключей.
Теория чисел: Исследование свойств чисел
и их делимости.

10. Связь с другими областями

• Комбинаторика: Функция Эйлера играет
роль в задачах на перестановку и выбор,
позволяя подсчитывать количество
определенных комбинаций.
• Компьютерные науки: Функция Эйлера
используется в различных алгоритмах
для вычисления зависимостей в
программировании и шифровании.

11. Заключение

Функция Эйлера — краеугольные камнень
не только теории чисел, но и множества
прикладных вычислений, которые важны в
современном мире.

12. Литература

Виноградов И. М. "Основы теории чисел".
Арнольд В. И. "Группы Эйлера и
арифметика геометрических прогрессий".
Арнольд В. И. "Введение в современные
методы математики".