Хеширование

1. хеширование

• хеширование - это необычный метод
поиска в необычном массиве
• Гулаков В. К. Введение в
хеширование: монография – Брянск:
БГТУ, 2011. – 129 с.
1

2. Основные понятия хеширования

С хешированием мы сталкиваемся едва ли не на
каждом шагу:
–при работе с браузером (список Web-ссылок),
– текстовым редактором и переводчиком (словарь),
–языками скриптов (Perl, Python, PHP и др.),
– компилятором (таблица символов).
По словам Брайана Кернигана, это «одно из
величайших изобретений информатики».
Например, упорядочение по алфавиту является
не чем иным, как хешированием.
2

3.

• До сих пор мы рассматривали методы поиска,
основанные на сравнении данного аргумента K с
имеющимися в таблице ключами или на
использовании его цифр для управления
процессом разветвления.
• Эффективность поиска зависит от структуры
данных.
– В случае последовательной структуры данных
гарантированно просматривается O(n) элементов,
– в случае бинарных поисковых деревьев и при
бинарном поиске обеспечивается более высокая
эффективность O(log2n),
• т.е. сложность алгоритма поиска зависит от
размера таблицы.
3

4.

• В идеале нам хотелось бы выбирать
данные за время O(1), когда число
необходимых сравнений не зависит
от количества элементов данных.
• Например, выборка элемента
осуществляется за время O(1) при
использовании в качестве индекса в
массиве некоторого ключа.
4

5.

• Эффективность поиска можно
повысить, если вместо различных
упорядоченных структур использовать
так называемые беспорядочные или
перемешанные структуры данных.
• Mожно произвести над ключом K
некоторое арифметическое вычисление
с помощью функции f(K), указывающую
адрес в таблице, где хранится ключ K и
ассоциированная с ним информация.
5

6.

• Основная идея ассоциативной
адресации состоит в том, чтобы
рассматривать адрес как
функцию от ключа.
• Требуется, чтобы этот адрес
вычислялся как можно проще и
как можно быстрее.
6

7.

• Хеширование полезно, когда широкий
диапазон возможных значений ключа
должен быть сохранен в малом объеме
памяти, и нужен способ быстрого
доступа.
• Хэш-таблицы часто применяются в
базах данных, и, особенно, в языковых
процессорах типа компиляторов и
ассемблеров, где они изящно
обслуживают таблицы
идентификаторов. В таких приложениях
хеш-таблица - наилучшая структура
данных.
7

8.

• Пример 1. Файл клиентов пункта проката
содержит шестизначные номера телефонов.
Номер телефона используется в качестве
ключа для доступа к конкретной записи
файла клиентов, но вряд ли пункт проката
хранит миллионный массив.
• Если имеется не более 1000 клиентов, то
можно использовать массив примерно такой
же длины. Тогда целесообразно
преобразовать номера телефонов в
трехзначные числа и использовать их в
качестве адреса (индекса).
8

9.

• хеш-таблица - это обычный одномерный
массив с необычной адресацией,
задаваемой хеш-функцией.
• Размер хеш-таблицы m должен быть
достаточно большим, чтобы в ней
оставалось разумно большое число
пустых мест.
• Если число записей n невелико и заранее
известно, то можно построить идеальную
хеш-функцию. Это называется идеальным
или совершенным хешированием
• Если же число записей велико, то найти
такую функцию очень сложно.
9

10.

• В случае, когда в результате хеширования
ключи претендуют на один и тот же адрес
приходится отказываться от идеи
однозначности..
• Отказ от требования взаимно однозначного
соответствия между ключом и адресом
означает, что для двух различных ключей k1
k2 значение хеш-функции может
совпадать: h(k1) = h(k2). Такая ситуация
называется коллизией.
10

11.

• Для метода хеширования главными
задачами являются:
– выбор хеш-функции h так, чтобы уменьшить
число коллизий;
– нахождение способа разрешения
возникающих коллизий, т.е. где разместить
конфликтные записи - внутри самого массива
или вне его.
• Мерой использования памяти в таблицах с
прямым доступом служит коэффициент
заполненности, определяемый как
отношение числа записей к числу мест в
11
таблице α = n/m.

12.

Методы хеширования являются самыми
быстрыми из известных методов поиска,
но имеют три недостатка.
1. табличный порядок имен обычно не связан с
их естественным порядком.
2. худший случай может оказаться хуже, чем
при последовательном поиске.
3. таблицы, основанные на вычислении адреса,
расширить динамически непросто: это может
приводить к потере памяти, если таблица
слишком
велика,
или
к
малой
производительности, если таблица слишком
мала.
12

13.

• Хеширование не является панацеей по
двум основным причинам:
– Во-первых, время выполнения зависит от
длины ключа, которая может быть
значительной в реальных приложениях,
использующих длинные ключи.
– Во-вторых, хеширование не обеспечивает
эффективные реализации для других
операций, таких как select или sort, с
таблицами символов.
• Один из наиболее эффективных способов
реализации словаря - хеш-таблица.
13

14.

• Вне зависимости от используемого
метода хеширования сама процедура
занесения элемента делится на три
этапа:
–вычисление хеш-адреса
(по хеш-функции);
–уточнение хеш-адреса
(в случае коллизии);
–размещение ключа
(и/или элемента).
14

15.

• Пример Рассмотрим таблицу, в которой ключевое поле имеет
следующие семь ключей:
• 54, 77, 94, 89, 14, 45, 76
• Очевидно, что использование этих ключей в качестве индекса не
эффективно. Наиболее разумно использовать здесь хеширование.
Размер хешируемой таблицы А определим из соображений
заполнения таблицы более чем на 50% и он был бы взаимно
простым числом, например 11. Для хеширования используем
простейшую хеш-функцию h(key)=mod(key,11).
• Хеширование первых пяти ключей дает пять различных индексов,
т.е. не вызывает коллизий
0 1 2 3 4 5 6 7 8 9 10
• А [77 89
14
94
54]
45
76
• Для того чтобы поместить ключ 76 на свободное место, надо
сделать 5 попыток последовательного просмотра ячеек. Общее
число проб для размещения в таблице всех элементов списка равно
13, т.е. в среднем 1,9 проб на элемент.
• В общем случае функция повторного хеширования rh
воспринимает один индекс в массиве и выдает другой индекс.
15

16. Хеш-функции Требования к хеш-функциям

Имеется много разных хеш - функций, каждая со
своими преимуществами и недостатками в
зависимости от набора хешируемых ключей.
Требования при выборе хеш-функции:
- минимальная сложность ее вычисления;
- равномерность распределения значений хеш-функции
по хеш-таблице, что позволяет:
сократить число коллизий;
не допустить скучивания значений ключей в отдельных частях
таблицы.
Если ключи не являются числами, то они должны быть
преобразованы в целые числа перед применением
хеш-функций.
Хеш-функция не может вычислять адреса больше чем
размер хеш-таблицы, причем для всех ключей К
0 < h(K) < m, где m – размер хеш-таблицы.
16

17. Классы хеш-функций

• Различают три класса хеш-функций:
• Идеальные
• Универсальные
• Специальные
• Для каждого конкретного множества
возможных ключей можно подобрать свою,
возможно наилучшую, хеш-функцию
распределения ключей по таблице.
17

18. Как выбрать класс хеш-функций ?

• Если содержание таблицы строго определено,
число хешируемых ключей невелико, то можно
найти идеальную хеш-функцию, но любой новый
ключ может ухудшить эту функцию.
• Класс универсальных хеш-функций используется в
большинстве случаев, если они позволяют
равномерно распределять ключи по хеш-таблице.
• Если трудно подобрать эффективную
универсальную хеш-функцию, то применяются
специальные хеш-функции, зависящие от
распределения ключей
18

19. Идеальные хеш – функции

• Идеальной (perfect hash function) или
«минимальной совершенной» хеш-функцией
называется такая хеш функция, когда:
– не возникает коллизий;
– размер хеш таблицы и количество ключей одинаково
• Это идеальный случай с точки зрения
потребления памяти и скорости работы.
Однако, поиск таких функций – очень
нетривиальная задача.
19

20. Совершенное хеширование

• Совершенное хеширование – это
когда нет коллизий, но размер хештаблицы несколько больше
количества хешируемых ключей

21. Основные алгоритмы поиска идеальных хеш-функций

– Метод проб и ошибок, предложенный Дж.
Чикелли
– Метод обратных чисел, разработанный Дж.
Джеске
– Алгоритм, основанный на случайных
графах, рассмотренный С. Ботело
21

22.

Метод проб и ошибок
• Согласно этому методу, h вычисляется как
сумма кодов букв ключа. Обозначим через Сj
код, соответствующий j-й букве ключа k, Тогда
можно записать
l
h(k ) (( C j ( L j )) mod m).
j 1
• Значения C(L) для различных L не обязательно
должны быть различными, т. е. хотя все буквы
множества L1 ..., Ll различны, среди
соответствующих им кодов С1, С2, .., Сl могут
быть и одинаковые.
22

23.

Алгоритм
• Вначале упорядочиваем буквы по частоте их
использования в словах и присваиваем им коды
0,1,2, ... начиная с буквы, обладающей большей
частотностью.
• Затем вычисляем значения хеш-функции для
каждого ключа, используя числовые коды букв, и
упорядочиваем ключи по значениям h(k).
• В случае коллизий исследуем, не может ли
функция стать минимально совершенной, если
изменить коды букв, обладающих малой
частотностью.
• Для слов, содержащих буквы с частотностью 1,
за счет изменения кодов этих букв удается
довольно свободно изменять h(k). Корректируя
коды букв невысокой частотности, можно
довольно успешно избежать коллизий.
23

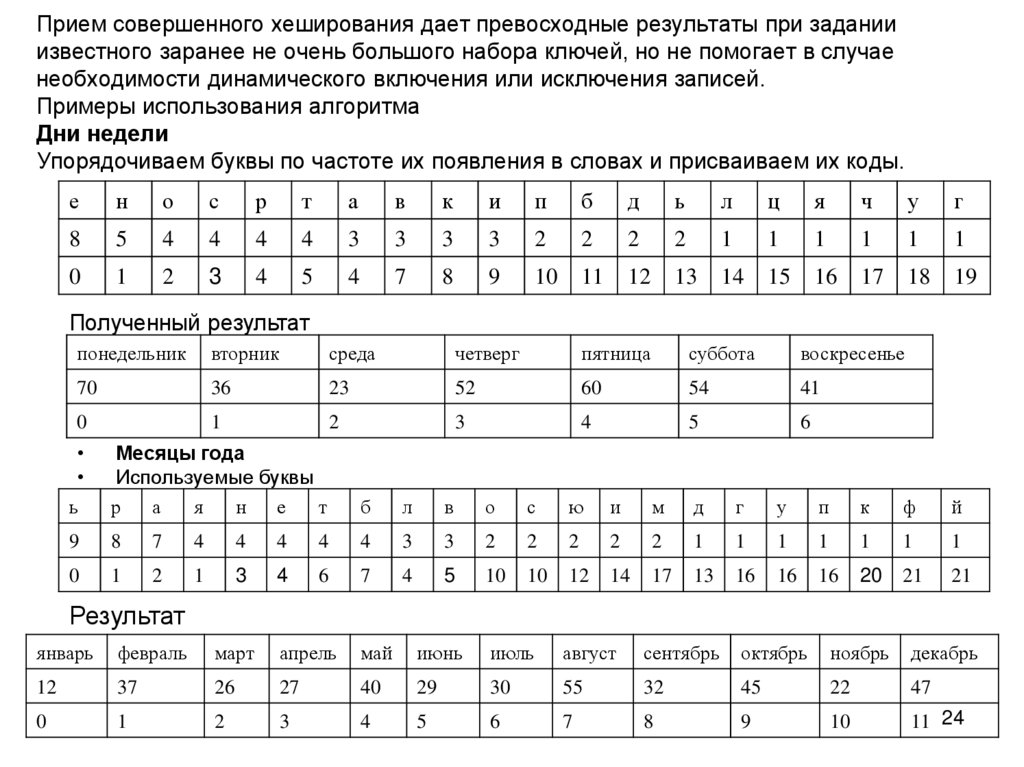
24. Прием совершенного хеширования дает превосходные результаты при задании известного заранее не очень большого набора ключей, но

не помогает в случае
необходимости динамического включения или исключения записей.
Примеры использования алгоритма
Дни недели
Упорядочиваем буквы по частоте их появления в словах и присваиваем их коды.
е
н
о
с
р
т
а
в
к
и
п
б
д
ь
л
ц
я
ч
у
г
8
5
4
4
4
4
3
3
3
3
2
2
2
2
1
1
1
1
1
1
0
1
2
3
4
5
4
7
8
9
10
11
12
13
14
15
16
17
18
19
Полученный результат
понедельник
вторник
среда
четверг
пятница
суббота
воскресенье
70
36
23
52
60
54
41
0
1
2
3
4
5
6
ь
Месяцы года
Используемые буквы
р
а
я
н
е
т
б
л
в
о
с
ю
и
м
д
г
у
п
к
ф
й
9
8
7
4
4
4
4
4
3
3
2
2
2
2
2
1
1
1
1
1
1
1
0
1
2
1
3
4
6
7
4
5
10
10
12
14
17
13
16
16
16
20
21
21
Результат
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь
12
37
26
27
40
29
30
55
32
45
22
47
0
1
2
3
4
5
6
7
8
9
10
11 24

25. Разновидности универсальных хеш – функций

• При хешировании для вычисления адреса
используются много различных функций, каждая
из которых имеет свои преимущества и
недостатки. Наиболее известные хеш-функции:
– метод деления;
– метод умножения;
– метод "середины квадрата";
– метод свертки (слияния);
– метод преобразования системы счисления;
– метод деления многочленов;
– хеш-функция для строковых ключей,
– и другие.
25

26. метод деления

• На практике метод используется в
большинстве приложений, работающих
с хешированием и требует двух шагов:
– в начале ключ должен быть преобразован
в целое число;
– затем полученное значение вписывается в
диапазон 0...m-1 (m-размер хеш-таблицы) с
помощью оператора получения остатка.
• H=mod(k, m),
где k- ключ, m-размер хеш-таблицы.
26

27.

• Пример 1: ключ k– пятизначное число. Хешфункция извлекает две младшие цифры.
• Например, если это число равно 56389, то
H(56389) = 89. Две младшие цифры являются
остатком от деления на 100.
– int H (int key)
–{
– return key % 100; // метод деления на 100
–}
• Эффективность хеш-функции зависит от того,
обеспечивает ли она равномерное
распределение ключей в диапазоне 0...m-1.
• Если две последние цифры соответствуют году рождения, то будет
слишком много коллизий при идентификации подростков.
27

28.

• Пример 2 – ключ-символьная строка С++.
Хеш-функция отображает эту строку в
целое число посредством суммирования
первого и последнего символов и
последующего вычисления остатка от
деления на 101 (размер таблицы).
• Эта хеш-функция приводит к коллизии при
одинаковых первом и последнем
символах строки. Например, строки «start»
и «slant» будут отображаться в индекс 29.
• Так же ведет себя хеш-функция,
суммирующая все символы строки.
28

29. Метод умножения (мультипликативный)

• Для мультипликативного хеширования используется
следующая формула:
• h(K) = m * ((C * K) mod 1)
• Здесь производится умножение неотрицательного
целого ключа на некую константу С, лежащую в
интервале [0..1]. После этого берется дробная часть
этого выражения и умножается на некоторую
константу m (размер хеш-таблицы), выбранную
таким образом, чтобы результат не вышел за
границы хеш-таблицы. Оператор возвращает
наибольшее целое, которое меньше аргумента.
29

30.

• Если константа С выбрана верно, то можно
добиться очень хороших результатов, однако,
этот выбор сложно сделать.
• Частным случаем выбора константы C является
значение золотого сечения
– φ = (√5 - 1)/2 ≈ 0,6180339887.
• Если взять последовательность {φ}, {2φ}, {3φ},...
где оператор { } возвращает дробную часть
аргумента, то на отрезке [0..1] она будет
распределена очень равномерно.
• В доказательстве играют важную роль числа
Фибоначчи. Такое хеширование называется
хешированием Фибоначчи.
30

31. Метод "середины квадрата"

Метод "середины квадрата"
• Метод предусматривает преобразование
ключа в целое число, возведение его в
квадрат и возвращение в качестве
значения функции хеширования m битов,
извлеченных из середины полученного
числа.
• Практически адрес получается отсечением
битов или цифр от обоих концов
произведения, которое выполняется до тех
пор, пока число оставшихся битов или
цифр не станет равным требуемой длине
адреса.
31

32. Анализ метода "середины квадрата"

Анализ метода "середины квадрата"
• Причиной возведения числа в квадрат до
извлечения средних цифр является то, что все
цифры первоначального числа дают свой
вклад в значение средних цифр квадрата.)
• Метод середины квадрата подвергался критике,
но его применение к некоторым наборам ключей
дает хорошие результаты.
• Эксперименты с реальными данными
показывают, что метод "середины квадрата"
неплох при условии, что ключи не имеют
большого количества нулей слева или справа, но
по многим параметрам он уступает методу
умножения.
32

33. Метод свертки (слияния)

• В методе свертывания ключ разбивается на
части, каждая из которых имеет длину,
равную длине требуемого адреса (кроме,
возможно, последней части).
• Чтобы сформировать адрес, части
складываются, при этом игнорируется
перенос в старшем разряде. Если ключи
представлены в двоичном виде, то вместо
сложения может быть использована
операция исключающего ИЛИ.
• Существуют различные, вариации этого
метода,
33

34.

• Метод проиллюстрируем на конкретном
примере ключа 187249653. В методе
свертывания со сдвигом складываются числа
187, 249 и 653, при этом получается адрес 89.
• В методе граничного свертывания
инвертируются цифры в крайних частях ключа, и
таким образом в нашем примере складываются
числа 781, 249 и 356, что дает адрес 386.
• Свертывание является функцией хеширования,
удобной для сжатия многословных ключей и
последующего перехода к другим функциям
хеширования. Естественно, могут быть
предложены другие способы разбивки на части.
34

35. Специальные хеш – функции

• Все рассмотренные до сих пор функции хеширования не
зависят от закона распределения значений ключей.
• Функции хеширования, зависящие от закона
распределения ключей, отличны от универсальных.
• Тогда для заданного ключа х зависящая от
распределения ключей функция хеширования Н,
определяется выражением
– Н (х) = mF(x) .
• Однако в большинстве случаев функция распределения F
неизвестна и должна быть аппроксимирована. Все
зависящие от закона распределения ключей функции
хеширования различаются лишь подходом, используемым
для оценки F.
35

36.

• Известны различные подходы к формированию
специальных хеш функций:
– Хеш-преобразование, известное под названием
поразрядного анализа, в определенной степени
является, зависящим от распределения. Адреса
формируются путем выбора и сдвига цифр или битов
исходного ключа.
– Другой зависящей от распределения функцией,
хеширования, которую можно использовать для
аппроксимации F, является кусочно-линейная
функция. Пространство ключей, состоящее из целых
величин в замкнутом интервале [a, d], делится на j
равных подинтервалов длины L
– Вычисление кусочно-линейной функции для
непрямой адресации обеспечивается алгоритмом
36
изложенным у Трамбле.

37. Оценка качества хеш-функции

• Для того чтобы предварительно оценить качество
хеш-функции можно провести имитационное
моделирование.
• Моделирование проводится следующим образом.
Формируется целочисленный массив, длина которого
совпадает с длиной хеш-таблицы. Случайно
генерируется достаточно большое число ключей, для
каждого ключа вычисляется хеш-функция. В
элементах массива просчитывается число генераций
данного адреса. По результатам такого
моделирования можно построить график
распределения значений хеш-функции.
37

38.

38

39. Коллизии и пути их преодоления

• Традиционно рассматриваются две
классические стратегии разрешения коллизий:
открытую адресацию с линейным
перебором
метод цепочек.
Возможны различные варианты этих стратегий,
которые имеют свои достоинства и недостатки.
39

40. методы открытой адресации

• Суть методов - пользуясь какимлибо правилом, обеспечивающим
перебор всех элементов, просто
просматривать один за другим
элементы хеш-таблицы.
• Метод аналогичен процедуре, когда на
письмо к человеку, постоянно
перемещающемуся с места на место, делают
наклейки с новыми адресами, по которым
письмо пересылается вслед за адресатом.
40

41.

Алгоритм открытой адресации в общем виде можно
описать следующим образом:
1. Вычисляем адрес точки входа в таблицу а = h(k)по ключу k.
Установим i = 0.
2. Если ячейка Т[а] свободна, то записи с ключом k в таблице нет.
При вставке в строку помещаются запись и удачный конец
алгоритма; при поиске — конец алгоритма при отсутствии ключа.
3. Если ключ в строке Т[а] равен k, тогда при вставке — конец
алгоритма по признаку «дублирующий ключ», при поиске —
удачный конец и возврат адреса строки ai.
4. В противном случае — коллизия. Увеличиваем счетчик на 1: i =
(i + 1) и по некоторой функции вычисляем адрес ячейки внутри
таблицы ai = r(h(k), i). Переход на п. 2.
Функции r(h(k),i), 1≤i≤N, определяют
последовательность адресов для просмотра элементов
таблицы. Их выбор вызывает некоторые трудности и в
основном определяется особенностями использования
таблицы при решении конкретной задачи.
41

42.

Наиболее распространенными
схемами открытой адресации
являются:
– линейная открытая адресация (линейное
опробование);
– случайное опробование;
– квадратичная открытая адресация
(квадратичное опробование);
– открытая адресация с двойным
хешированием.
42

43. Линейное опробование

• каждая ячейка таблицы помечена как незанятая.
Поэтому при добавлении нового ключа всегда
можно определить, занята ли данная ячейка
таблицы или нет. Если да, алгоритм
осуществляет перебор по кругу, пока не
встретится «открытый адрес» (свободное место).
• Если размер таблицы велик относительно числа
хранимых там ключей, метод работает хорошо,
поскольку хеш-функция будет равномерно
распределять ключи по всему диапазону и число
коллизий будет минимальным.
• По мере того как коэффициент заполнения
таблицы приближается к 1, эффективность
процесса заметно падает.
43

44.

пример
• Предположим, что данные хранятся в 11элементной таблице.
• В качестве хеш-функции HF используется
остаток от деления на 11, принимающий
значения в диапазоне 0-10.
• HF(item) = item.key % 11
• В таблице хранятся следующие данные.
• Список: {54}, {77}, {94}, {89}, {14}, {45}, {76}
• В данном методе hi(k) = (h0(k) + сi) mod m, где
с — константа, т -размер хеш-таблицы. В
простейшем случае с равно 1 или -1.
• Общее число проб для размещения в таблице
всех элементов списка равно 13, т.е. в среднем
1,9 проб на элемент.
44

45. Случайное опробование.

• Недостаток метода линейного опробования обусловлен
эффектом скучивания, который значительно усиливается
при почти заполненной таблице.
• Проблема первичных скучиваний может быть частично
решена, если использовать другой метод опробования, а
именно, метод случайного опробования.
• При использовании этого метода генерируется
случайная последовательность позиций в отличие от
упорядоченной последовательности, справедливой для
метода линейного опробования. Генерируемая
случайная последовательность должна содержать все
целые числа от 1 до m в точности по одному разу.
Таблица считается заполненной, если встречается
первое дублирование случайного числа.
45

46.

• Примером генератора случайных чисел,
создающего такую циклическую
последовательность чисел, является оператор
• y ← (y + с) mod m;
• здесь у в скобках является предыдущим числом
последовательности, а с и m — взаимно
простые числа, т. е. их наибольший общий
делитель равен 1. Например, предположим, что
m = 11 и с = 7; тогда это выражение, начиная со
значения 3, генерирует следующую
последовательность чисел:
• 10, 6, 2, 9, 5, 1, 8, 4, 0, 7 и 3.
• Прибавление 1 к каждому элементу преобразует
полученную последовательность к требуемому
интервалу [1, 11].
• Теперь можно сформулировать следующий
46
алгоритм.

47. Алгоритм случайного опробывания

Дана запись REC, идентифицируемая ключом х;
требуется вставить ее в таблицу, представленную
структурой R. Для вычисления начального адреса
используется функция хеширования Н. Величина
MARK служит для пометки удаленной записи.
1.
2.
3.
4.
[Инициализация.] Установить d ← Н (х).
[Первая проба.] Если Кd < 0 или Kd = MARK, то установить Кd
← х и завершить выполнение алгоритма.
[Продолжение поиска]. Установить у ← d — 1.
[Сканирование следующей записи.]
Установить у ← (у + с) mod m и j ← у + 1; Если j = d, то печатать
'ПЕРЕПОЛНЕНИЕ' и завершить выполнение алгоритма.
5.
[Данная позиция таблицы занята?] Если Кj < 0 или Kj = MARK,
то установить Kj ← x и завершить выполнение алгоритма; в
противном случае перейти к шагу 4.
47

48.

• Для метода случайного опробования
проблема удаления записей становится
более сложной, чем в случае линейного
опробования. Поэтому в случае часто
меняющейся таблицы для устранения
коллизий следует использовать другие
методы.
• Произвольная адресация использует
заранее сгенерированный список
случайных чисел для получения
последовательности. Это дает выигрыш в
скорости, но несколько усложняет задачу
программиста.
48

49. Квадратичное опробование

• Это схема открытой адресации, при которой
hi(k)=h0(k)+ci+di2, где с и d — константы. Благодаря
нелинейности этой адресации удается избежать
увеличения числа проб при числе коллизий более
2. Однако в случае почти заполненной таблицы не
удается избежать «вторичного скучивания».
• Это связано с тем, что при большом числе ключей
коллизии одной группы вступают в коллизию с
другими ключами.
• Из примера, рассмотренного ранее, видно, что в
случае линейного опробования возникает 10
коллизий, а в случае квадратичного 5.
• С одной стороны, этот метод дает хорошее
распределение по таблице, а с другой занимает
больше времени для просчета.
49

50. Двойное хеширование

• Один из способов преодоления вторичного скучивания
состоит в использовании второй функции хеширования, не
зависящей от первой.
• Предположим, например, что первой функцией
хеширования является h1, такая, что h1(x1) = h1(х2) = i, где x1
≠ х2. Теперь, если мы имеем вторую функцию хеширования
h2 такую, что h2(x1) ≠ h2(х2) при x1≠ х2, то в качестве
значения параметра с можно использовать значение h2(х1)
или h2(х2). Если h1 и h2 являются независимыми, две
случайные последовательности адресов, сгенерированные
с помощью такого метода, будут различными.
Следовательно, мы избавляемся от вторичного скучивания.
Такая вариация метода открытой адресации называется
двойным хешированием.
50

51. метод цепочек

• Хеш-таблица рассматривается как массив связанных
списков или деревьев. Каждый такой список называется
блоком (bucket) и содержит записи, отображаемые хешфункцией в один и тот же табличный адрес. Эта
стратегия разрешения коллизий называется методом
цепочек (chaining with separate lists).
• Если таблица является массивом связанных списков, то
элемент данных просто вставляется в соответствующий
список в качестве нового узла. Чтобы обнаружить
элемент данных, нужно применить хеш-функцию для
определения нужного связанного списка и выполнить
там последовательный поиск.
51

52.

Пример
Список: {54,1}, {77,3}, {94,5}, {89,7}, {14,8}, {45,2}, {76,9}
HF(item) = item.key % 11
Каждый новый элемент данных вставляется в хвост соответствующего
связанного списка. На рисунке каждое значение данных сопровождается (в
скобках) числом проб, требуемых для запоминания этого значения в
таблице.
52

53.

• В общем случае метод цепочек быстрее
открытой адресации, так как просматривает
только те ключи, которые попадают в один и тот
же табличный адрес.
• Кроме того, открытая адресация предполагает
наличие таблицы фиксированного размера, в то
время как в методе цепочек элементы таблицы
создаются динамически, а длина списка
ограничена лишь количеством памяти.
• Списки образуются по мере необходимости по
одному на каждый возможный хеш-адрес
таблицы.
• Сами списки могут размещаться как в памяти,
принадлежащей хеш-таблице, так и в
отдельной памяти. В первом случае цепочки
называются внутренними, а во втором
случае — внешними.
53

54. Поиск в хеш таблице

Рядом с адресом в дополнительном поле записывается
информация о коллизии.
• Пример
– Последовательность содержит следующие данные:
– 54, 77, 94, 89, 14, 45, 76
– Размер хешируемой таблицы А равен 11. Для хеширования
используем простейшую хеш-функцию h(key)=mod(key,11). Для
преодоления коллизии используется линейное опробование
– Получаем следующую хеш таблицу
–
0 ,1 1,1 2,1 3,1 4,0 5,0
6,0
7,0 8,0 9,0 10,1
– А [77 89 45 14 76
94
54]
– Для того чтобы найти ключ 76, надо сделать 5 попыток
последовательного просмотра ячеек.
• при поиске хешированием переход от адреса к адресу
осуществляется по признаку коллизии
• При поиске с использованием метода цепочек
информация о коллизиях не требуется, а просто
54
пробегается соответствующая цепочка

55. Удаление элементов хеш-таблицы

• Обрабатывать удаление можно, помечая
элемент как удаленный, а не как пустой.
• Таким образом, каждая ячейка в таблице
будет содержать уже одно из трех
значений: пустая, занятая, удаленная.
• При поиске удаленные элементы будут
трактоваться как занятые, а при вставке –
как пустые, соответственно.
55

56. Другие методы хеширования

Линейное хеширование (linear hashing, LH)
Линейное хеширование с частичной экспансией(Larson, 1982).
Виртуальное хеширование ((virtual hashing, VH, Litwin, 1978),
Динамическое хеширование (dynamic hashing, DH)
Расширяемое хеширование (extendible hashing)
Trie хеширование. При использовании этого подхода индекс не
содержит всех символов ключа, а только его часть.
• Спиральное хеширование (Martin, 1979).
• Многомерное хеширование
MOLHPE - линейное хеширование при многомерном поиске
– - Z-Hashing
– - Quantile Hashing
Разновидности расширяемого хеширования при многомерном поиске
– - EXCELL
– – Grid File (R-File, Twin Grid File, BANG File)
• Хеширование по сигнатуре.
• Одностороннее хеширование
56