Исследование функции с помощью производной и построение ее графика

1. Исследование функции с помощью производной и построение ее графика

ИССЛЕДОВАНИЕ
ФУНКЦИИ С ПОМОЩЬЮ
ПРОИЗВОДНОЙ И
ПОСТРОЕНИЕ ЕЕ
ГРАФИКА

2. Общая схема исследования

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ
1) Найти область определения функции;
2) Найти точки пересечения графика с осями координат;
3) Найти интервалы знакопостоянства функции;
4) Найти промежутки монотонности функции и её
экстремумы;
5) Найти промежутки выпуклости графика функции и точки
перегиба;
6) Заполнить таблицу дополнительных значений;
7) Построить график функции, используя полученные
результаты исследования.

3. Задание: Исследовать функцию с помощью производной и построить её график

ЗАДАНИЕ: ИССЛЕДОВАТЬ ФУНКЦИЮ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
И ПОСТРОИТЬ ЕЁ ГРАФИК
y x 6 x 11x 6
3
2
Решение:
1) Область определения функции: x R
2) При пересечении с осью OY: x 0
y 0 6 0 11 0 6 6
3
2
0; 6
При пересечении с осью OX:
1;0 , 2;0 , 3;0
y 0

4.

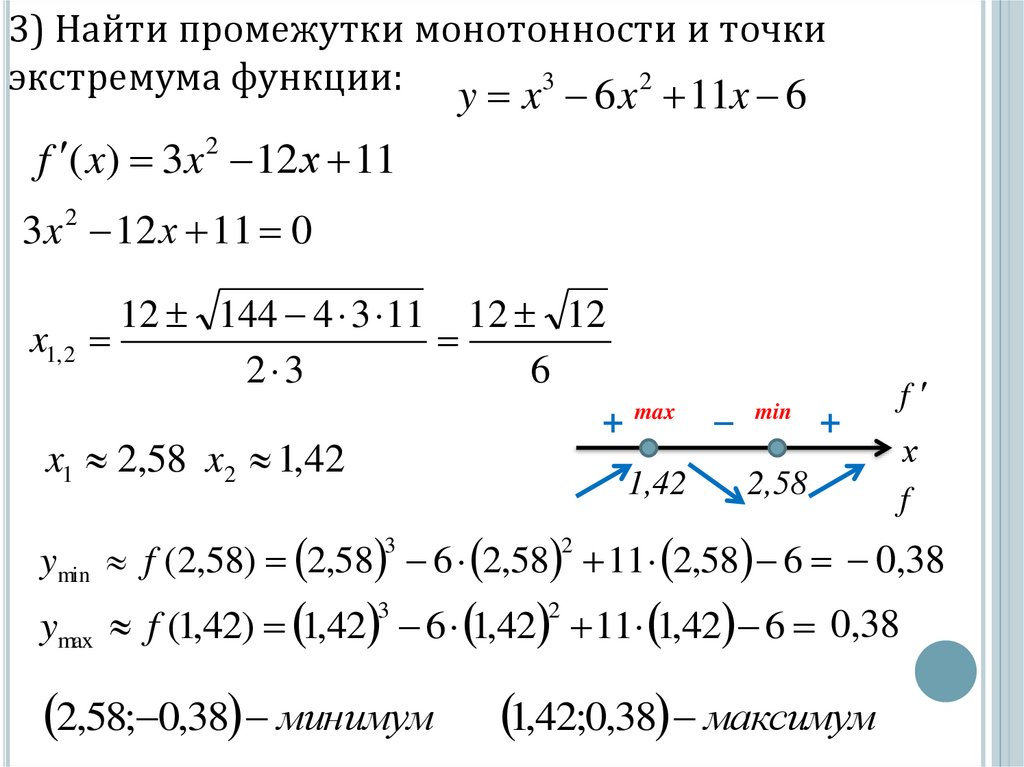
3) Найти промежутки монотонности и точки
экстремума функции: y x 3 6 x 2 11x 6
f ( x) 3x 2 12 х 11
3 x 2 12 х 11 0
12 144 4 3 11 12 12
x1, 2
2 3
6
+
x1 2,58 x2 1,42
max
1,42
–
min
+
2,58
f′
х
f
ymin f (2,58) 2,58 6 2,58 11 2,58 6 0,38
3
2
ymax f (1,42) 1,42 6 1,42 11 1,42 6 0,38
3
2,58; 0,38 минимум
2
1,42;0,38 максимум

5.

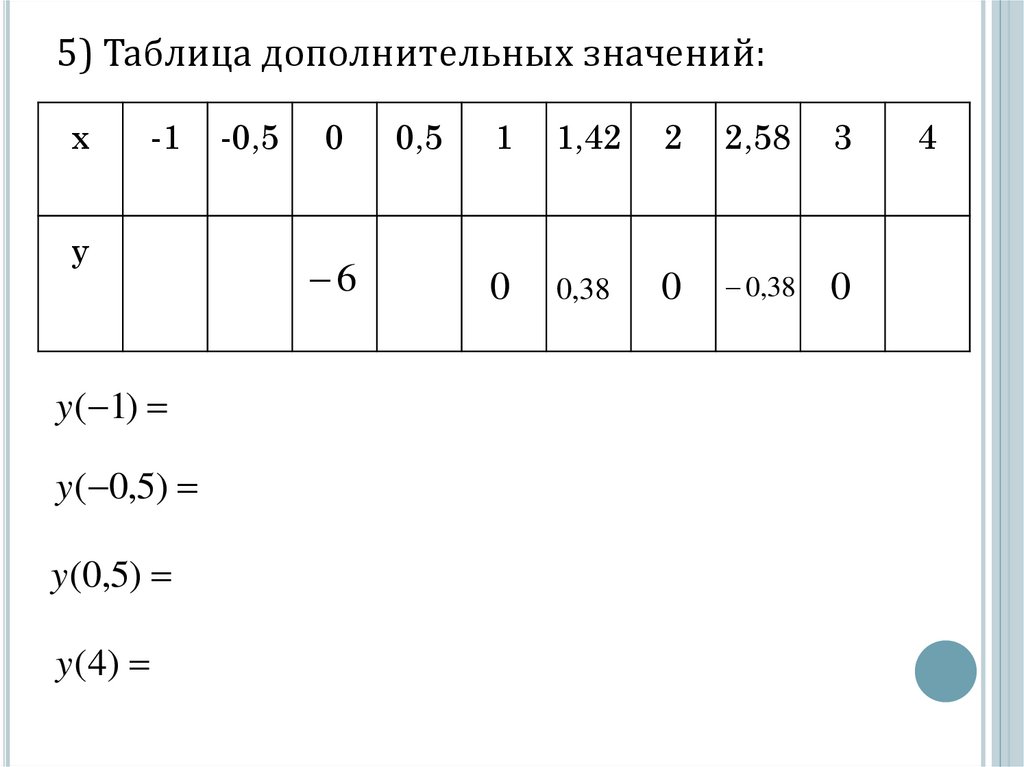
5) Таблица дополнительных значений:
x
-1
y
y ( 1)
y ( 0,5)
y (0,5)
y (4)
-0,5
0
6
0,5
1
1,42
2
2,58
3
0
0,38
0
0,38
0
4

6.

x
y
-1
-0,5
0
0,5
6
24
13,125
1
1,42
2
2,58
3
4
0
0,38
0
0,38
38
5) Таблица дополнительных значений:
6
0
1,875
y ( 1) 1 6 1 11 1 6 24
3
2
y ( 0,5) 0,5 6 0,5 11 0,5 6 13,125
3
2
y (0,5) 0,5 6 0,5 11 0,5 6 1,875
3
2
y(4) 43 6 42 11 4 6 6

7.

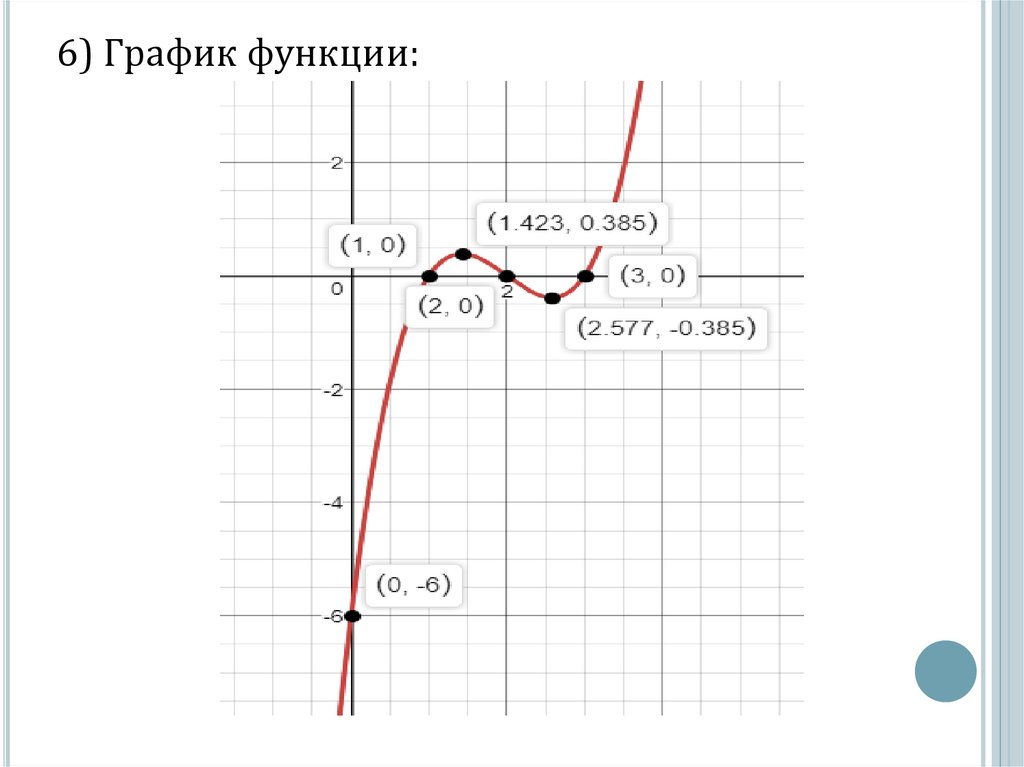
6) График функции:

8. Задание для самостоятельного решения Исследовать функцию с помощью производной и построить её график

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ИССЛЕДОВАТЬ ФУНКЦИЮ С ПОМОЩЬЮ ПРОИЗВОДНОЙ И
ПОСТРОИТЬ ЕЁ ГРАФИК
f ( x) x 3 x 4
3
2