Представление, считывание данных в информационных моделях. Задание №1

1. Представление, считывание данных в информационных моделях. Задание №1

ПРЕДСТАВЛЕНИЕ, СЧИТЫВАНИЕ
ДАННЫХ В ИНФОРМАЦИОННЫХ
МОДЕЛЯХ.
ЗАДАНИЕ №1

2. Данное задание можно разделить на две группы:

Для получения ответа в
задачах из первой группы
нужно найти полное или
частичное соответствие
между графом и таблицей.
В задачах второй группы
предлагается найти
кратчайший (или самый
длинный) маршрут между
двумя пунктами, опираясь на
информационную модель в
виде графа или таблицы.

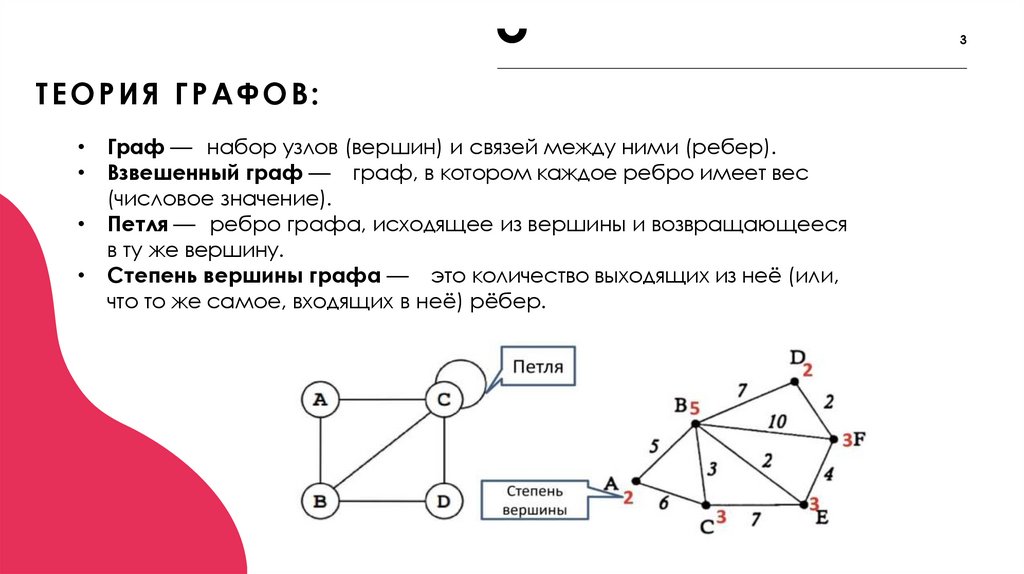
3. Теория графов:

3
ТЕОРИЯ ГРАФОВ:
• Граф — набор узлов (вершин) и связей между ними (ребер).
• Взвешенный граф — граф, в котором каждое ребро имеет вес
(числовое значение).
• Петля — ребро графа, исходящее из вершины и возвращающееся
в ту же вершину.
• Степень вершины графа — это количество выходящих из неё (или,
что то же самое, входящих в неё) рёбер.

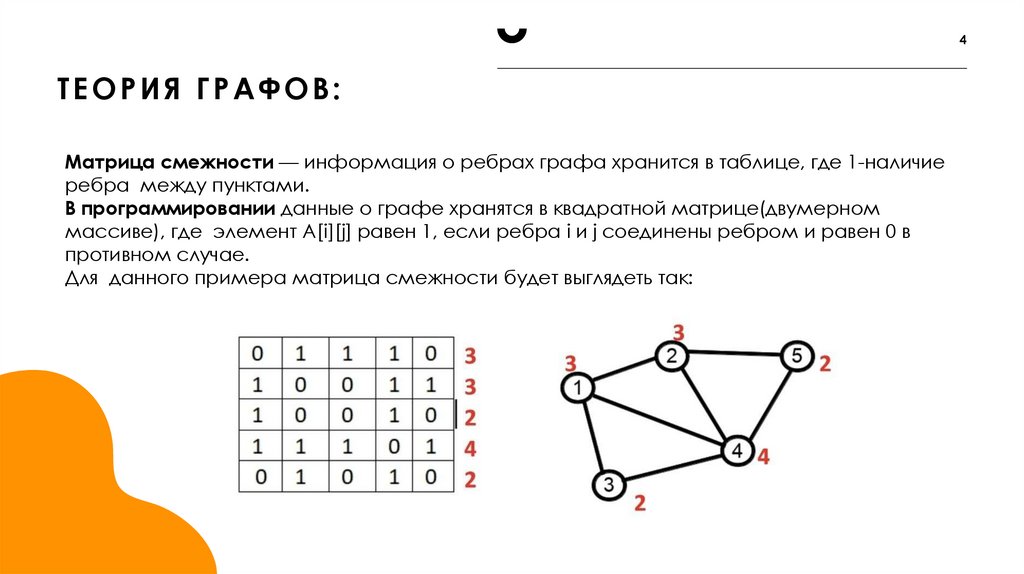
4. Теория графов:

4
ТЕОРИЯ ГРАФОВ:
Матрица смежности — информация о ребрах графа хранится в таблице, где 1-наличие
ребра между пунктами.
В программировании данные о графе хранятся в квадратной матрице(двумерном
массиве), где элемент А[i][j] равен 1, если ребра i и j соединены ребром и равен 0 в
противном случае.
Для данного примера матрица смежности будет выглядеть так:

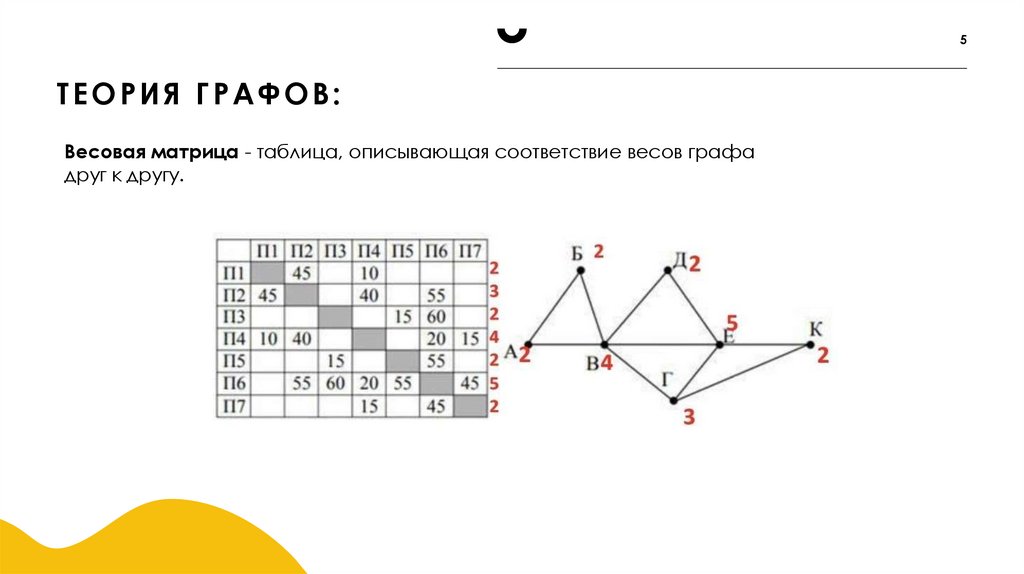
5. Теория графов:

5
ТЕОРИЯ ГРАФОВ:
Весовая матрица - таблица, описывающая соответствие весов графа
друг к другу.

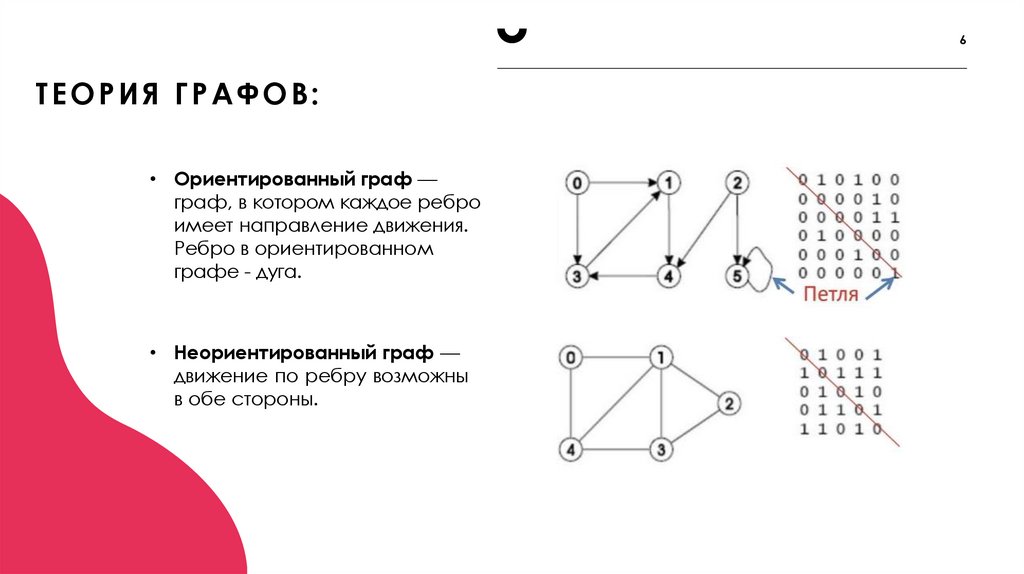
6. Теория графов:

6
ТЕОРИЯ ГРАФОВ:
• Ориентированный граф —
граф, в котором каждое ребро
имеет направление движения.
Ребро в ориентированном
графе - дуга.
• Неориентированный граф —
движение по ребру возможны
в обе стороны.

7. Соответствие между графом и таблицей

СООТВЕТСТВИЕ МЕЖДУ ГРАФОМ И ТАБЛИЦЕЙ

8. Соответствие между графом и таблицей

СООТВЕТСТВИЕ МЕЖДУ ГРАФОМ И ТАБЛИЦЕЙ
1. Поставим в соответствии каждой вершине букву:

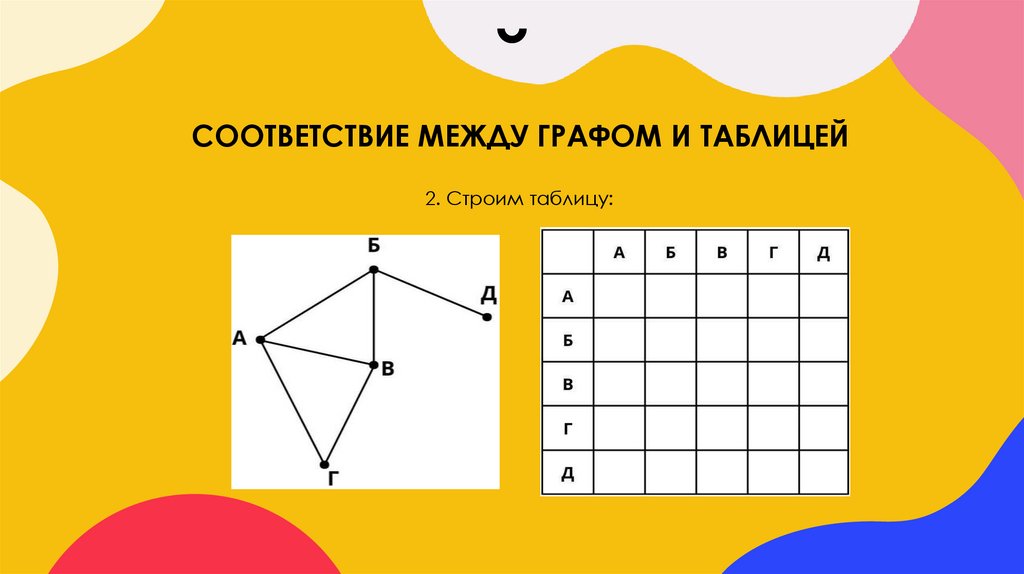
9. Соответствие между графом и таблицей

СООТВЕТСТВИЕ МЕЖДУ ГРАФОМ И ТАБЛИЦЕЙ
2. Строим таблицу:

10. Соответствие между графом и таблицей

СООТВЕТСТВИЕ МЕЖДУ ГРАФОМ И ТАБЛИЦЕЙ
3. Ячейки, стоящие на пересечении строк и столбцов, обозначают
соответствующие ребра графа. В нашем примере есть ребро АБ (отрезок,
соединяющий вершины А и Б). Отметим ячейки таблицы, соответствующие этому
ребру, символом «*». Таких ячеек две, так как граф неориентированный, и мы
можем передвигаться как из А в Б, так и из Б в А.

11. Соответствие между графом и таблицей

СООТВЕТСТВИЕ МЕЖДУ ГРАФОМ И ТАБЛИЦЕЙ
4. Теперь заметим, что нет ребер, соответствующих ячейкам,
стоящим на диагонали таблицы (нет ребра АА, ББ и т.д.).Такие ячейки
принято заштриховывать:

12. Соответствие между графом и таблицей

СООТВЕТСТВИЕ МЕЖДУ ГРАФОМ И ТАБЛИЦЕЙ
5. Отметим в таблице остальные ребра. Заметим, что заштрихованная
диагональ является осью симметрии всей таблицы (верхняя половина таблицы
симметрична нижней относительно диагонали). Это признак соответствия
таблицы неориентированному графу.

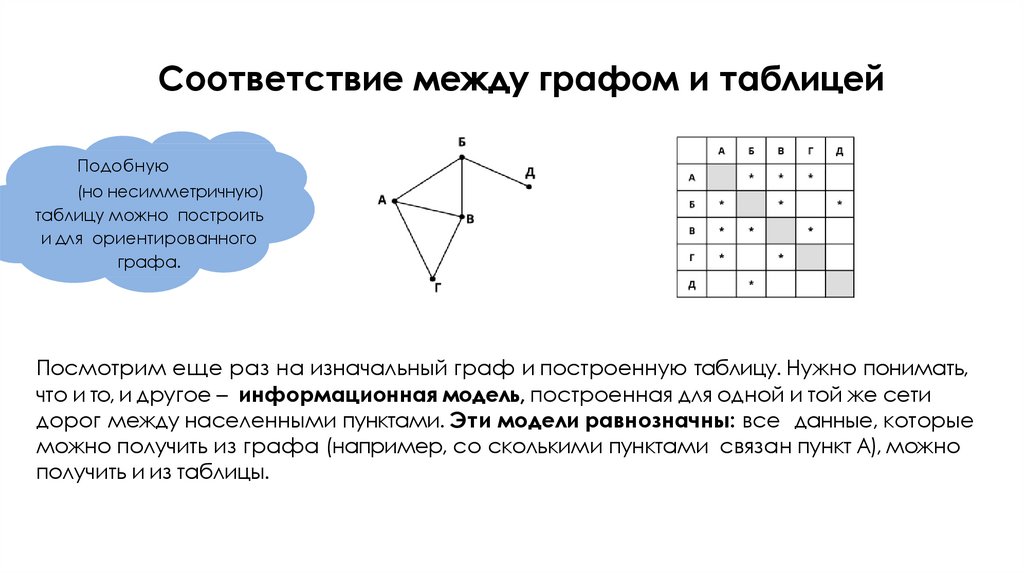
13. Соответствие между графом и таблицей

Подобную
(но несимметричную)
таблицу можно построить
и для ориентированного
графа.
Посмотрим еще раз на изначальный граф и построенную таблицу. Нужно понимать,
что и то, и другое – информационная модель, построенная для одной и той же сети
дорог между населенными пунктами. Эти модели равнозначны: все данные, которые
можно получить из графа (например, со сколькими пунктами связан пункт А), можно
получить и из таблицы.

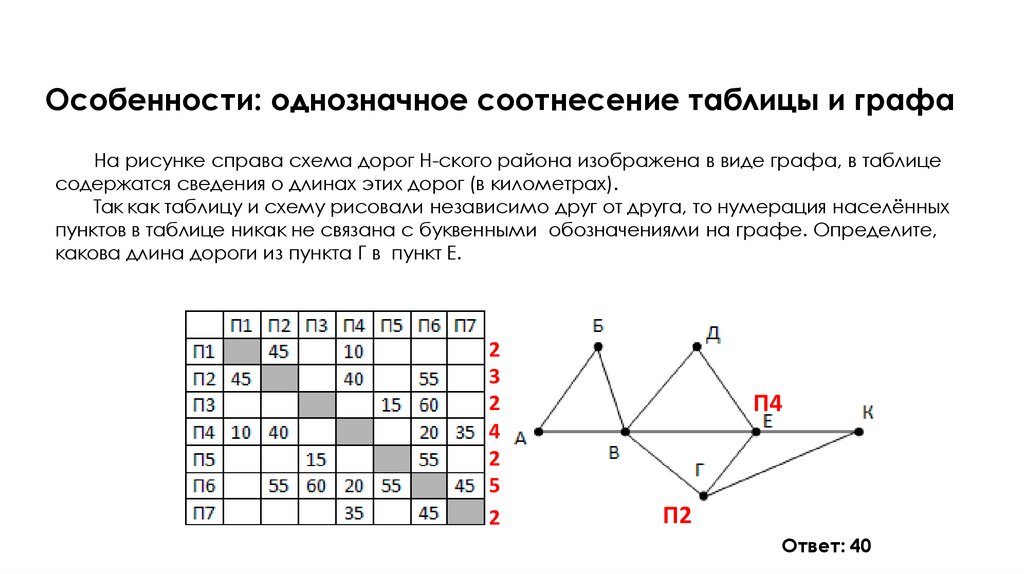
14. Особенности: однозначное соотнесение таблицы и графа

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о длинах этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых
пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите,
какова длина дороги из пункта Г в пункт Е.
2
3
2
4
2
5
2
П4
П2
Ответ: 40

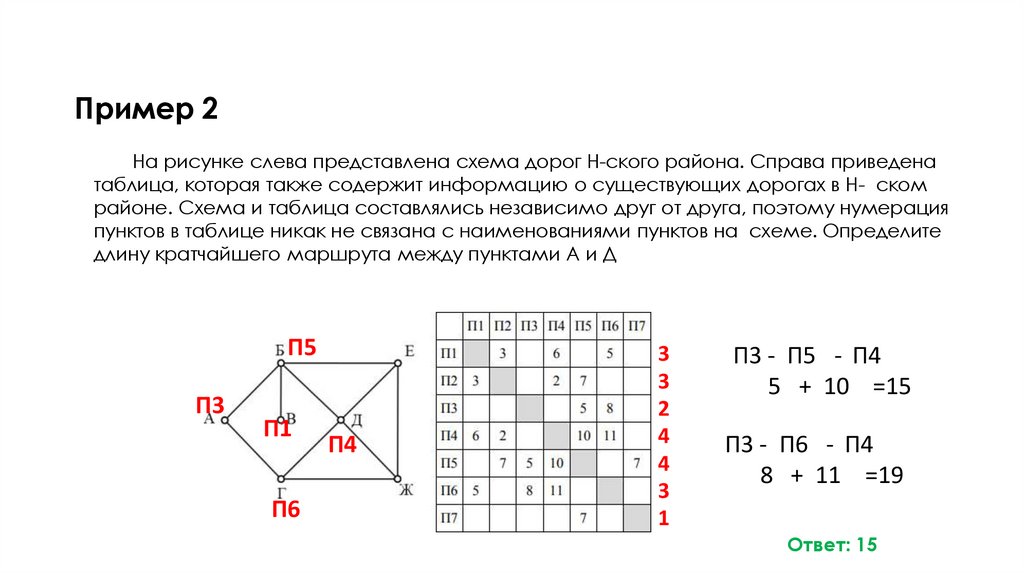
15. Пример 2

На рисунке слева представлена схема дорог Н-ского района. Справа приведена
таблица, которая также содержит информацию о существующих дорогах в Н- ском
районе. Схема и таблица составлялись независимо друг от друга, поэтому нумерация
пунктов в таблице никак не связана с наименованиями пунктов на схеме. Определите
длину кратчайшего маршрута между пунктами А и Д
П5
П3
П1
П6
П4
3
3
2
4
4
3
1
П3 - П5 - П4
5 + 10 =15
П3 - П6 - П4
8 + 11 =19
Ответ: 15

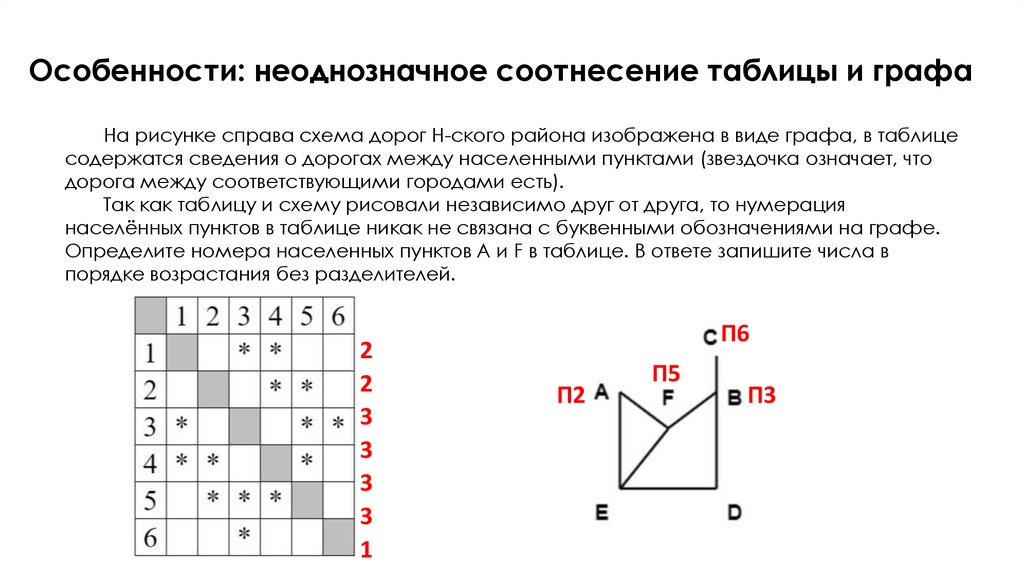
16. Особенности: неоднозначное соотнесение таблицы и графа

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о дорогах между населенными пунктами (звездочка означает, что
дорога между соответствующими городами есть).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите номера населенных пунктов A и F в таблице. В ответе запишите числа в
порядке возрастания без разделителей.
2
2
3
3
3
3
1
П6
П2
П5
П3

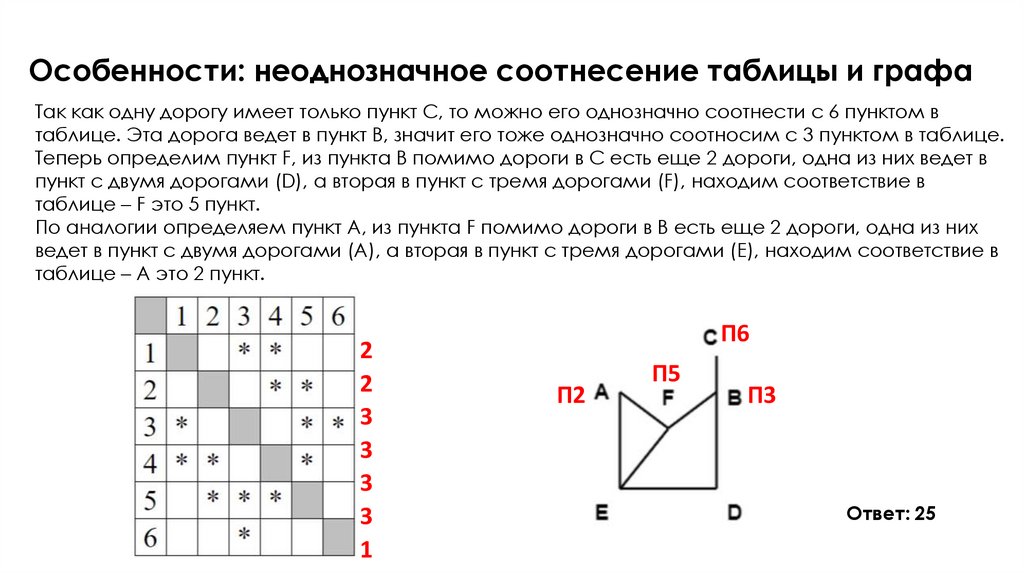
17. Особенности: неоднозначное соотнесение таблицы и графа

Так как одну дорогу имеет только пункт C, то можно его однозначно соотнести с 6 пунктом в
таблице. Эта дорога ведет в пункт B, значит его тоже однозначно соотносим с 3 пунктом в таблице.
Теперь определим пункт F, из пункта B помимо дороги в C есть еще 2 дороги, одна из них ведет в
пункт с двумя дорогами (D), а вторая в пункт с тремя дорогами (F), находим соответствие в
таблице – F это 5 пункт.
По аналогии определяем пункт A, из пункта F помимо дороги в B есть еще 2 дороги, одна из них
ведет в пункт с двумя дорогами (A), а вторая в пункт с тремя дорогами (E), находим соответствие в
таблице – A это 2 пункт.
2
2
3
3
3
3
1
П6
П2
П5
П3
Ответ: 25

18. Спасибо

СПАСИБО
Практическое задание прикреплено в уроке