Марковские подстановки. Нормальные алгоритмы. Правила выполнения нормальных алгоритмов. Принцип нормализации Маркова

1. Марковские подстановки. Нормальные алгоритмы. Правила выполнения нормальных алгоритмов. Принцип нормализации Маркова.

Пояркова Анна Вячеславовна

2. Введение

3. Кто такой Марков и его вклад в теорию алгоритмов

Александр Александрович Марков, выдающийся
российский математик и логик, который сделал
значительный вклад в теорию алгоритмов.
Кто такой
Марков и его
вклад в теорию
алгоритмов
Краткая биография:
Марков родился в 1905 году и окончил Московский
государственный университет. Он стал профессором и
работал в области теории алгоритмов и математической
логики.
Его работы охватывают широкий спектр тем, включая
марковские подстановки и нормальные алгоритмы.

4.

Вклад в теорию алгоритмов:
Марков разработал концепцию марковских подстановок,
которая позволяет формализовать процесс вычислений.
Это стало основой для дальнейших исследований в области
вычислений.
Его работы по нормальным алгоритмам помогли
установить критерии, по которым можно оценивать
алгоритмы на завершенность и корректность. Это стало
важным шагом в развитии теории вычислений.
Влияние на науку:
Идеи Маркова легли в основу таких понятий, как
вычислимость и алгоритмическая сложность, которые
являются ключевыми в современных исследованиях. Его
работы остаются актуальными и сегодня, особенно в
контексте изучения алгоритмов и их применения в
различных областях.

5.

Основные достижения:
Он создал марковские подстановки, которые стали основой
для многих алгоритмических моделей.
Разработал нормальные алгоритмы, которые помогают
оценивать алгоритмическую сложность и корректность.
Написал более 100 научных работ, которые оказали
влияние на развитие теории вычислений.

6. Вопрос

Как вы думаете, почему изучение алгоритмов так
важно в современном мире?

7. Марковские подстановки

8. Определение марковских подстановок

Марковская подстановка — это формальная система,
состоящая из алфавита, строк и правил подстановки,
которые позволяют преобразовывать строки в другие
строки. Основная идея заключается в том, что мы можем
применять определенные правила к строкам, чтобы
получить новые строки, и этот процесс может
повторяться.

9.

Компоненты марковской подстановки:
Алфавит: Набор символов, из которых формируются
строки. Например, алфавит может состоять из букв {A, B,
C}.
Строки: Последовательности символов, составленные из
алфавита. Например, строка "ABAC" состоит из символов
A, B и C.
Правила подстановки: Набор правил, которые
определяют, как строки могут быть преобразованы.
Правила имеют вид "X → Y", что означает, что символ X
может быть заменен на символ Y.

10.

Подстановки Интересной особенностью нормальных
алгоритмов Маркова (НАМ) является то, что в них
используется лишь одно элементарное действие – так
называемая подстановка, которая определяется
следующим образом.

11. Примеры марковских подстановок

Формулой подстановки называется запись вида α→β
(читается «α заменить на β»), где α и β – любые слова
(возможно, и пустые). При этом α называется левой
частью формулы, а β – правой частью.
Примеры
марковских
подстановок
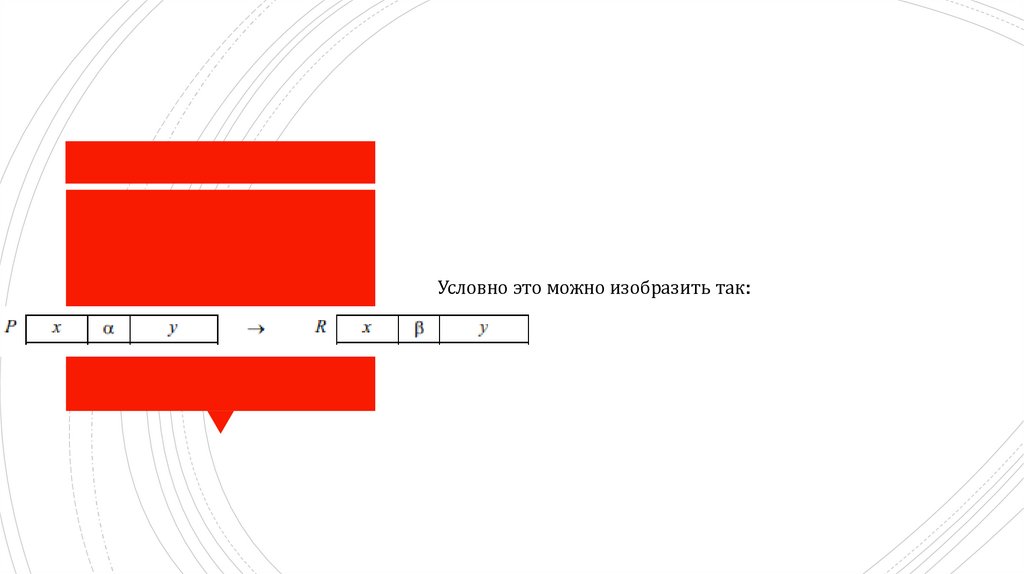
Сама подстановка (как действие) задается формулой
подстановки и применяется к некоторому слову Р. Суть
операции сводится к тому, что в слове Р отыскивается
часть, совпадающая с левой частью этой формулы (т.е. с
α), и она заменяется на правую часть формулы (т.е. на β).
При этом остальные части слова Р (слева и справа от α)
не меняются. Получившееся слово R называют
результатом подстановки.

12.

Условно это можно изобразить так:

13.

Необходимые уточнения:
1. Если левая часть формулы подстановки входит в слово
Р, то говорят, что эта формула применима к Р. Но если α
не входит в Р, то формула считается неприменимой к Р,
и подстановка не выполняется.
2. Если левая часть α входит в Р несколько раз, то на
правую часть β, по определению, заменяется только
первое вхождение α в Р:

14.

3. Если правая часть формулы подстановки – пустое
слово, то подстановка α→ сводится к вычеркиванию
части α из Р (отметим попутно, что в формулах
подстановки не принято как-либо обозначать пустое
слово):
4. Если в левой части формулы подстановки указано
пустое слово, то подстановка →β сводится, по
определению, к приписыванию β слева к слову P:
Из этого правила вытекает очень важный факт: формула
с пустой левой частью применима к любому слову.
Отметим также, что формула с пустыми левой и правой
частями не меняет слово.

15. Определение НАМ

Нормальным алгоритмом Маркова (НАМ) называется
непустой конечный упорядоченный набор формул
подстановки:
Определение
НАМ
В этих формулах могут использоваться два вида
стрелок: обычная стрелка (→) и стрелка «с хвостиком»
(
). Формула с обычной стрелкой называется
обычной формулой, а формула со стрелкой «с
хвостиком» – заключительной формулой. Разница
между ними объясняется чуть ниже. Записать
алгоритм в виде НАМ – значит предъявить такой набор
формул.

16. Правила выполнения НАМ

Прежде всего, задается некоторое входное слово Р. Где
именно оно записано – не важно, в НАМ этот вопрос не
оговаривается.
Работа НАМ сводится к выполнению последовательности
Правила
выполнения
НАМ
шагов. На каждом шаге входящие в НАМ формулы
подстановки просматриваются сверху вниз и выбирается
первая из формул, применимых к входному слову Р, т.е.
самая верхняя из тех, левая часть которых входит в Р.
Далее выполняется подстановка согласно найденной
формуле. Получается новое слово Р′.
На следующем шаге это слово Р′ берется за исходное и к
нему применяется та же самая процедура, т.е. формулы
снова просматриваются сверху вниз начиная с самой
верхней и ищется первая формула, применимая к слову Р′,
после чего выполняется соответствующая подстановка и
получается новое слово Р′′. И так далее:

17.

Следует обратить особое внимание на тот факт, что на каждом шаге
формулы в НАМ всегда просматриваются начиная с самой первой.
Необходимые уточнения:
1. Если на очередном шаге была применена обычная формула (α→β), то
работа НАМ продолжается.
2. Если же на очередном шаге была применена заключительная
формула (α
β), то после её применения работа НАМ прекращается.
То слово, которое получилось в этот момент, и есть выходное слово, т.е.
результат применения НАМ к входному слову.
Как видно, разница между обычной и заключительной формулами
подстановки проявляется лишь в том, что после применения обычной
формулы работа НАМ продолжается, а после заключительной формулы
– прекращается. 3. Если на очередном шаге к текущему слову
неприменима ни одна формула, то и в этом случае работа НАМ
прекращается, а выходным словом считается текущее слово.
Таким образом, НАМ останавливается по двум причинам: либо была
применена заключительная формула, либо ни одна из формул не
подошла. То и другое считается «хорошим» окончанием работы НАМ. В
обоих случаях говорят, что НАМ применúм к входному слову.

18. Примеры на составление НАМ

Рассмотрим примеры, в которых демонстрируются
типичные приёмы составления НАМ.
Как и в случае машины Тьюринга, для сокращения
формулировки задач будем использовать следующие
соглашения:
Примеры на
составление
НАМ
– буквой Р будем обозначать входное слово;
– буквой А будем обозначать алфавит входного слова, т.е.
набор тех символов, которые и только которые могут
входить во входное слово Р (но в процессе выполнения
НАМ в обрабатываемых словах могут появляться и
другие символы).
Кроме того, в примерах будем справа от формул
подстановки указывать их номера. Эти номера не входят
в формулы, а нужны для ссылок на формулы при показе
пошагового выполнения НАМ.

19. Пример. (вставка и удаление символов)

А={a,b,c,d}. В слове Р требуется заменить первое
вхождение подслова bb на ddd и удалить все вхождения
символа c.
Например: abbcabbca → adddabba
Решение.
Пример. (вставка
и удаление
символов)
Прежде всего отметим, что в НАМ, в отличие от машины
Тьюринга, легко реализуются вставки и удаления
символов. Вставка новых символов в слово – это замена
некоторого подслова на подслово с бóльшим числом
символов; например, с помощью формулы bb→ddd два
символа будут заменены на три символа. При этом не
надо заботиться о том, чтобы предварительно
освободить место для дополнительных символов, в НАМ
слово раздвигается автоматически

20.

Удаление же символов – это замена некоторого подслова
на подслово с меньшим числом символов; например,
удаление символа c реализуется формулой c→ (с пустой
правой частью). При этом никаких пустых позиций
внутри слова не появляется, сжатие слова в НАМ
происходит автоматически. С учётом сказанного нашу
задачу должен, казалось бы, решать такой НАМ:
Однако это не так. Проверим этот НАМ на входном слове
abbcabbca (над стрелками указаны номера
применённых формул, а в словах слева от стрелок
подчёркнуты для наглядности те части, к которым были
применены эти формулы):

21.

Как видно, заменив первое вхождение bb на ddd, этот
НАМ не перешёл сразу к удалению символов c, а стал
заменять и другие вхождения bb. Почему? Напомним, что
на каждом шаге работы НАМ формулы подстановки
всегда просматриваются сверху вниз начиная с первой из
них. Поэтому, пока применима первая формула, она и
будет применяться, блокируя доступ к остальным
формулам. Этот означает, что в НАМ важен порядок
перечисления формул подстановки.
Учтём это и переставим наши две формулы:
Проверим этот новый алгоритм на том же входном слове:

22.

Итак, НАМ сначала удалил все символы c и только затем
заменил первое вхождение bb на ddd. Однако НАМ на
этом не остановился и стал заменять остальные
вхождения bb. Почему? Дело в том, что, пока применима
хотя бы одна формула, НАМ продолжает свою работу. Но
нам этого не надо, поэтому мы должны принудительно
остановить НАМ после того, как он заменил первое
вхождение bb. Вот для этого и нужны заключительные
формулы подстановки, после применения которых НАМ
останавливается. Следовательно, в нашем алгоритме
обычную формулу bb→ddd надо заменить на
заключительную формулу bb
ddd
Вот теперь наш алгоритм будет работать правильно:

23.

Слово, которое получилось после применения
заключительной формулы (2), является выходным
словом, т.е. результатом применения НАМ к заданному
входному слову. Проверим наш НАМ ещё и на входном
слове, в которое не входит bb:
К последнему слову (dab) неприменима ни одна
формула, поэтому, согласно определению НАМ,
алгоритм останавливается и это слово объявляется
выходным.