Алгоритмы генерации псевдослучайной последовательности чисел. Тема 5.1

1. Тема 5.1 Алгоритмы генерации псевдослучайных последовательностей

1

2. Псевдослучайная последовательность

Зачем вообще разговаривать о случайных числах при
обсуждении криптографии? В каждом компиляторе есть
датчик случайных чисел, но, к сожалению, большинство
таких датчиков почти наверняка криптографически нестойки
и, возможно, даже не очень случайны.
Почему? Такие датчики не случайны, т.к. в этом нет особой
потребности. Большинству обычных приложений не
требуется большого количества случайных чисел
(симуляторы, компьютерные игры и т.п.).
Но криптография особенно чувствительна к свойствам
датчиков случайных чисел.
2

3. Псевдослучайная последовательность

Зачастую криптографическая стойкость алгоритма напрямую
зависит от случайности датчика случайных чисел.
Основная сложность генерации простых чисел на компьютере
в том, что компьютеры детерминистичны по своей сути.
Компьютер может находиться только в конечном количестве
состояний (количество состояний огромно, но все-таки
конечно).
любой датчик случайных чисел по определению
периодичен. Все периодическое – предсказуемо не
случайно.
Лучшее, что может произвести компьютер – это
псевдослучайная последовательность.
3

4. Псевдослучайная последовательность

Что такое псевдослучайная последовательность? Нечто сложно
определяемое (мы не будем давать точного определения).
Период такой последовательности должен быть таким,
чтобы конечная последовательность разумной длины не
была периодической.
Относительно короткие непериодические
подпоследовательности должны быть как можно более
неотличимы от случайных последовательностей, в
частности, соответствовать различным критериям
случайности.
4

5. Псевдослучайная последовательность

Определение 1. Генератор последовательности
псевдослучаен, если он выглядит случайным, т.е. проходит
все статистические тесты случайности (начиная с χ2 –
статистику Пирсона – см. Кнут. т.2, стр. 52 и далее).
Для криптографических приложений статистической
случайности недостаточно, хотя это и необходимое
свойство.
Определение 2. Последовательность называется
криптографически надежной псевдослучайной
последовательностью (KSPRSG), если она непредсказуема,
т.е. вычислительно неосуществимо предсказать следующий
бит, имея полное знание алгоритма (или аппаратуры) и всех
предшествующих битов потока.
Они тоже подвержены криптоанализу – как любой
шифрирующий алгоритм.
5

6. Псевдослучайная последовательность

Наконец, наиболее сильное определение:
Определение 3. Генератор последовательности называется
случайным, если он не может быть достоверно
воспроизведен, т.е. дважды запуская генератор с абсолютно
одинаковыми исходными данными (по крайней мере, на
пределе человеческих возможностей), мы получим
случайные различные последовательности.
6

7. Псевдослучайная последовательность

Вопрос существования случайных последовательностей –
философский вопрос.
Мы знаем, что на микроуровне случайность существует
(квантовая механика), но сохранит ли эта случайность при
переходе на макроуровень.
Дополнительное свойство случайной последовательности:
случайная последовательность не может быть сжата.
KSPRSG не может быть сжаты (на практике).
Генератор со своими определениями 1-3 достаточно хорош для
одноразовых блокнотов, генерации ключей и любых других
криптографических приложений.
Теперь рассмотрим эти категории генераторов подробнее.
7

8. Псевдослучайная последовательность

Известно, что проблема генерации случайной
последовательности с произвольным законом распределения
вероятностей сводится к проблеме генерации так
называемой равномерно распределенной случайной
последовательности (РРСП), или, как ее часто называют в
криптографических приложениях, чисто случайной
последовательности.
8

9. Псевдослучайная последовательность

Определение 4. Равномерно распределенная случайная
последовательность – это случайная последовательность х1,
х2, …, xi, xi+1, … со значениями в дискретном множестве
A={0, 1, …, N-1}, определенная на вероятностном
пространстве ( , F, P) и удовлетворяющая двум свойствам:
– C1: для n и произвольных значений индексов 1≤ t1 <
…< tn случайные величины xt1, …, xtn A независимы в
совокупности;
– C2: для номера t случайная величина xt имеет
дискретное равномерное на A распределение
вероятностей:
1
P x i i , i A
N
9

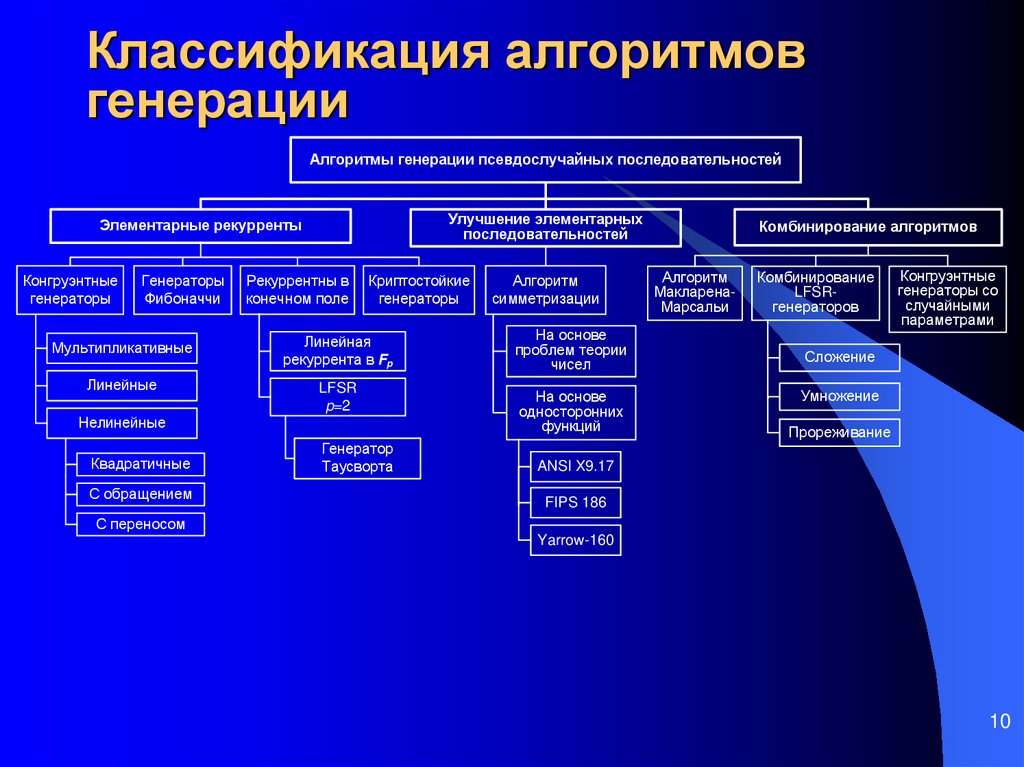
10. Классификация алгоритмов генерации

Алгоритмы генерации псевдослучайных последовательностей
Улучшение элементарных
последовательностей
Элементарные рекурренты
Конгруэнтные
генераторы
Генераторы
Фибоначчи
Рекуррентны в
конечном поле
Криптостойкие
генераторы
Алгоритм
симметризации
Мультипликативные
Линейная
рекуррента в Fp
На основе
проблем теории
чисел
Линейные
LFSR
p=2
На основе
односторонних
функций
Нелинейные
Квадратичные
С обращением
Генератор
Таусворта
Комбинирование алгоритмов
Алгоритм
МакларенаМарсальи
Комбинирование
LFSRгенераторов
Конгруэнтные
генераторы со
случайными
параметрами
Сложение
Умножение
Прореживание
ANSI X9.17
FIPS 186
С переносом
Yarrow-160
10

11. Классификация алгоритмов генерации

Выделяют три основных подхода к построению алгоритмов
генерации:
1) Прямые методы построения элементарных рекуррентных
последовательностей:
xt= f(xt-1, xt-2, …, xt-m) : Am A,
проходящих статистические тесты;
2) Методы «улучшения элементарных
последовательностей», заключающиеся в специальных
функциональных преобразованиях этих
последовательностей для уменьшения отклонения их
статистических свойств от свойств РРСП;
3) Комбинирование алгоритмов генерации, построенных с
помощью 1-го или 2-го подхода.
11

12. 2.1. Линейные и мультипликативные конгруэнтные генераторы

12

13. Линейные конгруэнтные генераторы

Линейным конгруэнтным генератором (ЛКГ) с параметрами
(x0, a, c, N) называется программный генератор РРСП,
порождающий псевдослучайную последовательность x1,
x2, …, A, A={0, 1, …, N-1}, с помощью рекуррентного
соотношения
xt+1 = (axt + c) mod N, t=0, 1,…
(1)
Параметры генератора имеют следующий смысл:
x0 A - начальное, или стартовое, значение (seed);
a A \ {0} – ненулевой множитель;
c A – приращение;
N – модуль, равный мощности алфавита A.
13

14. Мультипликативные конгруэнтные генераторы

Если приращение с=0, то генератор (1) называется
мультипликативным конгруэнтным генератором (МКГ),
а если с 0, то смешанным конгруэнтным генератором
(СКГ).
14

15. Свойства псевдослучайной последовательности, порождаемой ЛКГ

С1. Для общего члена последовательности (1) справедлива
формула
t
at 1
xt a x0
c mod N , t 1
a 1
С2. Найдется номер A, начиная с которого
последовательность (1) «зацикливается» с периодом
T N- .
С3. Для любого k 2 подпоследовательность x0, xk, x2k, x3k, …
A, полученная из (1) удалением всех членов, не кратных
k, оказывается псевдослучайной последовательностью,
порожденной ЛКГ (1), с параметрами (x0, a’, c’, N), где
a’= ak mod N,
c’= (c (ak-1) / (a-1)) mod N.
15

16. Свойства псевдослучайной последовательности, порождаемой ЛКГ

С4. Псевдослучайная последовательность (1), порождаемая
ЛКГ, достигает максимального значения периода Tmax = N
( =0) тогда и только тогда, когда выполнены условия;
c и N – взаимно простые;
число b=a –1 кратно p для любого простого числа p<N,
являющегося делителем N;
число b кратно 4, если N кратно 4.
С5. Для МКГ (c=0), если x0 и N – взаимно простые, a –
первообразный элемент по модулю N, а (N) –
максимально возможный порядок по модулю N, то
псевдослучайная последовательность имеет
максимальный период Tmax = (N).
16

17. Свойства псевдослучайной последовательности, порождаемой ЛКГ

С6. Для МКГ, если N=10q, q 5 и x0 не кратно 2 или 5, то
максимально возможное значение периода
Tmax=5 10q-2=N/20 достигается тогда и только тогда, когда
вычет a mod 200 принимает одно из 32 следующих
«магических» значений:
3, 11, 13, 19, 21, 27, 29, 37, 53, 59, 61, 67, 77, 83, 91, 109,
117, 123, 131, 133, 139, 141, 147, 163, 171, 173, 179, 181,
187, 189, 197.
С7. Для МКГ, если N=2q, q 4, то максимально возможное
значение периода Tmax=2q-2=N/4 достигается, если x0 1 –
нечетно и вычет a mod 8 {3, 5}.
17

18. Свойства псевдослучайной последовательности, порождаемой ЛКГ

С8. Для МКГ, если x0 0, N – простое число и справедливо
разложение на множители: N–1=p1m1… psms, где p1, …, ps –
простые числа, m1,…, ms , то максимально возможное
значение периода Tmax=N–1 достигается для случая, когда
a (N–1)/pj 1 (mod N), j=1, …, s.
С9. «Слабость» ЛКГ и МКГ заключается в том, что если
рассматривать последовательные биграммы (z1(t), z2(t)):
z1(t)=xt, z2(t)=xt-1, то точки zt= (z1(t), z2(t)), t=1, 2, …, на
плоскости R2 будут лежать на прямых из семейства
z2=az1+c–k N, k=0, 1, …
18

19. 3.2. Нелинейные конгруэнтные генераторы

19

20.

Свойство С9 ЛКГ и МКГ псевдослучайных
последовательностей представляет слабость этих
генераторов и может активно использоваться для
построения криптоатак в целях оценки параметров a, c, x0.
Для устранения этого недостатка используют нелинейные
конгруэнтные генераторы псевдослучайных
последовательностей.
20

21. Квадратичный конгруэнтный генератор

Этот алгоритм генерации псевдослучайной
последовательности xt A, A={0, 1, …, N-1} определяется
квадратичным рекуррентным соотношением
xt+1 = (d xt2 + axt + c) mod N, t=0, 1,…
(2)
где x0, a, c, d A – параметры генератора.
Выбор этих параметров осуществляется на основе следующих
двух свойств последовательности (2).
21

22. Свойства квадратичного конгруэнтного генератора

С1. Квадратичная конгруэнтная последовательность (2) имеет
максимально возможное значение периода Tmax=N тогда и
только тогда, когда выполнены следующие условия:
1) c, N – взаимно простые числа;
2) d, a–1 – кратны p, где p – любой нечетный простой
делитель N;
3) d – четное число, причем
( a 1) mod 4, если N кратно 4,
d
( a 1) mod 2, если N кратно 2;
4) если N кратно 9, то либо d mod 9 =0, либо d mod 9 =1 и
cd mod 9 =6.
22

23. Свойства квадратичного конгруэнтного генератора

С2. Если N=2q, q 2, то наибольший период Tmax=2q
достигается тогда и только тогда, когда a, c – нечетны, d –
четно и a удовлетворяет соотношению
a = (d+1) mod 4.
23

24. Генератор Эйхенауэра-Лена с обращением

Псевдослучайная нелинейная конгруэнтная
последовательность Эйхенауэра-Лена с обращением
определяется следующим нелинейным рекуррентным
соотношением (t=0, 1, 2, …):
(axt 1 c ) mod N , если xt 1,
xt 1
c, если xt 0,
(3)
где x0, a, c A – параметры генератора; xt-1 A – обратный к xt
элемент по модулю N, т.е. xt-1xt 1(mod N) .
24

25. Свойство генератора Эйхенауэра-Лена с обращением

Свойство генератора ЭйхенауэраЛена с обращением
С3. Если N=2q, a, x0 – нечетны, c – четно, то генератор (3)
имеет максимально возможный период Tmax=2q–1 тогда и
только тогда, когда
a 1 mod 4, c 2 mod 4.
25

26. Конгруэнтный генератор, использующий умножение с переносом

При этом нелинейная конгруэнтная псевдослучайная
последовательность определяется рекуррентным
соотношением
xt+1 = (axt + ct ) mod N, t=0, 1,…
(4)
где, в отличие от (2), «приращение» ct = c(xt–1, xt–2, …, x0)
изменяется во времени и зависит от указанных аргументов
нелинейно:
axt 1 ct 1
ct
(5)
N
Параметрами нелинейного конгруэнтного генератора (4-5)
являются x0, c0, a, N. Рекомендации по выбору этих
параметров даются в доп. литературе.
26

27. 3.3. Реккуренты в конечном поле

27

28.

Обобщением МКГ является линейная реккурентная
последовательность порядка k 1 над конечным полем Fp
(p – простое число):
xt+1 = (a1xt + a2xt–1 +…+ akxt–k+1) mod p, t=0, 1,…, (6)
где a1, a2, …, ak A={0, 1, …, p–1 } – коэффициенты
рекурренты, а x0, x–1, …, x–k+1 A – начальные значения
рекурренты.
Наряду с этими значениями параметрами генератора
псевдослучайной последовательности (6) являются числа
p, k.
28

29. Рекурренты в конечном поле

Начальные значения x0, x–1, …, x–k+1 A выбираются
произвольно так, чтобы не обращались в ноль
одновременно.
Коэффициенты рекурренты a1, a2, …, ak A выбираются таким
образом, чтобы порождающий полином
f(x) = xk – a1xk –1 –…– ak –1x –ak
(7)
являлся примитивным многочленом по модулю p, т.е.
многочлен (7) имел корень x*, являющийся первообразным
Fp k
элементом поля
.
При таком выборе параметров достигается максимально
возможный период Tmax=pk–1 псевдослучайной
последовательности (7).
29

30. Рекурренты в конечном поле

Примеры эффективно реализуемых на компьютере алгоритмов
генерации вида (7) с периодом Tmax 296:
xt+1 = (1176xt + 1476xt–1 + 1776xt–2) mod (232 – 5);
xt+1 = 213 (xt + xt–1 + xt–2) mod (232 – 5);
xt+1 = (1995xt + 1998xt–1 + 2001xt–2) mod (235 – 849);
xt+1 = 219 (xt + xt–1 + xt–2) mod (235 – 1629).
30

31. Рекурренты в конечном поле

Для повышения качества псевдослучайных
последовательностей в линейную рекурренту (7) вводится
нелинейное приращение ct (как и в конгруэнтном
генераторе):
xt+1 = (a1xt + a2xt–1 +…+ akxt–k+1 + ct) mod p, t=0, 1,…, (8)
где приращение-перенос
ct = с(xt–1, xt–2, …, x0 , x–1, …, x–k+1 ) mod p A
зависит от своих аргументов нелинейно согласно
рекуррентному соотношению
ct = (a1xt + a2xt–1 +…+ akxt–k+1 + ct –1)/p
(9)
Примером рекуррентного генератора с переносом (8-9)
является генератор с периодом Tmax 2158:
xt+1 = (5115xt + 1776xt–1 + 1492xt–2 + 2111111111xt–3 + ct) mod 232.
(10)
31

32. 3.4. Последовательности, порождаемые линейными регистрами сдвига с обратной связью (LFSR)

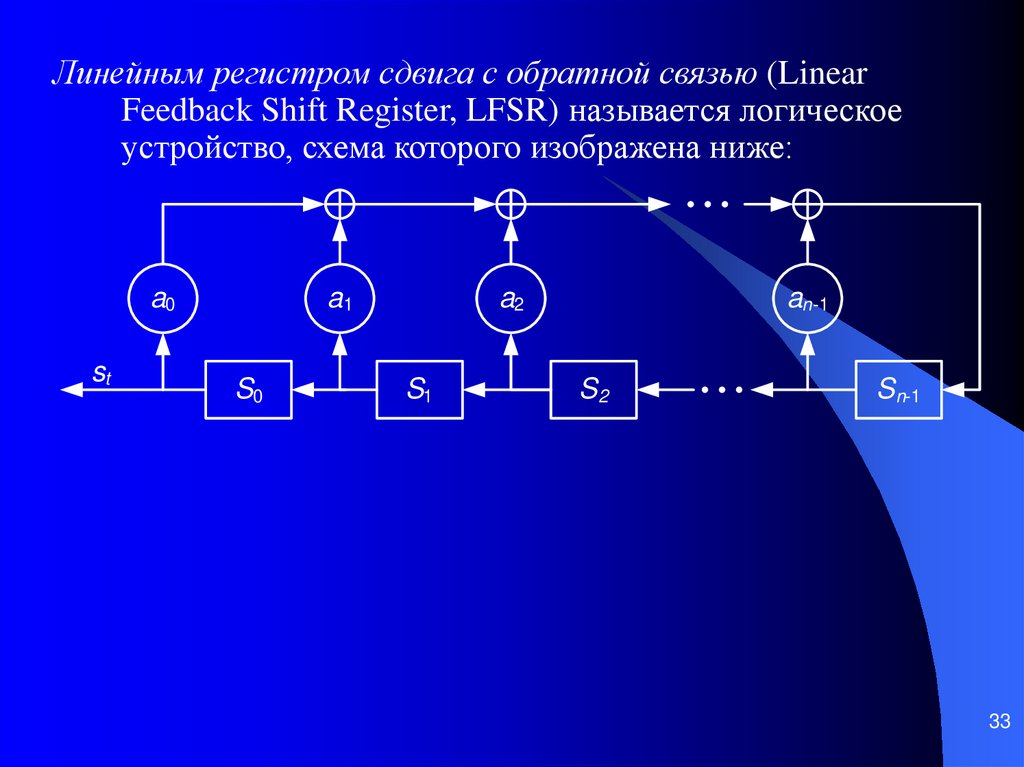
32

33.

Линейным регистром сдвига с обратной связью (Linear
Feedback Shift Register, LFSR) называется логическое
устройство, схема которого изображена ниже:
a0
st
a1
S0
a2
S1
an-1
S2
Sn-1
33

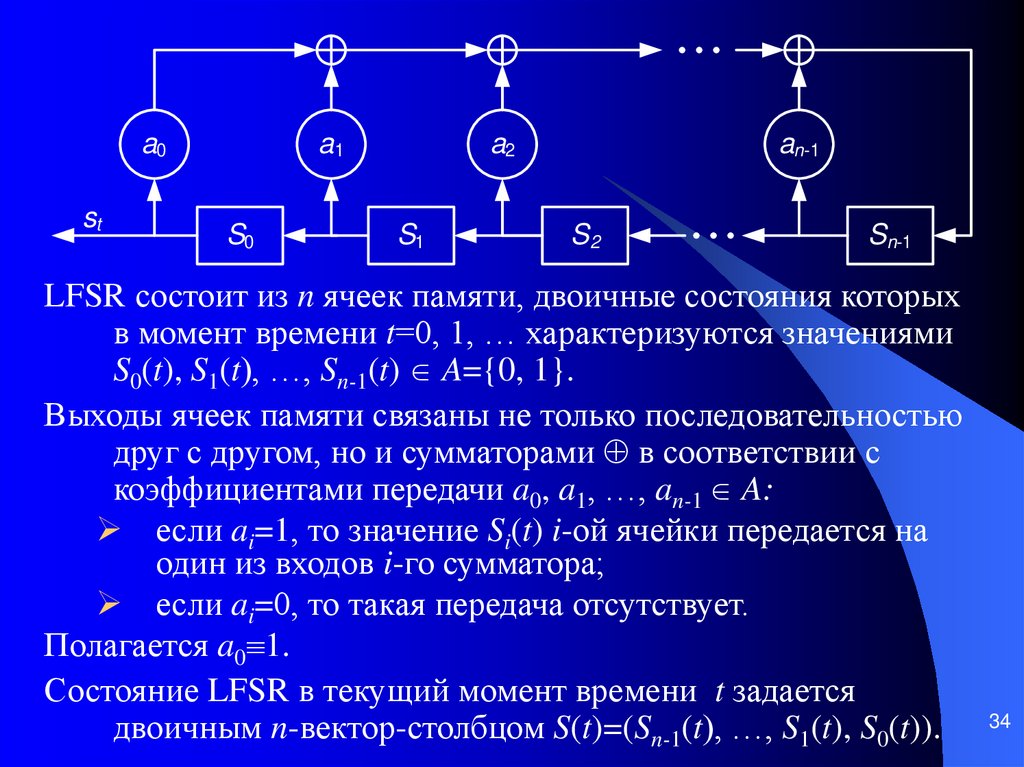
34.

a0
st
a1
S0
a2
S1
an-1
S2
Sn-1
LFSR состоит из n ячеек памяти, двоичные состояния которых
в момент времени t=0, 1, … характеризуются значениями
S0(t), S1(t), …, Sn-1(t) A={0, 1}.
Выходы ячеек памяти связаны не только последовательностью
друг с другом, но и сумматорами в соответствии с
коэффициентами передачи a0, a1, …, an-1 A:
если ai=1, то значение Si(t) i-ой ячейки передается на
один из входов i-го сумматора;
если ai=0, то такая передача отсутствует.
Полагается a0 1.
Состояние LFSR в текущий момент времени t задается
двоичным n-вектор-столбцом S(t)=(Sn-1(t), …, S1(t), S0(t)).
34

35. LFSR

Содержание ячеек LFSR с течением времени изменяется
следующим образом, определяя тем самым динамику
состояний LFSR:
если i {0, 1, ..., n 2}
S i 1 (t ),
S i (t 1) n 1
a j S j (t ),
если i n 1
j 0
или в матричном виде:
a0 a1 a2 an 1
0
S (t 1) AS (t ), A
,
I n 1
0
где In-1 – единичная (n–1) (n–1)-матрица, t=0, 1, …
(11)
(12)
35

36. LFSR

Текущие значения нулевой ячейки регистра используются в
качестве элементов порождаемой LFSR двоичной
псевдослучайной последовательности St=S0(t) (см. рис.),
которая с учетом (11) удовлетворяет линейному
рекуррентному соотношению:
n 1
st n a j st j ,
t=0, 1, …
(13)
j 0
Модель (13) является частным случаем модели (6) линейной
рекурренты над полем F2, поэтому коэффициенты {aj}
выбираются согласно методике, приведенной в п.2.3 –
слайд 29.
36

37. Генератор Таусворта, основанный на LFSR

Генаратор Таусворта аналогичен (11-13) и определяется
следующими соотношениями:
A = (In + (L ) p) (In + L q),
(14)
S(t+1)=AS(t),
st=S0(t), t=0, 1, …,
где p, q – некоторые заданные натуральные числа (параметры
алгоритма); L – (n–1) (n–1)-двоичная матрица, все
единицы которой расположены лишь под главной
диагональю.
~
Преобразование S Lq S осуществляет сдвиг всех компонентов
вектора S «вниз» на q позиций, заполняя освободившиеся
позиции нулями.
~
Точно так же S ( L ) p S осуществляет сдвиг «вверх» на p
позиций.
37

38. Генератор Таусворта, основанный на LFSR

Выбор параметров p, q осуществляется таким образом, чтобы
матрица A имела порядок 2n –1 в группе невырожденных
n n-матриц.
При этом последовательность двоичных векторов {S(t)},
определяемых по (14), имеет максимально возможный
период Tmax = 2n – 1.
Это условие выполняется, например, если:
n=31, p=13, q=18 или p=18, q=13;
n=32, p=15, q=17 или p=17, q=15.
(15)
38

39. 3.5. Генераторы Фибоначчи

39

40.

Общий вид рекуррентного соотношения, определяющего
генератор Фибоначчи, задается уравнением
xt=xt–r xt–s, t=r, r+1, r+2, …,
(16)
где r, s N – параметры генератора; – символ бинарного
отношения: {+, –, , }.
В случае «+» или «–» {xt} – целые числа (mod 2k) для
некоторого заданного k N.
В случае « » {xt} – нечетные числа (mod 2k).
В случае « » элемент xt Vk представляет собой двоичный k–
вектор и действие выполняется покомпонентно.
Свойства псевдослучайной последовательности Фибоначчи
(16) и методика выбора параметров r, s, k излагаются в
доп. литературе.
40

41. 3.6. Криптостойкие генераторы на основе односторонних функций

41

42.

Для повышения стойкости алгоритмов генерации
псевдослучайных последовательностей к криптоанализу в
последнее время предлагается синтезировать алгоритмы
на основе известных в криптографии односторонних
функций.
Характерное свойство односторонних (one-way) функций
состоит в том, что для вычисления значения функции по
заданному значению аргумента существует
полиномиально-сложный алгоритм, в то время как для
вычисления аргумента по заданному значению функции
полиномиально-сложного алгоритма не существует (или
он не известен).
42

43.

Доказательство свойства односторонности функции является
трудной математической задачей.
Поэтому в криптосистемах часто используются «кандидаты в
односторонние функции», для которых показано лишь, что
в настоящее время не известны полиномиально-сложные
алгоритмы вычисления обратной функции.
Примерами таких кандидатов являются некоторые известные
криптоалгоритмы (например, DES) и хэш-функции
(например, SHA-1).
43

44. Генератор ANSI X9.17

Это национальный стандартный алгоритм США для генерации
двоичной псевдослучайной последовательности, входящей
в FIPS (USA Federal Information Processing Standard).
В этом генераторе в качестве кандидата односторонней
функции используется так называемый «тройной DES» с
двумя ключами K1, K2 V64 – это алгоритм шифрования
вида
FK E K1 DK 2 E K1
E
где K= (K1 || K2) V128 – составной 128-битовый ключ; K1 –
алгоритм шифрования DES с ключом K1; DK 2 – алгоритм
расшифрования DES с ключом K2 K1.
44

45. Генератор ANSI X9.17

Входными данными алгоритма ANSI X9.17 являются:
некоторое случайное (и конфиденциальное) 64-битовое
стартовое число s V64;
128-битовый составной ключ K V128;
m – количество 64-битовых двоичных слов, которые
необходимо получить на выходе генератора.
Выходными данными являются m 64-битовых двоичных слов
x1, x2, …, xm V64.
45

46. Алгоритм генерации ANSI X9.17

Шаг 1. Фиксируется 64-битовое представление d V64 даты и
времени при обращении к программе генерации и
вычисляется вспомогательное 64-битовое двоичное слово
I = FK(d).
Шаг 2. Для i=1, 2, …, m повторяются шаги 3, 4.
Шаг 3. Вычисляется значение i-го выходного слова:
xi= FK(I s).
Шаг 4. Вычисляется новое значение параметра s:
s = FK(xi I).
Шаг 5. Формируется выходная последовательность m слов x1,
x2, …, xm V64, либо двоичная последовательность из 64m
битов:
X=(x1 || x2 || … || xm) V64m.
46

47. 3.7. Криптостойкие генераторы, основанные на проблемах теории чисел

47

48.

Стойкость генераторов псевдослучайных последовательностей,
рассматриваемых в данном параграфе, основывается на
неразрешимости с полиномиальной сложностью (на
данный момент) некоторых известных проблем теории
чисел:
факторизации больших чисел
и дискретного логарифмирования.
48

49. RSA-алгоритм генерации псевдослучайных последовательностей

Этот алгоритм основывается на том факте, что в настоящее
время криптоанализ RSA не может быть осуществлен с
полиномиальной сложностью.
RSA-алгоритм генерации двоичной псевдослучайной
последовательности x1, x2, …, xn A состоит из шести
шагов.
49

50. RSA-алгоритм генерации псевдослучайных последовательностей

Шаг 1. Как и в RSA-криптосистеме, генерируются достаточно
большие различные простые числа p, q и вычисляются
числа N=pq, =(p-1)(q-1). Выбирается случайное целое
число k, 1<k< , взаимно простое с , так, что НОД(k, )=1.
Шаг 2. Выбрать случайное целое – стартовое значение – u0
{1, 2, …, N – 1}.
Шаг 3. Для i=1, 2, …, n повторяются шаги 4, 5.
Шаг 4. Вычислить ui= ui-1k mod N {0, 1, …, N – 1}.
Шаг 5. Вычислить xi A={0, 1} – самый младший бит числа ui
в двоичном представлении.
Шаг 6. Сформировать выходную последовательность x1, x2, …,
xn .
50

51. RSA-алгоритм генерации псевдослучайных последовательностей

Недостатком RSA-алгоритма является его невысокое
быстродействие при реализации на универсальных
компьютерах, вызванное большими затратами машинного
времени при выполнении модулярного умножения на шаге
4.
Для повышения быстродействия на шаге 5 можно выделять
сразу несколько младших битов. Эта идея используется в
модификации Микали-Шнорра RSA-алгоритма.
51

52. 3.8. Методы улучшения элементарных псевдослучайных последовательностей

52

53.

Пусть 1, 2, … A – некоторая двоичная псевдослучайная
последовательность, сгенерированная одним из
простейших методов и называемая (в данном параграфе)
элементарной.
Чтобы построить псевдослучайную последовательность со
свойствами, более близкими к свойствам РРСП, чем
элементарная последовательность, осуществим
функциональное преобразование { i}:
x1 = f1( 1, 2, …), x2 = f2( 1, 2, …), …,
(17)
где f1( ), f2( ), … – некоторые функционалы, задающие
отображение A A.
53

54.

Функционалы f1( ), f2( ), … следует подбирать так, чтобы
преобразованная последовательность {xk} имела
вероятностное распределение, более близкое к
распределению РРСП, чем распределение { i}.
Выбирая различные функционалы f1( ), f2( ), … и метрики в
пространстве вероятностных распределений, можно
разработать множество методов и алгоритмов
«улучшения» элементарных псевдослучайных
последовательностей.
54

55. 3.9. Комбинирование алгоритмов генерации методом Макларена-Марсальи

3.9. Комбинирование алгоритмов
генерации методом МакларенаМарсальи
55

56.

Пусть имеется два простейших генератора псевдослучайных
последовательностей: G1 и G2.
Генератор G1 порождает элементарную последовательность над
алфавитом мощности N:
x0, x1, x2, …, A(N), A={0, 1, …, N-1},
а генератор G2 - над алфавитом мощности K:
y0, y1, y2, …, A(K), A={0, 1, …, K-1}.
Пусть имеется вспомогательная таблица
T={T(0), T(1), …, T(K-1)}
из K целых чисел (память из K ячеек).
56

57. Метод Макларена-Марсальи

Метод Макларена-Марсальи комбинирования
последовательностей {xi}, {yi} для получения выходной
псевдослучайной последовательности {zk} состоит в
следующем.
Сначала T-таблица заполняется K первыми членами
последовательности {xi}:
T(i) xi , i=0, 1, …, K-1.
Элементы выходной последовательности вычисляются
следующим образом:
s yk , zk= T(s), T(s)= xK+k , k=0, 1, ...
Т.о., генератор G2 осуществляет случайный выбор из Tтаблицы, п также ее «случайное» заполнение
«случайными» числами, порождаемыми генератором G1.
Метод комбинирования Макларена-Марсальи позволяет
ослабить зависимость между членами {zk} и увеличить
период псевдослучайной последовательности.
57