Similar presentations:
Основное свойство алгебраической дроби
1.
07.04.20251
2.
Повторить основное свойство дроби ирассмотреть это свойство для алгебраических
дробей;
Научиться сокращать и приводить дроби к
наименьшему общему знаменателю.
07.04.2025
2
3.
Понятие основного свойства дроби известно изкурса 5-го класса (сокращение дробей).
Значение обыкновенной дроби не изменится, если ее
числитель и знаменатель одновременно умножить или
разделить на одно и то же отличное от нуля число.
Например:
3 12 (числитель и знаменатель мы одновременно
умножили на одно и то же число 4, значение
4 16 дроби не изменилось);
22 2 (числитель и знаменатель мы одновременно
разделили на одно и то же число 11, значение
33 3 дроби не изменилось).
07.04.2025
3
4.
Над алгебраическими дробями можно осуществлятьпреобразования аналогичные тем, которые указали
для обыкновенной дроби.
Основное свойство алгебраической дроби:
1. И числитель и знаменатель алгебраической дроби можно
умножить на один и тот же многочлен, на одно и тоже,
отличное от нуля число ( тождественное преобразование
алгебраической дроби).
2. И числитель и знаменатель алгебраической дроби можно
разделить на один и тот же многочлен, на одно и тоже,
отличное от нуля число ( тождественное преобразование
алгебраической дроби – сокращение алгебраической дроби).
07.04.2025
4
5.
a a;
b b
a
a
;
b
b
a
a
;
b a
a b
a
a
;
a b
a b
a b (b a )
b a
;
c d
c d
c d
a b
(a b)
a b
.
c d (d c )
d c
(a b) (b a ) ;
2
07.04.2025
2
5
6.
Как используют основное свойство алгебраической дроби?Пример 1:
Преобразовать данные дроби так, чтобы получились дроби
с одинаковыми знаменателями.
2a 3b
и
3 5
Решение
Для этого найдем дополнительные множители для
каждой дроби. Это числа 5 и 3.
2a 2a 5 10 a 5 – дополнительный множитель
;
3
3 5
15
3b 3b 3 9 b
;
5
5 3 15
3 – дополнительный множитель
6
07.04.2025
7.
Пример 2:Преобразовать данные дроби так, чтобы получились дроби
с одинаковыми знаменателями.
a
a2
и 3
2
4b 6 b
Решение
Для этого найдем дополнительные множители для
каждой дроби. Это числа 3b и 2.
a
a 3b
3ab
2
; 3b – дополнительный множитель
2
3
4b
4 b 3b 12b
a
a 2
2a
3
; 2 – дополнительный множитель
3
3
6b
6 b 2 12b
07.04.2025
7
8.
Пример3:Преобразовать данные дроби так, чтобы получились дроби
с одинаковыми знаменателями.
x
x
и
x y x y
Решение
Для этого найдем дополнительные множители для
каждой дроби. Это многочлены - (x - y) и (x + y).
x
x ( x y )
x 2 xy (x - y) – дополнительный
2 2 ;множитель
x y ( x y )( x y ) x y
x
x ( x y )
x 2 xy (x + y) – дополнительный
2 2 ;
множитель
x y ( x y )( x y ) x y
07.04.2025
8
9.
Пример 4:Преобразуйте заданные тройки алгебраических выражений так,
чтобы получились дроби с одинаковыми знаменателями:
( x 1 )( x 1 )
х 1
x 1
;
2 х 2 2( x 1 ) 2( x 1 )( x 1 )
2
2
2
х
х
х
;
2
2
2 х 2 2( х 1 ) 2( x 1 )( x 1 )
2 х 3 2( 2 x 3 )( x 1 )
;
2( x 1 )( x 1 )
х 1
07.04.2025
9
10.
Пример 5:Преобразуйте заданные тройки алгебраических выражений так,
чтобы получились дроби с одинаковыми знаменателями:
1
1
2 y( y 2 )
;
y 2
2 y
( y 2 )( y 2 ) 2 y
2 y( y 2 )
1
;
2 y( y 2 )( y 2 )
2 y
y 4
y 4
y 4
.
2
3
2 y 8 y 2 y( y 4 ) 2 y( y 2 )( y 2 )
2
07.04.2025
2
2
10
11.
Сократите данные дроби:1
1
1
2
12 а b x 6 2 a a b x 2a x
а)
;
2 2
2
2
18 a b y
6 3 a b y
3y
4
2
1
2
2
2
1
1
1
3x y 6 x y
3 x y( 1 2 y ) ( 1 2 y )
б) 3
2
.
2 2
3 x y 12 x y
3 x y( x 4 y ) ( x 4 y )
2
2
2
2
1
07.04.2025
11
12.
Сократите дробь:4 а х 4 ах
в) 3
2 2
3
6 а х 12а х 6 ах
3
3
4 ах( a х )
2
2
6 ах( a 2ах х )
2
2
4 ах ( a х )( a x )
2
6
ах
(
a
х
)
1
1
1
2 2 ах( a х )( a x ) 2( a x )
.
3( a x )
21 3 ах
(
a
х
)(
a
x
)
1
1
07.04.2025
12
13.
Назовите основное свойствоалгебраической дроби;
Как изменяются знаки у числителя
и
знаменателя алгебраической дроби
(следствие из основного свойства
дроби)?
07.04.2025
13










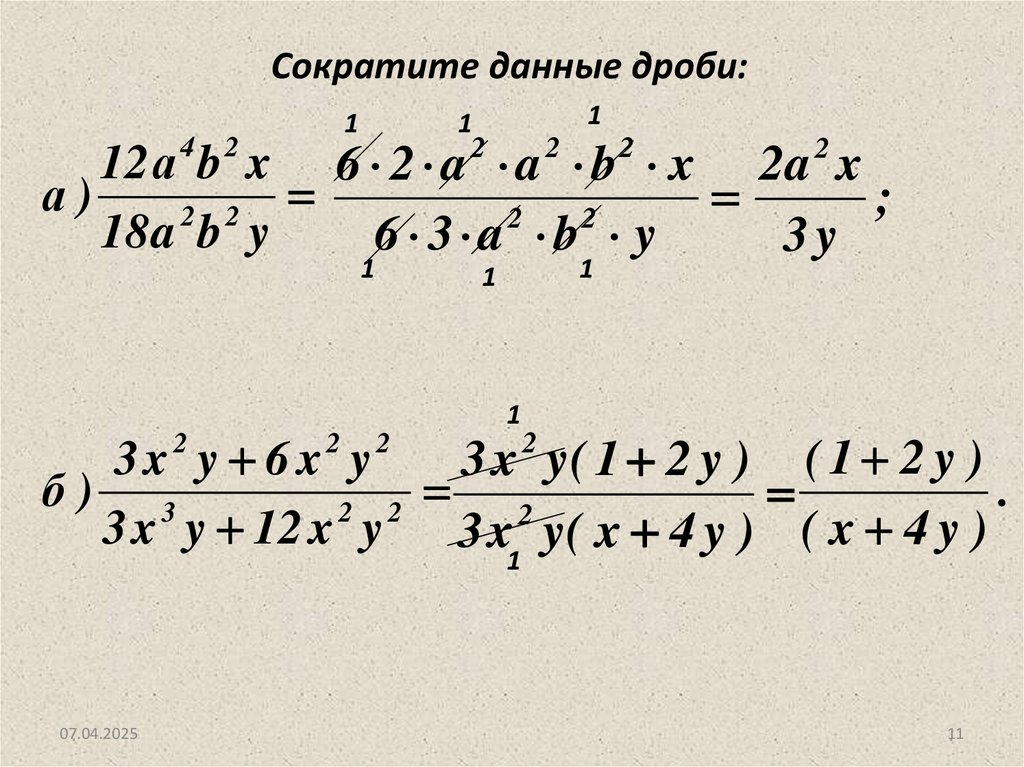
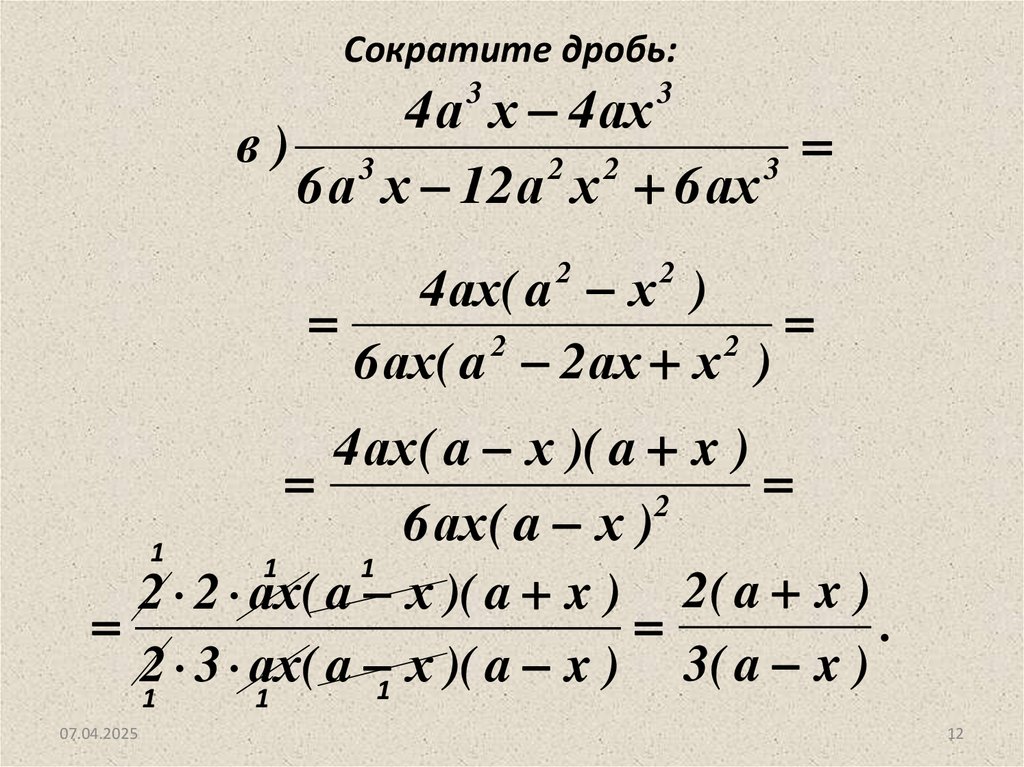

 mathematics
mathematics