Биномиальная куча. Пирамидальная сортировка. Методы программирования

1.

Методы программирования, 6 семестр
Якимова О.П.

2.

Терминология
Пирамида
Куча
Очередь с приоритетами
Многозначность понятий
Куча: бинарное дерево и способ организации памяти
Очередь с приоритетами: структура данных или задача

3.

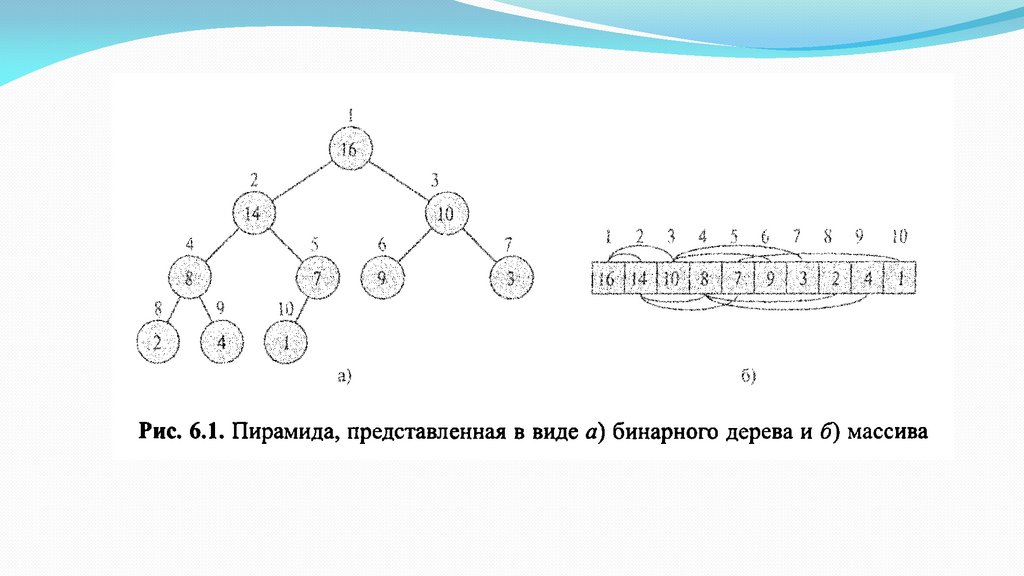
Пирамида (бинарная куча binary heap) — это структура данных,
представляющая собой объект-массив, который можно
рассматривать как почти полное бинарное дерево
Каждый узел этого дерева соответствует определенному элементу
массива. На всех уровнях, кроме, может быть, последнего,
дерево полностью заполнено (заполненный уровень — это
такой, который содержит максимально возможное количество
узлов). Последний уровень заполняется слева направо до тех
пор, пока в массиве не закончатся элементы.

4.

5.

Пирамида(двоичная куча) – это структура данных на основе
бинарного дерева, обладающая следующими свойствами:
минимальный(максимальный) элемент находится в корне
(элементе массива с индексом 0);
любой элемент кучи не больше своих детей;
дети находятся в элементах с индексами 2i+1 и 2i+2.
Операции:
добавить элемент в кучу;
получить минимальный(максимальный);
удалить элемент из кучи.

6.

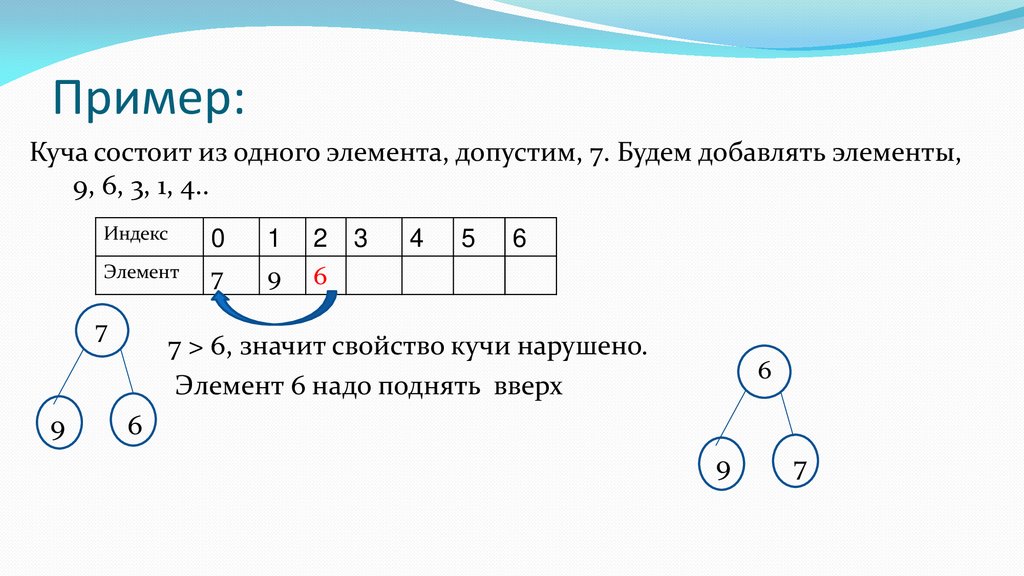
Пример:
Куча состоит из одного элемента, допустим, 7. Будем добавлять элементы,
9, 6, 3, 1, 4..
Индекс
Элемент
7
9
0
7
1
9
2
6
3
4
5
6
7 > 6, значит свойство кучи нарушено.
Элемент 6 надо поднять вверх
6
6
9
7

7.

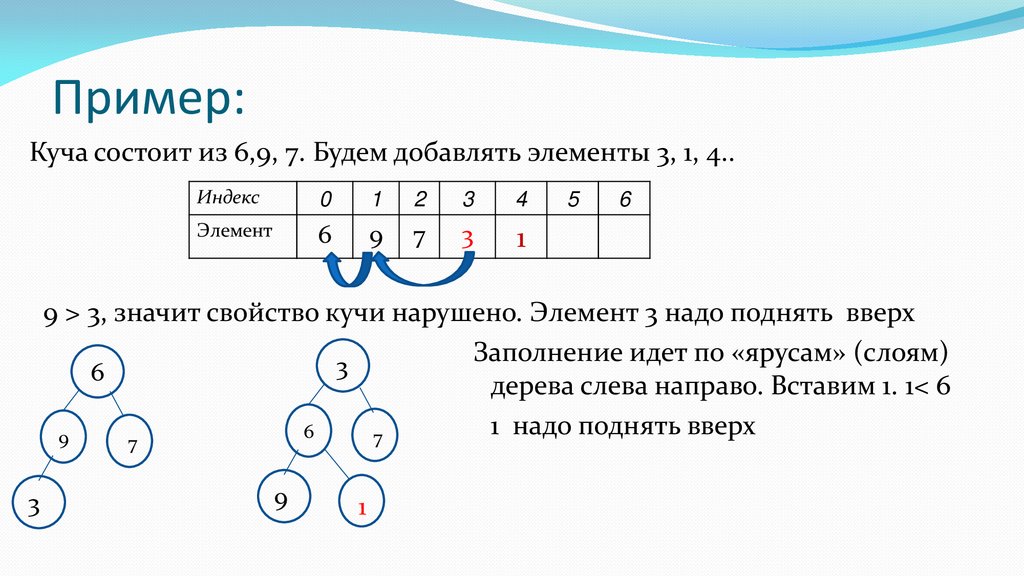
Пример:
Куча состоит из 6,9, 7. Будем добавлять элементы 3, 1, 4..
Индекс
0
1
2
3
4
Элемент
6
9
7
3
1
5
6
9 > 3, значит свойство кучи нарушено. Элемент 3 надо поднять вверх
Заполнение идет по «ярусам» (слоям)
3
6
дерева слева направо. Вставим 1. 1< 6
1 надо поднять вверх
6
7
9
7
3
9
1

8.

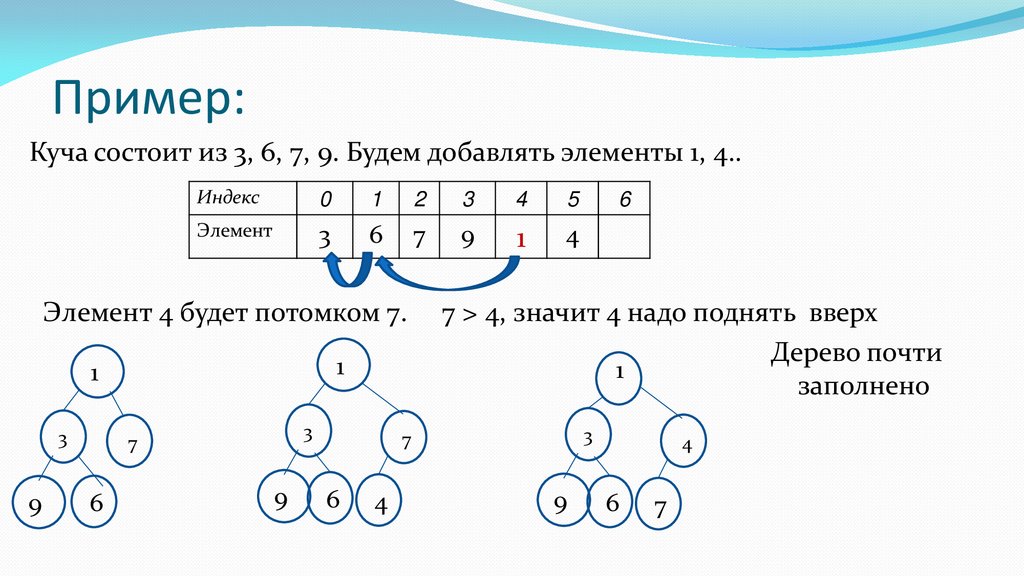
Пример:
Куча состоит из 3, 6, 7, 9. Будем добавлять элементы 1, 4..
Индекс
0
1
2
3
4
5
Элемент
3
6
7
9
1
4
Элемент 4 будет потомком 7.
1
1
3
9
3
7
6
9
7 > 4, значит 4 надо поднять вверх
Дерево почти
1
заполнено
3
7
6
4
6
9
4
6
7

9.

Виды куч(пирамид)
Невозрастающая пирамида:
A[parent[i]] >= A[i], т.е. в корне максимальный элемент
Неубывающая пирамида:
A[parent[i]] <= A[i], т.е. в корне минимальный элемент

10.

Вопросы
Чему равно минимальное и максимальное количество элементов в
пирамиде высотой h?
Где в невозрастающей пирамиде может находиться наименьший ее
элемент, если все элементы различаются по величине?
Является ли массив с отсортированными элементами неубывающей
пирамидой?
Является ли последовательность {23,17,14,6,13,10,1,5,7,12}
невозрастающей пирамидой?
https://learningapps.org/10307447

11.

Восстановление свойства пирамиды
В примере мы рассматривали неубывающую пирамиду, но для целей
сортировки нам будет нужна невозрастающая пирамида – т.е. в
корне - максимальный элемент.
В процессе работы с этой структурой данных нам потребуется
процедура Heapify. На ее вход подается массив А и индекс i
элемента этого массива.
При вызове процедуры Heapify предполагается, что A[i] < своих детей
и это надо исправить. Место iго элемента займет бОльший из его
детей, а iй спустится ниже.

12.

public void Heapify(int index)
{
var left = 2 * index + 1;
var right = 2 * index + 2;
var largest = index;
if (left < HeapSize && _comparer.Compare ( Heap [left], Heap[index])>0)
{
largest = left; }
if (right < HeapSize && _comparer.Compare(Heap[right ], Heap[largest]) > 0)
{
largest = right; }
if (largest == index) return;
var temp = Heap[largest];
Heap[largest] = Heap[index];
Heap[index] = temp;
Heapify(largest);
}

13.

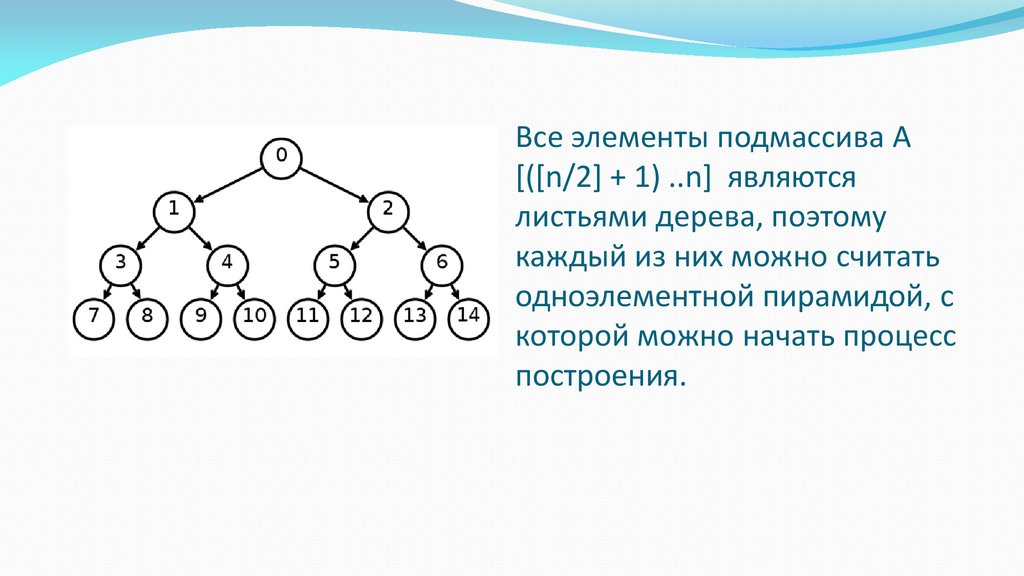
Создание пирамиды

14.

Все элементы подмассива А
[([n/2] + 1) ..n] являются
листьями дерева, поэтому
каждый из них можно считать
одноэлементной пирамидой, с
которой можно начать процесс
построения.

15.

Создание пирамиды
С помощью процедуры Heapify можно преобразовать массив А[1..n],
в невозрастающую пирамиду в направлении снизу вверх.
Процедура BuildMaxHeap проходит по остальным узлам и для каждого
из них выполняет процедуру Heapify:
for (var i = (HeapSize-1) / 2; i >= 0; i--)
{
Heapify(i);
}

16.

Задание
1. Выполните Heapify(2) с массивом
А = {27,17,3,16,13,10,1,5,7,12,4,8,9,0}.
2. Дан массив A = { 5,3,17,10,84,19,6, 22, 9 } . Постройте из этого
массива бинарную кучу.

17.

Алгоритм пирамидальной сортировки
1. Из массива получаем невозрастающую пирамиду. Максимальный
элемент в корне.
2. Меняем элемент из корня(с индексом ноль) с элементом стоящем на
последнем месте. Теперь максимальный стоит на своем месте –
последним.
3. Уменьшаем размер кучи на 1. Восстанавливаем ее свойства, спуская
элемент из корня на положенное место.
Повторяем шаги 2 и 3, пока размер кучи не станет 0.

18.

Сортировка кучей на месте

19.

20.

21.

Спасибо за внимание!