Измерение связи между явлениями. Методы изучения корреляционных связей при оценке показателей здоровья

1. ИЗМЕРЕНИЕ СВЯЗИ МЕЖДУ ЯВЛЕНИЯМИ. МЕТОДЫ ИЗУЧЕНИЯ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ ПРИ ОЦЕНКЕ ПОКАЗАТЕЛЕЙ ЗДОРОВЬЯ И ФАКТОРОВ ОКРУЖАЮЩЕЙ

Практическое занятие № 5.

2.

—
понятие,
взаимосвязь между признаками.
которое
означает
Различают две формы проявления количественных
связей
между
явлениями
или
процессами:
функциональную и корреляционную.

3.

Под
понимают такую связь, при
которой любому значению одного из признаков
соответствует строго определенное значение другого
(радиусу круга соответствует определенная площадь
круга, скорость свободно падающего тела определяется
величиной ускорения силы тяжести и времени падения).
Функциональная связь характерна для физикохимических процессов.

4.

В социально-гигиенических исследованиях, а также в
клинической медицине и биологии зависимости между явлениями
носят иной характер — характер корреляционной связи.
Корреляционная связь – это связь, при которой
каждому определенному
значению одного признака
соответствует несколько значений другого взаимосвязанного
с ним признака.
Всем известно, что рост и масса тела человека связаны между собой. У
группы лиц с одинаковым ростом наблюдаются различные колебания массы
тела. Однако эти колебания массы тела варьируют в определенных размерах —
вокруг своей средней величины.
Корреляционная связь необходима, например, при оценке
взаимосвязей между стажем работы и уровнем заболеваемости
работающих; между разными уровнями физических факторов
окружающей среды и состоянием здоровья; между сроками
госпитализации и частотой осложнений.

5.

Корреляция может быть представлена в
виде таблицы, графика и коэффициента
корреляции. Таблицы и графики дают
представление о наличии и направлении связи.
Так, между температурой воздуха и числом
случаев бронхита существует корреляционная
связь. Однако измерить и оценить
статистическую достоверность этой связи
можно лишь при помощи специального
коэффициента корреляции (rxy) и его средней
ошибки (mr).

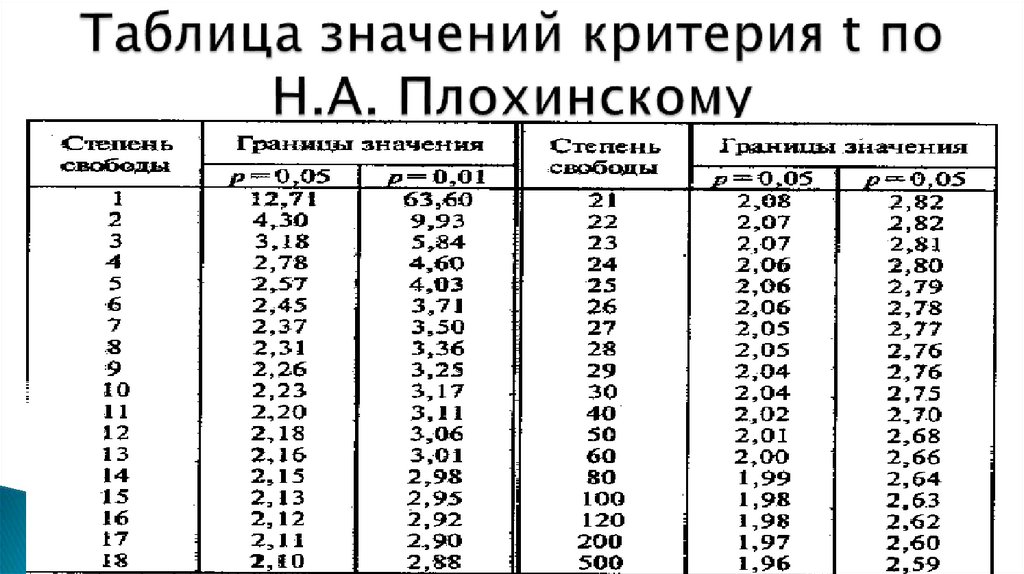
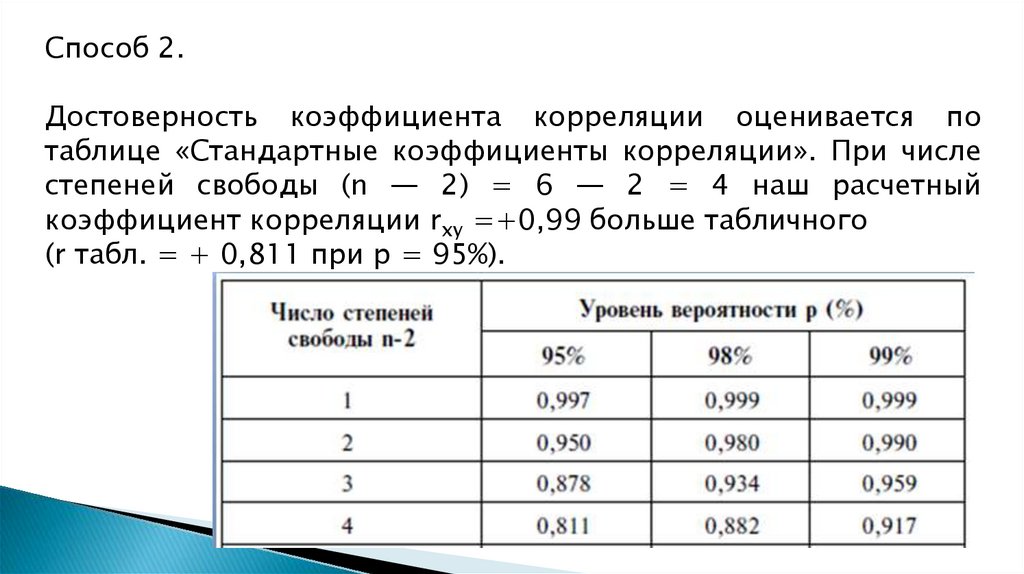
6. Методы определения коэффициента корреляции

Критерий корреляции – это метод параметрической статистики, позволяющий
определить наличие или отсутствие линейной корреляции (связи) между двумя
количественными показателями, а также оценить ее тесноту и статистическую значимость.
Коэффициент корреляции находит широкое применение в работе врача любой специальности.
Например, врач-педиатр использует этот показатель при оценке физического развития детей и подростков,
социальный гигиенист — для определения зависимости между конкретными условиями труда и быта и состоянием
здоровья обследуемых контингентов.
Коэффициент корреляции позволяет определить зависимость частоты случаев
заболеваний у обследуемых контингентов от их возраста, стажа работы, наличия какихлибо производственных вредностей (уровень концентрации токсических веществ), а
также установить, в какой из изучаемых групп эта зависимость выражена сильнее.
Определяется по методам:
метод квадратов (метод Пирсона);
ранговый метод (метод Спирмена).

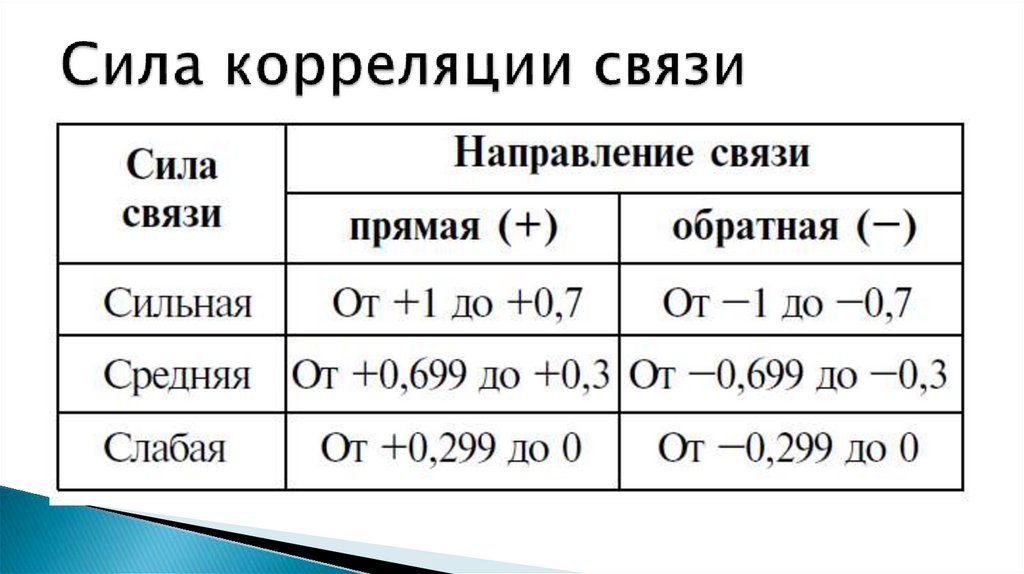
7. Сила связи и направление

Коэффициент корреляции (rxy) одним
числом измеряет силу связи между
изучаемыми явлениями и дает представление
о ее направлении.

8. Направление корреляции связи

Корреляционная связь бывает:
1.
прямой;
2.
обратной.
При прямой связи с увеличением значений одного признака
возрастает среднее значение другого признака. Например, с
повышением температуры тела увеличивается частота пульса у
большинства инфекционных больных; с увеличением роста
ребенка увеличивается масса его тела. Коэффициент корреляции,
характеризующий прямую связь, обозначается знаком плюс (+).
При обратной связи с увеличением одного признака
убывает среднее значение другого признака. Например, чем ниже
температура воздуха в осенний период, тем выше заболеваемость
детей острым бронхитом. Коэффициент корреляции,
характеризующий обратную связь, обозначается знаком минус (-).

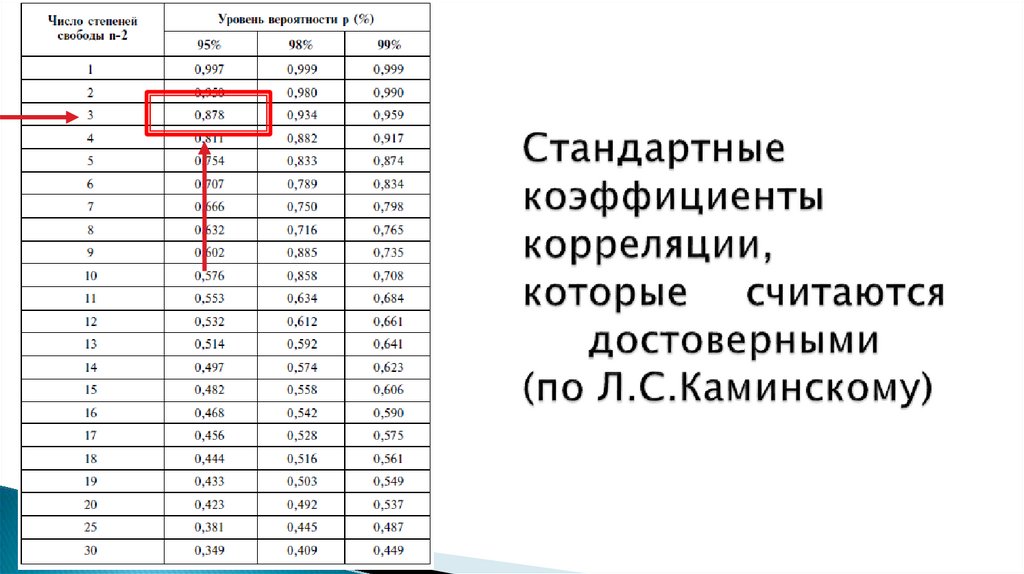
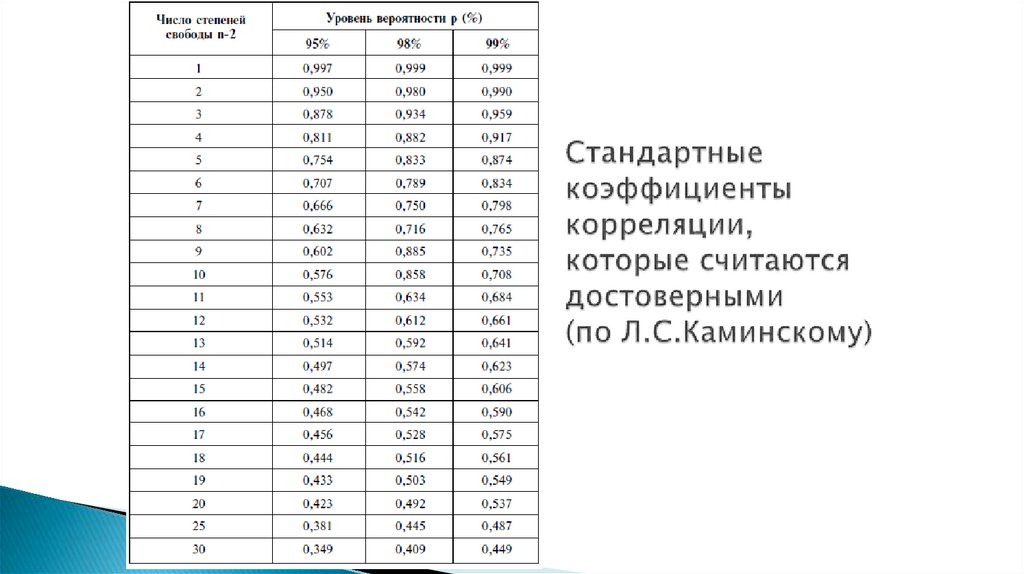
9. Сила корреляции связи

10. Рекомендации по применению метода ранговой корреляции (метод Спирмена)

Когда
нет
необходимости
в
точном
установлении
силы
связи,
а
достаточно
ориентировочных данных;
Когда
признаки представлены не только
количественными,
но
и
атрибутивными
значениями;
Когда ряды распределения признаков имеют
открытые варианты (например, стаж работы до
1 года и др.)

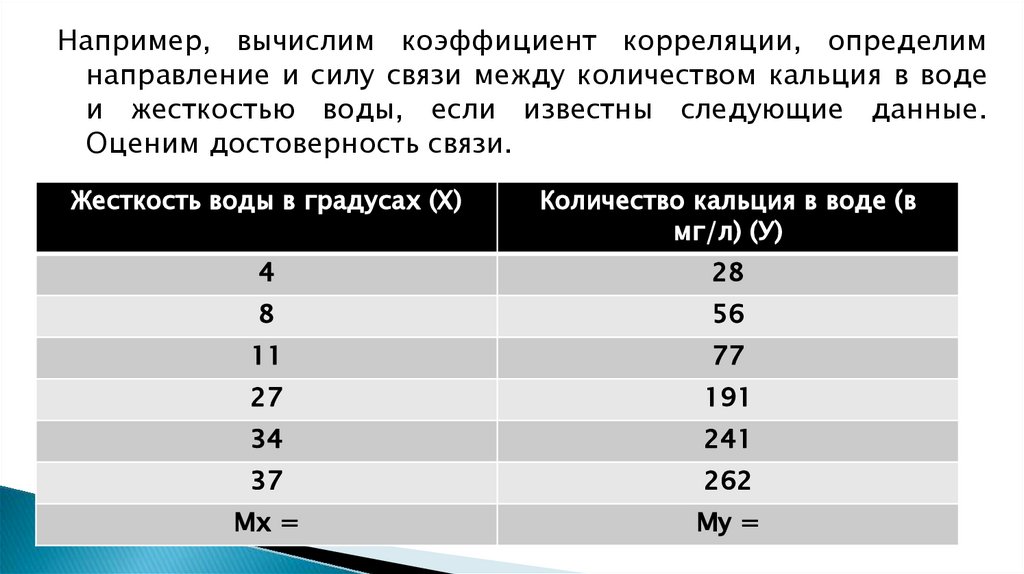
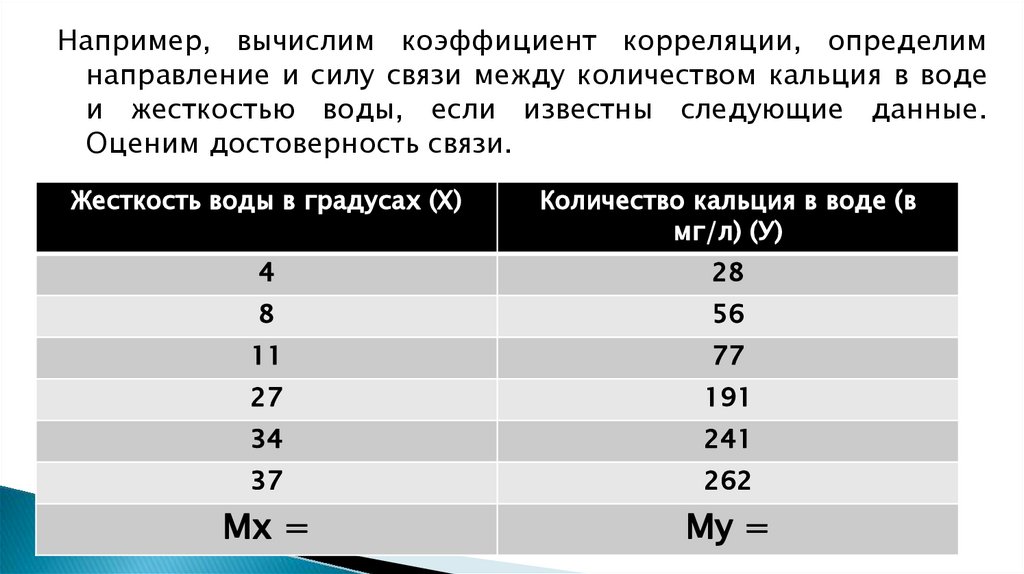
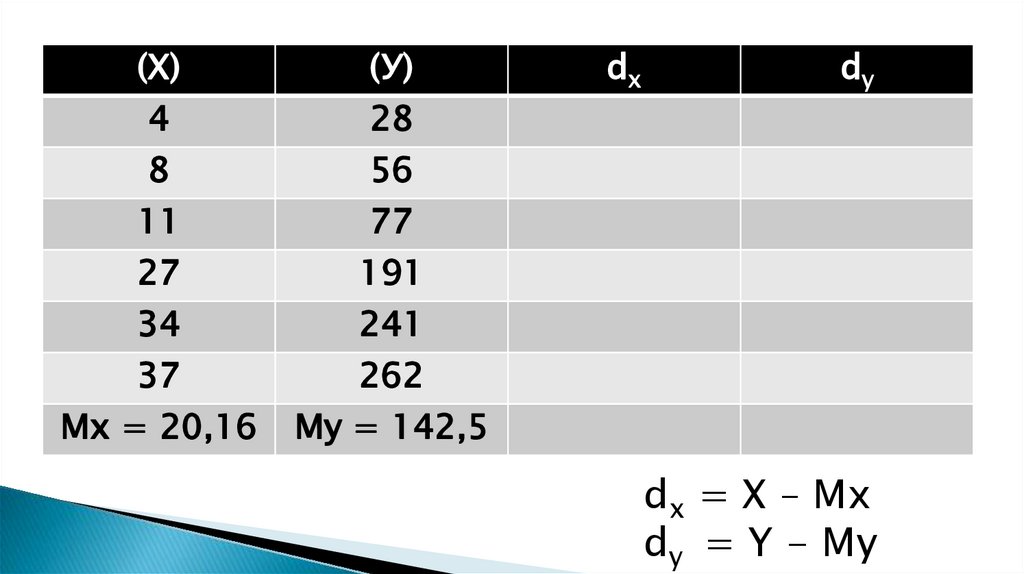
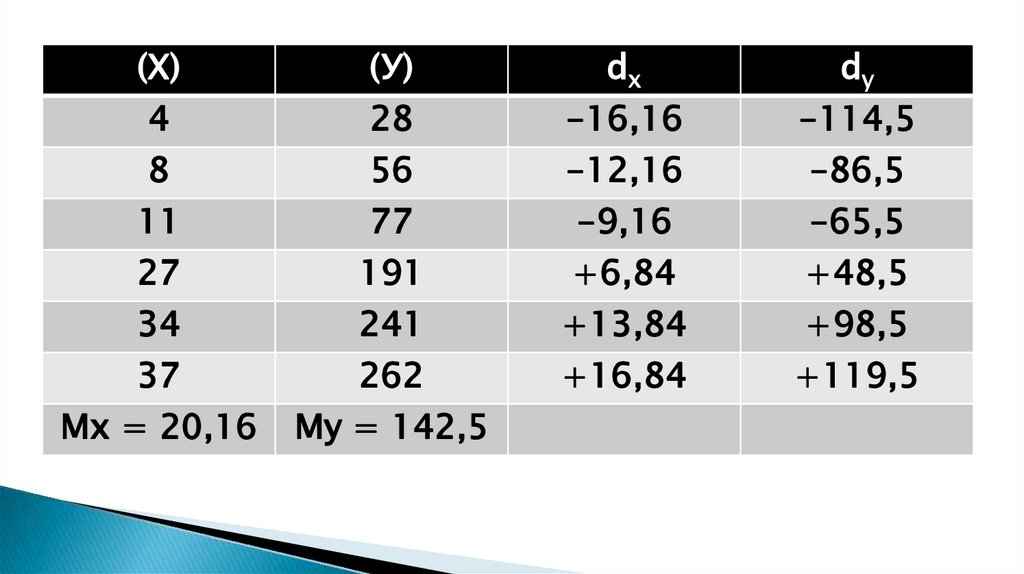
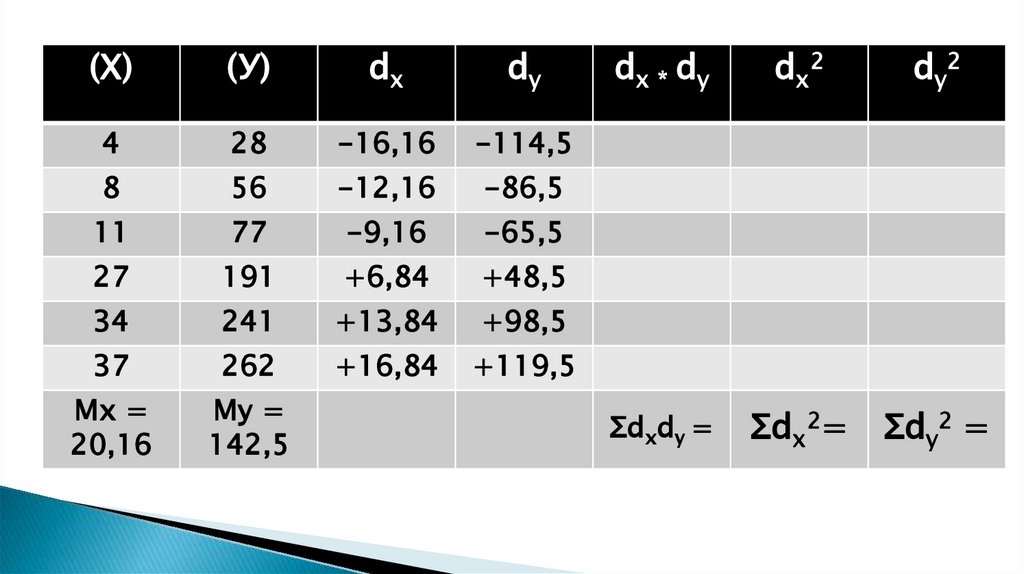
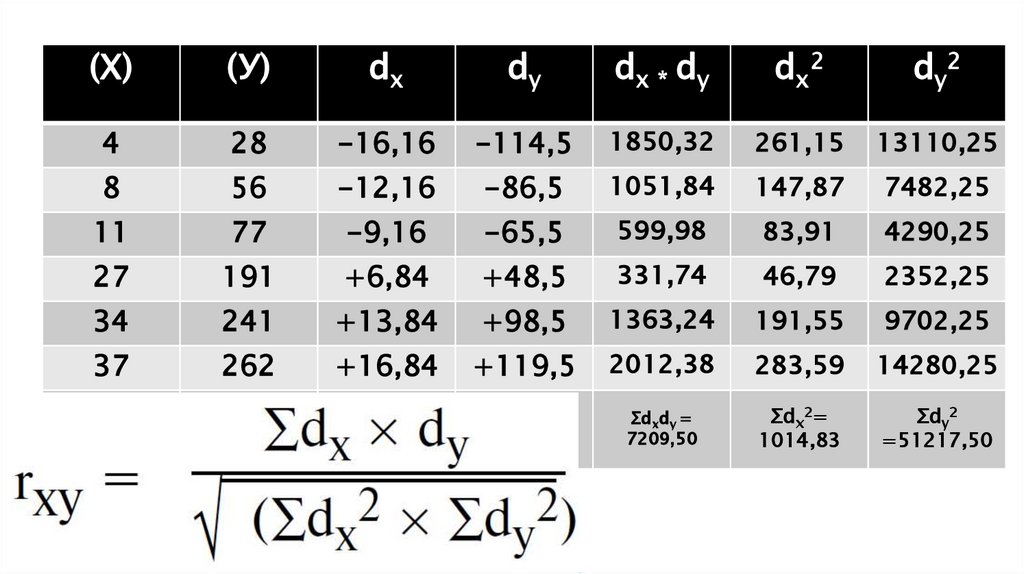
11. Методика и порядок вычисления коэффициента корреляции

Составить два ряда из парных сопоставляемых признаков, обозначив
первый и второй ряд соответственно х и у;
Величину признака в каждом из сравниваемых рядов заменить
порядковым номером (рангом);
Определить разность рангов между х и у (d): d = х — у;
Возвести полученную разность рангов в квадрат (d2);
Получить сумму квадратов разности (Σ d2) и подставить полученные
значения в формулу:

12.

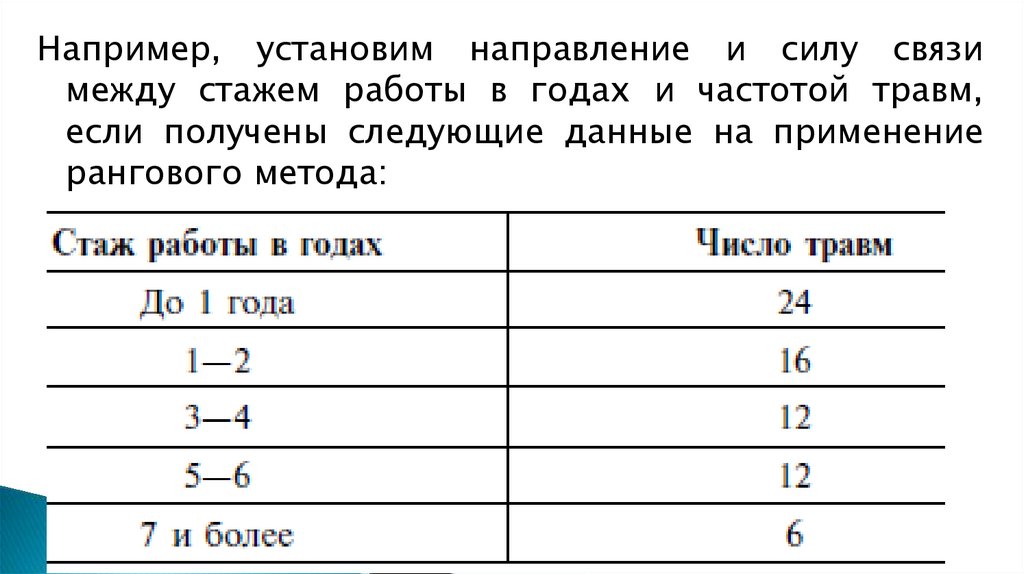
Например, установим направление и силу связи
между стажем работы в годах и частотой травм,
если получены следующие данные на применение
рангового метода:

13.

Например, установим направление и силу связи между стажем работы
в годах и частотой травм, если получены следующие данные на
применение рангового метода:
Стаж работы в
годах
Число травм
Порядковые номера (ранги)
Х
До 1 года
24
1–2г
16
3–4г
12
5–6л
12
7 и более
6
У

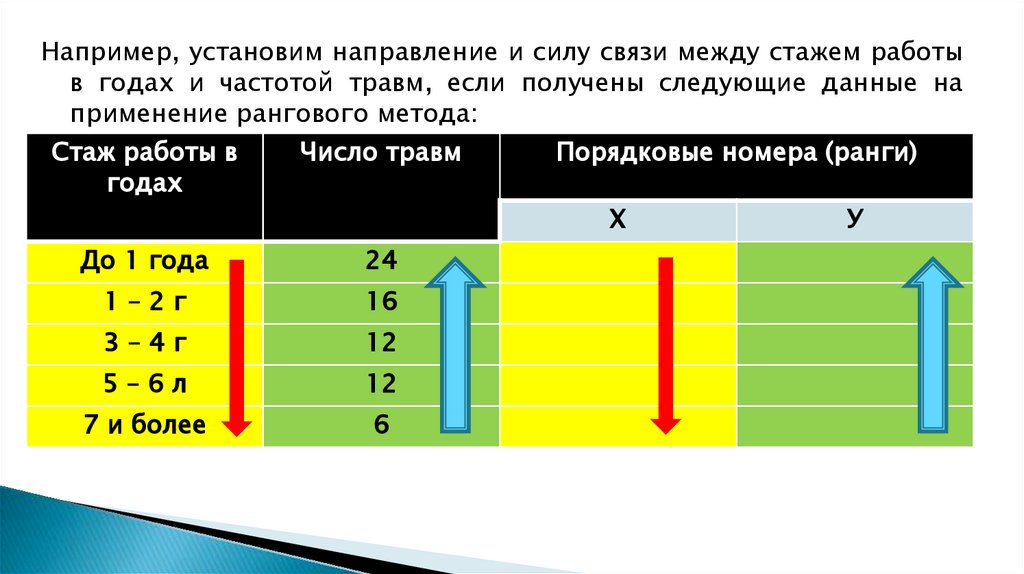
14.

Например, установим направление и силу связи между стажем работы
в годах и частотой травм, если получены следующие данные на
применение рангового метода:
Стаж работы в
годах
Число травм
Порядковые номера (ранги)
Х
У
До 1 года
24
1
5
1–2г
16
2
4
3–4г
12
3
2,5
5–6л
12
4
2,5
7 и более
6
5
1

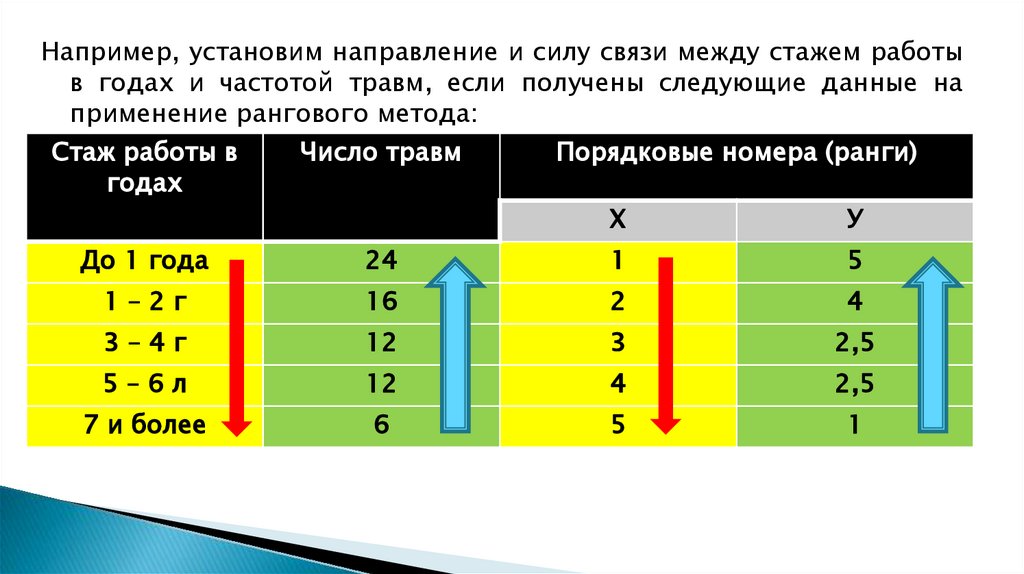
15.

Например, установим направление и силу связи между стажем работы
в годах и частотой травм, если получены следующие данные на
применение рангового метода:
Стаж работы Число травм
в годах
Порядковые номера
(ранги)
Х
У
До 1 года
24
1
5
1–2г
16
2
4
3–4г
12
3
2,5
5–6л
12
4
2,5
7 и более
6
5
1
Разность
рангов (d)
Х-У

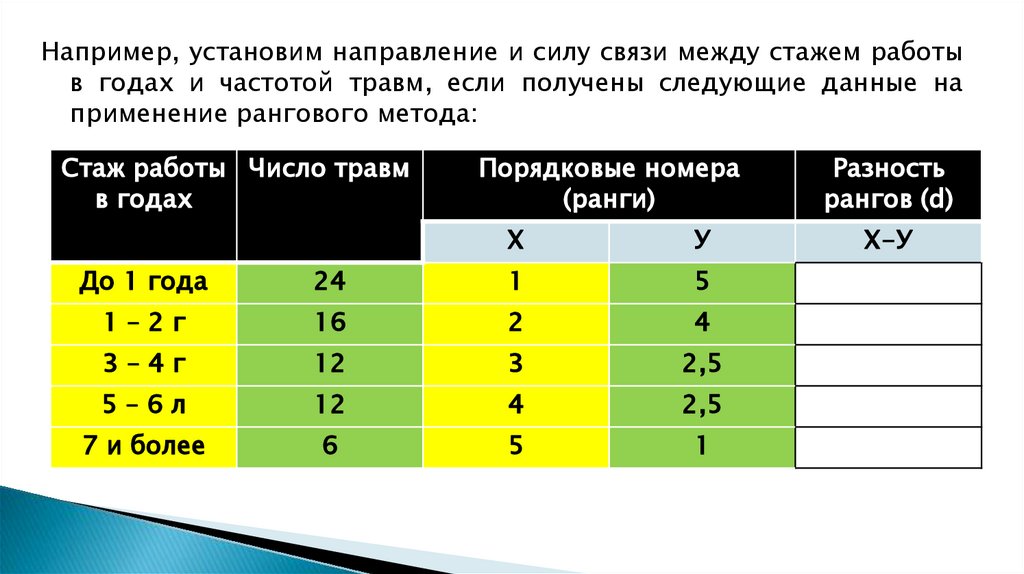
16.

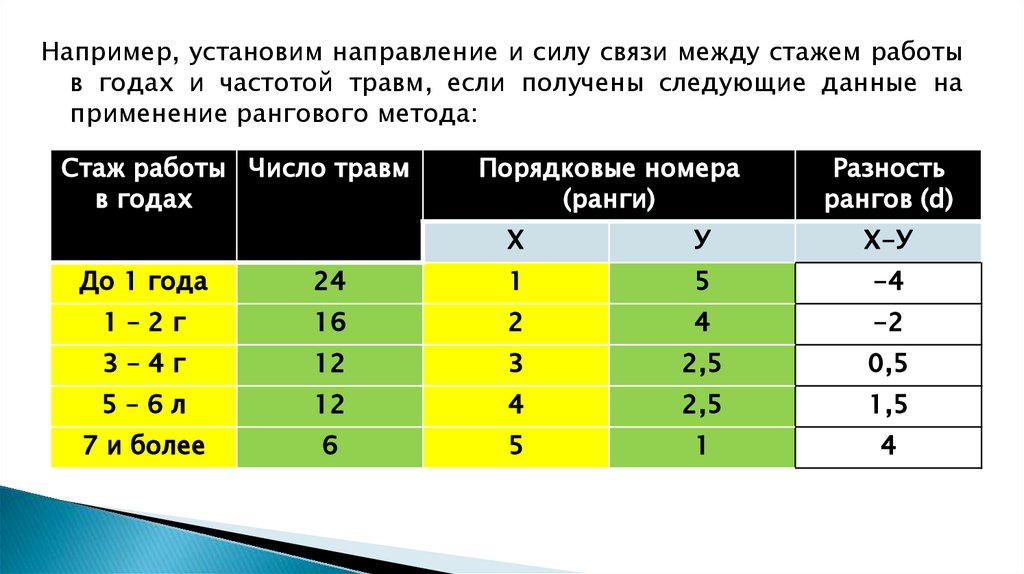
Например, установим направление и силу связи между стажем работы
в годах и частотой травм, если получены следующие данные на
применение рангового метода:
Стаж работы Число травм
в годах
Порядковые номера
(ранги)
Разность
рангов (d)
Х
У
Х-У
До 1 года
24
1
5
-4
1–2г
16
2
4
-2
3–4г
12
3
2,5
0,5
5–6л
12
4
2,5
1,5
7 и более
6
5
1
4

17.

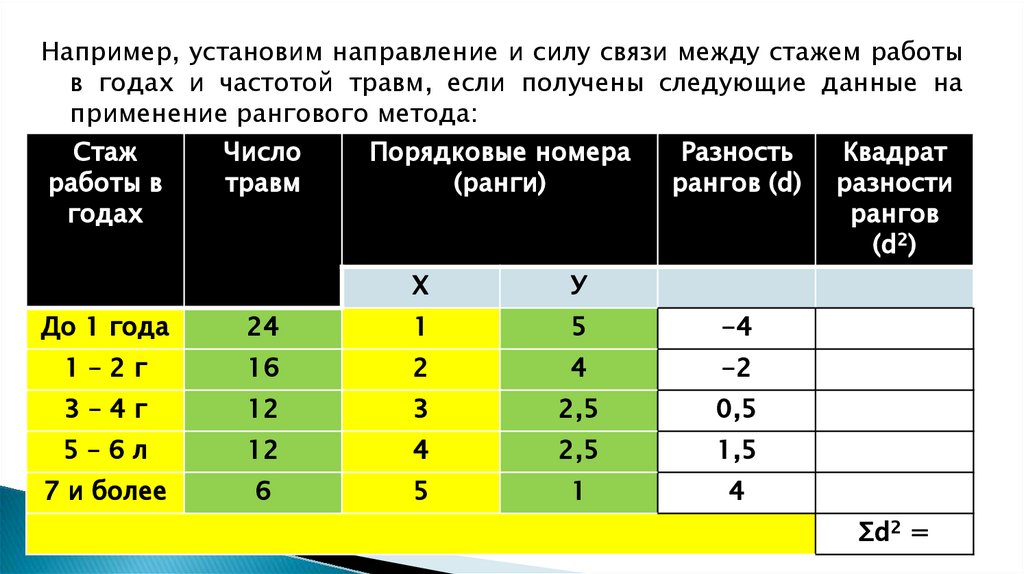
Например, установим направление и силу связи между стажем работы
в годах и частотой травм, если получены следующие данные на
применение рангового метода:
Стаж
работы в
годах
Число
травм
Порядковые номера
(ранги)
Х
У
Разность
рангов (d)
До 1 года
24
1
5
-4
1–2г
16
2
4
-2
3–4г
12
3
2,5
0,5
5–6л
12
4
2,5
1,5
7 и более
6
5
1
4
Квадрат
разности
рангов
(d2)
Σd2 =

18.

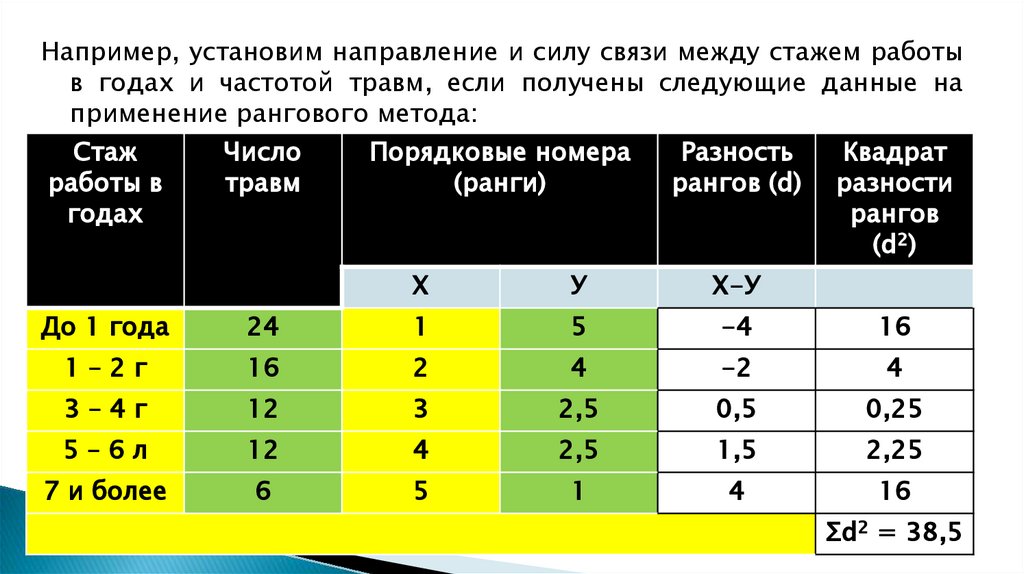
Например, установим направление и силу связи между стажем работы
в годах и частотой травм, если получены следующие данные на
применение рангового метода:
Стаж
работы в
годах
Число
травм
Порядковые номера
(ранги)
Разность
рангов (d)
Х
У
Х-У
Квадрат
разности
рангов
(d2)
До 1 года
24
1
5
-4
16
1–2г
16
2
4
-2
4
3–4г
12
3
2,5
0,5
0,25
5–6л
12
4
2,5
1,5
2,25
7 и более
6
5
1
4
16
Σd2 = 38,5

19.

Произвести
расчет
коэффициента
ранговой
корреляции по формуле:
Коэффициент ранговой корреляции составит:

20.

Произвести
расчет
коэффициента
ранговой
корреляции по формуле:
Коэффициент ранговой корреляции составит:
6 × 38,5
231