Similar presentations:
Теория автоматов. Алгоритм работы автомата Мили
1.
2.
Автомат МилиОпределение: автоматом Мили называется пятерка объектов
Q, A, V, , λ = S, такая что
Q – множество внутренних состояний;
A – входной алфавит;
V – выходной алфавит;
: Q A Q – функция переходов;
λ : Q A V – функция выхода.
Таблица, задающая функции переходов и выхода, называется
таблицей состояний автомата.
2
3.
Диаграмма состояний автомата МилиОпределение: Диаграммой состояний автомата Мили называется
ориентированный граф вида:
количество
вершин
равно
количеству состояний
данного
автомата
Мили
и
помечено
символами внутренних состояний;
дуга, выходящая из любой вершины
qi, и заходящая в вершину qj,
помечена символами at, vr, которые
являются
результатом
работы
функций переходов δ(at, qi) = qj и
выхода λ(at, qi) = vr.
a1,v1
a2,v2
a2,v1
q0
q1
a2,v1
3
4.
Инициальность автоматаОпределение:
Автомат Мили называется инициальным, если он всегда
начинает работу из одного и того же состояния q1.
Автомат Мили называется неинициальным, если он может
начинать свою работу и любого своего состояния.
4
5.
Алгоритм работы автомата МилиОпределение: автомат Мили работает с двумя бесконечными
лентами, разбитыми на ячейки, так, что в одной ячейке может
быть записан один символ некоторого алфавита. Тактом времени
называется промежуток, за который автомат обрабатывает одну
ячейку.
Алгоритм: автомат считывает обозреваемый символ в ячейке
входной ленты, печатает в ячейку выходной ленты символ,
найденный с помощью функции выхода λ, двигается вдоль ленты
вправо и переходит в состояние, определяемое с помощью
функции перехода .
Критерий остановки: автомат останавливает работу, когда все
ячейки, содержащие символы данного слова, пройдены.
5
6.
ДешифраторОпределение:
дешифратором
называется
инициальный
конечный автомат, выходным алфавитом которого является
множество {0, 1}, для которого на вход подается бесконечная
последовательность символов некоторого алфавита и символ 1
печатается в том и только лишь том случае, если в данный момент
времени автомат обозревает последний символ уже считанного
слова α, фиксированного для данного автомата, а на ленте
записано слово, в которое входит α.
Слово α называется кодовой комбинацией автомата.
6
7.
Связность автоматаОпределение: неинициальный автомат называется сильно
связным, если для любых состояний автомата qi и qj найдется
слово α такое, что автомат, начавший работу в состоянии qi, при
считывании слова α переходит в состояние qj.
7
8.
Эквивалентность автоматовОпределение: состояния qi и qj неинициальных автоматов A1 и
A2 называются эквивалентными, если для любого слова α,
составленного из букв входного алфавита, выходные слова,
полученные при работе автоматов A1 и A2, запущенных,
соответственно из состояний qi и qj над словом α, равны.
Определение: автоматы A1 и A2 называются эквивалентными,
если для любого состояния qi автомата A1 найдется
эквивалентное ему состояние qj автомата A2, а также, если для
любого состояния q’j автомата A2 найдется эквивалентное ему
состояние q’i автомата A1.
8
9.
Минимальный автоматОпределение: автомат Аmin называется минимальным для
автомата А, если он является эквивалентным автомату А и
содержит наименьшее число внутренних состояний среди всех
автоматов, эквивалентных автомату А.
9
10.
Частичный автомат МилиОпределение:
автомат
Мили
называется
частичным
автоматом, если хотя бы одна из функций переходов или выхода
не является всюду определенной.
Определение: слово α называется применимым к состоянию qi
неинициального автомата, если функция переходов автомата,
начавшего работу в состоянии qi над словом α, может быть не
определена лишь после считывания последнего символа слова α.
Обозначение: неопределенный символ будем обозначать “–”.
10
11.
Покрытия словОпределение: слово α покрывает слово β, если слово β может
быть получено из α заменой некоторого множества (может быть,
пустого) символов неопределенными символами.
Определение: слово α совместимо со словом β, если существует
слово γ, покрывающее как слово α, так и слово β.
Обозначение: S(α,q) – выходное слово, полученное в результате
работы над словом α неинициального автомата S, запущенного
из состояния q.
Замечание: если на некотором наборе аргументов значение
выходной функции не определено, то в соответствующей
позиции выходного слова ставится неопределенный символ.
11
12.
Покрытия состоянийОпределение: состояние q’ автомата S’ покрывает состояние
автомата S, если любое слово α, применимое к состоянию q,
будет также применимо к состоянию q’, причем S’(α,q’) будет
покрывать S(α,q).
12
13.
Покрытия автоматовОпределение: частичный автомат S’ покрывает автомат S, если
для любого состояния q автомата S найдется покрывающее его
состояние q’ автомата S’.
Определение: автомат, покрывающий частичный автомат S и
имеющий наименьшее возможное число внутренних состояний
среди
всех
автоматов,
покрывающих
S,
называется
минимальным для S.
13
14.
Совместимые состоянияОпределение: состояния q и q’ частичного автомата S
называются совместимыми, если для любого слова α,
применимого к состояниям q и q’, слова S’(α,q’) и S(α,q) будут
совместимыми.
Определение: множество попарно совместимых состояний
автомата называется группой совместимости этого автомата.
14
15.
Группы совместимостиОпределение:
группа
совместимости
называется
максимальной, если при добавлении в нее любого состояния,
она перестает быть группой совместимости.
Определение: класс групп совместимости автомата S
называется группировкой, если любое состояние автомата S
попадает хотя бы в одну группу совместимости.
Определение: группировка, состоящая из всех максимальных
групп
совместимости
данного
автомата,
называется
максимальной группировкой данного автомата.
15
16.
Замкнутые группировкиОпределение: группировка называется замкнутой, если для
любой группы совместимости Qv этой группировки, для любого
символа входного алфавита a и для любых состояний q и q’ из
группы совместимости Qv, либо хотя бы одно из значений (α,q’)
и (α,q) не определено, либо (α,q’) и (α,q) определены и из
того, что (α,q) принадлежит некоторой группе совместимости
Qw, следует, что и (α,q’) также принадлежит Qw.
16
17.
Литература1. «Дискретная математика и математическая логика», Ю.А.
Аляев, С.Ф. Тюрин. – М.: Финансы и статистика, 2006.
2. «Дискретная математика и комбинаторика», Джеймс А.
Андерсон, пер. с англ. – М.: издательский дом «Вильямс», 2004.
3. «Дискретная математика», А.И. Белоусов, С.Б. Ткачев. – М.:
издательство МГТУ им. Н.Э. Баумана, 2004.
17
18.
19.
Задача 1Для кодового слова α = xyyxyyxx построить дешифратор с входным
алфавитом А = {x,y} и записать его в виде:
1. диаграммы состояний;
2. таблицы состояний.
19
20.
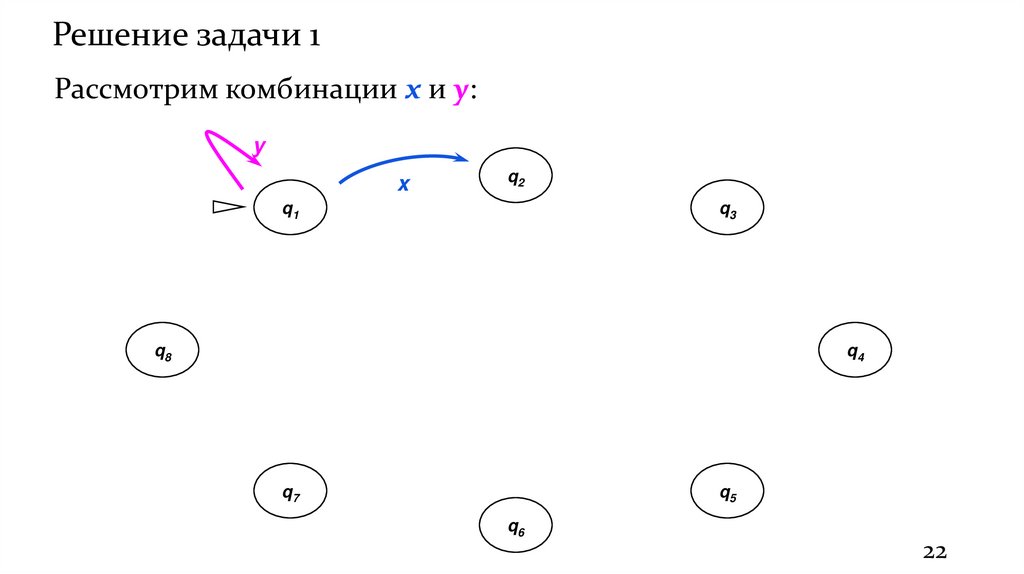
Решение задачи 11. Составим диаграмму состояний Q = {q1, q2, q3, q4, q5, q6, q7, q8}
q2
q1
q3
q8
q4
q7
q5
q6
20
21.
Решение задачи 12. Определим функцию выхода:
λ
x
y
q1
0
0
q2
0
0
q3
0
0
q4
0
0
q5
0
0
q6
0
0
q7
0
0
q8
1
0
3. Определим правило для задания функции переходов:
x1, x2, … , xk – начало кодового слова, то (xk,qk) = qk+1;
иначе (xk,qk) = qp+1, где p – наибольшее количество символов
xi,xi+1,…,xk, которые являются началом кодового слова.
21
22.
Решение задачи 1Рассмотрим комбинации x и y:
y
x
q2
q1
q3
q8
q4
q7
q5
q6
22
23.
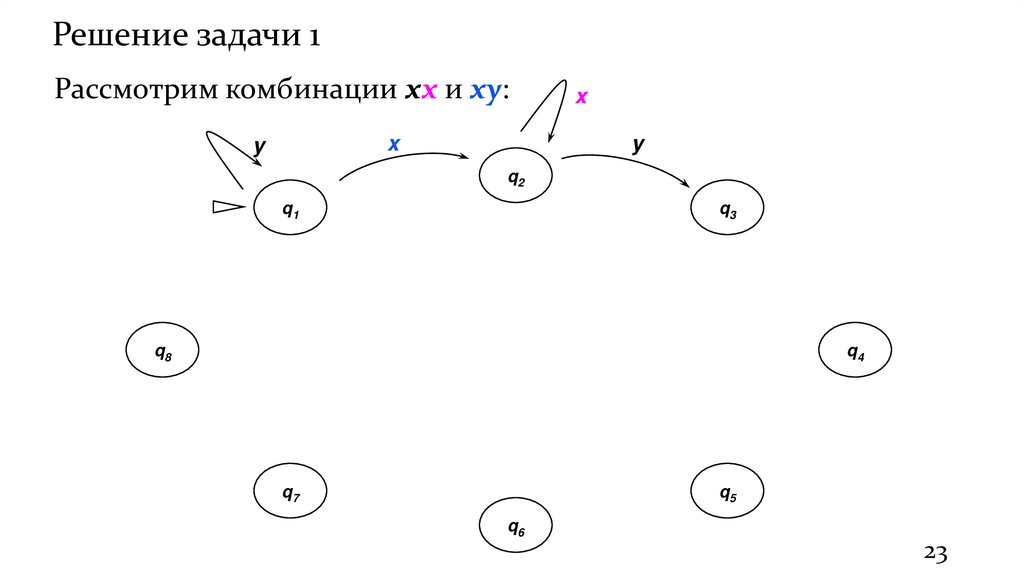
Решение задачи 1Рассмотрим комбинации xx и xy:
x
y
x
y
q2
q1
q3
q8
q4
q7
q5
q6
23
24.
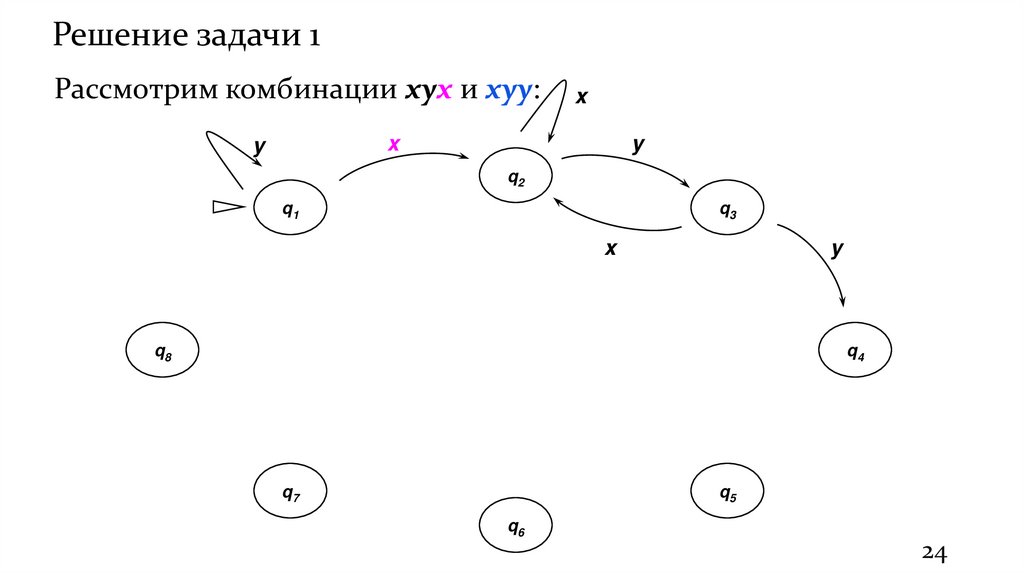
Решение задачи 1Рассмотрим комбинации xyx и xyy:
x
x
y
y
q2
q1
q3
x
y
q8
q4
q7
q5
q6
24
25.
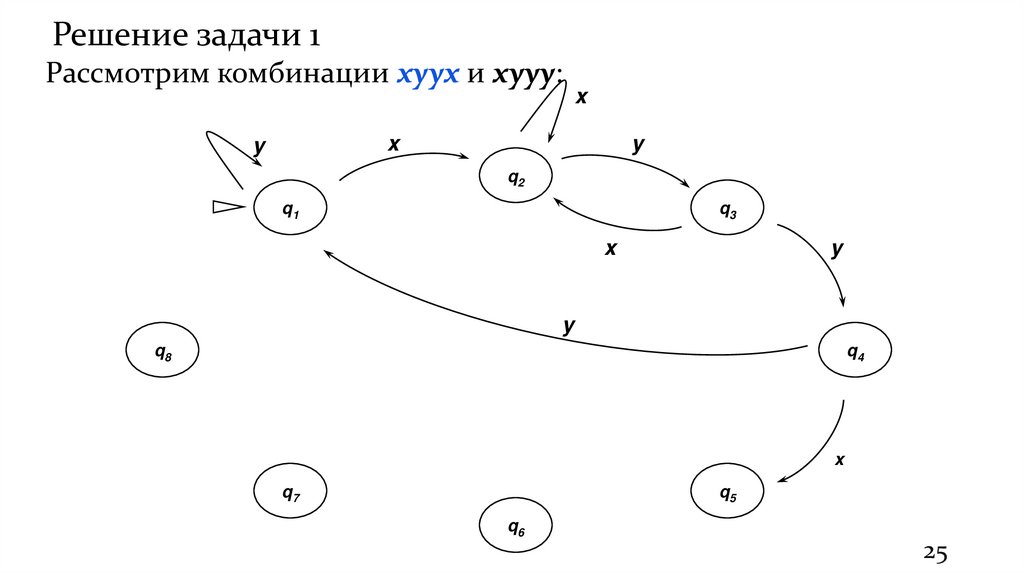
Решение задачи 1Рассмотрим комбинации xyyx и xyyy:
x
x
y
y
q2
q1
q3
x
y
y
q8
q4
x
q7
q5
q6
25
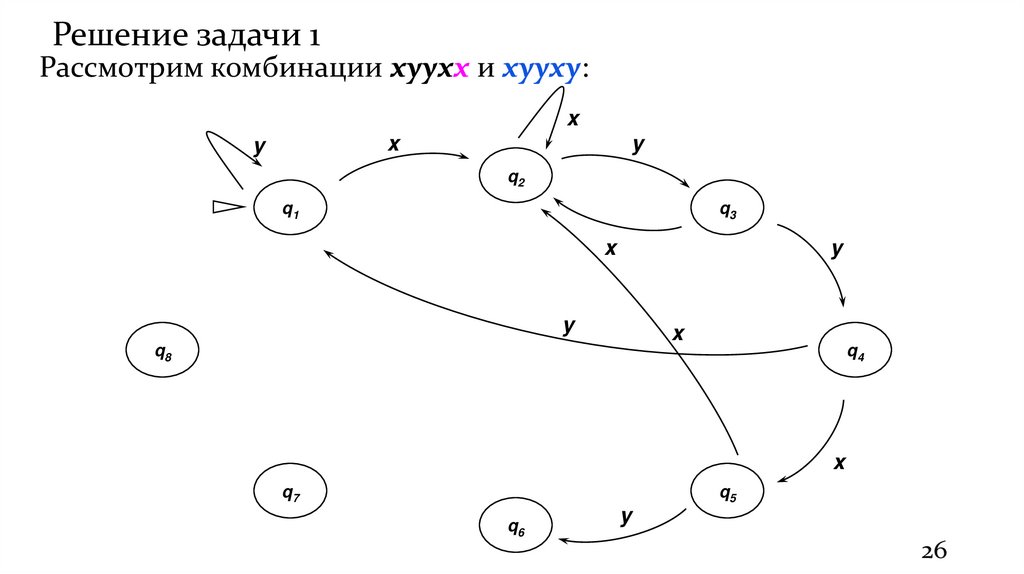
26.
Решение задачи 1Рассмотрим комбинации xyyxx и xyyxy:
x
x
y
y
q2
q1
q3
x
y
y
x
q8
q4
x
q7
q5
q6
y
26
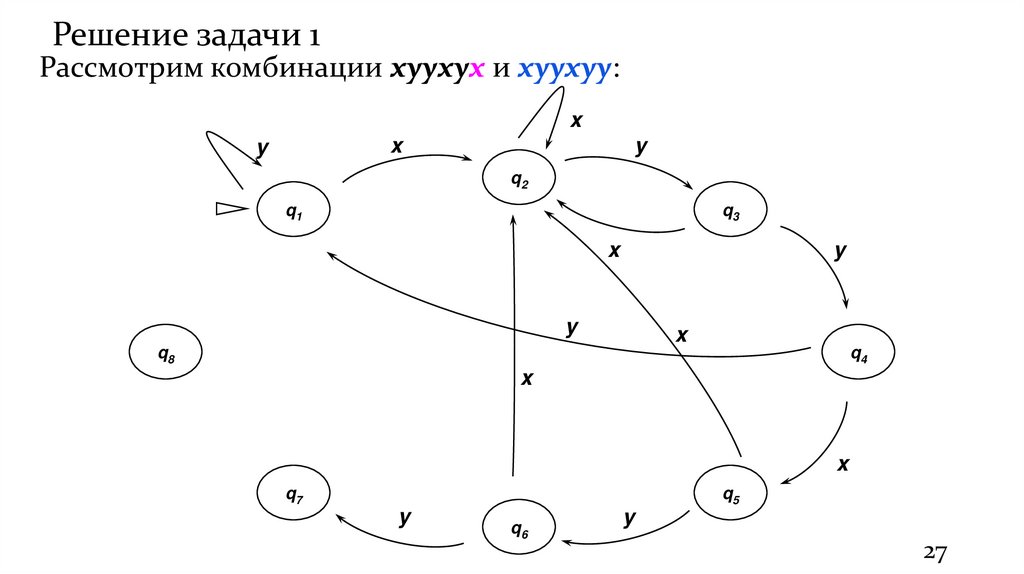
27.
Решение задачи 1Рассмотрим комбинации xyyxyx и xyyxyy:
x
x
y
y
q2
q1
q3
x
y
y
x
q8
q4
x
x
q7
q5
y
q6
y
27
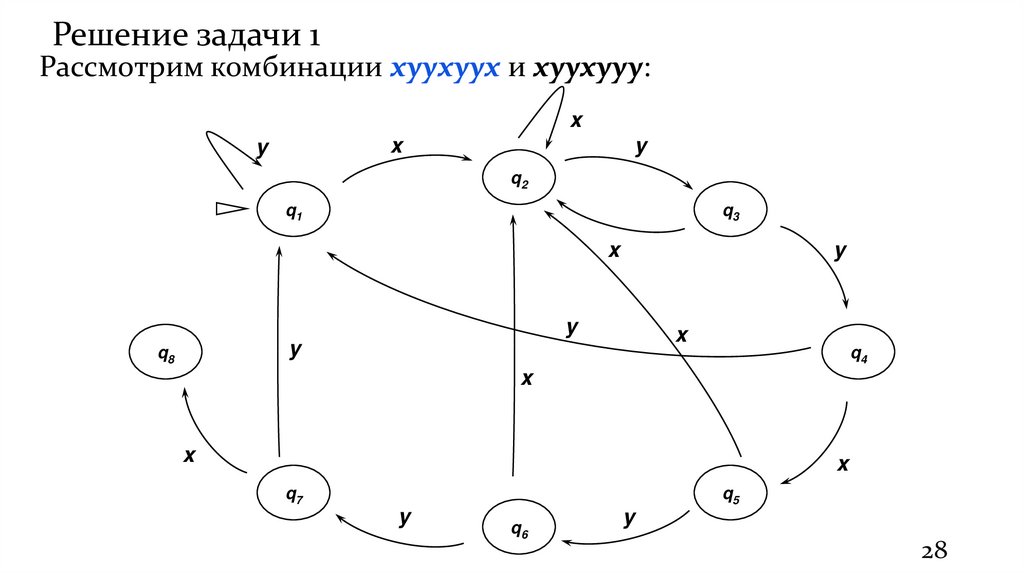
28.
Решение задачи 1Рассмотрим комбинации xyyxyyx и xyyxyyy:
x
x
y
y
q2
q1
q3
x
y
y
x
y
q8
q4
x
x
x
q7
q5
y
q6
y
28
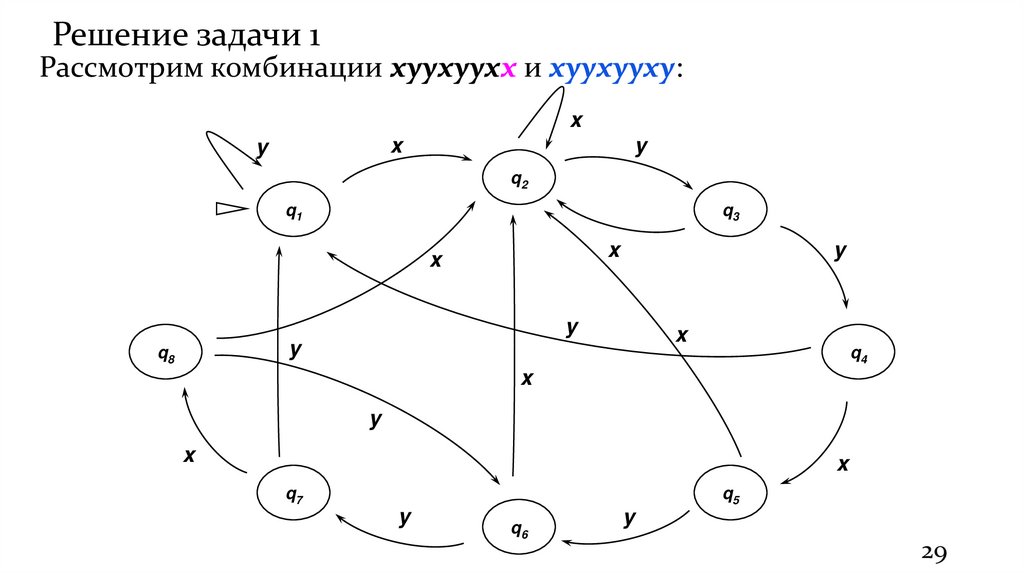
29.
Решение задачи 1Рассмотрим комбинации xyyxyyxx и xyyxyyxy:
x
x
y
y
q2
q1
q3
x
x
y
y
x
y
q8
q4
x
y
x
x
q7
q5
y
q6
y
29
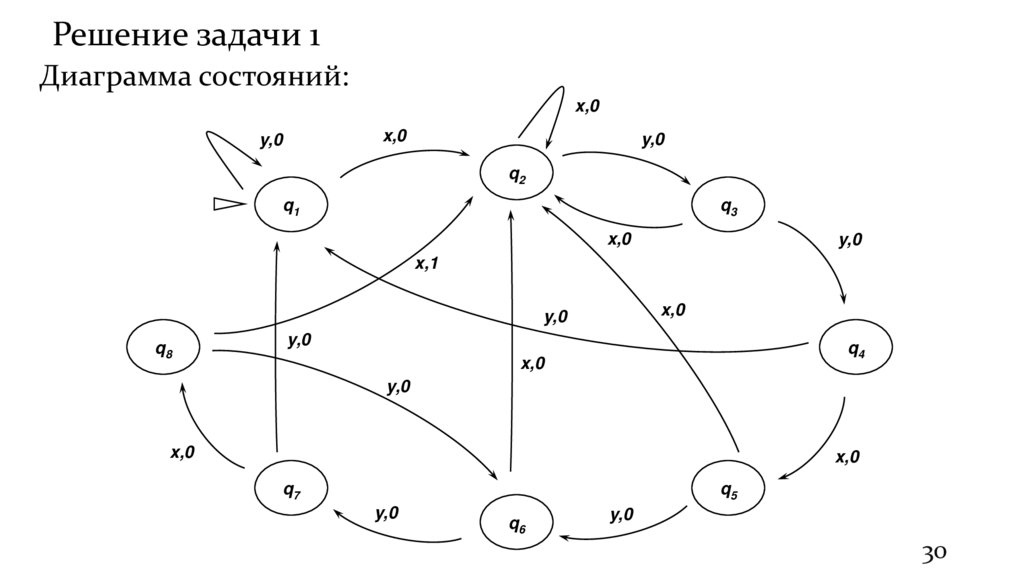
30.
Решение задачи 1Диаграмма состояний:
x,0
x,0
y,0
y,0
q2
q1
q3
x,0
y,0
x,1
x,0
y,0
q8
y,0
q4
x,0
y,0
x,0
x,0
q7
q5
y,0
q6
y,0
30
31.
Решение задачи 1Составим таблицу состояний:
λ
q1
q2
q3
q4
q5
q6
q7
q8
x
0
0
0
0
0
0
0
1
y
0
0
0
0
0
0
0
0
δ
q1
q2
q3
q4
q5
q6
q7
q8
x
q2
q2
q2
q5
q2
q2
q8
q2
y
q1
q3
q4
q1
q6
q7
q1
q6
Q
q1
q2
q3
q4
q5
q6
q7
q8
x
q2,0
q2,0
q2,0
q5,0
q2,0
q2,0
q8,0
q2,1
y
q1,0
q3,0
q4,0
q1,0
q6,0
q7,0
q1,0
q6,0
A
31
32.
Задача 2Для кодового слова α = xxyxxyyx построить дешифратор с входным
алфавитом А = {x,y} и записать его в виде:
1. диаграммы состояний;
2. таблицы состояний.
32
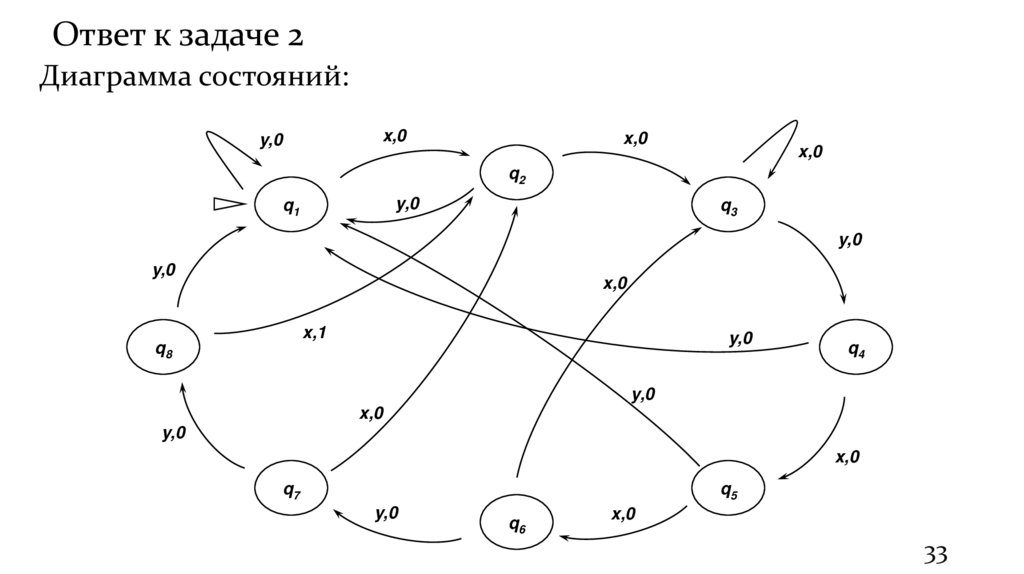
33.
Ответ к задаче 2Диаграмма состояний:
x,0
y,0
x,0
x,0
q2
y,0
q1
q3
y,0
y,0
x,0
x,1
q8
y,0
q4
y,0
x,0
y,0
x,0
q7
q5
y,0
q6
x,0
33
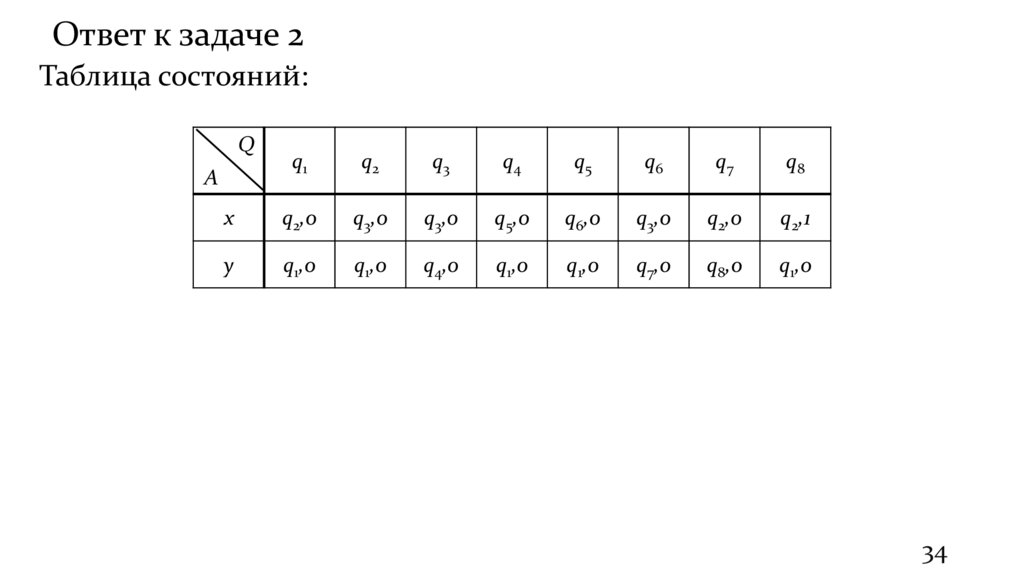
34.
Ответ к задаче 2Таблица состояний:
Q
q1
q2
q3
q4
q5
q6
q7
q8
x
q2,0
q3,0
q3,0
q5,0
q6,0
q3,0
q2,0
q2,1
y
q1,0
q1,0
q4,0
q1,0
q1,0
q7,0
q8,0
q1,0
A
34
35.
Задача 3Для кодового слова α = babaaaba построить дешифратор с входным
алфавитом А = {a,b} и записать его в виде:
1. диаграммы состояний;
2. таблицы состояний.
35
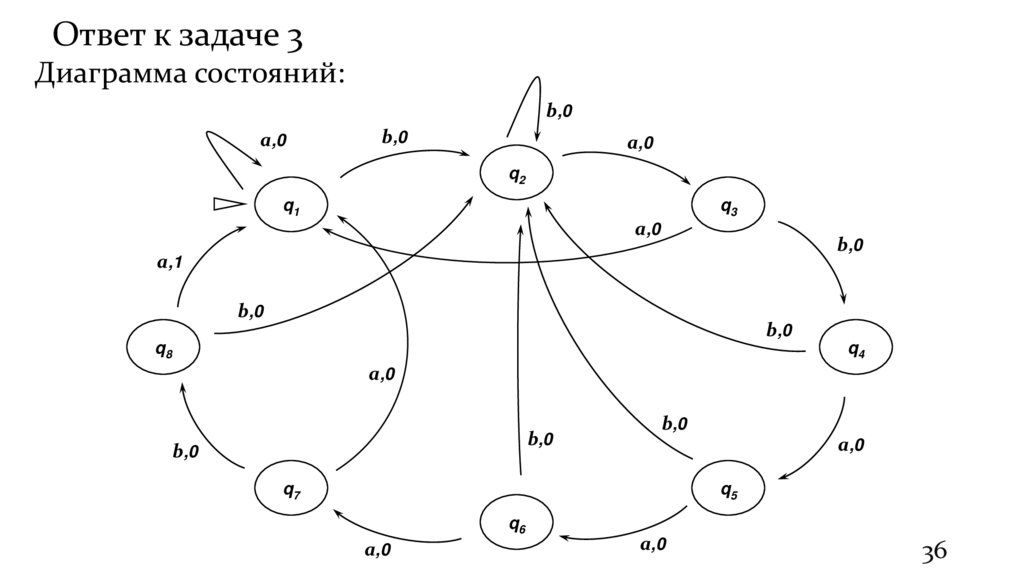
36.
Ответ к задаче 3Диаграмма состояний:
b,0
a,0
b,0
a,0
q2
q1
q3
a,0
b,0
a,1
b,0
b,0
q8
q4
a,0
b,0
b,0
b,0
a,0
q7
q5
q6
a,0
a,0
36
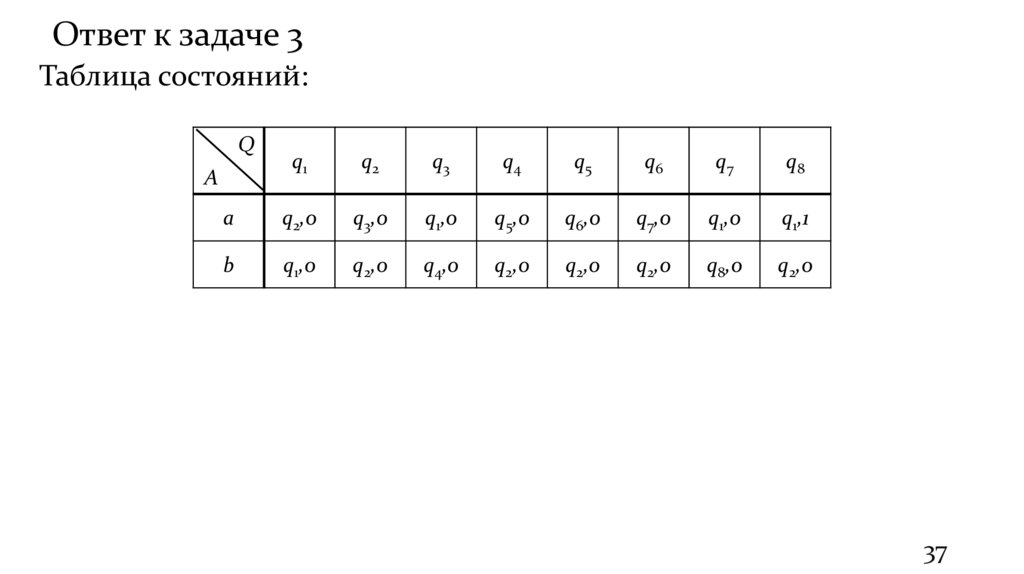
37.
Ответ к задаче 3Таблица состояний:
Q
q1
q2
q3
q4
q5
q6
q7
q8
a
q2,0
q3,0
q1,0
q5,0
q6,0
q7,0
q1,0
q1,1
b
q1,0
q2,0
q4,0
q2,0
q2,0
q2,0
q8,0
q2,0
A
37
38.
Задача 4Для кодового слова α = 00001010 построить дешифратор с входным
алфавитом А = {0,1} и записать его в виде:
1. диаграммы состояний;
2. таблицы состояний.
38
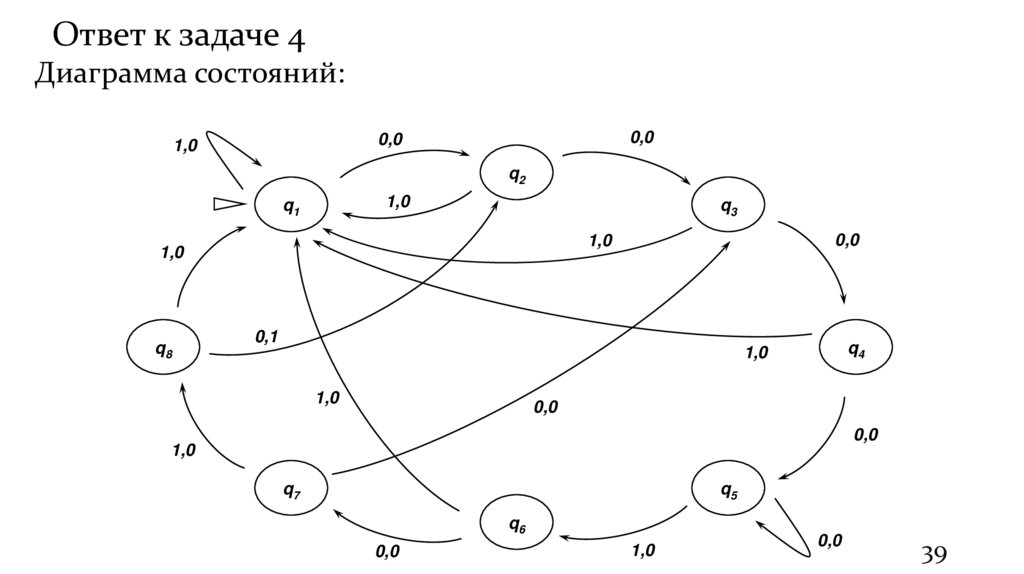
39.
Ответ к задаче 4Диаграмма состояний:
0,0
0,0
1,0
q2
1,0
q1
q3
q8
0,0
1,0
1,0
0,1
q4
1,0
1,0
0,0
0,0
1,0
q7
q5
q6
0,0
1,0
0,0
39
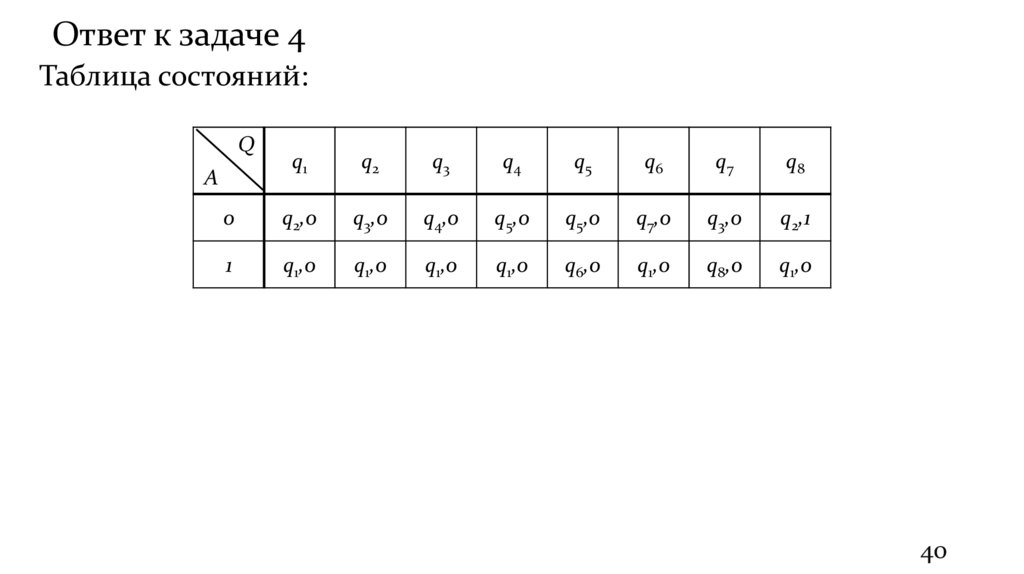
40.
Ответ к задаче 4Таблица состояний:
Q
q1
q2
q3
q4
q5
q6
q7
q8
0
q2,0
q3,0
q4,0
q5,0
q5,0
q7,0
q3,0
q2,1
1
q1,0
q1,0
q1,0
q1,0
q6,0
q1,0
q8,0
q1,0
A
40
41.
Задача 5Дана таблица состояний конечного автомата со множеством
состояний Q = {1,2,3,4,5,6,7,8,9}, входным алфавитом A = {a,b} и
выходным алфавитом V = {x, y}.
Q
1
2
3
4
5
6
7
8
9
a
5,x
3,y
7,x
5,x
6,y
9,x
6,y
4,y
1,y
b
2,y
1,x
9,y
8,y
7,x
5,y
5,x
3,x
4,x
A
1. Выяснить, является ли автомат сильно связным;
2. построить эквивалентный минимальный автомат;
3. проверить работу исходного и минимального автоматов над
словом “abbabaab”.
41
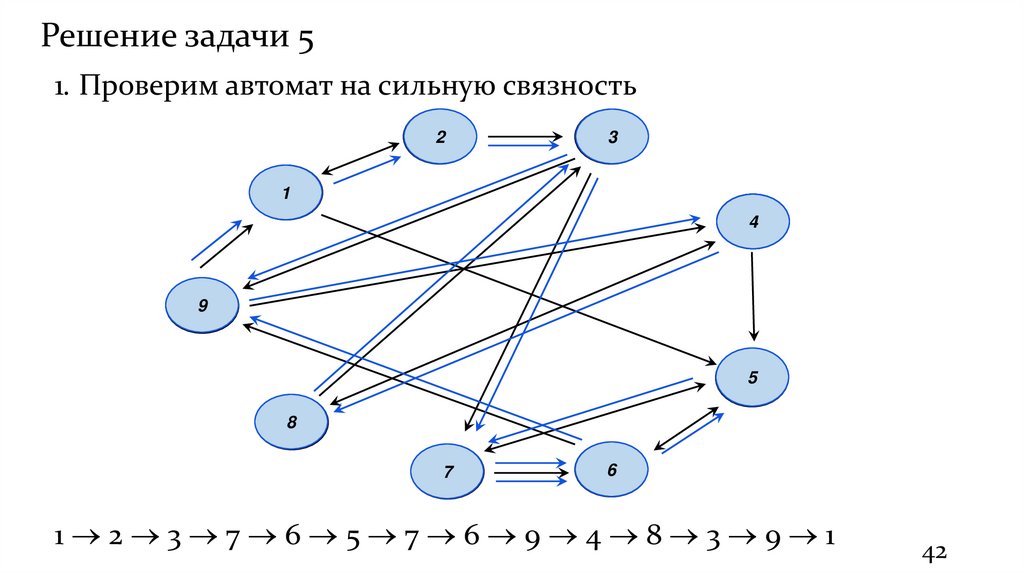
42.
Решение задачи 51. Проверим автомат на сильную связность
2
3
1
4
9
5
8
7
6
1 2 3 7 6 5 7 6 9 4 8 3 9 1
42
43.
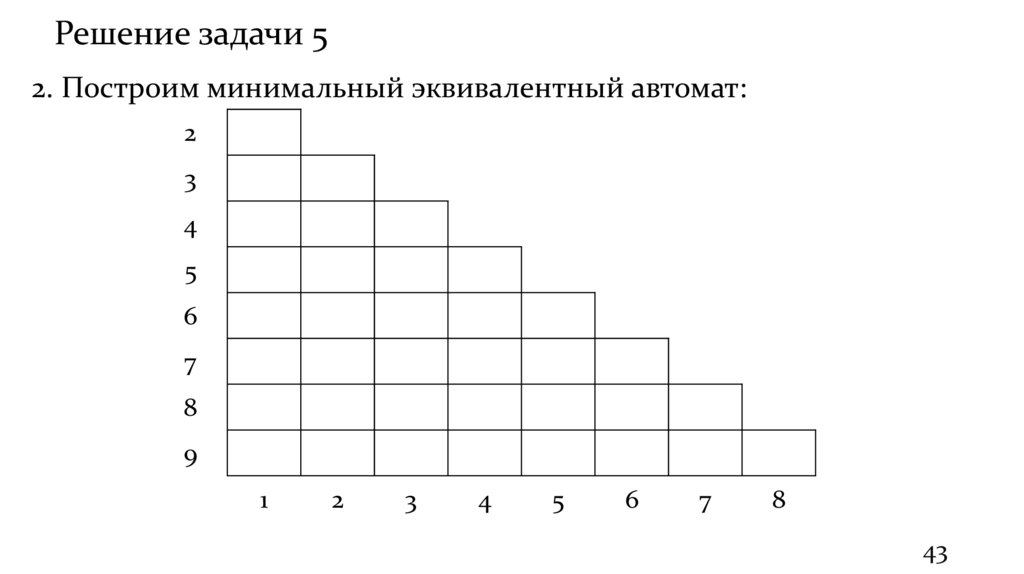
Решение задачи 52. Построим минимальный эквивалентный автомат:
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
43
44.
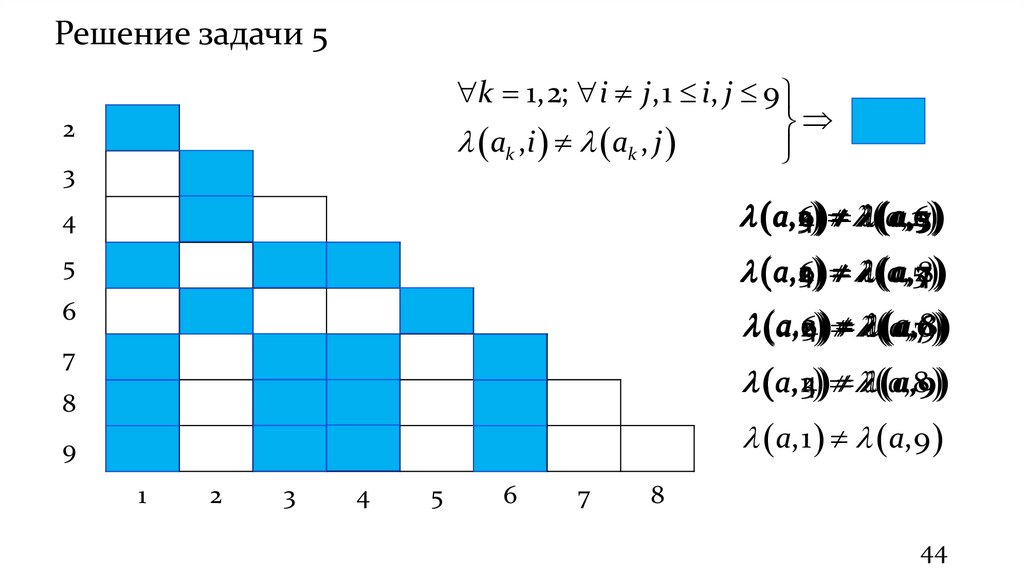
Решение задачи 5k 1,2; i j ,1 i, j 9
ak ,i ak , j
2
3
4
,3
,5
,1
,2 aa,2
,3
a,5
,6
,6
,7
,4
5
a,4
,3
,7
,1 aa,5
,2
,4
,6
,8
6
a,2
,3
,8
,4 aa,7
,6
,1
,6
,9
7
a,1
,4
,9
,3 aa,8
8
a,1 a,9
9
1
2
3
4
5
6
7
8
44
45.
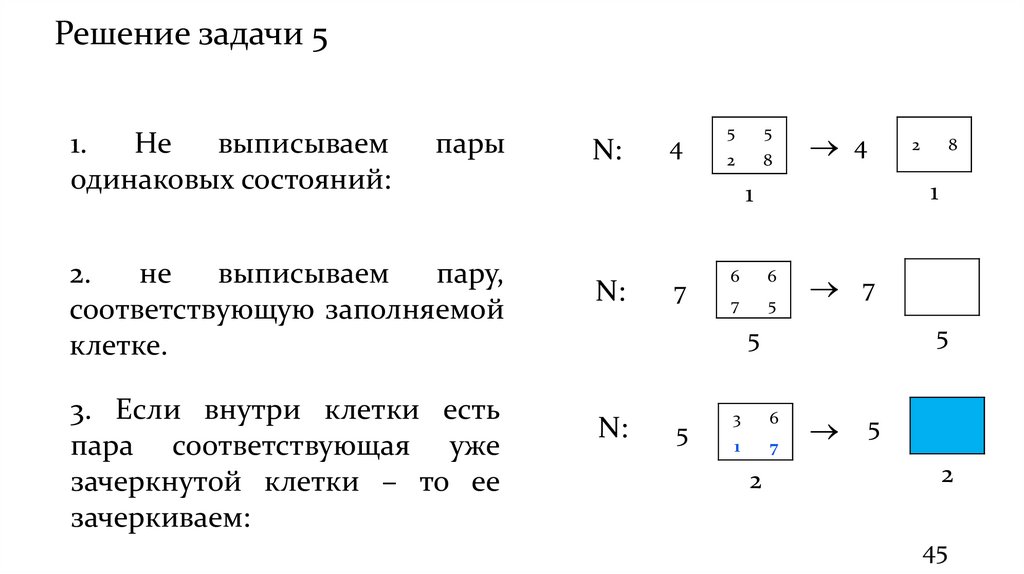
Решение задачи 51.
Не
выписываем
одинаковых состояний:
пары
2.
не
выписываем
пару,
соответствующую заполняемой
клетке.
3. Если внутри клетки есть
пара соответствующая уже
зачеркнутой клетки – то ее
зачеркиваем:
N:
4
5
5
2
8
4
7
6
6
7
5
7
5
5
N:
5
3
6
1
7
2
8
1
1
N:
2
5
2
45
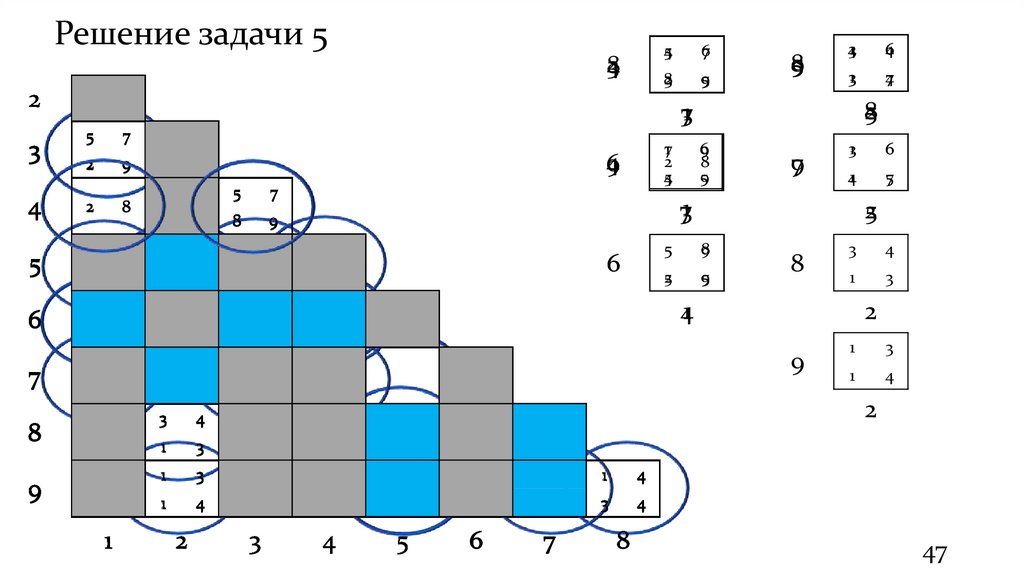
46.
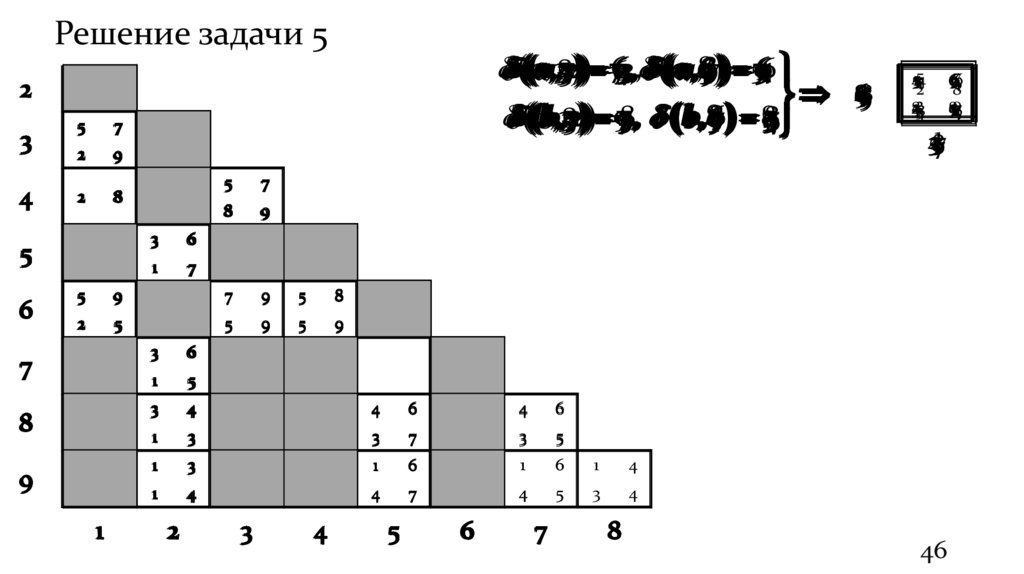
Решение задачи 5,5
6,
,8
,7
6
6,
,8
aaaa,3
,4
,2
,1
,2 7,
5,
3,
3, aaaa,4
,4
,3
,6
,5
,7 59
754
9
,7
,9
146
,6
,8
4,
6984759438
,5
7,
,7
5835
,8
bbbb,3
,4
8,
,2
,1
,2 9,
2,
1,1, bbb,4
,8
,4
,5
,3
,6 8
734
9
,7
5,
,9
,8
3,
2
3
4
5
7
2
9
2
8
5
6
3
6
1
7
5
7
8
9
5
9
7
9
5
8
2
5
5
9
5
9
7
8
9
1
3
6
1
5
3
4
4
6
4
6
1
3
3
7
3
5
1
3
1
6
1
6
1
4
1
4
4
7
4
5
3
4
2
3
4
5
6
7
8
4
5317154
21
8
53251243
4
9
6
749
6
34766
8
9
9
8
7359
7455
1571
4
5328
46
47.
Решение задачи 583
4
2
3
4
7
6
23
8
9
5
9
8
5
431
6
4
31
4
7
8
25
731
5
7
2
9
2
3
6
1
7
5
7
8
9
6
9
7
9
5
8
2
5
5
9
5
9
8
9
1
9
7
6
41
75
25
5
9
8
52
9
5
8
1
5
3
4
4
6
4
6
1
3
3
7
3
5
1
3
1
6
1
6
1
4
1
4
4
7
4
5
3
4
4
3
4
1
3
2
9
6
3
31
41
3
2
6
9
8
59
731
5
7
71
2
4
5
4
9
6
8
5
6
5
4
5
6
7
1
3
1
4
2
8
47
48.
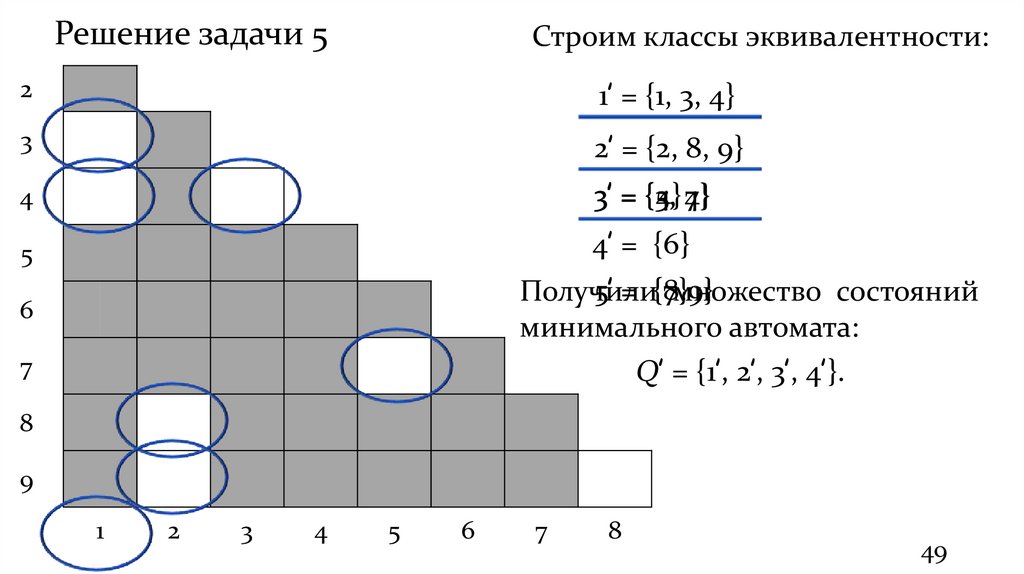
Решение задачи 5Строим классы эквивалентности:
2
1’ = {1, 3, 4}
3
2’ = {2, 8, 9}
4
{4} 4}
3’ = {5,
{3,
7}
5
4’ = {6}
5’ = {8,9}
{7}
Получили
множество состояний
минимального автомата:
Q’ = {1’, 2’, 3’, 4’}.
6
7
8
9
1
2
3
4
5
6
7
8
49
49.
Решение задачи 5Найдем значения функции переходов:
q1 , q2 i ; i 1,4 a j , q1 a j , q2 , j 1,2
q1 i1 , q2 i2 : a j , q1 q2 a j ,i i2
Например:
Аналогично:
a,1 5 5 3 a,1 3
1 1
b,1 2 2 2 b,1 2
a,2 1 , b,2 1
a,3 4 , b,3 3
a,4 2 , b,4 3
50
50.
Решение задачи 5Найдем значения функции выхода:
q1 , q2 i ; i 1,4 a j , q1 a j , q2 , j 1,2
q1 i : a j , q1 ak a j ,i ak
Например: 1 1
Аналогично:
a,1 x a,1 x
b,1 y b,1 y
a,2 y, b,2 x
a,3 y, b,3 x
a,4 x , b,4 y
51
51.
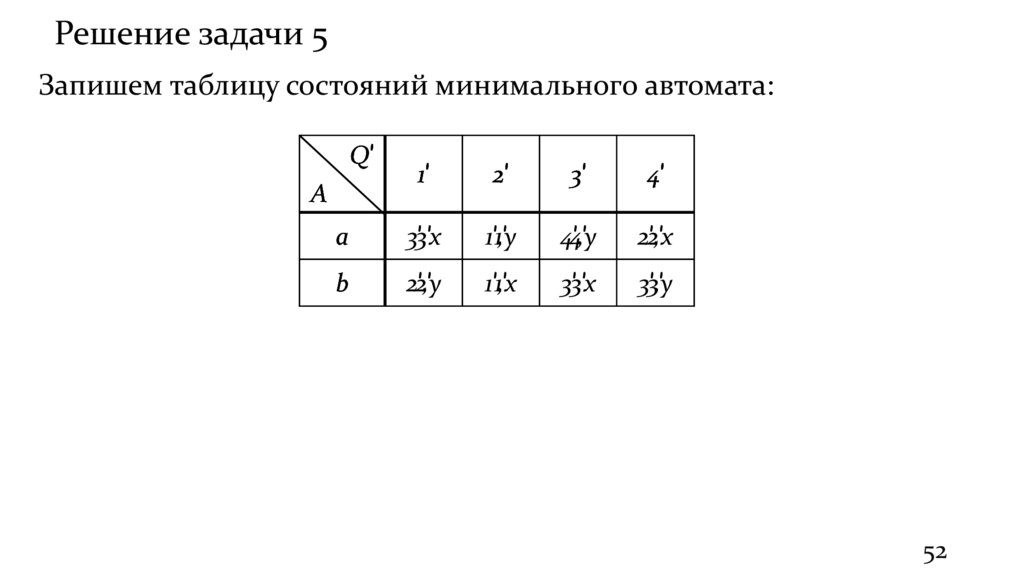
Решение задачи 5Запишем таблицу состояний минимального автомата:
Q’
1’
2’
3’
4’
a
3’,x
3’
1’,y
1’
4’,y
4’
2’,x
2’
b
2’,y
2’
1’,x
1’
3’,x
3’
3’,y
3’
A
52
52.
Решение задачи 53. Проверим работу исходного автомата над словом “abbabaab”:
Входное слово
a
b
b
a
b
a
a
b
Состояния
1
5
7
5
6
5
6
9
4
Выходное слово
x
x
x
y
y
y
x
x
Проверим работу минимального автомата над словом “abbabaab”:
Входное слово
a
b
b
a
b
a
a
b
Состояния
1’
3’
3’
3’
4’
3’
4’
2’
1’
Выходное слово
x
x
x
y
y
y
x
x
53
53.
Задача 6Дана таблица состояний конечного автомата со множеством
состояний Q = {1,2,3,4,5,6,7,8,9}, входным алфавитом A = {a,b} и
выходным алфавитом V = {x, y}.
Q
1
2
3
4
5
6
7
8
9
a
4,x
3,y
7,x
5,x
8,x
7,x
2,y
5,x
2,y
b
7,y
4,y
9,x
9,y
7,y
9,y
8,x
9,y
5,x
A
1. Выяснить, является ли автомат сильно связным;
2. построить эквивалентный минимальный автомат;
3. проверить работу исходного и минимального автоматов над
словом “ababab”.
54
54.
Ответ к задаче 61. Автомат не сильно связный (состояния 1 и 6 недостижимы).
2. Таблица состояний минимального автомата S’:
Q’
1’
2’
3’
4’
5’
a
1’,x
3’,y
5’,x
5’,x
2’,y
b
5’,y
1’,y
5’,x
5’,y
1’,x
A
3. S(ababab, 1) = S’(ababab, 1’) = xyyyxy
55
55.
Задача 7Дана таблица состояний конечного автомата со множеством
состояний Q = {1,2,3,4,5,6,7,8,9}, входным алфавитом A = {a,b} и
выходным алфавитом V = {x, y}.
Q
1
2
3
4
5
6
7
8
9
a
2,x
1,x
5,x
7,x
3,x
5,x
8,x
9,x
4,x
b
3,x
5,y
1,y
9,x
2,x
1,y
4,y
7,x
8,y
A
1. Выяснить, является ли автомат сильно связным;
2. построить эквивалентный минимальный автомат;
3. проверить работу исходного и минимального автоматов над
словом “aaabbb”.
56
56.
Ответ к задаче 71. Автомат не сильно связный (состояние 6 недостижимо).
2. Таблица состояний минимального автомата S’:
Q’
1’
2’
a
2’,x
1’,x
b
2’,x
1’,y
A
3. S(aaabbb, 1) = S’(aaabbb, 1’) = xxxyxy
57
57.
58.
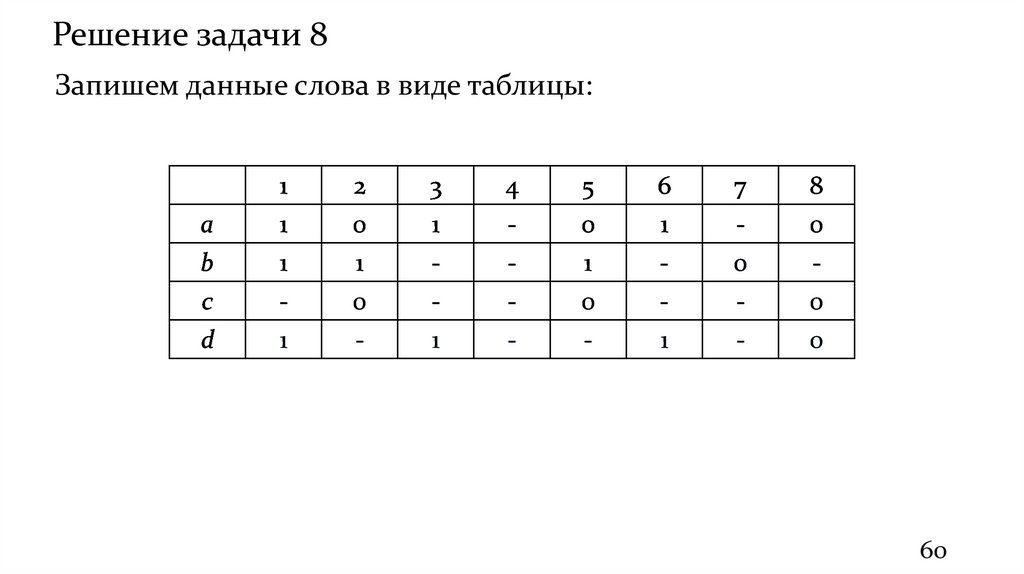
Задача 8Даны слова a = 101-01-0, b = 11--1-0-, c = -0--0--0 и d = 1-1--1-0.
1. Найти все пары слов (x,y) такие, что слово x покрывает слово y;
2. найти все пары совместимых слов;
3. найти все пары несовместимых слов;
4. найти слово x, не принадлежащее множеству {a,b,c,d}, такое что
слово x покрывает три слова из множества {a,b,c,d}.
59
59.
Решение задачи 8Запишем данные слова в виде таблицы:
a
1
1
2
0
3
1
4
-
5
0
6
1
7
-
8
0
b
c
d
1
1
1
0
-
1
-
1
0
-
1
0
-
0
0
60
60.
Решение задачи 81. Найдем пары (x,y), такие что x покрывает y:
a
b
1
1
1
2
0
1
3
1
-
4
-
5
0
1
6
1
-
7
0
8
0
-
c
d
1
0
-
1
-
0
-
1
-
0
0
(a,c) (a,d)
(a,c);
61
61.
Решение задачи 82 и 3. Найдем пары совместимых и несовместимых слов:
Если слово x покрывает слово y, то они совместимы (γ = x)
(a,c); (a,d)
Если слово x покрывает слово y и слово z, то слова y и z
совместимы (γ = x)
(c,d)
62
62.
Решение задачи 81
2
3
4
5
6
7
8
a
b
c
1
1
-
0
1
0
1
-
-
0
1
0
1
-
0
-
0
0
d
1
-
1
-
-
1
-
0
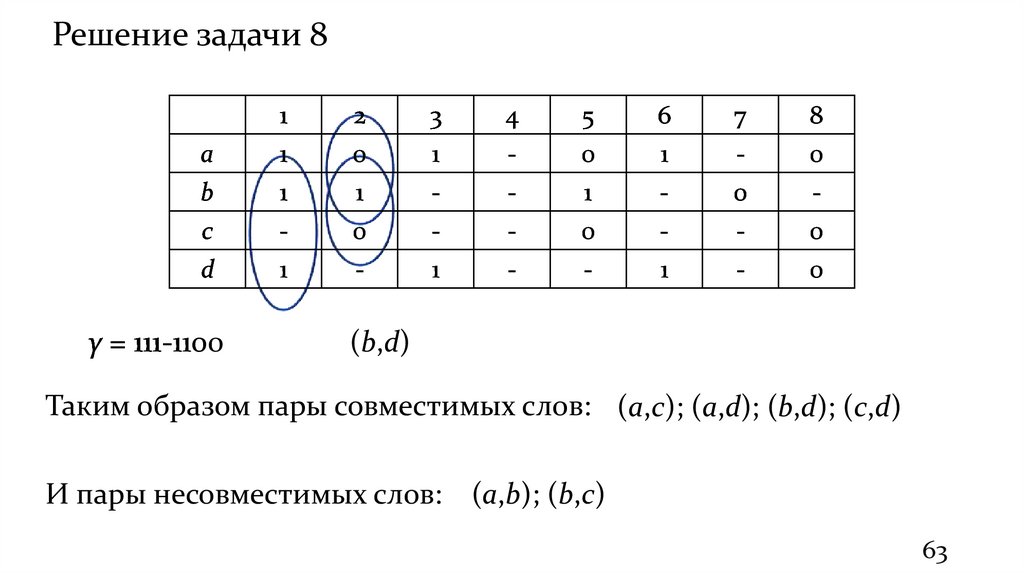
γ = 111-110
1
111-1100
11
111
111111-1
111-11
(b,d)
Таким образом пары совместимых слов: (a,с); (a,d); (b,d); (c,d)
И пары несовместимых слов: (a,b); (b,c)
63
63.
Решение задачи 84. Найдем слово x, не принадлежащее множеству {a,b,c,d}, такое что
слово x покрывает не менее двух слов из множества {a,b,c,d} :
Слово a покрывает слова c и d:
a
x4231
1
1
1
2
0
0
3
1
1
a = 101-01-0
4
0-1
5
0
0
x1 = 101101-0 x2 = 101001-0 x3 = 101-0110
6
1
1
7
0-1
8
0
0
x4 = 101-0100
x5 = 10110110 x6 = 10100100 x7 = 10110100 x8 = 10100110
64
64.
Задача 9Даны слова a = 1--00--0---0, b = 11-00-101-10, c = -1-0--1--11- и
d = 111-0-000-10.
1. Найти все пары слов (x,y) такие, что слово x покрывает слово y;
2. найти все пары совместимых слов;
3. найти все пары несовместимых слов;
4. найти слово x, не принадлежащее множеству {a,b,c,d}, такое что
слово x покрывает три слова из множества {a,b,c,d}.
65
65.
Ответ к задаче 91. (b,a); (d,a).
2. (a,b); (a,c); (a,d); (b,c).
3. (b,d); (c,d).
4. x = 11-00-101110 покрывает a, b, и c.
66
66.
Задача 10Даны слова a = -10--0-1---0, b = 1-0--11-10-0, c = -101-0--11-0 и
d = --01-0--11-0.
1. Найти все пары слов (x,y) такие, что слово x покрывает слово y;
2. найти все пары совместимых слов;
3. найти все пары несовместимых слов;
4. найти слово x, не принадлежащее множеству {a,b,c,d}, такое что
слово x покрывает три слова из множества {a,b,c,d}.
67
67.
Ответ к задаче 101. (c,d).
2. (a,c); (a,d); (c,d).
3. (a,b); (b,c); (b,d).
4. x = -101-0-111-0 покрывает a, c, и d.
68
68.
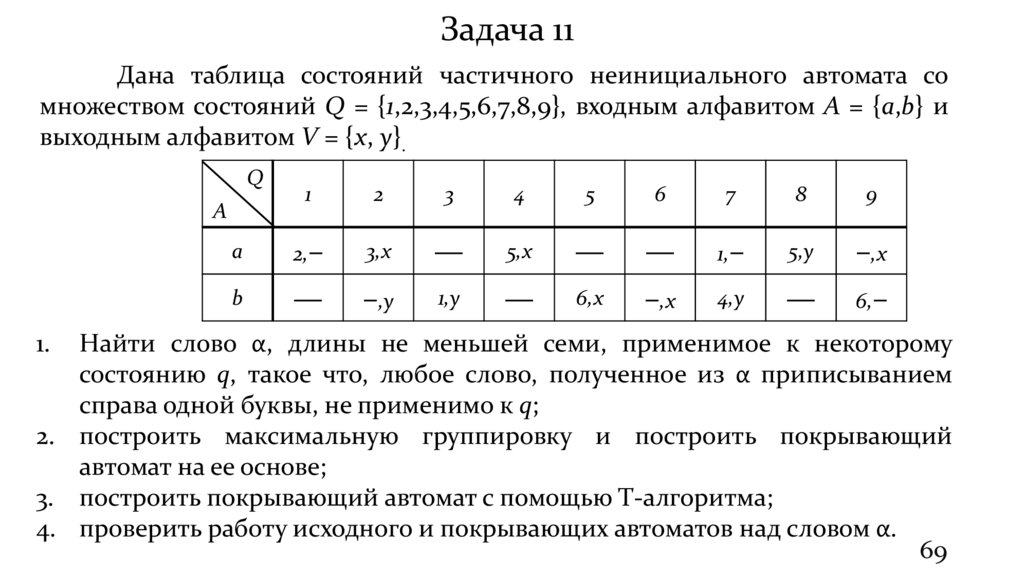
Задача 11Дана таблица состояний частичного неинициального автомата со
множеством состояний Q = {1,2,3,4,5,6,7,8,9}, входным алфавитом A = {a,b} и
выходным алфавитом V = {x, y}.
Q
1
2
3
4
5
6
7
8
9
a
2,–
3,x
—
5,x
—
—
1,–
5,y
–,x
b
—
–,y
1,y
—
6,x
–,x
4,y
—
6,–
A
1.
Найти слово α, длины не меньшей семи, применимое к некоторому
состоянию q, такое что, любое слово, полученное из α приписыванием
справа одной буквы, не применимо к q;
2. построить максимальную группировку и построить покрывающий
автомат на ее основе;
3. построить покрывающий автомат с помощью Т-алгоритма;
4. проверить работу исходного и покрывающих автоматов над словом α.
69
69.
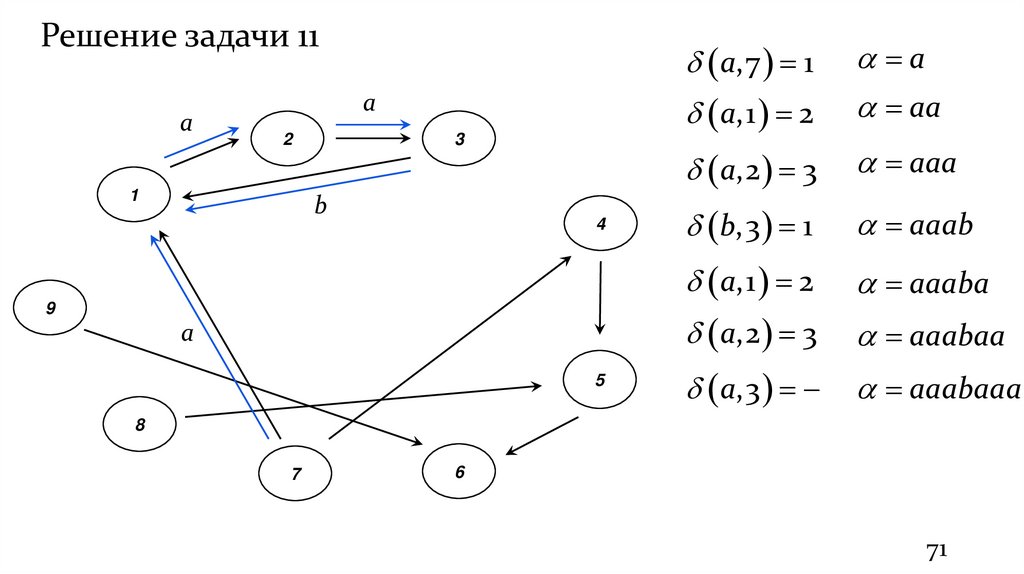
Решение задачи 111. Найдем слово α, длины не меньшей семи, применимое к
некоторому состоянию q, такое что, любое слово, полученное из α
приписыванием справа одной буквы, не применимо к q.
Слово α применимо к состоянию q, если можно прочитать все
символы данного слова.
Слово α неприменимо к состоянию q, если при прочтении
некоторого символа, функция переходов не определена.
70
70.
Решение задачи 11a
a,7 1
a
3
2
1
b
4
9
a
5
a,1 2
a
aa
a,2 3
aaa
b,3 1
aaab
a,1 2
aaaba
a,2 3
aaabaa
a,3
aaabaaa
8
7
6
71
71.
Решение задачи 10Проверим работу исходного автомата над словом “aaabaaa”:
Входное слово
a
a
a
b
a
a
a
Состояния
7
1
2
3
1
2
3
–
Выходное слово
–
–
x
y
–
x
–
Получили слово β = --xy-x-
72
72.
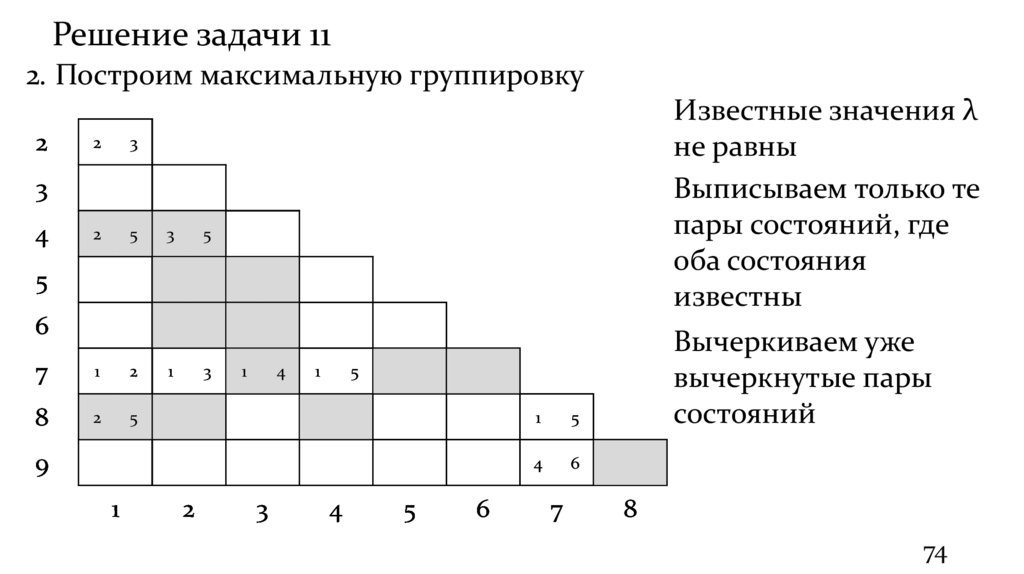
Решение задачи 112. Построим максимальную группировку
2
2
3
2
5
Известные значения λ
не равны
Выписываем только те
пары состояний, где
оба состояния
известны
3
4
3
5
5
6
7
1
2
8
2
5
1
3
1
4
1
5
9
1
2
3
Вычеркиваем уже
вычеркнутые пары
состояний
4
5
6
1
5
4
6
7
8
74
73.
Решение задачи 11Алгоритм построения максимальной группировки:
Шаг 0: Q00 состоит из всех возможных состояний
Шаг i: рассматривается i-ое состояние
если i Qi 1,k Qi ,k Qi 1,k
Qi ,k Qi 1,k \ qi
если qi Qi 1,k
Qi ,k 1 Qi 1,k \ q j , q j не совместные с qi , j 1..n
если Qi ,k Q j ,l Qi ,k на следующем шаге не рассматривается
75
74.
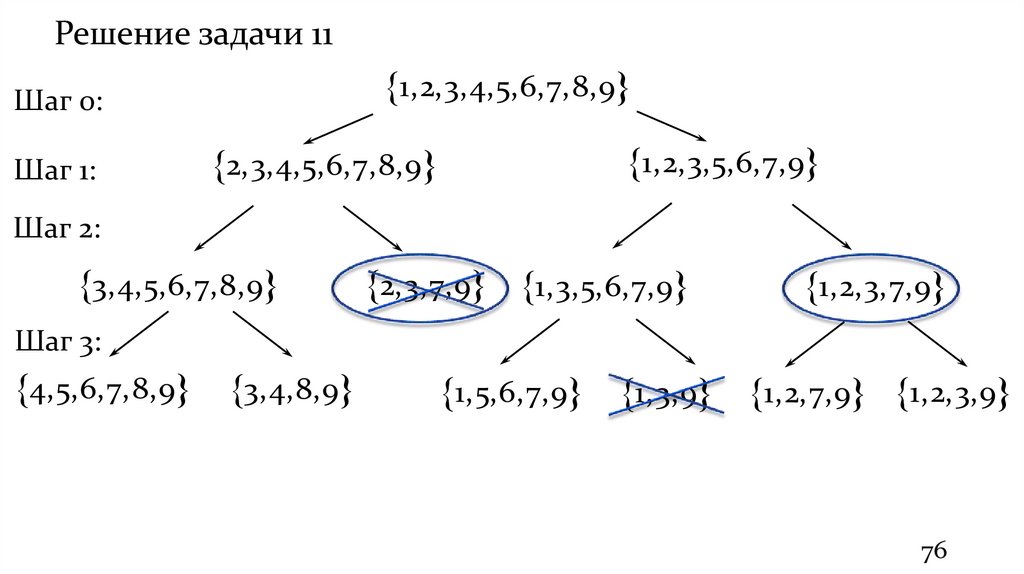
Решение задачи 111,2,3,4,5,6,7,8,9
Шаг 0:
Шаг 1:
2,3,4,5,6,7,8,9
1,2,3,5,6,7,9
Шаг 2:
3,4,5,6,7,8,9
2,3,7,9 1,3,5,6,7,9
1,2,3,7,9
Шаг 3:
4,5,6,7,8,9
3,4,8,9
1,5,6,7,9 1,3,9 1,2,7,9 1,2,3,9
76
75.
Решение задачи 11Шаг 4: 5,6,7,8,9 4,5,6,7,9 3,8,9 3,4,9 1,5,6,7,9 1,2,7,9 1,2,3,9
6,7,8,9 5,6,8,9 4,6,7,9 4,5,6,9 3,8,9 3,4,9
1,6,7,9 1,5,6,9 1,2,7,9 1,2,3,9
Шаг 6: 7,8,9 6,8,9 5,8,9 5,6,8,9 4,7,9 4,6,9 4,5,9 4,5,6,9
3,8,9 3,4,9 1,7,9 1,6,9 1,5,9 1,5,6,9 1,2,7,9 1,2,3,9
Шаг 7: 8,9 7,8,9 5,6,8,9 4,9 4,7,9 4,5,6,9 3,8,9 3,4,9 1,9
1,7,9 1,5,6,9 1,2,9 1,2,7,9 1,2,3,9
Шаг 5:
Шаг 8: 7,9 7,8 5,6,9 5,6,8 4,7,9 4,5,6,9 3,9 3,8 3,4,9
1,5,6,9 1,2,7,9 1,2,3,9
77
76.
Решение задачи 11Максимальная группировка: 1 7,8
2 5,6,8
3 4,7,9
4 4,5,6,9
5 3,8
6 3,4,9
7 1,5,6,9
8 1,2,7,9
9 1,2,3,9
Множество состояний покрывающего автомата Sʹ:
Q 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9
78
77.
Решение задачи 11Найдем значения функции переходов:
q1 i1 , q2 i2 : a j , q1 q2 a j ,i1 i2
Например:
1 7,8
a,7 1
a,8 5
1 7 ,1 8 ,1 9
5 2 ,5 4 ,5 7
b,7 4 4 3 ,4 4 ,4 6
b,8
a,1 7
b,1 3
79
78.
Решение задачи 112 5,6,8
a,5
a,6
a,8 5
a,2 2
5 2 ,5 4 ,5 7
b,5 6 6 2 ,6 4 ,6 7
b,6
b,2 2
b,8
80
79.
Решение задачи 113 4,7,9
a,4 5
a,7 1
5 2 ,5 4 ,5 7
1 7 ,1 8 ,1 9
a,3 7
a,9
b,4
b,7 4 4 3 ,4 4 ,4 6
b,9 6 6 2 ,6 4 ,6 7
b,3 4
81
80.
Решение задачи 114 4,5,6,9
a,4 5 5 2 ,5 4 ,5 7
a,5
a,4 2
a,6
a,9
b,4
b,5 6
b,6
6 2 ,6 4 ,6 7
b,4 2
b,9 6
82
81.
Решение задачи 115 3,8
a,3
a,8 5
5 2 ,5 4 ,5 7
b,3 1
1 7 ,1 8 ,1 9
b,8
a,5 2
b,5 7
83
82.
Решение задачи 116 3,4,9
a,3
a,4 5
a,9
5 2 ,5 4 ,5 7
a,6 2
b,3 1 1 7 ,1 8 ,1 9
b,4
b,6 7
b,9 6 6 2 ,6 4 ,6 7
84
83.
Решение задачи 117 1,5,6,9
a,1 2
a,5
a,6
a,9
b,1
b,5 6
b,6
b,9 6
2 8 ,2 9
a,7 8
6 2 ,6 4 ,6 7
b,7 2
85
84.
Решение задачи 118 1,2,7,9
a,1 2
a,2 3
a,7 1
a,9
b,1
b,2
b,7 4
b,9 6
2 8 ,2 9
3 5 ,3 6 ,3 9
1 7 ,1 8 ,1 9
4 3 ,4 4 ,4 6
a,8 9
b,8 4
6 2 ,6 4 ,6 7
86
85.
Решение задачи 119 1,2,3,9
a,1 2
a,2 3
a,3
a,9
b,1
b,2
b,3 1
b,9 6
2 8 ,2 9
3 5 ,3 6 ,3 9
1 7 ,1 8 ,1 9
6 2 ,6 4 ,6 7
a,9 9
b,9 7
87
86.
Решение задачи 11Найдем значения функции выхода:
q1 i : a j , q1 ak a j ,i ak
Например: 1 7,8
a,1 a,7 a,8 y
b,1 b,7 y
2 5,6,8
a,2 a,5 a,6 a,8 y
b,2 b,5 x
88
87.
Решение задачи 113 4,7,9
a,3 a,4 x
b,3 b,4 b,7 y
4 4,5,6,9 a,4 a,4 x
b,4 b,4 b,5 x
5 3,8
a,5 a,3 a,8 y
b,5 b,3 y
6 3,4,9
a,6 a,3 a,4 x
b,6 b,3 y
89
88.
Решение задачи 117 1,5,6,9
a,7 a,1 a,5 a,6 a,9 x
b,7 b,1 b,5 x
8 1,2,7,9
a,8 a,1 a,2 x
b,8 b,1 b,2 y
9 1,2,3,9
a,9 a,1 a,2 x
b,9 b,1 b,2 y
90
89.
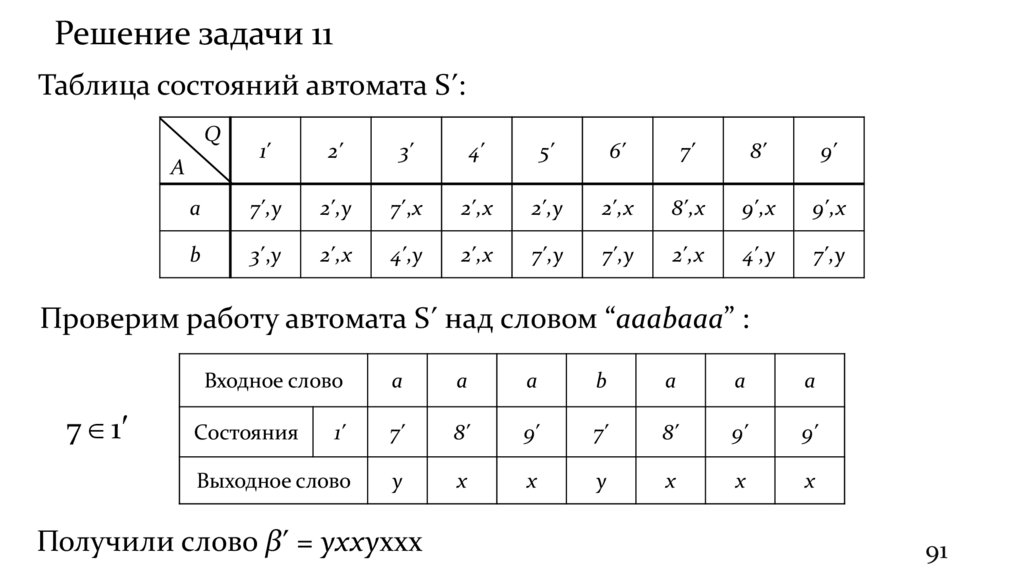
Решение задачи 11Таблица состояний автомата Sʹ:
Q
1ʹ
2ʹ
3ʹ
4ʹ
5ʹ
6ʹ
7ʹ
8ʹ
9ʹ
a
7ʹ,y
2ʹ,y
7ʹ,x
2ʹ,x
2ʹ,y
2ʹ,x
8ʹ,x
9ʹ,x
9ʹ,x
b
3ʹ,y
2ʹ,x
4ʹ,y
2ʹ,x
7ʹ,y
7ʹ,y
2ʹ,x
4ʹ,y
7ʹ,y
A
Проверим работу автомата Sʹ над словом “aaabaaa” :
7 1
Входное слово
a
a
a
b
a
a
a
Состояния
1ʹ
7ʹ
8ʹ
9ʹ
7ʹ
8ʹ
9ʹ
9ʹ
Выходное слово
y
x
x
y
x
x
x
Получили слово βʹ = yxxyxxx
91
90.
Решение задачи 113. Построим покрывающий автомат с применением Т-алгоритма.
Выписать все состояния автомата
Вычеркнуть все состояния, несовместимые с первым
состоянием в строке
Строчкой ниже переписать все оставшиеся состояния, и
повторить предыдущий пункт
Повторять предыдущие пункты, проходясь по всем
состояниям
Собрать группу совместимости
Выписать все оставшиеся состояния автомата, и повторить все
пункты
92
91.
Решение задачи 111
2
3 4 5 6 7 8 9
2
3
3
5 6 7
7
1 1,2,3,9
9
9
9
4 5 6 7 8
7 8
5 6 7
6
2 4,5,6
3 7,8
93
92.
Решение задачи 11Проверим полученную группировку на замкнутость:
q1 , q2 Q1 : ai , q1 Q2 ai , q2 Q2
Например: 1 1,2,3,9
a,1 2
a,2 3
a,3
a,9
2 1
3 1
a,1 1
Добавим новое состояние:
b,1
b,2
b,3 1 1 1
b,9 6 6 2
4 1,6 b,1 4
94
93.
Решение задачи 112 4,5,6
a,4 5 5 2
a,5
a,2 2
a,6
b,4
b,5 6 6 2 b,2 2
b,6
3 7,8
b,7 4 4 2
b,3 2
b,8
a,7 1 1 1
a,8 5 5 2
Отметим, что 5 совместимо с 1 и 6
Добавим 5 в состояние: 4 1,5,6
a,3 4
95
94.
Решение задачи 114 1,5,6
b,1
a,1 2 2 1
a,5
a,4 1 b,5 6 6 2 b,4 2
a,6
b,6
Множество состояний покрывающего автомата Sʹʹ:
Q 1 ,2 ,3 ,4
96
95.
Решение задачи 11Найдем значения функции выхода:
1 1,2,3,9 a,1 a,1 a,2 x
b,1 b,1 b,2 y
2 4,5,6
a,2 a,4 x
b,2 b,4 b,5 x
3 7,8
a,3 a,7 a,8 y
b,3 b,7 y
4 1,5,6
a,4 a,1 a,5 a,6
b,4 b,1 b,5 x
97
96.
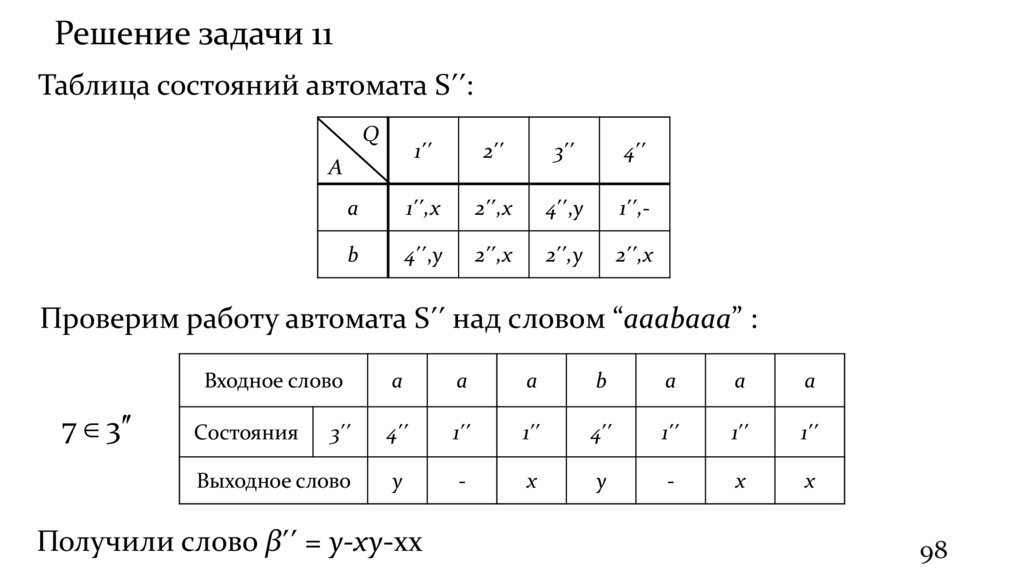
Решение задачи 11Таблица состояний автомата Sʹʹ:
Q
1ʹʹ
2ʹʹ
3ʹʹ
4ʹʹ
a
1ʹʹ,x
2ʹʹ,x
4ʹʹ,y
1ʹʹ,-
b
4ʹʹ,y
2ʹʹ,x
2ʹʹ,y
2ʹʹ,x
A
Проверим работу автомата Sʹʹ над словом “aaabaaa” :
7 3
Входное слово
a
a
a
b
a
a
a
Состояния
3ʹʹ
4ʹʹ
1ʹʹ
1ʹʹ
4ʹʹ
1ʹʹ
1ʹʹ
1ʹʹ
Выходное слово
y
-
x
y
-
x
x
Получили слово βʹʹ = y-xy-xx
98
97.
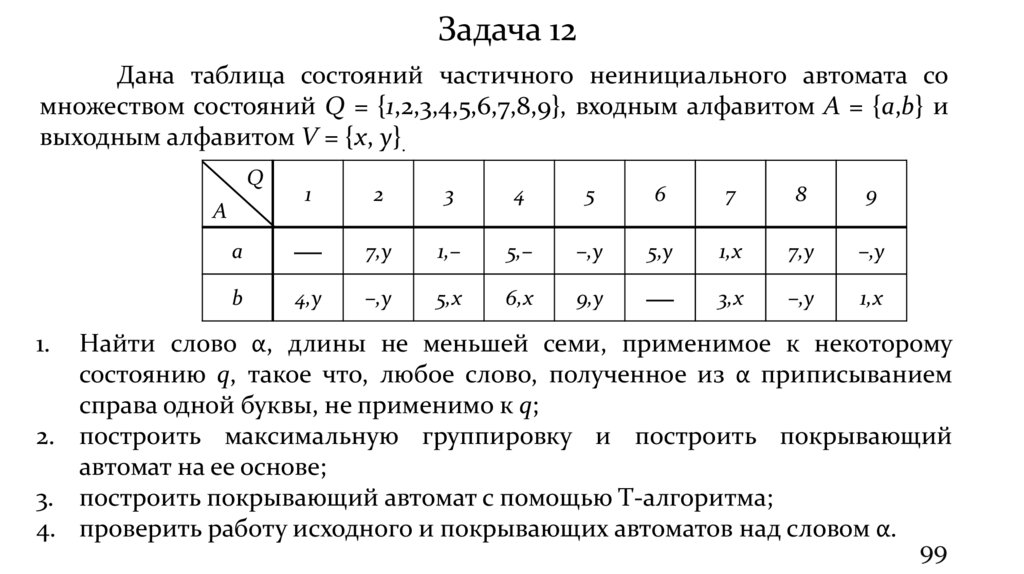
Задача 12Дана таблица состояний частичного неинициального автомата со
множеством состояний Q = {1,2,3,4,5,6,7,8,9}, входным алфавитом A = {a,b} и
выходным алфавитом V = {x, y}.
Q
1
2
3
4
5
6
7
8
9
a
—
7,y
1,–
5,–
–,y
5,y
1,x
7,y
–,y
b
4,y
–,y
5,x
6,x
9,y
—
3,x
–,y
1,x
A
1.
Найти слово α, длины не меньшей семи, применимое к некоторому
состоянию q, такое что, любое слово, полученное из α приписыванием
справа одной буквы, не применимо к q;
2. построить максимальную группировку и построить покрывающий
автомат на ее основе;
3. построить покрывающий автомат с помощью Т-алгоритма;
4. проверить работу исходного и покрывающих автоматов над словом α.
99
98.
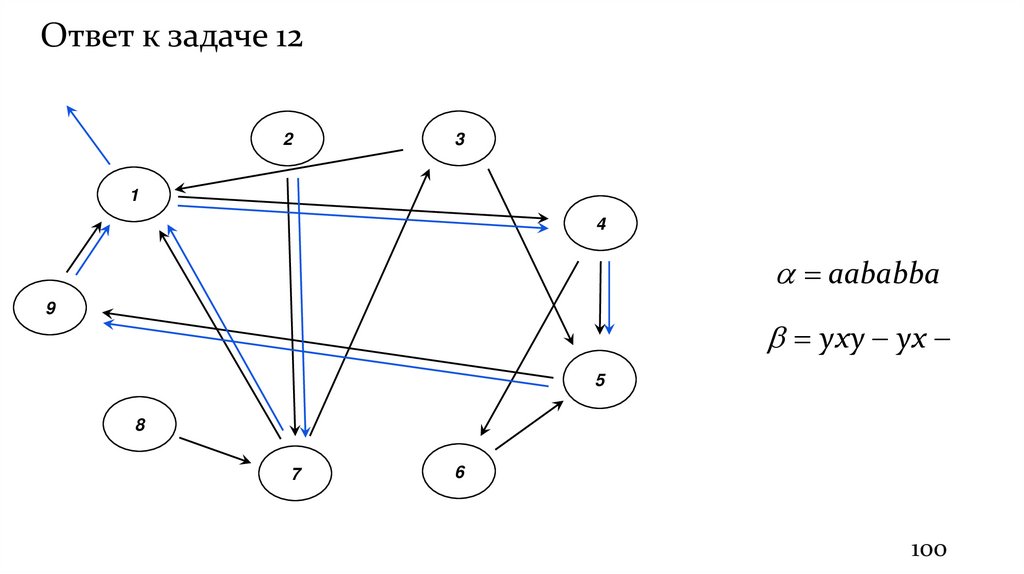
Ответ к задаче 122
3
1
4
aababba
9
yxy yx
5
8
7
6
100
99.
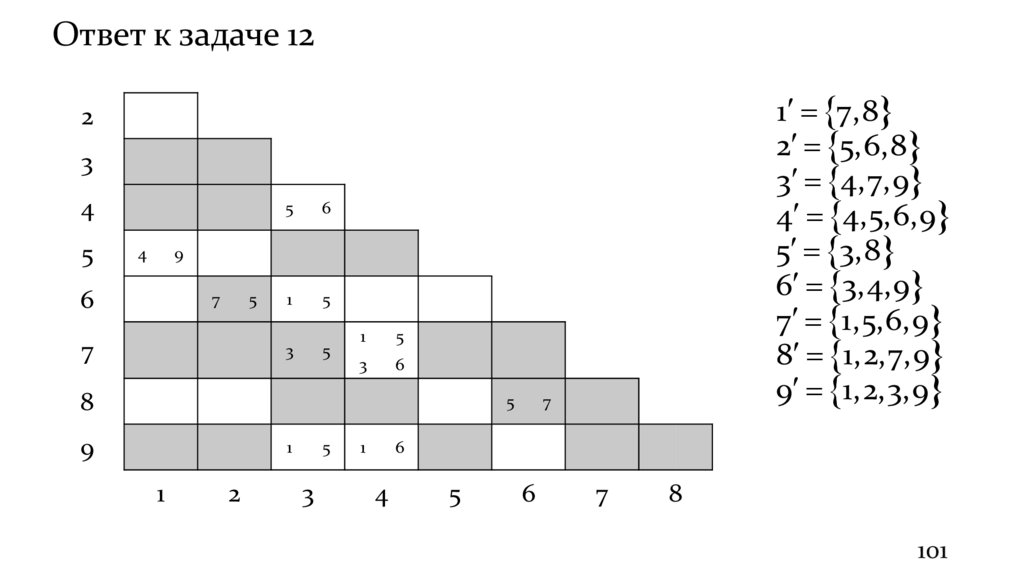
Ответ к задаче 121 7,8
2 5,6,8
3 4,7,9
4 4,5,6,9
5 3,8
6 3,4,9
7 1,5,6,9
8 1,2,7,9
9 1,2,3,9
2
3
4
5
4
5
6
1
5
3
5
9
6
7
5
7
1
5
3
6
8
5
9
1
1
2
5
3
1
7
6
4
5
6
7
8
101
100.
Ответ к задаче 121 7
2 1,5,6
3 1,2,5,8
4 3,4,6,9
Q
1ʹ
2ʹ
3ʹ
4ʹ
a
2ʹ,x
2ʹ,y
1ʹ,y
2ʹ,y
b
4ʹ,x
4ʹ,y
4ʹ,y
2ʹ,x
A
yxyyyxy
102
101.
Ответ к задаче 121 1,2,5,8
2 3,4,6,9
3 7
4 1,5,6
Q
1ʹʹ
2ʹʹ
3ʹʹ
4ʹʹ
a
3ʹʹ,y
1ʹʹ,y
1ʹʹ,x
1ʹʹ,y
b
2ʹʹ,y
4ʹʹ,x
2ʹʹ,x
2ʹʹ,y
A
yxyyyxy
103
102.
Задача 13Даны два слова α = abccbbbac, β = uupuppupp.
1.
Построить таблицы состояний автомата, осуществляющего автоматное
отображения α в β;
2. провести
минимизацию,
построить
таблицу
состояний
минимизированного автомата;
3. проверить работу полученного автомата над словом α.
104
103.
Решение задачи 131. Построим автомат, осуществляющий автоматное отображение:
Найдем входной алфавит автомата:
abccbbbac
A a, b, c
Найдем выходной алфавит автомата:
uupuppupp
V u, p
Найдем множество внутренних состояний:
9 Q 9 Q 1,2,3,4,5,6,7,8,9
105
104.
Решение задачи 13Зададим функцию переходов:
k 1,если x 1 x2 xk начало слова
xk , k
неопределена, во всех остальных случаях
abccbbbac
a,1 2
b,1
c,1
a,2
b,2 3
c,2
a,6
b,6 7
c,6
a,3
b,3
c,3 4
a,7
b,7 8
c,7
a,4
b,4
c,4 5
a,8 9
b,8
c,8
a,5
b,5 6
c,5
a,9
b,9
c,9
106
105.
Решение задачи 13Зададим функцию выходов:
yk ,если x 1 x2 xk начало слова , yk k -й символ
xk , k
неопределена, во всех остальных случаях
abccbbbac
a,1 u
b,1
c,1
a,2
b,2 u
c,2
a,6
b,6 p
c,6
a,3
b,3
c,3 p
a,7
b,7 u
c,7
a,4
b,4
c,4 u
a,8 p
b,8
c,8
a,5
b,5 p
c,5
a,9
b,9
c,9 p
107
106.
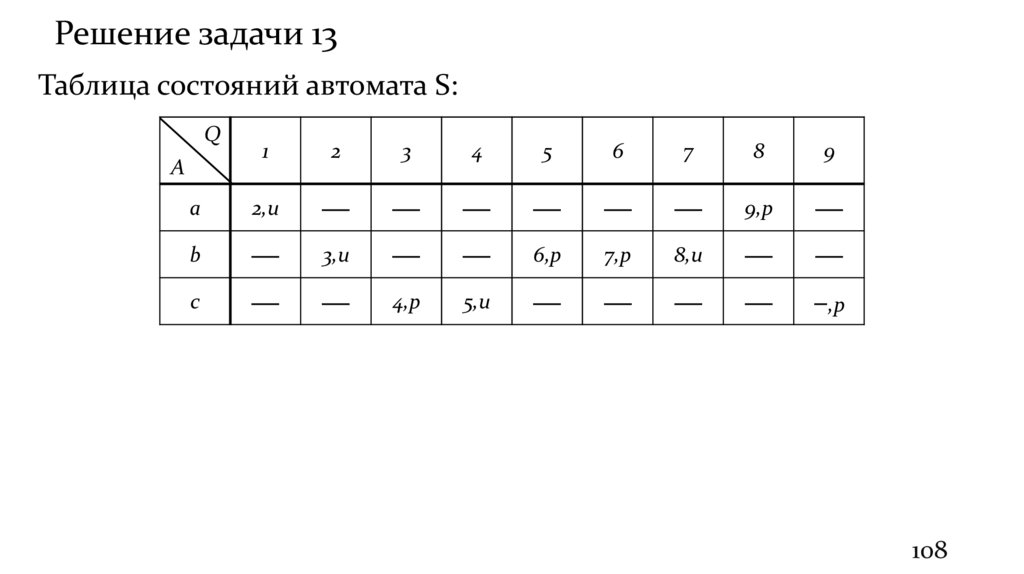
Решение задачи 13Таблица состояний автомата S:
Q
1
2
3
4
5
6
7
8
9
a
2,u
—
—
—
—
—
—
9,p
—
b
—
3,u
—
—
6,p
7,p
8,u
—
—
с
—
—
4,p
5,u
—
—
—
—
–,p
A
108
107.
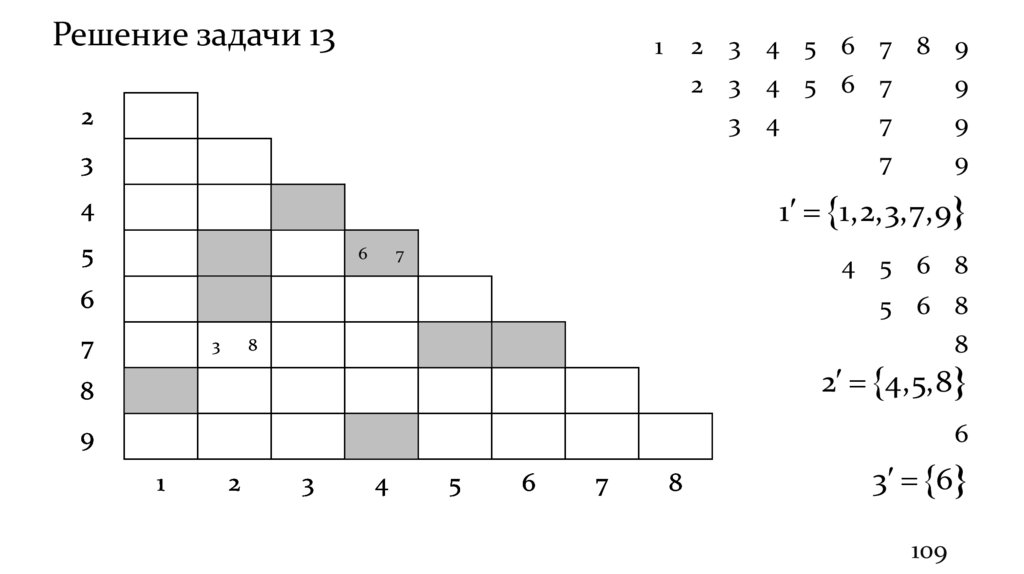
Решение задачи 131
2
2
2
3 4 5 6 7 8 9
3 4 5 6 7
9
3 4
3
7
7
4
1 1,2,3,7,9
5
6
7
4 5 6 8
6
7
3
9
9
5 6 8
8
8
8
2 4,5,8
9
6
1
2
3
4
5
6
7
8
3 6
109
108.
Решение задачи 13Проверим полученную группировку на замкнутость:
1 1,2,3,7,9
a,1 2 1
b,1
a,2
b,2 3 1
a,3 a,1 1 b,3
a,7
b,7 8 2
a,9
b,9
c,1
c,2
c,3 4 2 c,1 2
c,7
c,9
3 и 8 совместимы с 6 3 3,6,8 b,1 3
110
109.
Решение задачи 132 4,5,8
a,4
a
,2
1
a
,5
a,8 9 1
b,4
b,5 6 3 b,2 3
b,8
c,4 5 2
c,2 2
c,5
c,8
3 3,6,8
a,3
a
,3
1
a
,6
a,8 9 1
b,3
b,6 7 1 b,3 1
b,8
c,3 4 2
c,3 2
c,6
c,8
111
110.
Решение задачи 13Найдем значения функции выхода:
1 1,2,3,7,9
2 4,5,8
3 3,6,8
a,1 a,1 u
b,1 b,2 u
c,1 c,3 p
a,2 a,8 p
b,2 b,5 p
c,2 c,4 u
a,3 a,8 p
b,3 b,6 p
c,3 c,3 p
112
111.
Решение задачи 13Q
1ʹ
2ʹ
3ʹ
a
1ʹ,u
1ʹ,p
1ʹ,p
b
3ʹ,u
3ʹ,p
1ʹ,p
c
2ʹ,p
2ʹ,u
2ʹ,p
A
Проверим работу автомата Sʹ над словом “abccbbbac” :
1 1
Входное слово
a
b
c
c
b
b
b
a
c
Состояния
1ʹ
1ʹ
3ʹ
2ʹ
2ʹ
3ʹ
1ʹ
3ʹ
1ʹ
2ʹ
Выходное слово
u
u
p
u
p
p
u
p
p
Получили слово βʹ = uupuppupp = β.
113
112.
Задача 14Даны два слова α = bacaabacb, β = upuppuppu.
1.
Построить таблицы состояний автомата, осуществляющего автоматное
отображения α в β;
2. провести
минимизацию,
построить
таблицу
состояний
минимизированного автомата;
3. проверить работу полученного автомата над словом α.
114
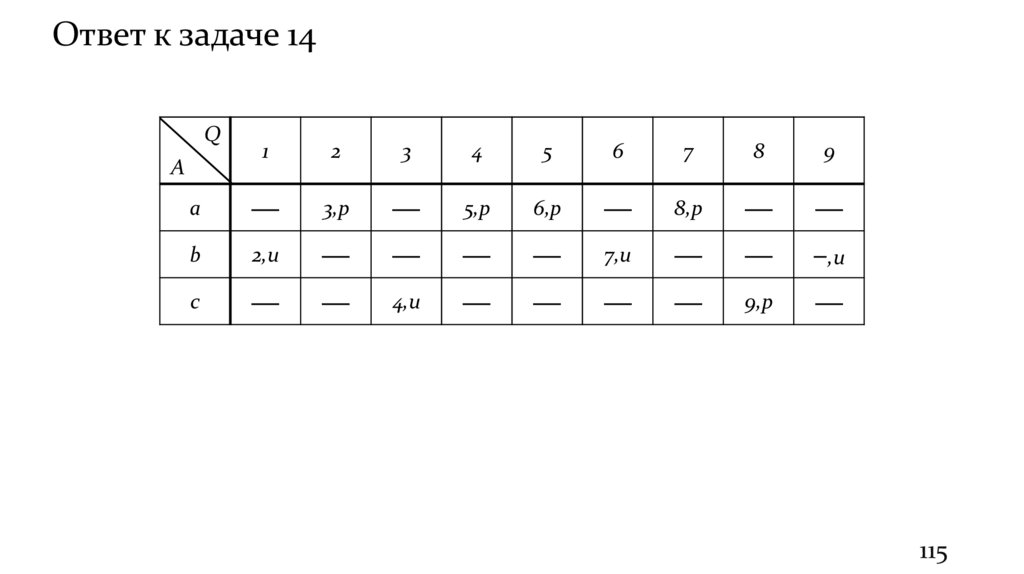
113.
Ответ к задаче 14Q
1
2
3
4
5
6
7
8
9
a
—
3,p
—
5,p
6,p
—
8,p
—
—
b
2,u
—
—
—
—
7,u
—
—
–,u
с
—
—
4,u
—
—
—
—
9,p
—
A
115
114.
Ответ к задаче 142
1 1,2,3,4,5,9
2 6,7,8
3
4
3
5
5
3
6
5
6
3
8
5
8
6
2
7
7
6
8
8
9
1
2
3
4
5
6
7
8
116
115.
Ответ к задаче 141 1,2,3,4,5,9
2 6,7,8
3 3,5,6
Q
1ʹ
2ʹ
3ʹ
a
3ʹ,p
2ʹ,p
2ʹ,p
b
1ʹ,u
2ʹ,u
2ʹ,u
c
1ʹ,u
1ʹ,p
1ʹ,u
A
upuppuppu
117
116.
117.
Автомат МураОпределение: автоматом Мура называется пятерка объектов
Q, A, V, , µ = S, такая что
Q – множество внутренних состояний;
A – входной алфавит;
V – выходной алфавит;
: Q A Q – функция переходов;
µ : Q V – функция отметок.
Таблица, задающая функции переходов и отметок, называется
таблицей состояний автомата.
119
118.
Автомат без выходаОпределение: автоматом без выхода называется
объектов Q, A, F, q1, = S, такая что
Q – множество внутренних состояний;
A – входной алфавит;
F Q – множество конечных состояний;
q1 Q – начальное состояние.
: Q A Q – функция переходов.
пятерка
120
119.
СобытияОпределение: событием называется множество E, что E A*, где
A* – множество слов в алфавите А.
Определение: элементарным событием называется слово,
состоящее из одной буквы.
Определение: событие Е представимо автоматом без выхода S,
если автомат при работе над словом α переходит в одно из своих
заключительных состояний тогда и только тогда, когда α E.
121
120.
Операции над событиямиОпределение: конкатенацией событий Е1 и Е2 называется
событие Е1°Е2:
E 1 E2 1 2 1 E 1 и 2 E2
Определение: итерацией события Е называется событие Е*:
E * e E EE E 3
где е – пустое слово, E k E E
Ek ,
E – регулярная степень.
k раз
Определение: событие называется регулярным, если оно
может быть получено из элементарных событий с помощью
применения конечного числа раз операций конкатенации,
объединения и итерации.
122
121.
ИсточникОпределение: источником называется ориентированный граф,
в котором:
1. выделено некоторое множество начальных вершин и
некоторое множество конечных вершин, имеющих, возможно,
непустое пересечение;
2. над каждым ребром графа стоит или буква из входного
алфавита, или пустое слово.
Определение: исток – вершина, из которой ребра только
выходят, сток – вершина, в которую ребра только заходят.
123
122.
Детерминированный источникОпределение: источник H представляет событие E, если Е
состоит из тех и только тех слов, которые соответствуют всем
маршрутам из начальных вершин источника в заключительные
вершины.
Определение: источник называется детерминированным, если
он содержит только одну начальную вершину, не имеет пустых
ребер, и для любой вершины h источника и любого символа а
входного алфавита существует единственное ребро, выходящее
из вершины h и помеченная символом a.
124
123.
Недетерминированный автоматОпределение: недетерминированным автоматом называется
пятерка объектов Q, A, F, q1, Н = S, такая что
Q – множество внутренних состояний;
A – входной алфавит;
F – множество конечных состояний;
q1 – начальное состояние.
Н : Q A P(Q) – функция переходов, где P(Q) – множество всех
подмножеств множества Q.
125
124.
125.
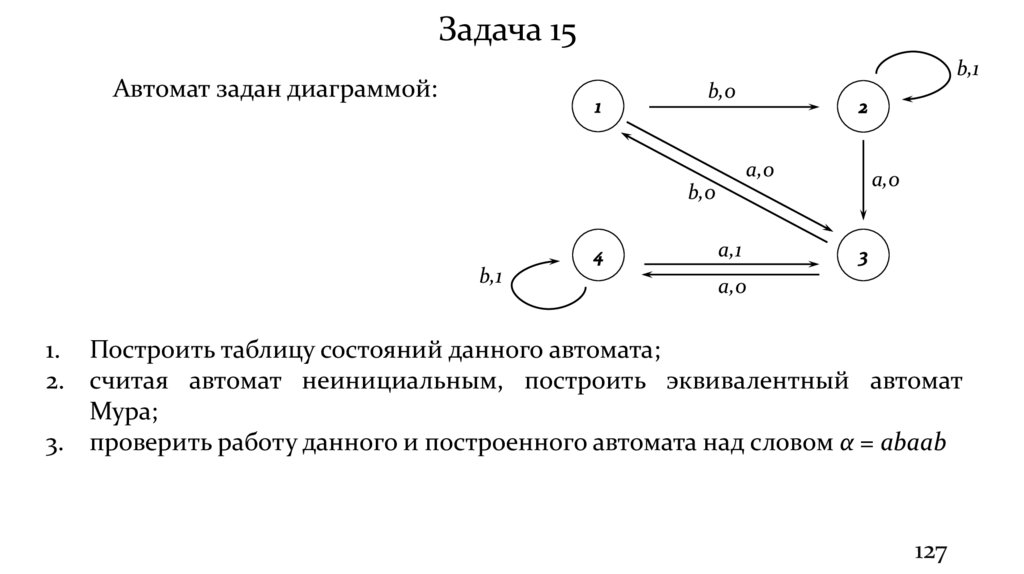
Задача 15b,1
Автомат задан диаграммой:
b,0
a,0
b,0
a,0
a,1
b,1
a,0
1. Построить таблицу состояний данного автомата;
2. считая автомат неинициальным, построить эквивалентный автомат
Мура;
3. проверить работу данного и построенного автомата над словом α = abaab
127
126.
Решение задачи 15Построим таблицу состояний автомата:
Q
A a, b
V 0,1
1
2
3
4
a
3,0
3,0
4,0
3,1
b
2,0
2,1
1,0
4,1
A
Q 1,2,3,4
Проверим работу автомата S над словом α = abaab:
Входное слово
a
b
a
a
b
Состояния
1
3
1
3
4
4
Выходное слово
0
0
0
0
1
Получили слово β = 00001.
128
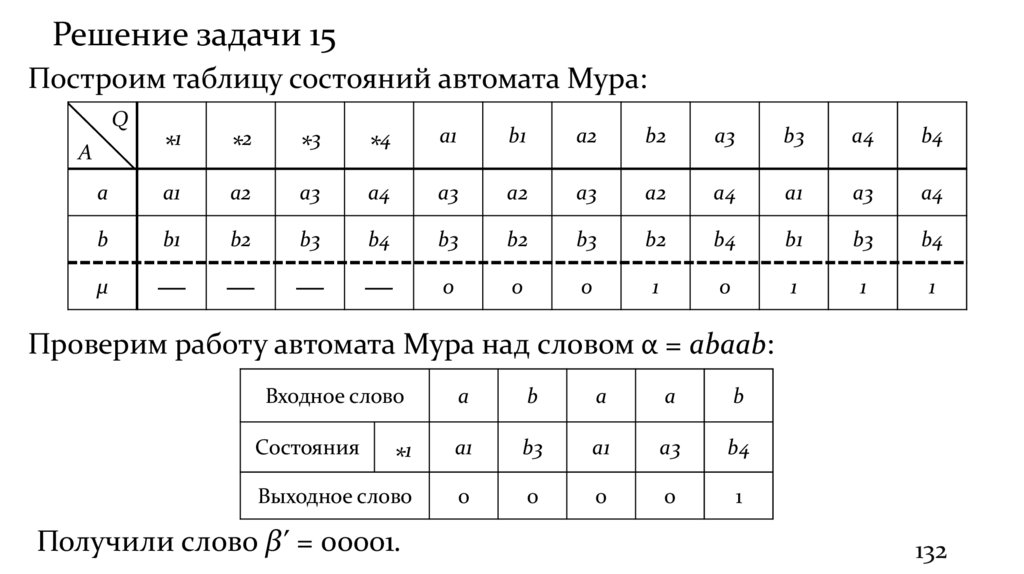
127.
Решение задачи 15Построим эквивалентный автомат Мура:
Определим количество внутренних состояний:
Q A 1 Q 2 1 4 12
К внешнему алфавиту добавляется некоторый неизвестный
символ – .
* Q 1, 2, 3, 4, a1, b1, a2, b2, a3, b3, a4, b4
129
128.
Решение задачи 15Построим функцию переходов:
x A x , yii xi
xj,,i j 1..
Qy,i , y A,i 1.. Q
a, 1 a1 aa,, a21 a23 a, 3 a3 aa, , b41 aa42
a,1 3
b,1 2
b, 1 b1 bb,, a21 b23 b, 3 b3 bb, , b41 bb42
a, b2 a2
a, a2 a3
a,2 3
b,2 2
b, b2 b2
b, a2 b3
a, b3 a1
a, a3 a4
a,3 4
b,3 1
b, b3 b1
b, a3 b4
a, b4 a4
a, a4 a3
a,4 3
b,4 4
b, b4 b4
b, a4 b3
130
129.
Решение задачи 15Построим функцию отметок:
i неопределена, i 1.. Q
1 2 3 4
xi x ,i , x A,i 1.. Q
a1 a,1 0
b1 b,1 0
a2 a,2 0
b2 b,2 1
a3 a,3 0
b3 b,3 1
a4 a,4 1
b4 b,4 1
131
130.
Решение задачи 15Построим таблицу состояний автомата Мура:
Q
*1
*2
*3
*4
a1
b1
a2
b2
a3
b3
a4
b4
a
a1
a2
a3
a4
a3
a2
a3
a2
a4
a1
a3
a4
b
b1
b2
b3
b4
b3
b2
b3
b2
b4
b1
b3
b4
μ
—
—
—
—
0
0
0
1
0
1
1
1
A
Проверим работу автомата Мура над словом α = abaab:
Входное слово
a
b
a
a
b
Состояния
*1
a1
b3
a1
a3
b4
Выходное слово
0
0
0
0
1
Получили слово βʹ = 00001.
132
131.
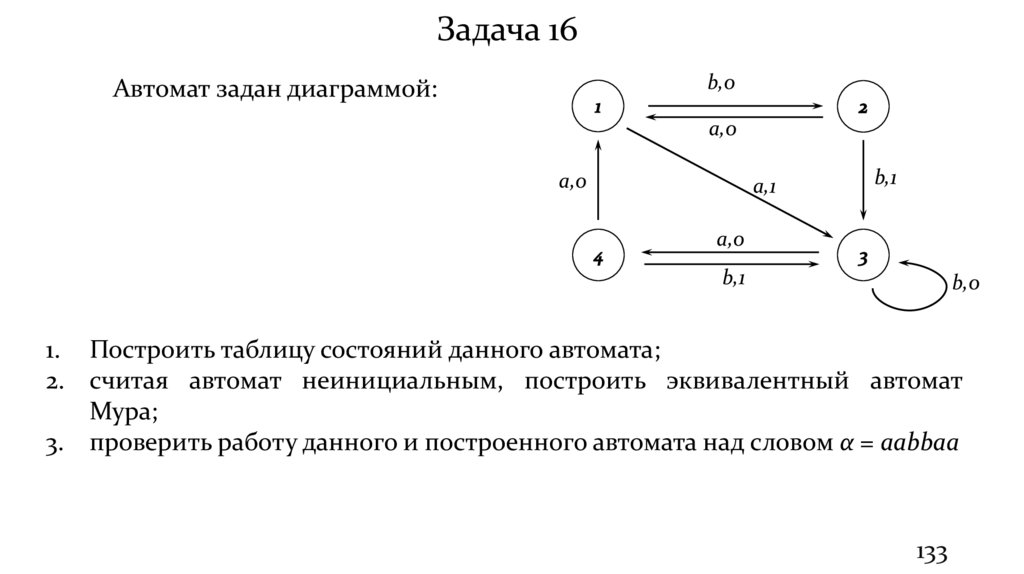
Задача 16b,0
Автомат задан диаграммой:
a,0
a,0
a,1
b,1
a,0
b,1
b,0
1. Построить таблицу состояний данного автомата;
2. считая автомат неинициальным, построить эквивалентный автомат
Мура;
3. проверить работу данного и построенного автомата над словом α = aabbaa
133
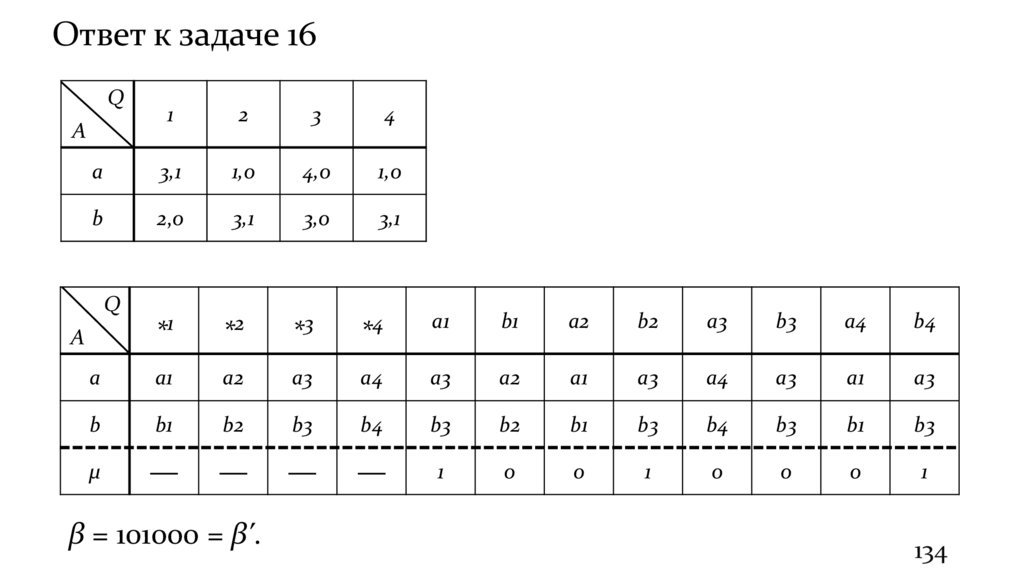
132.
Ответ к задаче 16Q
1
2
3
4
a
3,1
1,0
4,0
1,0
b
2,0
3,1
3,0
3,1
*1
*2
*3
*4
a1
b1
a2
b2
a3
b3
a4
b4
a
a1
a2
a3
a4
a3
a2
a1
a3
a4
a3
a1
a3
b
b1
b2
b3
b4
b3
b2
b1
b3
b4
b3
b1
b3
μ
—
—
—
—
1
0
0
1
0
0
0
1
A
Q
A
β = 101000 = βʹ.
134
133.
135134.
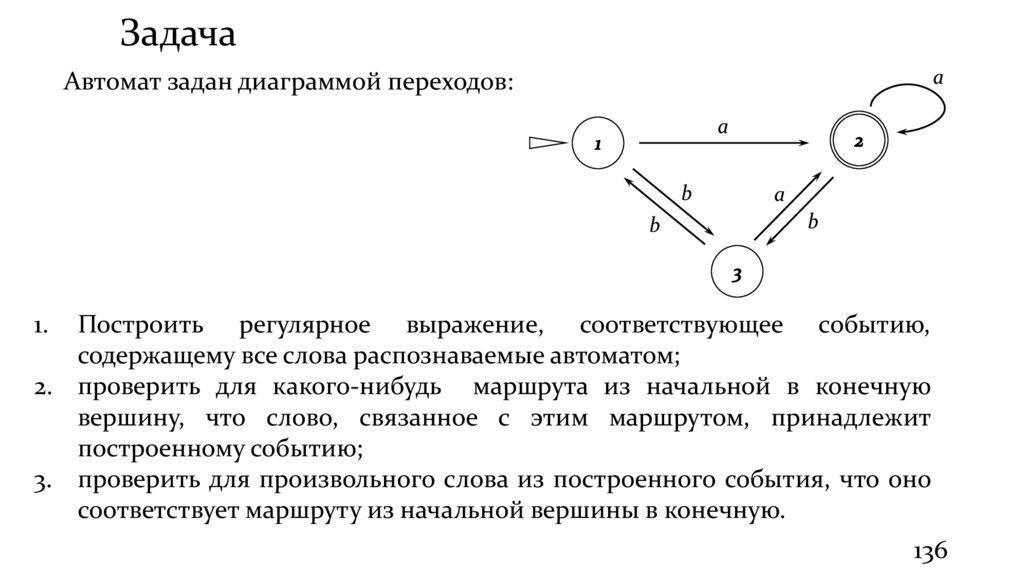
Задачаa
Автомат задан диаграммой переходов:
a
b
b
a
b
1.
Построить регулярное выражение, соответствующее событию,
содержащему все слова распознаваемые автоматом;
2. проверить для какого-нибудь маршрута из начальной в конечную
вершину, что слово, связанное с этим маршрутом, принадлежит
построенному событию;
3. проверить для произвольного слова из построенного события, что оно
соответствует маршруту из начальной вершины в конечную.
136
135.
Решение задачиУтверждение (теорема МакНатона):
Числа Eijk образуют слова, соответствующие маршрутам из i-ой
вершины в j-ю вершину, причем в этих маршрутах номера
вершин, проходимых внутри маршрута, не превосходят k.
0 шаг : Eij0 x x , qi q j
l шаг : E E
l
ij
l 1
ij
k шаг : E E
k
ij
E
k 1
ij
l 1
il
E
E
k 1
ik
l 1
E
lj ,0 l k
l 1 *
ll
E E
k 1 *
kk
l 1
kj
137
136.
Решение задачиНачальное состояние: s = 1,
множество конечных состояний: F = {2},
общее количество состояний: k = 3.
Таким образом, искомое событие для автомата: E
Найдем начальные значения:
3
12
E 110 e E 120 a E 130 b
0
0
0
E21 E22 a E23 b
0
E 310 b E 32
a E 330 e
Если остаемся в том же состоянии – ставим e – пустое слово;
если перехода нет – ставим Ø.
138
137.
Решение задачиНайдем события для l = 1:
*
1
0
0
0 *
0
При i 1, j 1 : E 11 E 11 E 11 E 11 E 11 e e e e e
*
1
0
0
0 *
0
j 2 : E 12 E 12 E 11 E 11 E 12 a e e a a a a
*
1
0
0
0 *
0
j 3 : E 13 E 13 E 11 E 11 E 13 b e e b b b b
При i 2, j 1 : E E E E E e e
*
j 2 : E E E E E a e a a
*
j 3 : E E E E E b e b b
1
21
1
22
1
23
0
21
0
22
0
23
0
21
0
21
0
21
1
31
0
31
0
31
1
32
0
32
0
31
1
33
0
33
0
31
0 *
11
0 *
11
0 *
11
0 *
*
0
11
0
12
0
13
При i 3, j 1 : E E E E 11 E b b e e b
0
11
*
0
12
*
0
13
*
j 2 : E E E E E a b e a a ba
0 *
11
0 *
j 3 : E E E E 11 E e b e b e bb
139
138.
Решение задачиПолучим выражение для события E E E E E 322
Найдем его составляющие:
*
2
1
1
1 *
1
i 1, j 2, l 2 : E 12 E 12 E 12 E22 E22 a a a a a aa*a
3
12
i 1, j 3, l 2 : E E E E
2
13
2
33
1
13
1
33
1
12
1
32
i 3, j 3, l 2 : E E E
2
12
2
13
2 *
33
*
E
b
a
a
b
b
aa
b
1 *
1
22
23
1 *
1
22
23
*
E E e bb a ba a b
*
e bb a ba a*b
*
2
1
1
1 *
1
i 3, j 2, l 2 : E 33 E 32 E 32 E22 E22 a ba a ba a a
a ba a ba a*a
Получим:
E a aa a b aa b e bb a ba a b a ba a ba a*a
3
12
*
*
*
*
140
139.
Решение задачиРассмотрим произвольный маршрут из вершины 1 в вершину 2:
1
3
1
2
3
2
b
b
a
b
a
bbaba
Проверим его наличие в полученном выражении:
E a aa a b aa b e bb a ba a b a ba a ba a*a
3
12
*
*
*
*
Рассмотрим произвольное слово из E 123 :
E a aa a b aa b e bb a ba a b a ba a ba a a
3
12
*
*
*
*
*
Проверим наличие маршрута из вершины 1 в вершину 2:
a
b
a
a
b
b
a
abaabba 1
2
3
2
2
3
1
2
141
140.
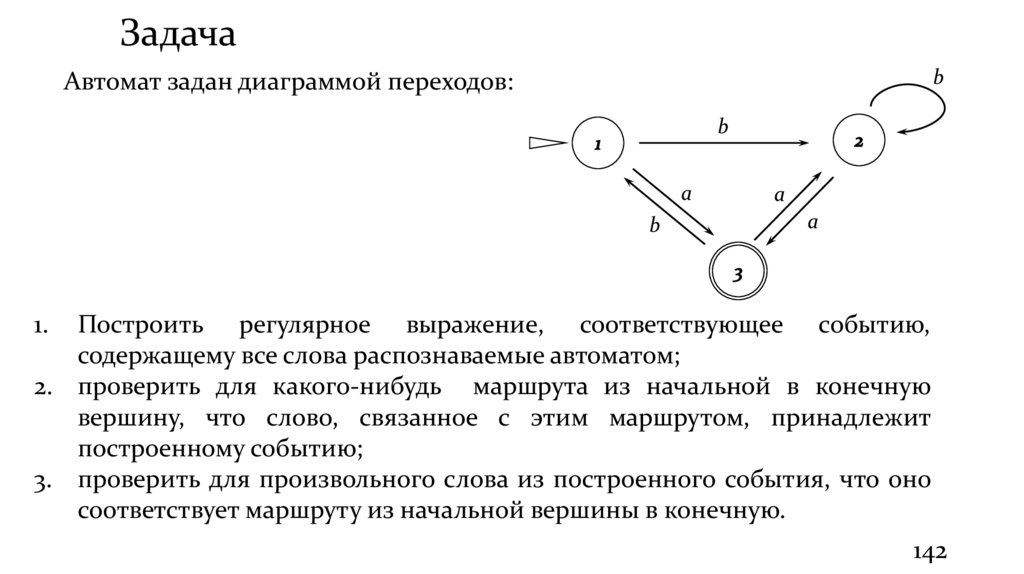
Задачаb
Автомат задан диаграммой переходов:
b
a
b
a
a
1.
Построить регулярное выражение, соответствующее событию,
содержащему все слова распознаваемые автоматом;
2. проверить для какого-нибудь маршрута из начальной в конечную
вершину, что слово, связанное с этим маршрутом, принадлежит
построенному событию;
3. проверить для произвольного слова из построенного события, что оно
соответствует маршруту из начальной вершины в конечную.
142
141.
Ответ к задачеE a bb a a bb a e ba a bb b a e ba a bb b*a
3
13
*
*
*
*
143



























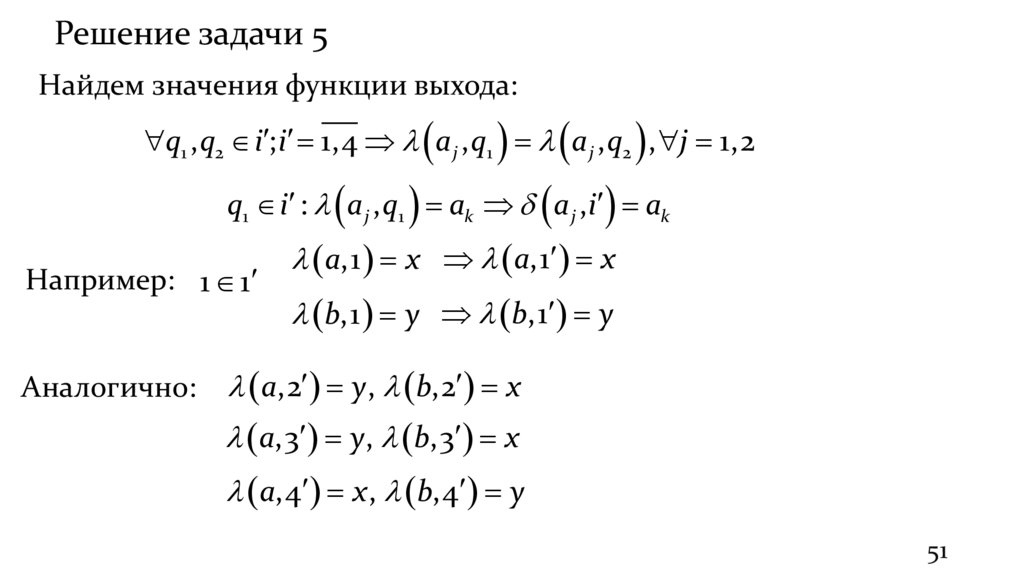




















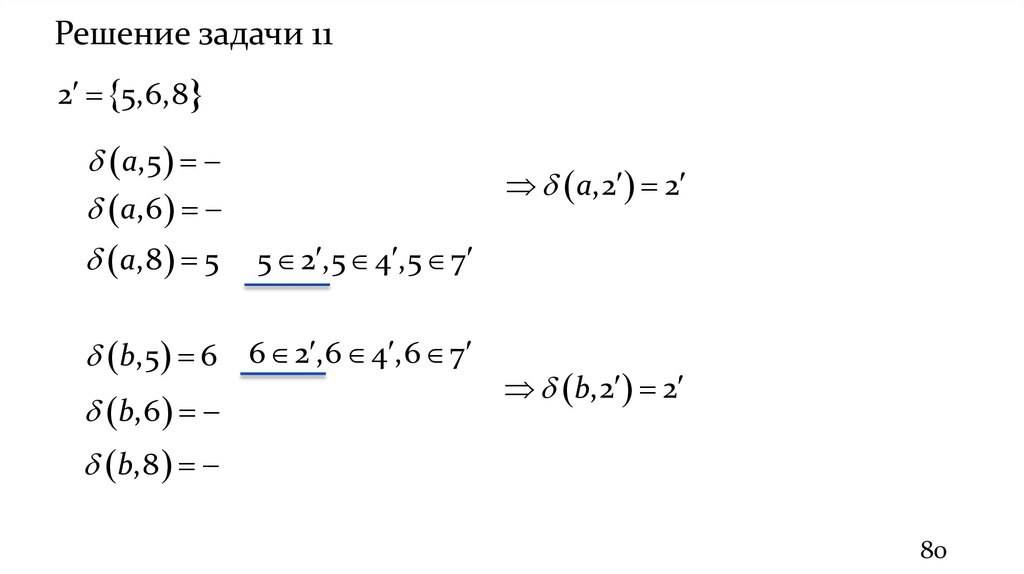
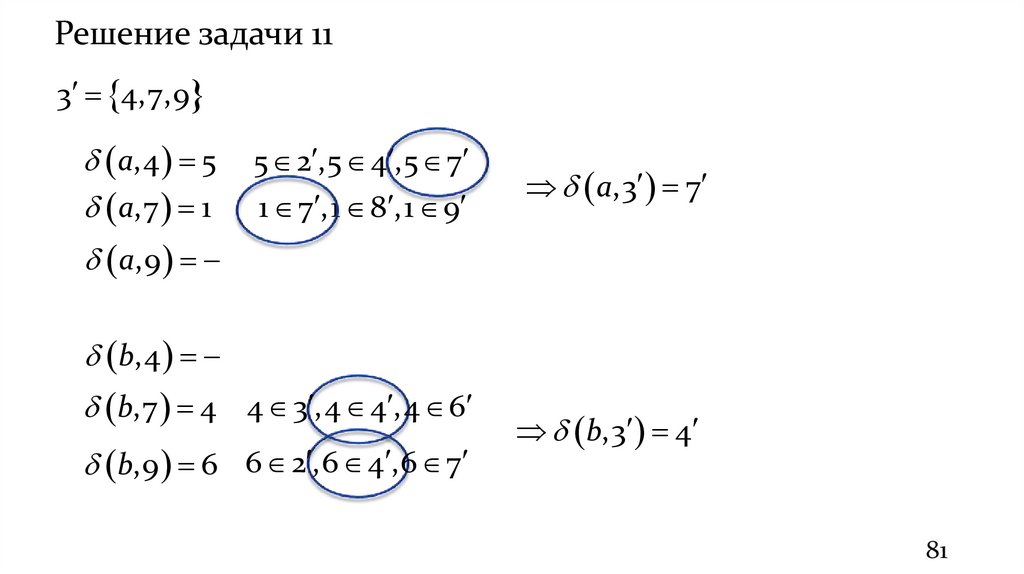
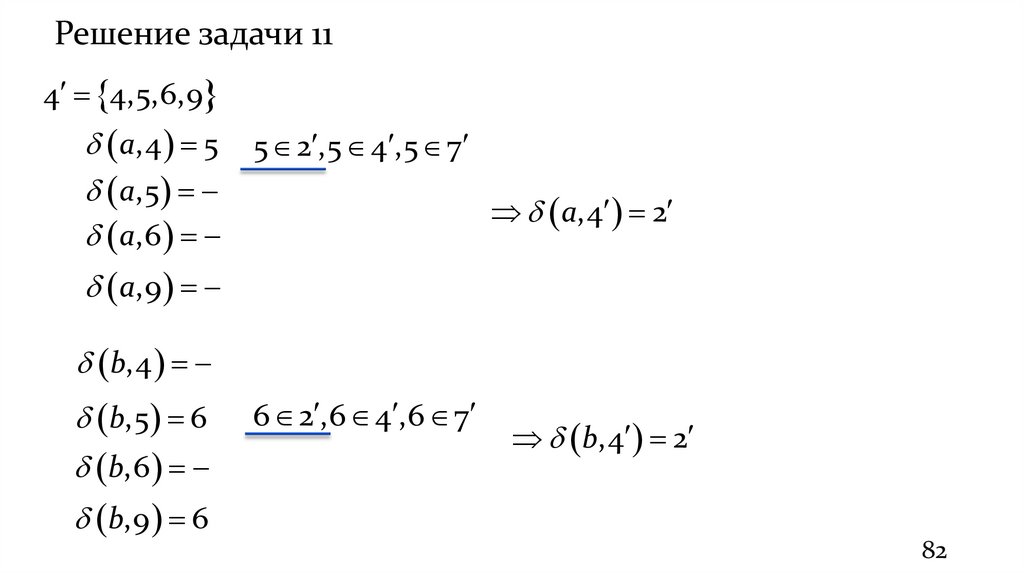
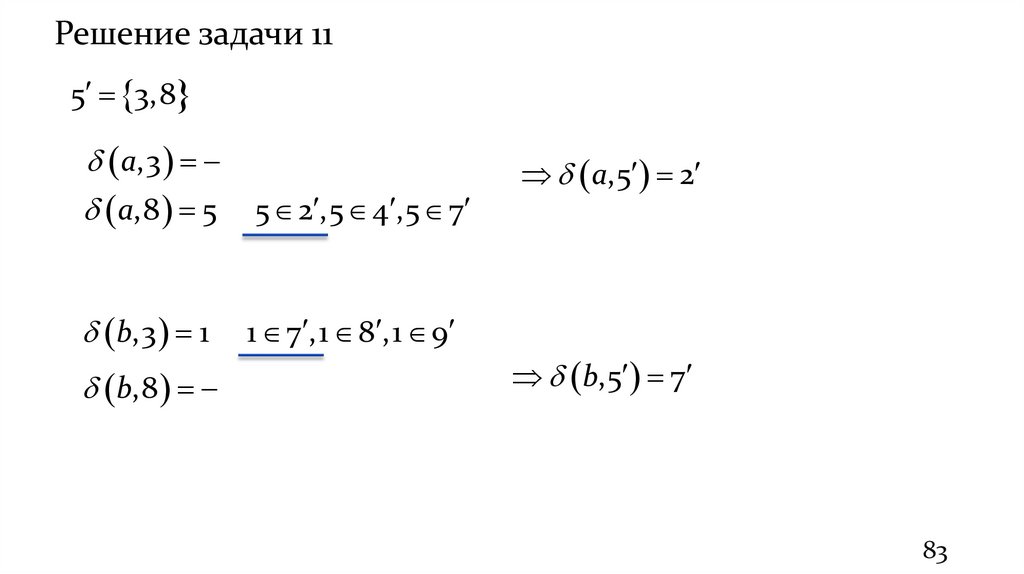
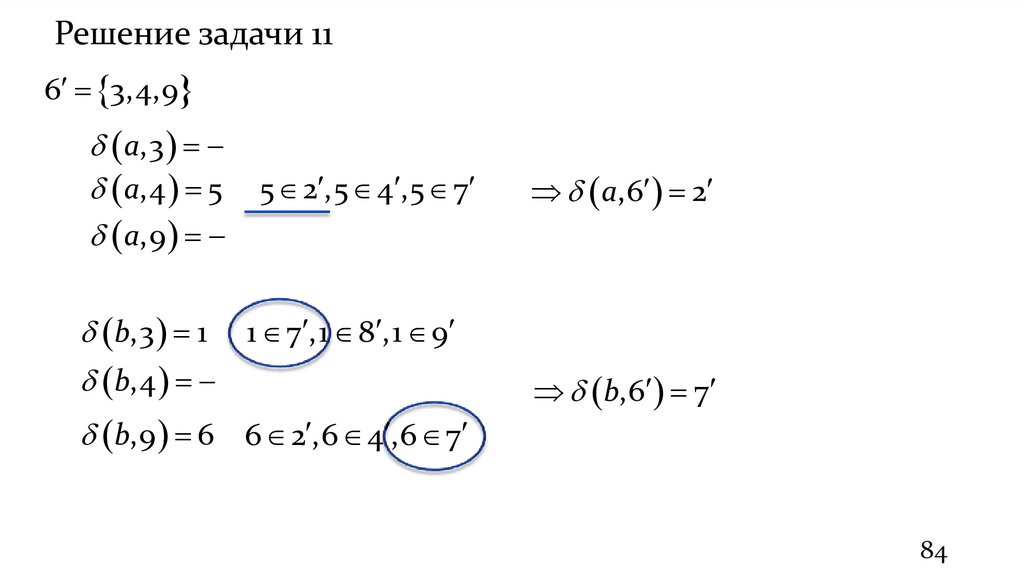
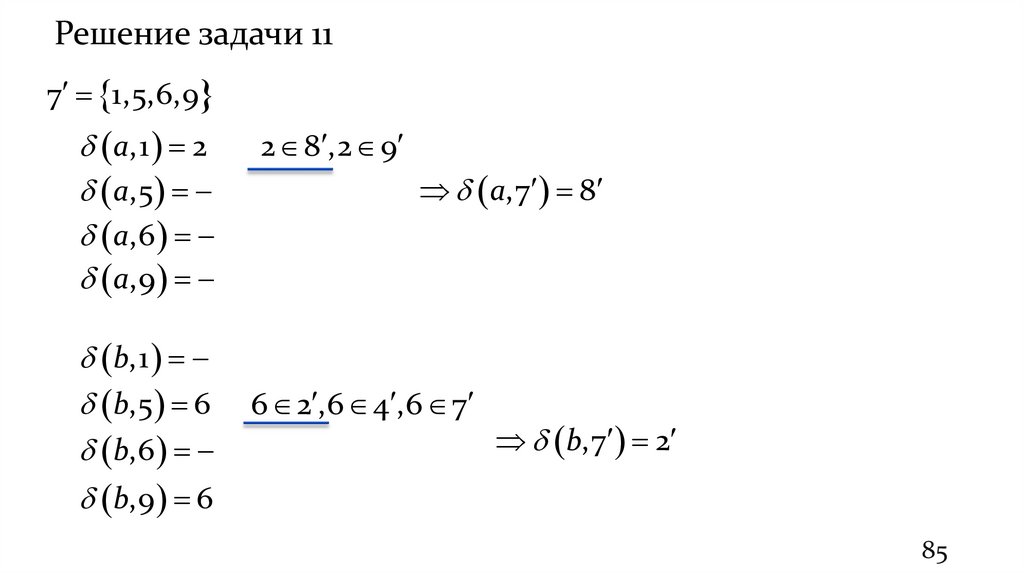
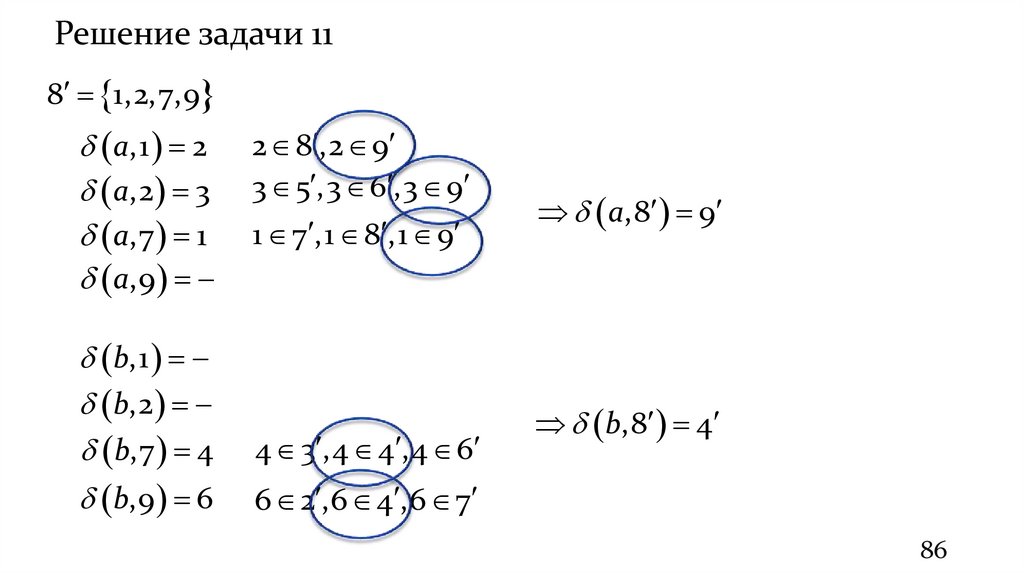
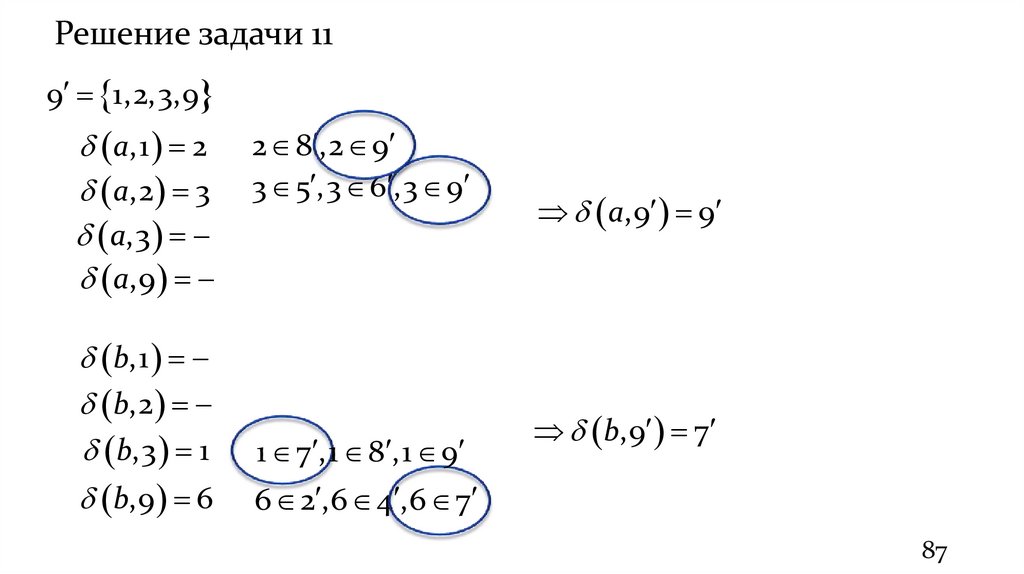
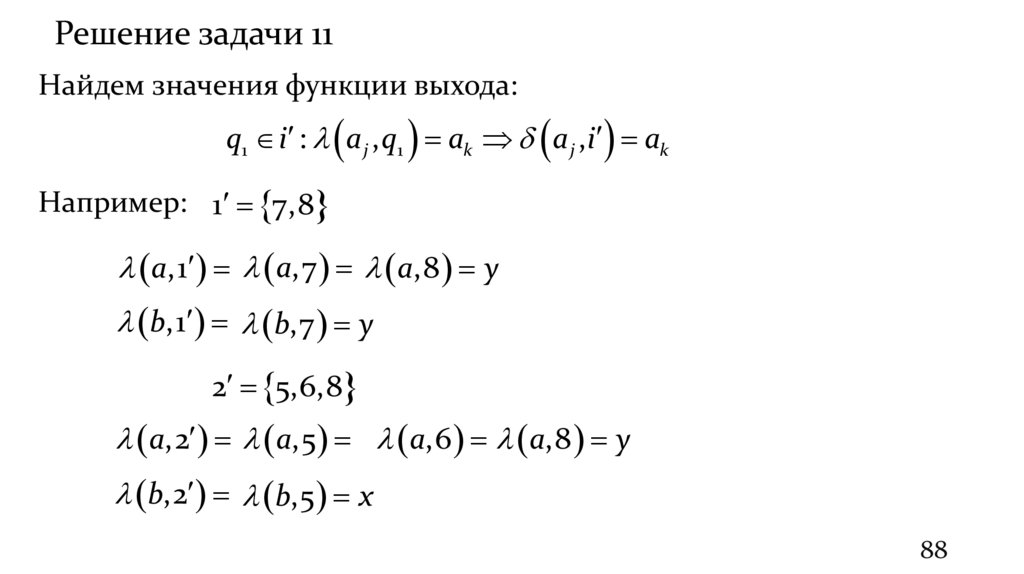
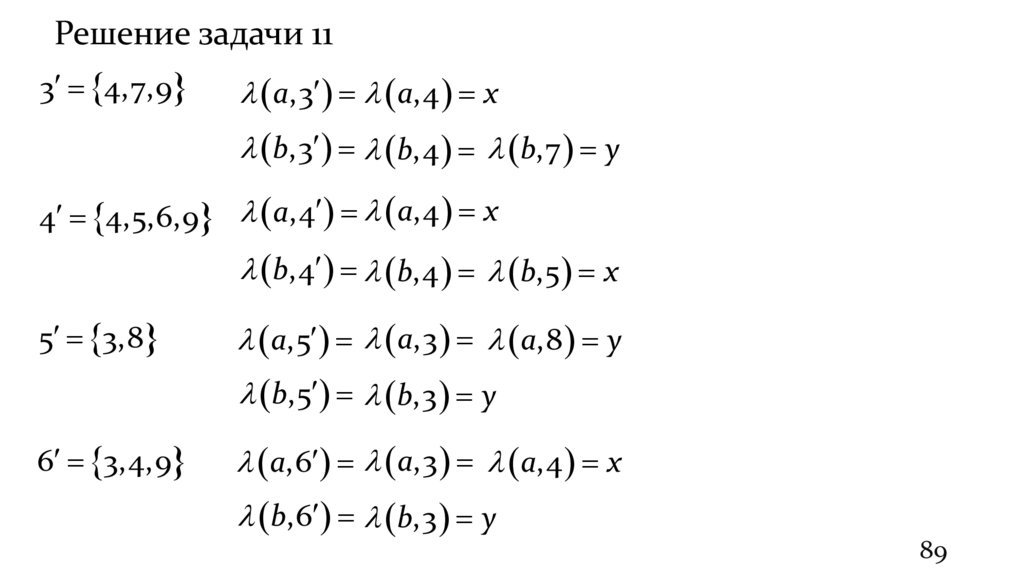
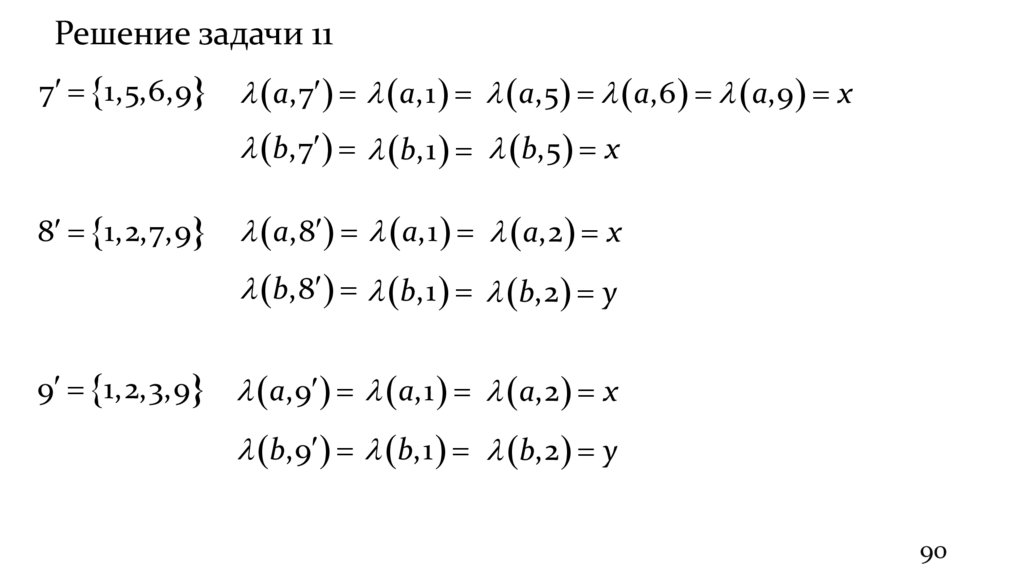













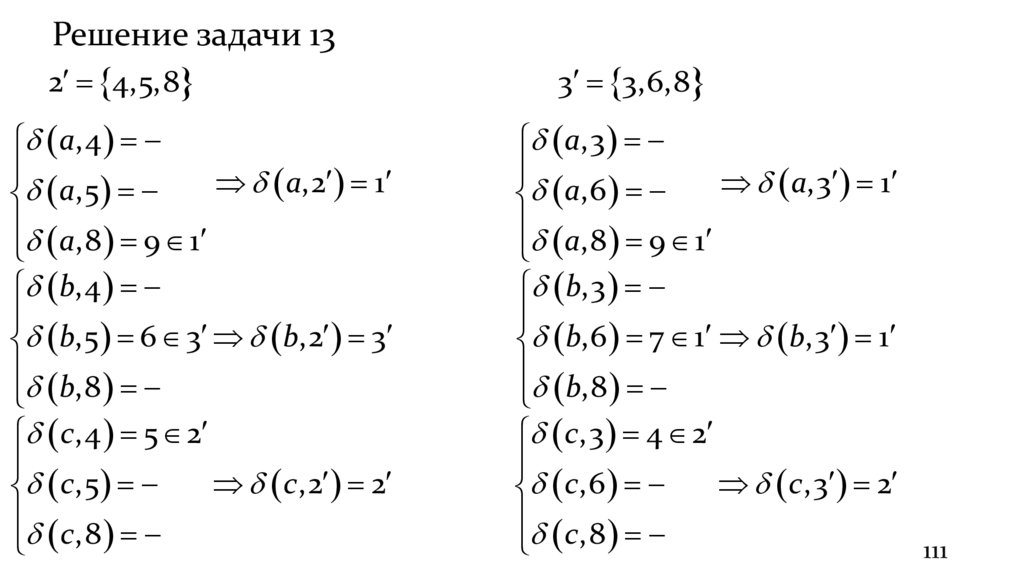
























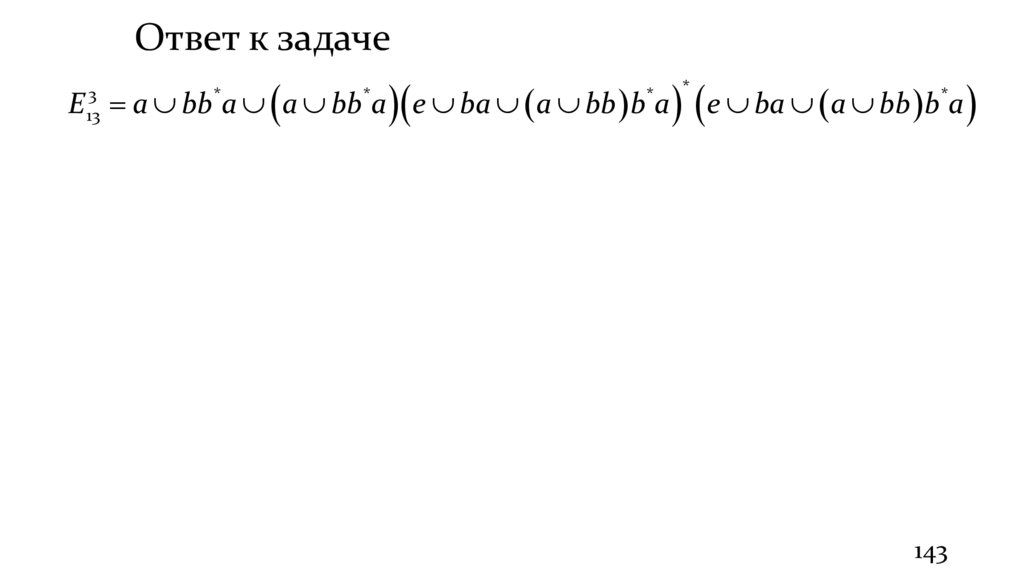
 informatics
informatics








