Создание программы для поиска парных простых чисел, превосходящих ранее найденные

1.

Государственное бюджетное общеобразовательное учреждение города
Москвы «Школа № 1155»
СОЗДАНИЕ ПРОГРАММЫ ДЛЯ ПОИСКА ПАРНЫХ ПРОСТЫХ ЧИСЕЛ,
ПРЕВОСХОДЯЩИХ РАНЕЕ НАЙДЕННЫЕ
Участник:
ученик 10 «И» класса ГБОУ Школа
№ 1155 Васильев Олег Владимирович
Руководитель:
педагог ГБОУ Школа № 1155
Юсупова Кристина Олеговна
Москва, 2025

2.

Цель работы
Целью моего проекта являются создание алгоритма по поиску простых чиселблизнецов и его программная реализация для нахождения нового наибольшего числаблизнеца.
2

3.

Программные средства
Среда программирования Visual Studio Code
Язык программирования C++
Библиотеки GMP и OpenMP
3

4.

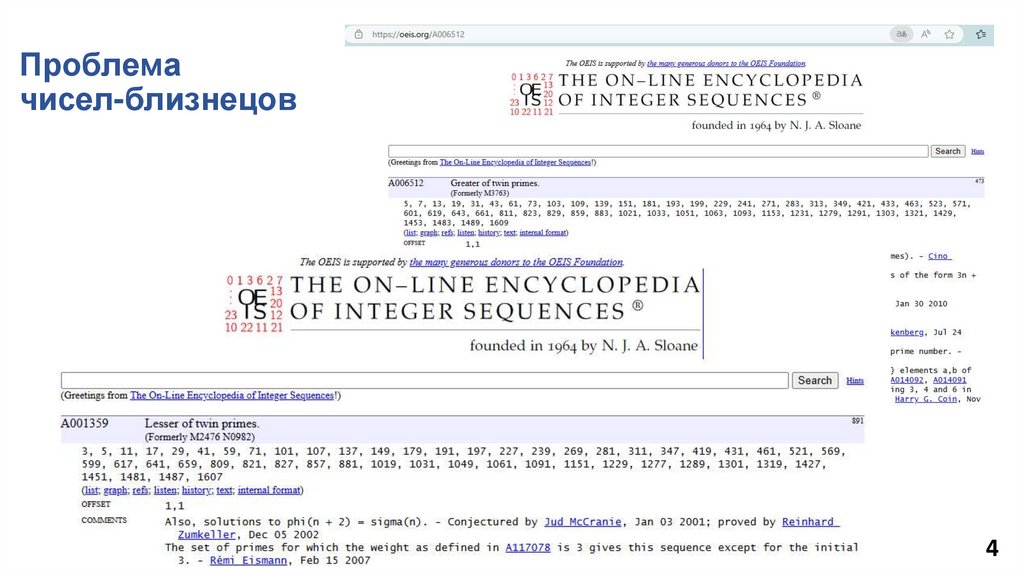
Проблема
чисел-близнецов
4

5.

Начало алгоритма
Изначально генерируются числа вида 6k ± 1, начиная от наибольшего известного числа
близнеца – 2996863034895 * 21290000 ± 1
5

6.

Проверка на простоту
После этого полученные числа проходят проверяются на простоту,
при помощи теста
алгоритма состоящего из двух частей:
1. тест на деление на простые числа до 10000
2. тест Миллера – Рабина (вероятностный тест на простоту)
Встроенная функция библиотеки GMP оказалась быстрее чем написанный вручную алгоритм,
так что была использована именно она.
6

7.

Тест Миллера-Рабина
Малая теорема Ферма:
Если n – простое число, и ‘a’ целое число не делящееся на n, то an - 1 ≡ 1 (mod n).
1. Пусть n – число которое надо проверить на простоту. Представляем число n - 1 в виде d * 2s,
где d – нечетное целое число и s – максимально возможное целое число.
2. Берём случайное число ‘a’ из отрезка [2; n – 2].
3. Считаем x = ad mod n. Если x равен 1 или n – 1, то n вероятно простое, выбираем новое ‘a’.
4. Иначе на s – 1 итерациях цикла, вычисляем x = x2 mod n
• Если x = 1, число составное.
• Если x = n – 1, число вероятно простое, выбираем новое ‘a’.
5. Если на всех s – 1 итерациях x не было равно n – 1, то число n составное.
6. Число простое, если за все итерации не было доказано иное.
7

8.

Параллельные вычисления
Благодаря параллельным вычислениям
была достигнута высокая
производительность программы, например
был использован цикл в каждом потоке
которого числа проверялись на простоту.
8

9.

Формат вывода
Для удобства записи числа будут
выводиться в формате n * 2s ± 1, в
случае если они простые и
небольшая пометка с количеством
проверенных чисел, если числа
оказались составными.
Вывод чисел
простых чисел
Вывод составных
чисел
9

10.

Удаленный сервер
Для лучшей производительности
программа была запущена на
удаленном сервере, основной
деталью которого был процессор
AMD Ryzen 9 5900X, который имеет
12 ядер и 24 потока с частотой 3.7
ГГц. Для доступа к серверу
Сервер был приобретён здесь:
https://hostkey.ru/dedicated-servers/ultra-fast/#
используется IPMI интерфейс.
10

11.

Вывод и результаты
В рамках текущего проекта создана программа, с помощью которой мы стремимся к
обнаружению новых рекордных пар чисел-близнецов, что, как ожидается, внесет
существенный вклад в теорию чисел.
Для поставленной цели было изучено много материала об истории данного
математического соревнования по поиску чисел; был освоен весь необходимый материал
по реализованным в проекте тестам на определение принадлежности чисел к простым
числам, улучшены навыки программирования на выбранном языке (знакомство с новыми
библиотеками, возможностями организации структуры программы для эффективной
работы). Данное исследование подтверждает, что применение модифицированных
приемов и программных подходов в решении поставленной проблемы может привести к
новым значимым открытиям как в области математики, так и в программировании.
11

12.

Список литературы
1.
К.
Ю.
Поляков.
Программирование.
Python.
C++
:
учебное
пособие
для
пособие
для
пособие
для
пособие
для
общеобразовательных организаций : в 4 ч. : издание «Просвещение» / Ч. 1
2.
К.
Ю.
Поляков.
Программирование.
Python.
C++
:
учебное
общеобразовательных организаций : в 4 ч. : издание «Просвещение» / Ч. 2
3.
К.
Ю.
Поляков.
Программирование.
Python.
C++
:
учебное
общеобразовательных организаций : в 4 ч. : издание «Просвещение» / Ч. 3
4.
К.
Ю.
Поляков.
Программирование.
Python.
C++
:
учебное
общеобразовательных организаций : в 4 ч. : издание «Просвещение» / Ч. 4
5.
Тест
простоты
Миллера-Рабина
[Электронный
ресурс]
URL:
https://foxford.ru/wiki/informatika/test-prostoty-millera-rabina (дата обращения: 13 ноября 2024)
6.
Онлайн-энциклопедия целочисленных последовательностей (OEIS) [Электронный
ресурс] URL: oeis.org (дата обращения: 6.09.24)
11

13.

Спасибо за внимание!