Извлечение квадратных корней без калькулятора

1.

Извлечение квадратных корней без
калькулятора

2.

Формула Древнего Вавилона
Последовательность нахождения:
• Представить число х в виде суммы: х=а2 + b, где а2 ближайший к
числу х точный квадрат натурального числа а.
• Использовать формулу:
Пример: вычислить 28.
Преимущества - дает хорошее приближение к точному значению
корня.
Недостатки - знания полных квадратов больших чисел и формулы

3.

Канадский метод
Формула:
где X - число, из которого необходимо извлечь квадратный корень,
S - число ближайшего точного квадрата
Пример:
Преимущества - метод не сложный и удобный.
Недостатки - его точность – не более двух – трёх знаков после
запятой.

4.

.
Метод Ньютона
Пусть а1 — первое приближение числа (в качестве а1 можно
брать значения квадратного корня из натурального числа —
точного квадрата, не превосходящего х). Следующее, более точное
приближение а2 числа
найдется по формуле
(n+1)-е приближение найдется по формуле
Пример:
нахождение приближенного значения числа 28 методом Ньютона
дает следующие результаты: а1 =5; а2 = 5,3; а3 =5,2915.
Преимущества - позволяет извлекать квадратный корень из
большого числа с любой точностью.
Недостатки - громоздкость вычислений.

5.

.
.
Метод оценки
Последовательность решения:
• Выяснить диапазон, в котором лежит исходный корень (100;
400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000).
• По последней цифре определить на какую цифру заканчивается
искомое число.
• Возвести в квадрат предполагаемые числа и определить из них
искомое число.
Пример: вычислить
3364
Преимущества - овладеть этим способом может каждый.
Недостатки - требует многократного вычисления произведения
столбиком не всегда правильно угаданных чисел.

6.

.
.
Метод разложения на простые множители
Суть метода: для извлечения квадратного корня можно разложить число на
простые множители и извлечь квадратный корень из произведения.
Пример: вычислить
.
Преимущества - многие применяют его успешно и считают единственным.
Недостатки - нужно знать простые числа и признаки делимости;
трудоёмкая задача; занимает много времени.

7.

.
.
Метод вычетов нечетного числа
Суть метода: чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по
порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество
выполненных действий.
Пример: найдем √16 так:
1. 16 - 1 = 15
2. 15 - 3 = 12
3. 12 - 5 = 7
4. 7 - 7 =0
Выполнено 4 действия, значит √16 = 4
Преимущества - прост в применении.
Недостатки - если извлекаемый корень не является целым числом, то можно узнать только его целую
часть.

8.

.
.
Алгоритм:
Извлечение квадратного корня уголком
1. Разбиваем число (5963364) на пары справа налево
(5`96`33`64)
2. Извлекаем квадратный корень из первой слева
группы
7. Ищем вторую цифру числа b: удвоенная
первая цифра, найденная нами, становится
цифрой десятков числа, при умножении
которого на число единиц, необходимо
получить число меньшее 196 (это цифра 4,
44*4=176). 4 - вторая цифра числа b.
( - число 2). Так мы получаем первую цифру числа b.
8. Находим разность (196-176=20).
3. Находим квадрат первой цифры (22=4).
9. Сносим следующую группу (получаем число
2033).
4. Находим разность первой группы и квадрата
первой цифры (5-4=1).
5.Сносим следующие две цифры (получили число
196).
6. Удваиваем первую, найденную нами цифру,
записываем слева за чертой (2*2=4).
10. Удваиваем число 24, получаем 48.
11. 48 десятков в числе, при умножении
которого на число единиц, мы должны получить
число меньшее 2033 (484*4=1936). Найденная
нами цифра единиц (4) и есть третья цифра
числа b.
Далее процесс повторяется.

9.

.
.
Извлечение квадратного корня уголком
Пример:
Преимущества - очень точный (можно
вычислить корень из любого числа с любой
точностью);применим к любым числам.
Недостатки - трудоемкий; требует
хороших вычислительных навыков

10.

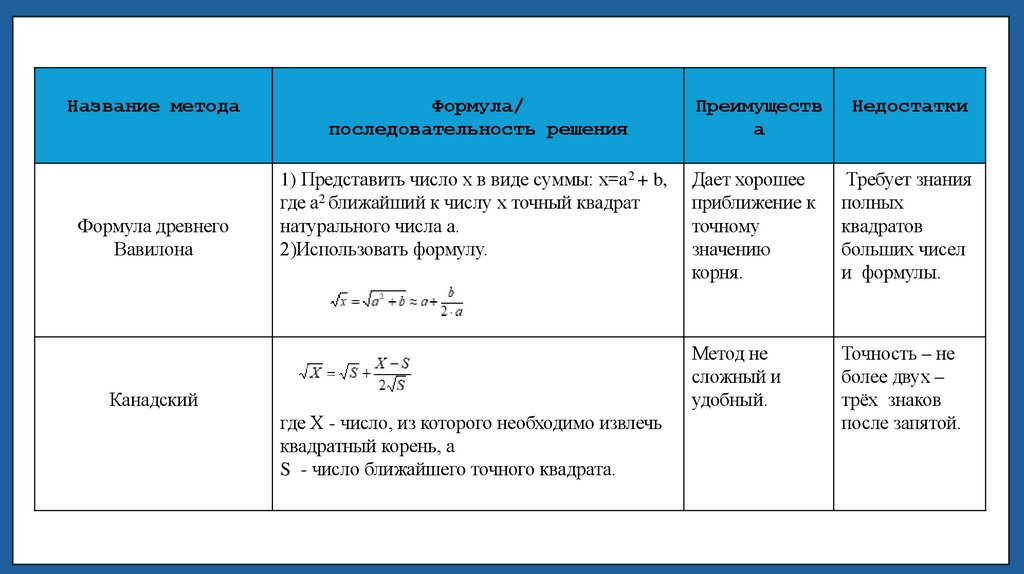
Название метода
Формула древнего
Вавилона
Формула/
последовательность решения
Преимуществ
а
Недостатки
1) Представить число х в виде суммы: х=а2 + b,
где а2 ближайший к числу х точный квадрат
натурального числа а.
2)Использовать формулу.
Дает хорошее
приближение к
точному
значению
корня.
Требует знания
полных
квадратов
больших чисел
и формулы.
Метод не
сложный и
удобный.
Точность – не
более двух –
трёх знаков
после запятой.
Канадский
где X - число, из которого необходимо извлечь
квадратный корень, а
S - число ближайшего точного квадрата.

11.

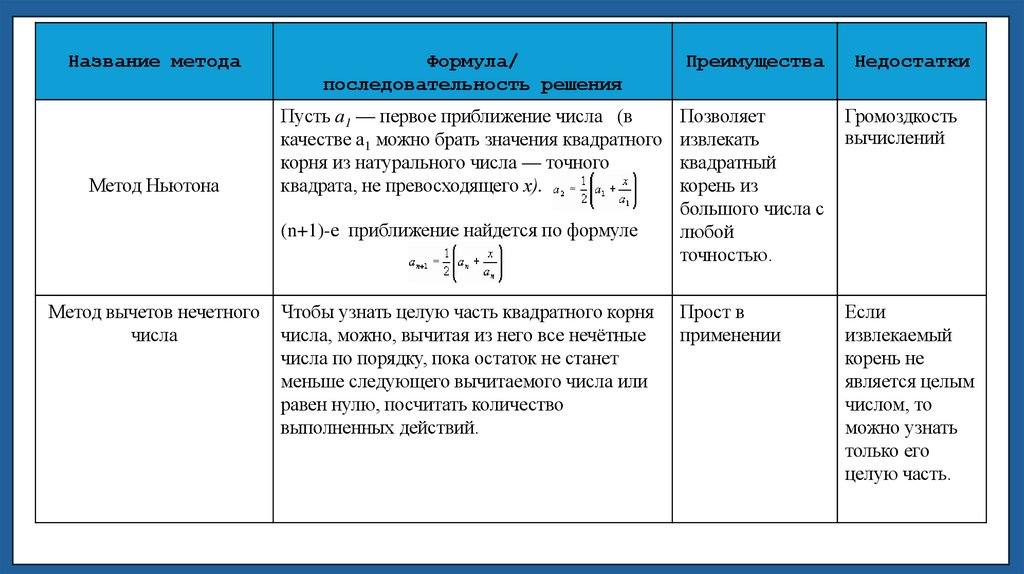
Название метода
Метод Ньютона
Формула/
последовательность решения
Преимущества
Недостатки
Пусть а1 — первое приближение числа (в
качестве а1 можно брать значения квадратного
корня из натурального числа — точного
квадрата, не превосходящего х).
Позволяет
извлекать
квадратный
корень из
большого числа с
любой
точностью.
Громоздкость
вычислений
Прост в
применении
Если
извлекаемый
корень не
является целым
числом, то
можно узнать
только его
целую часть.
(n+1)-е приближение найдется по формуле
Метод вычетов нечетного
числа
Чтобы узнать целую часть квадратного корня
числа, можно, вычитая из него все нечётные
числа по порядку, пока остаток не станет
меньше следующего вычитаемого числа или
равен нулю, посчитать количество
выполненных действий.

12.

Название метода
Метод оценки
Метод разложения на
простые множители
Формула/
последовательность решения
Преимущества
Недостатки
1)Выяснить диапазон, в котором лежит исходный
корень (100; 400; 900; 1600; 2500; 3600; 4900; 6400;
8100; 10 000).
2)По последней цифре определить на какую
цифру заканчивается искомое число.
3)Возвести в квадрат предполагаемые числа и
определить из них искомое число.
Овладеть этим
способом может
каждый.
Требует
Для извлечения квадратного корня можно
разложить число на простые множители и
извлечь квадратный корень из произведения
Многие
применяют его
успешно и
считают
единственным.
Нужно знать
простые числа и
признаки
делимости;
многократного
вычисления
произведения
столбиком не
всегда
правильно
угаданных
чисел.
трудоёмкая
задача; занимает
много времени.

13.

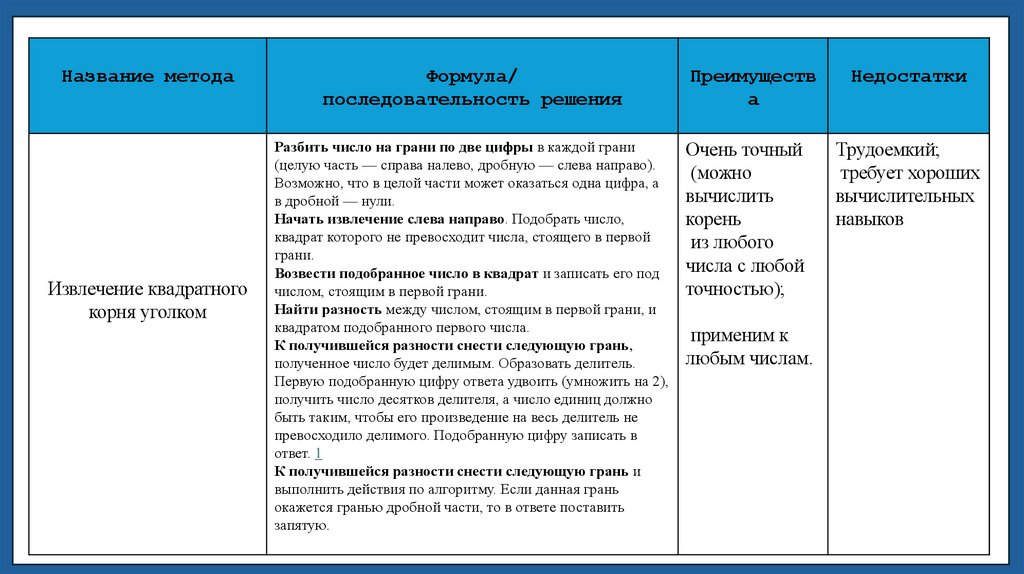
Название метода
Извлечение квадратного
корня уголком
Формула/
последовательность решения
Преимуществ
а
Недостатки
Разбить число на грани по две цифры в каждой грани
(целую часть — справа налево, дробную — слева направо).
Возможно, что в целой части может оказаться одна цифра, а
в дробной — нули.
Начать извлечение слева направо. Подобрать число,
квадрат которого не превосходит числа, стоящего в первой
грани.
Возвести подобранное число в квадрат и записать его под
числом, стоящим в первой грани.
Найти разность между числом, стоящим в первой грани, и
квадратом подобранного первого числа.
К получившейся разности снести следующую грань,
полученное число будет делимым. Образовать делитель.
Первую подобранную цифру ответа удвоить (умножить на 2),
получить число десятков делителя, а число единиц должно
быть таким, чтобы его произведение на весь делитель не
превосходило делимого. Подобранную цифру записать в
ответ. 1
К получившейся разности снести следующую грань и
выполнить действия по алгоритму. Если данная грань
окажется гранью дробной части, то в ответе поставить
запятую.
Очень точный
(можно
вычислить
корень
из любого
числа с любой
точностью);
Трудоемкий;
требует хороших
вычислительных
навыков
применим к
любым числам.