Эффективность алгоритмов. Основные понятия

1. Эффективность алгоритмов. Основные понятия

Не все, что можно подсчитать, принимают в расчет,
и не все, что принимают в расчет, можно подсчитать.
— Альберт Эйнштейн (Albert Einstein) (1824-1907)

2.

Анализ алгоритмов
Процесс исследования
эффективности алгоритмов
Время
Объем памяти

3.

Определение временной эффективности
алгоритмов
1.
Оценка размера входных данных
a. эффективность алгоритма – функция от
некоторого параметра n, связанного с размером
входных данных
b. обработка списков – размер списка
c. работа с многочленами – степень, число
коэффициентов
d. Нахождение чисел, удовлетворяющих
некоторым условиям – количество битов в их
двоичном представлении: b=[log2n]+1

4.

Определение временной эффективности
алгоритмов
2.
Единицы измерения времени выполнения
алгоритма
a. показатель для анализа временной
эффективности алгоритмов оценивается по
количеству основных операций, которые должен
выполнить алгоритм при обработке входных
данных размера n

5.

СОР — время выполнения основной операции
алгоритма на конкретном компьютере
С (n) — количество раз, которые эта операция
должна быть выполнена при работе алгоритма
T(n)≈ СОР С (n)

6.

Пусть С(n) = n(n — 1)/2
Вопрос: Насколько дольше будет
выполняться программа, если удвоить
размер входных данных?
Ответ: приблизительно в 4 раза медленне
Решение:

7.

Определение временной эффективности
алгоритмов
3.
Порядок роста
a. для анализа эффективности алгоритма
вычисляют не реальное значение количества
основных операций, а оценивают порядок роста
(order of growth) количества основных операций
в зависимости от размера входных данных.

8. Приближенные значения важных для анализа алгоритмов функций

2100 операций, производительность 1012 оп/сек - 4 • 1010 лет
100! операций – больше времени жизни планеты Земля (4.5 миллиарда лет)

9. Эффективность алгоритма в разных случаях

Пример: задача последовательного поиска
В списке нет искомого элемента, или он последний – НАИХУДШИЙ случай
Cworst (n) = n
Первый элемент равен искомому – НАИЛУЧШИЙ случай
Cbest (n) = 1
Искомый элемент в произвольном месте списка – СРЕДНИЙ случай
если p-вероятность успешного поиска, то

10. Классы эффективности Ο,Ω и Θ

пусть t(n) и g(n) – любые неотрицательные функции,
определенными на множестве натуральных чисел
t (n) - время выполнения алгоритма
g(n) - некоторая простая функция, с которой будет
проводиться сравнение количества операций

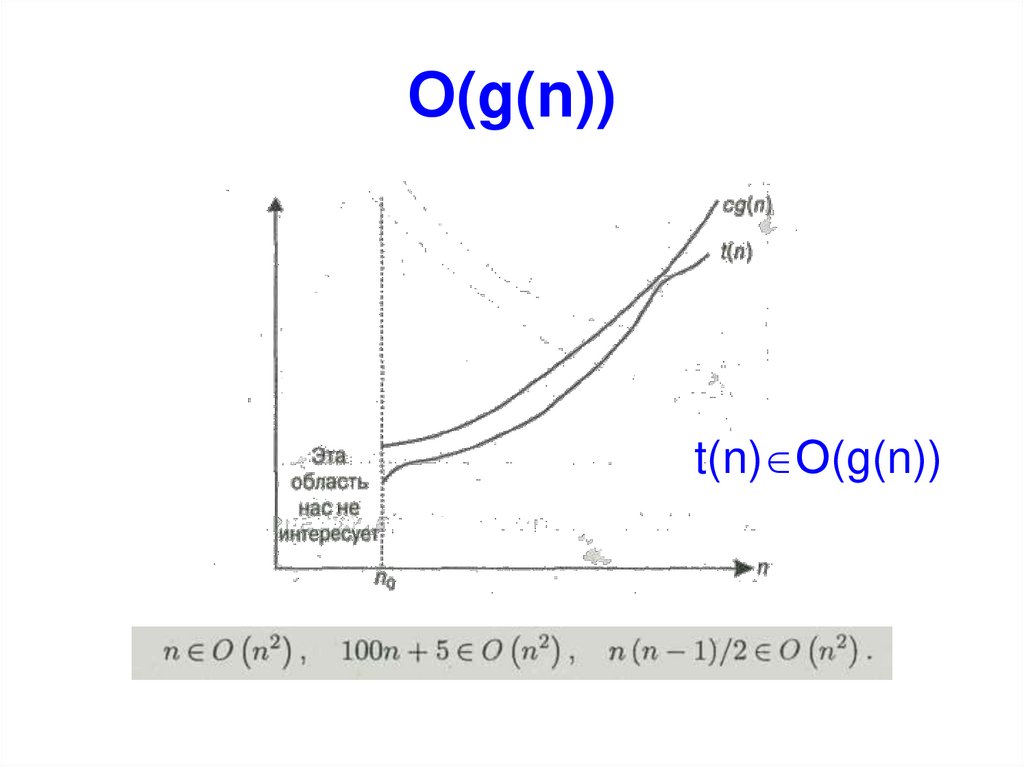
11. Ο(g(n))

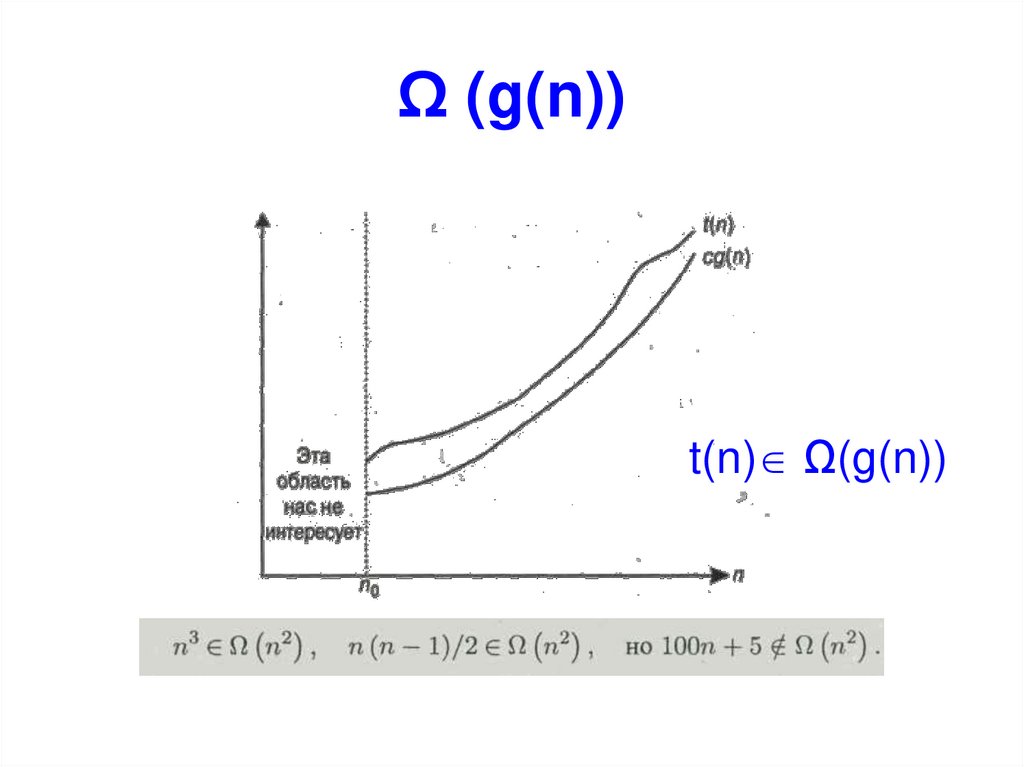
t(n) Ο(g(n))

12. Ω (g(n))

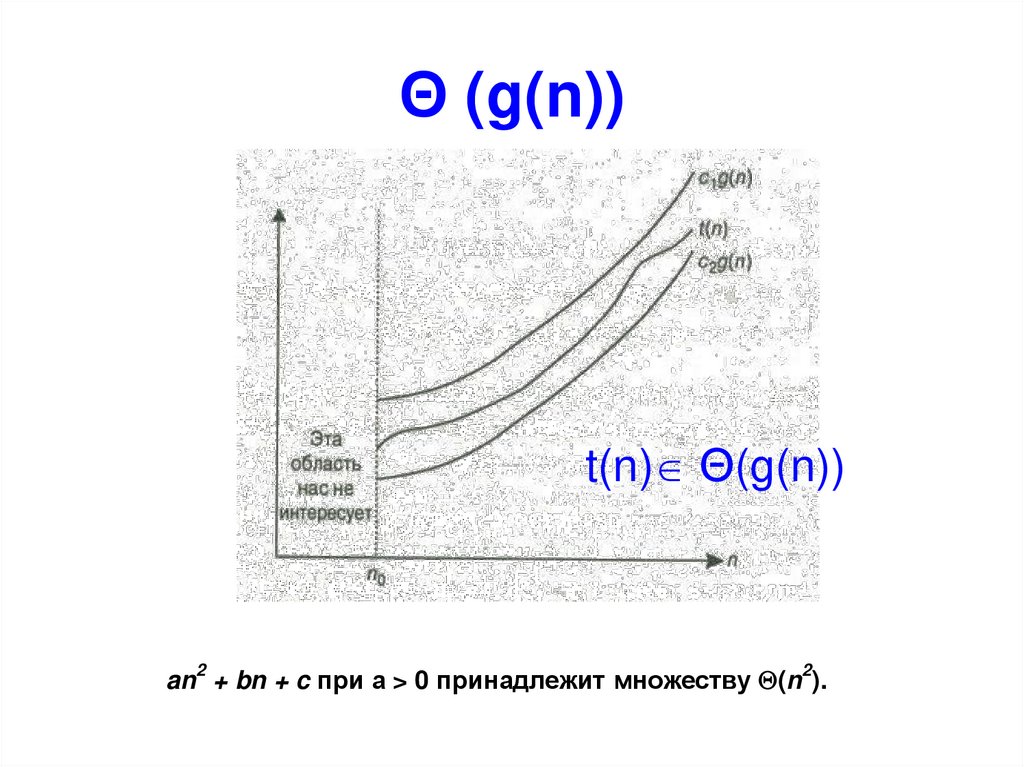
t(n) Ω(g(n))

13. Θ (g(n))

t(n) Θ(g(n))
an + bn + c при а > 0 принадлежит множеству (n ).
2
2

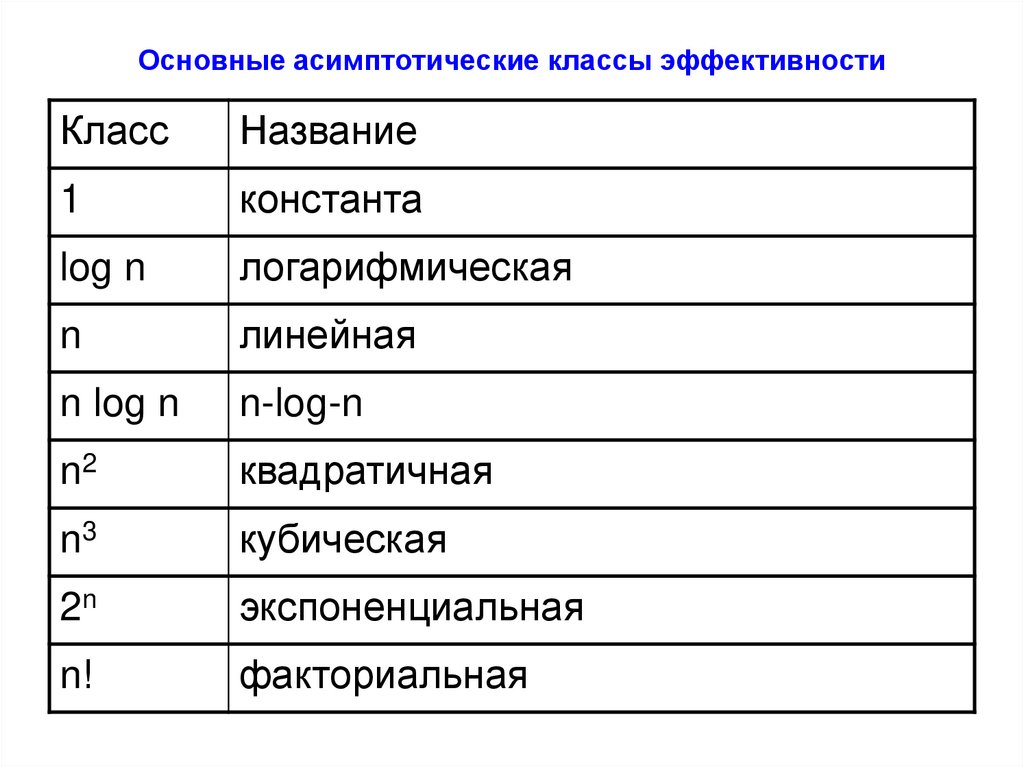
14. Основные асимптотические классы эффективности

Класс
Название
1
константа
log n
логарифмическая
n
линейная
n log n
n-log-n
n2
квадратичная
n3
кубическая
2n
экспоненциальная
n!
факториальная

15.

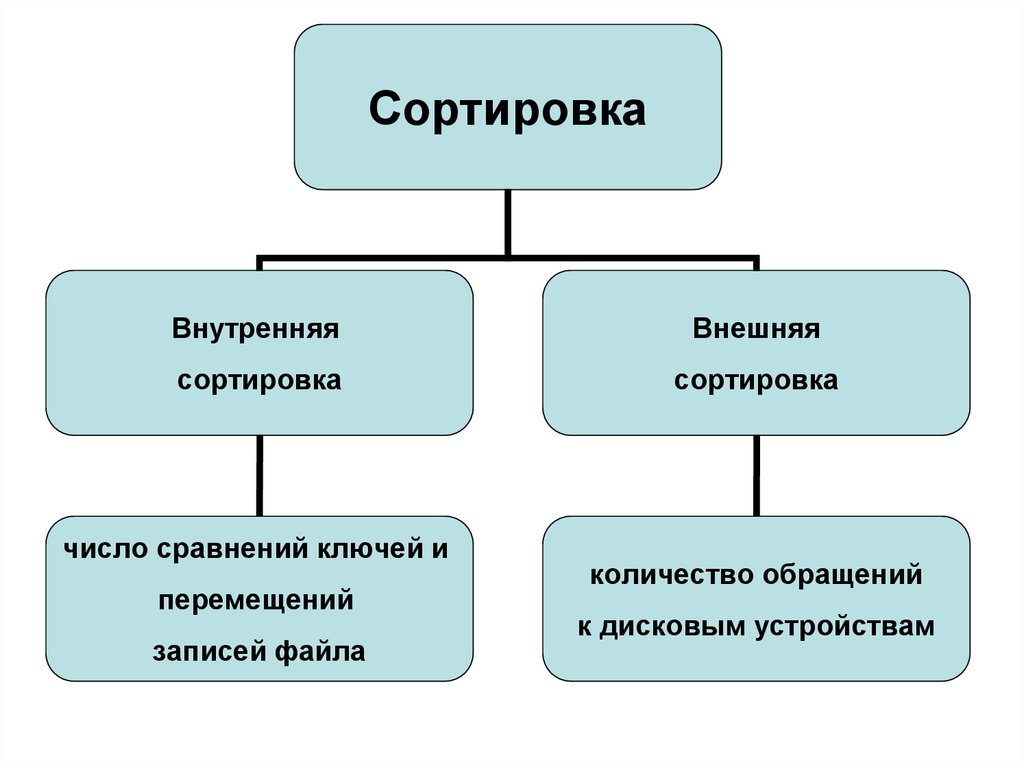
16. Внутренние и внешние сортировки

λ(1), λ(2), …, λ(n)
λ(i) ключ Kλ(i) (i=1,2,…,n)
µ(1), µ(2), …, µ(n),
Kµ(1) ≤ Kµ(2) ≤ … ≤ Kµ(n)
(1)

17.

Сортировка
Внутренняя
Внешняя
сортировка
сортировка
число сравнений ключей и
перемещений
записей файла
количество обращений
к дисковым устройствам

18. Внутренние сортировки. Сортировка простым выбором (selection sort)

для i от 0 до предпоследнего (n-2)
{
min=i;
для j от i+1 до последнего (n-1)
{
если t[j] < t[min] то
min=j;
t[i]=t[i]+t[min];
t[min]=t[i]-t[min];
t[i]=t[i]-t[min];
}
}
обмен t[i] и t[min] без
дополнительной
переменной
2и3
2=2+3=5, 3=5-3=2, 5=5-2=3

19. Сортировка простым выбором

3 2
4
1
13
5
внешний цикл первый проход:
i=0
j от 1 до 5
j=1: t[1](2)<t[0](3) да, мен
2
3
4
j=2: t[2](4)<t[0](2) нет, не мен 2
3
4
j=3: t[3](1)<t[0](2) да, мен
1
3
4
j=4: t[4](13)<t[0](1) нет, не ме 1
3
4
j=5: t[5](5)<t[0](1) нет, не мен 1
3
4
в результате первого прохода внешнего цикла –
на месте наименьшее число.
внешний цикл второй проход:
i=1
j от 2 до 5
j=2: t[2](4)<t[1](3) нет, не мен 1
j=3: t[3](2)<t[1](3) да, мен
1
j=4: t[4](13)<t[1](2) нет, не ме 1
j=5: t[5](5)<t[1](2) нет, не мен 1
3
2
2
2
4
4
4
4
1
1
2
2
2
13
13
13
13
13
5
5
5
5
5
2
3
3
3
13
13
13
13
5
5
5
5

20. Код на С. Функция сортировки простым выбором одномерного целочисленного массива a размерностью n

void sort_VIBOR(int *a,int n)
{
int i,j,temp,min;
for (i=0;i<n-1;i++)
{
min=i;
for (j=i+1;j<n;j++)
if (a[j] < a[min])
{
min=j;
temp=a[i];
a[i] =a[min];
a[min]=temp;
}
}
}

21. Сортировка простым выбором

Анализ:
размер входных данных – количество элементов в списке
базовая операция – сравнение
Общее количество сравнений – C (n)
n 2 n 1
n 2
i 0 j i 1
i 0
1 (n 1 i)
Алгоритм сортировки выбором принадлежит
классу Θ(n2)
(n 1)n
2

22.

http://www.sorting-algorithms.com/selection-sort

23. Сортировка пузырьком (простыми обменами)

Начальное сост. массива
8 23 5 65 44 33 1 6
Шаг 1
8 23 5 65 44 33 1 6
8 23 5 65 44 1 33 6
8 23 5 65 1 44 33 6
8 23 5 1 65 44 33 6
8 23 1 5 65 44 33 6
8 1 23 5 65 44 33 6
1 8 23 5 65 44 33 6
Шаг 2
1 8 23 5 65 44 6 33
1 8 23 5 65 6 44 33
1 8 23 5 6 65 44 33
1 8 23 5 6 65 44 33
1 8 5 23 6 65 44 33
1 5 8 23 6 65 44 33
Шаг 3
1 5 8 23 6 65 33 44
1 5 8 23 6 33 65 44
1 5 8 23 6 33 65 44
1 5 8 6 23 33 65 44
1 5 6 8 23 33 65 44
Шаг 4
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
Шаг 5
Три прохода, перестановок нет
Шаг 6
Два прохода, перестановок нет
Шаг 7
Один проход, перестановок нет

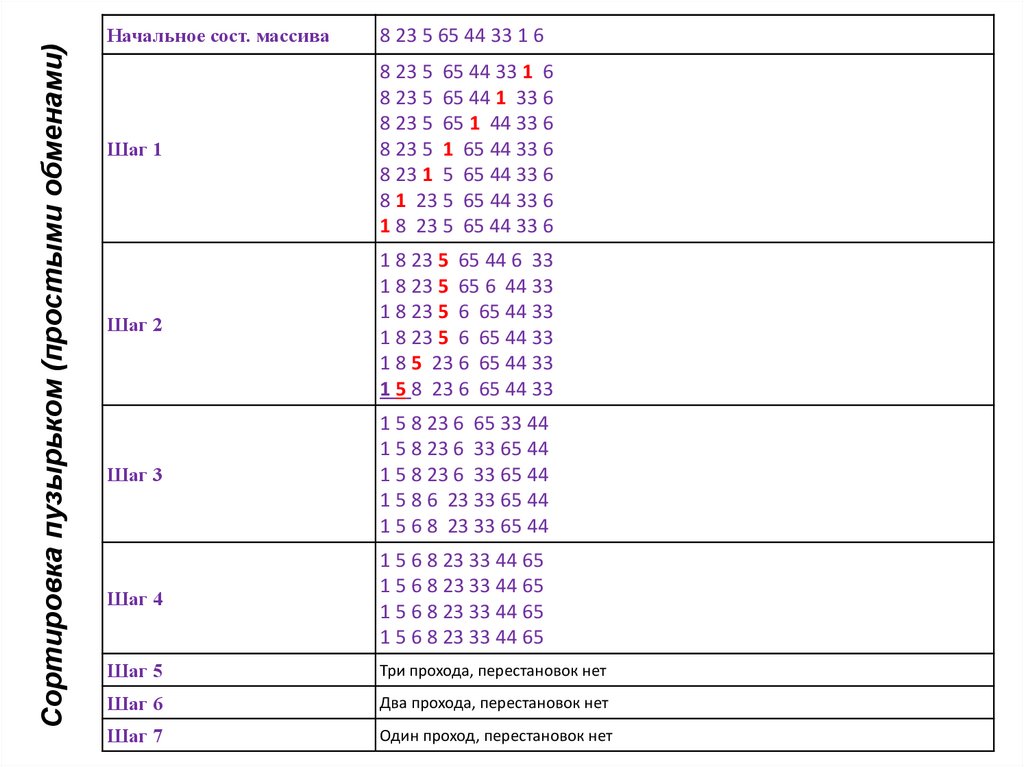
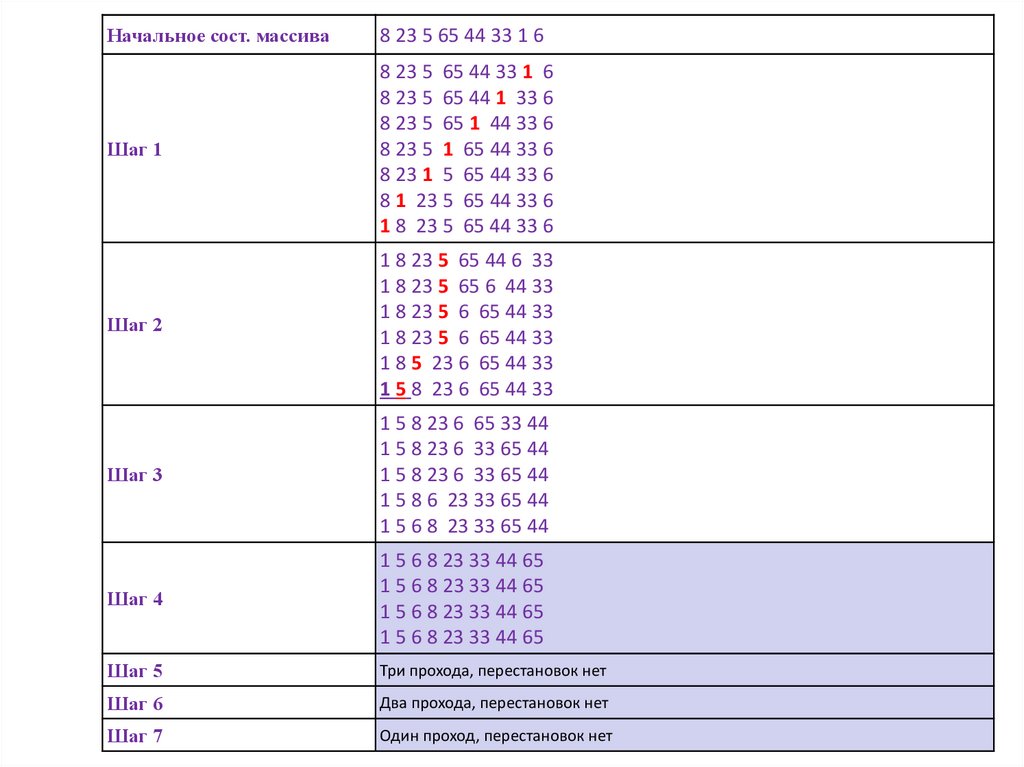
24. Сортировка пузырьком (простыми обменами)

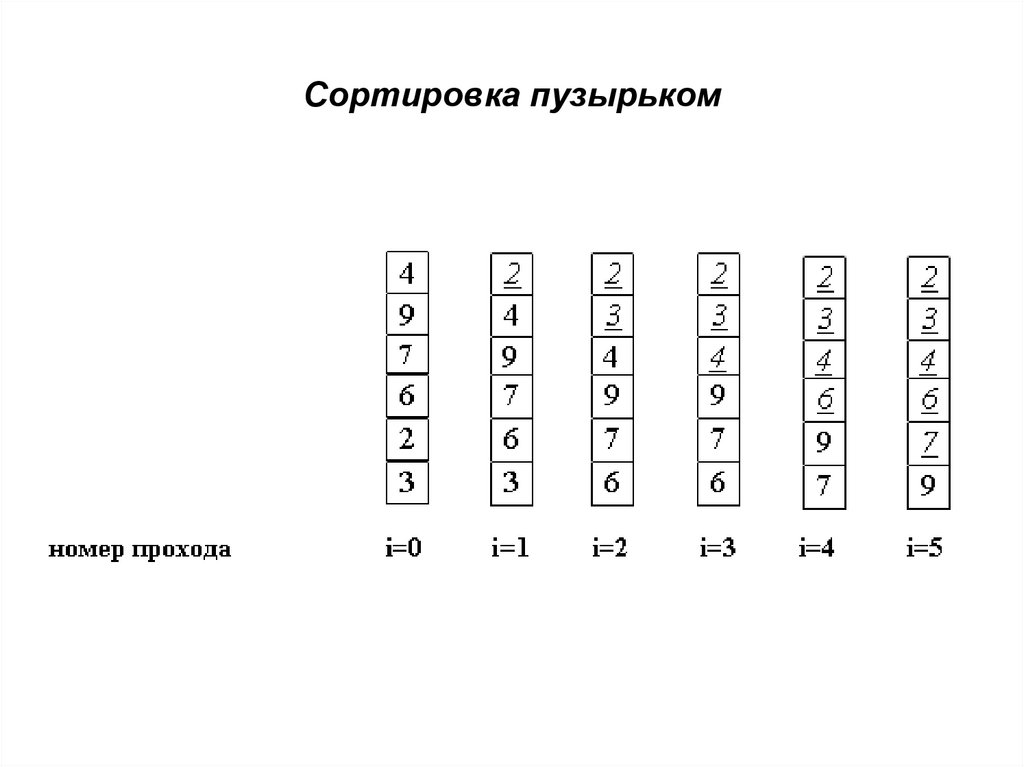
25. Сортировка пузырьком

26. Сортировка пузырьком (простыми обменами) (bubble sort)

для i от 0 до n-2 (предпоследнего)
для j от 0 до n-2-i do
если t[j+1]<t[j] то
{
h=t[j+1]; //обмен с использование дополнительной переменной
t[j+1]=t[j];
t[j]=h;
}

27. Код на С. Функция сортировки простыми обменами одномерного целочисленного массива a размерностью n

void sort(int *a,int n)
{
int i,j,temp;
for (i=0;i<=n-2;i++)
for (j=0;j<=n-2-i;j++)
if (a[j+1] < a[j])
{
temp=a[j+1];
a[j+1] =a[j];
a[j]=temp;
}
}

28. Сортировка пузырьком

Анализ:
размер входных данных – количество элементов в списке n
базовая операция – сравнение
n 2 n 2 i
n 2
i 1
i 0
Общее количество сравнений – C (n) 1 ((n 2 i) 0 1)
Алгоритм сортировки пузырьком
принадлежит классу Θ(n2)
j 0
(n 1)n
2

29.

Начальное сост. массива
8 23 5 65 44 33 1 6
Шаг 1
8 23 5 65 44 33 1 6
8 23 5 65 44 1 33 6
8 23 5 65 1 44 33 6
8 23 5 1 65 44 33 6
8 23 1 5 65 44 33 6
8 1 23 5 65 44 33 6
1 8 23 5 65 44 33 6
Шаг 2
1 8 23 5 65 44 6 33
1 8 23 5 65 6 44 33
1 8 23 5 6 65 44 33
1 8 23 5 6 65 44 33
1 8 5 23 6 65 44 33
1 5 8 23 6 65 44 33
Шаг 3
1 5 8 23 6 65 33 44
1 5 8 23 6 33 65 44
1 5 8 23 6 33 65 44
1 5 8 6 23 33 65 44
1 5 6 8 23 33 65 44
Шаг 4
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
Шаг 5
Три прохода, перестановок нет
Шаг 6
Два прохода, перестановок нет
Шаг 7
Один проход, перестановок нет

30.

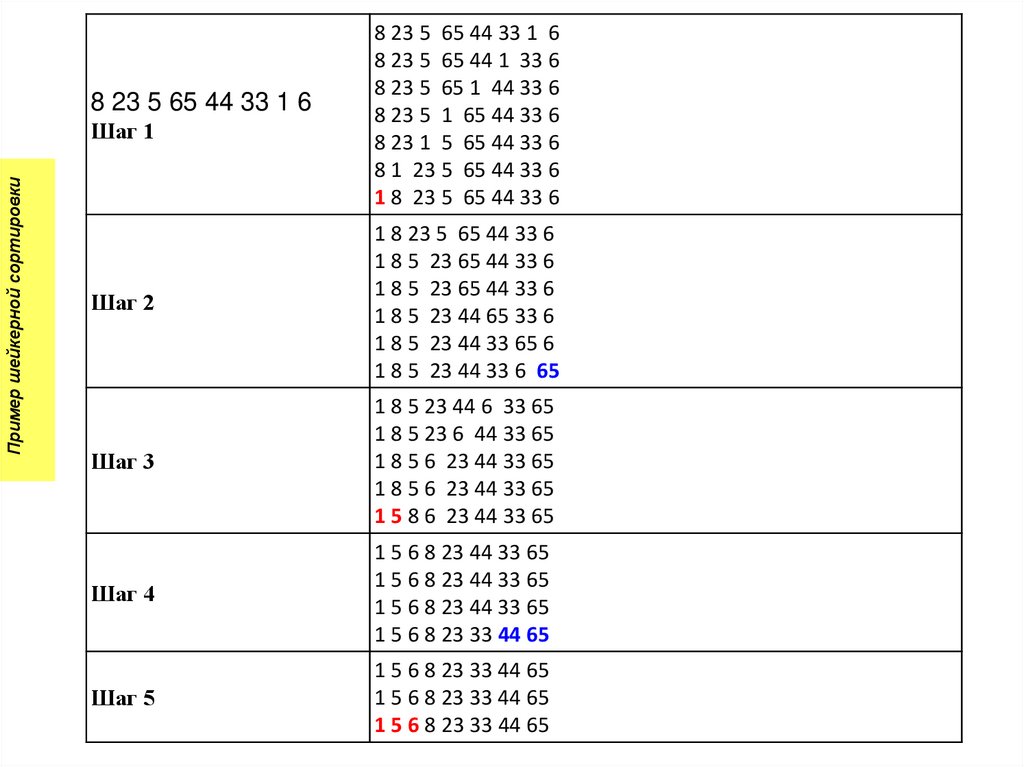
8 23 5 65 44 33 1 6
Пример шейкерной сортировки
Шаг 1
8 23 5 65 44 33 1 6
8 23 5 65 44 1 33 6
8 23 5 65 1 44 33 6
8 23 5 1 65 44 33 6
8 23 1 5 65 44 33 6
8 1 23 5 65 44 33 6
1 8 23 5 65 44 33 6
Шаг 2
1 8 23 5 65 44 33 6
1 8 5 23 65 44 33 6
1 8 5 23 65 44 33 6
1 8 5 23 44 65 33 6
1 8 5 23 44 33 65 6
1 8 5 23 44 33 6 65
Шаг 3
1 8 5 23 44 6 33 65
1 8 5 23 6 44 33 65
1 8 5 6 23 44 33 65
1 8 5 6 23 44 33 65
1 5 8 6 23 44 33 65
Шаг 4
1 5 6 8 23 44 33 65
1 5 6 8 23 44 33 65
1 5 6 8 23 44 33 65
1 5 6 8 23 33 44 65
Шаг 5
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65
1 5 6 8 23 33 44 65

31. http://www.sorting-algorithms.com/bubble-sort

32. Сортировка вставками (простыми включениями) (insertion)

InsertionSort (a,n)
a-сортируемый список элементов
n-число элементов в списке
для i=1 до n-1
new=a[i] //анализируемый элемент
j=i-1
пока (j>=0) and (a[j]>new)
a[j+1]=a[j]
{сдвигаем все элементы,
большие очередного вставляемого}
j=j-1
конец пока
a[j+1]=new
конец для

33. Код на С. Функция сортировки вставками одномерного целочисленного массива a размерностью n

void sort_VSTAV(int *a,int n)
{
int i,j,temp;
for (i=1;i<n;i++)
{
temp=a[i];
j=i-1;
while ((j>=0)&&(a[j]>temp))
{
a[j+1] =a[j];
j--;
}
a[j+1]=temp;
}
}

34. Сортировка вставками

Анализ:
размер входных данных – количество элементов в списке n
базовая операция – сравнение (a[j]>new)
Общее количество сравнений –
n 1 i 1
n 1
i 1 j 0
i 1
C (n) 1 i
Алгоритм сортировки вставками принадлежит
классу Θ(n2)
(n 1)n
2

35. http://www.sorting-algorithms.com/insertion-sort

36. Сортировка методом Шелла

s - номер шага. s от 0, останавливаться следует на значении inc[s-1], если 3*inc[s] > n
O(n7/6) в среднем
O(n4/3) в худшем случае

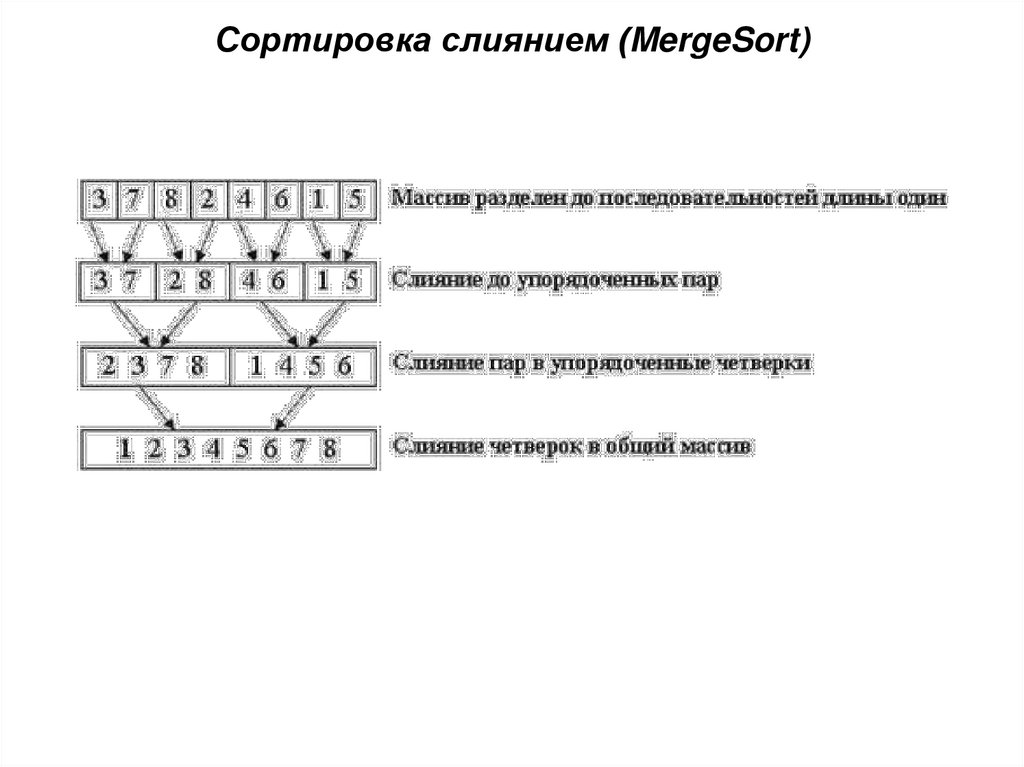
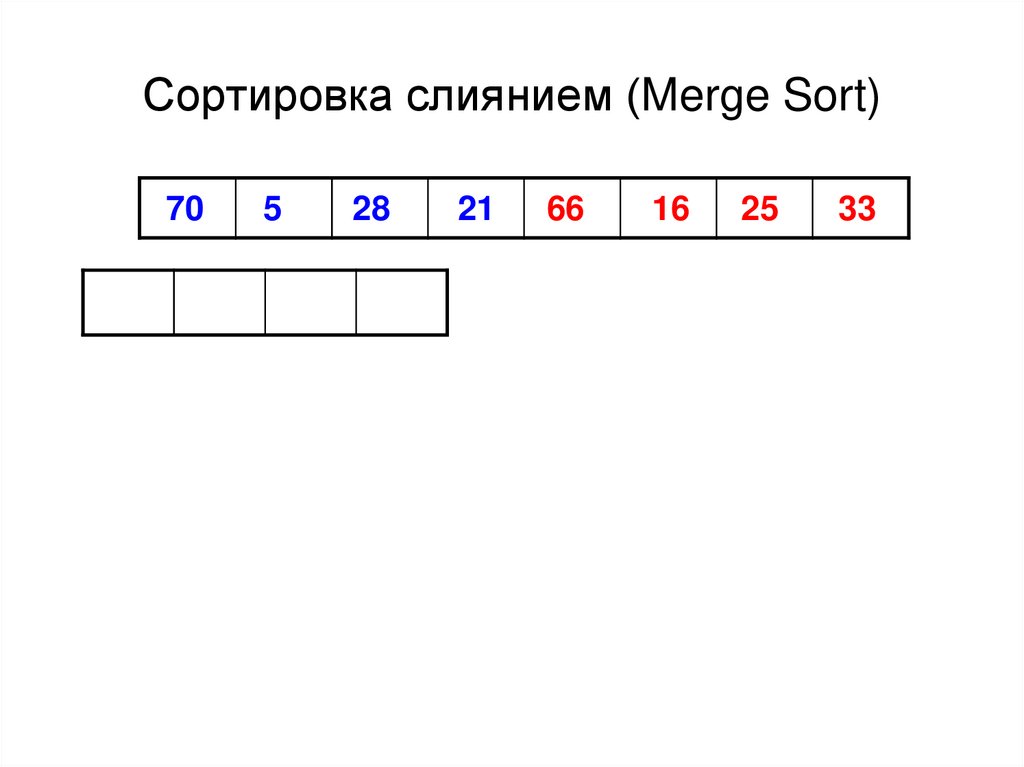
37. Сортировка слиянием (MergeSort)

38. Функция MergeSort - разбиение списка

MergeSort(list,first,last)
list – сортируемый список элементов
first – номер первого элемента в сортируемой части списка
last – номер последнего элемента в сортируемой части списка
if first<last then
middle=(first+last)/2
MergeSort(list,first,middle)
MergeSort(list,middle+1,last)
MergeList(list,first,middle,middle+1,last)
end if

39. Функция MergeSort - разбиение списка

Алгоритм сортировки слияниями принадлежит классу Θ(n·lg(n))

40. Сортировка слиянием (Merge Sort)

70
5
28
21
66
16
25
33

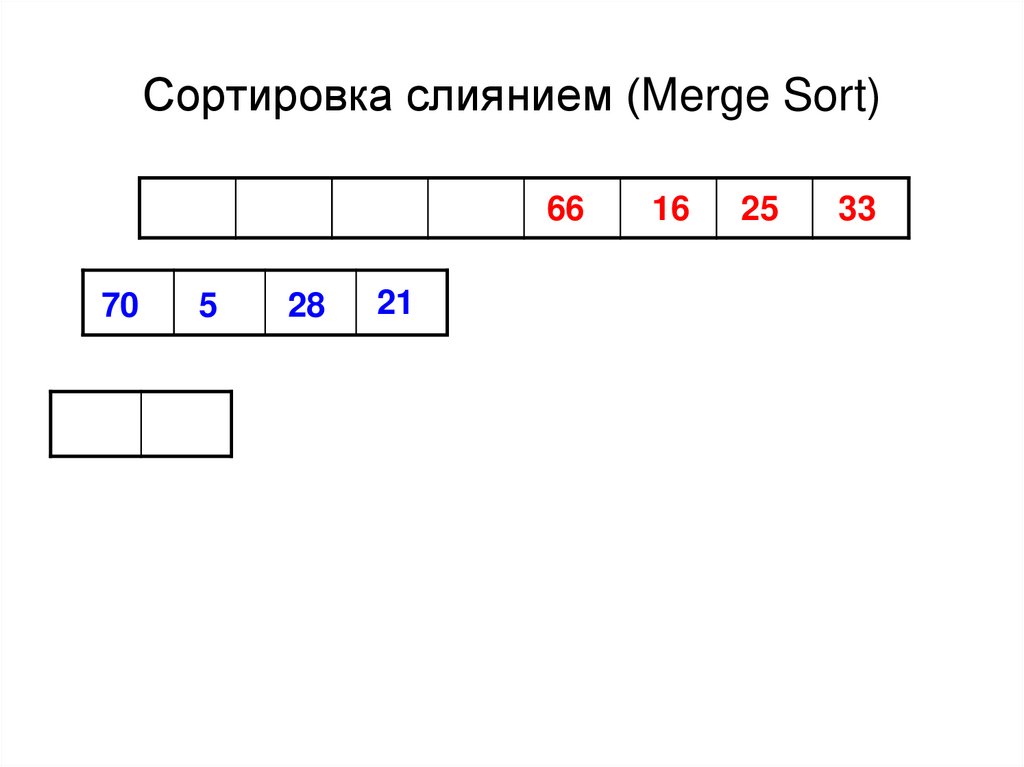
41. Сортировка слиянием (Merge Sort)

66
70
5
28
21
16
25
33

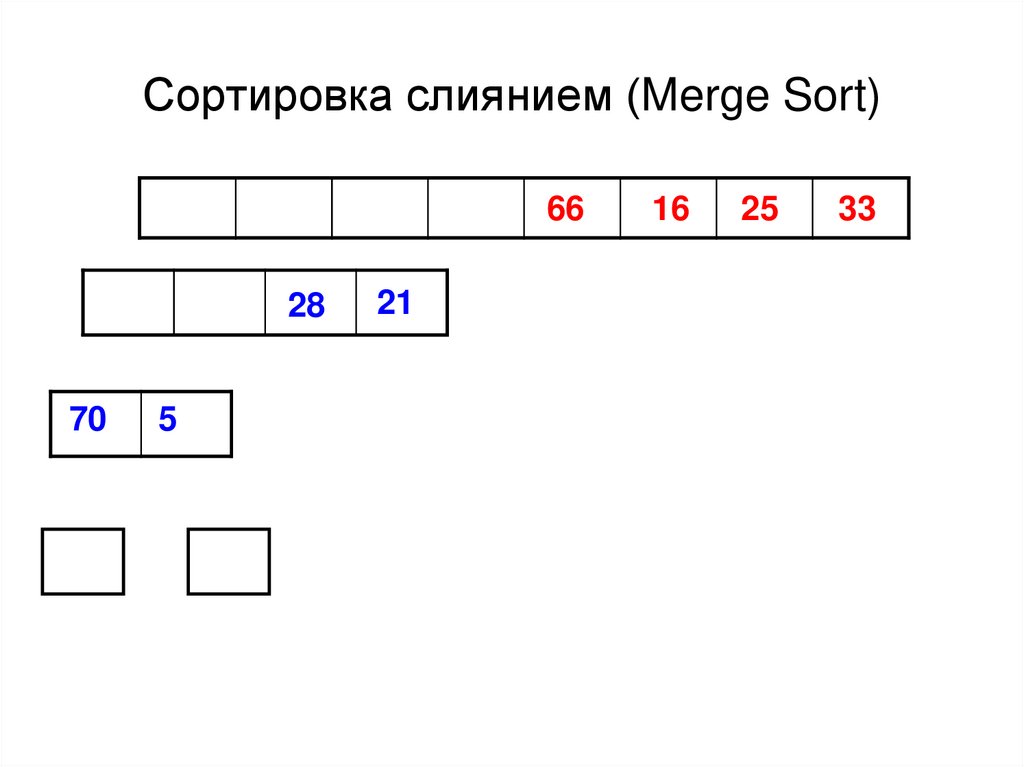
42. Сортировка слиянием (Merge Sort)

66
28
70
5
21
16
25
33

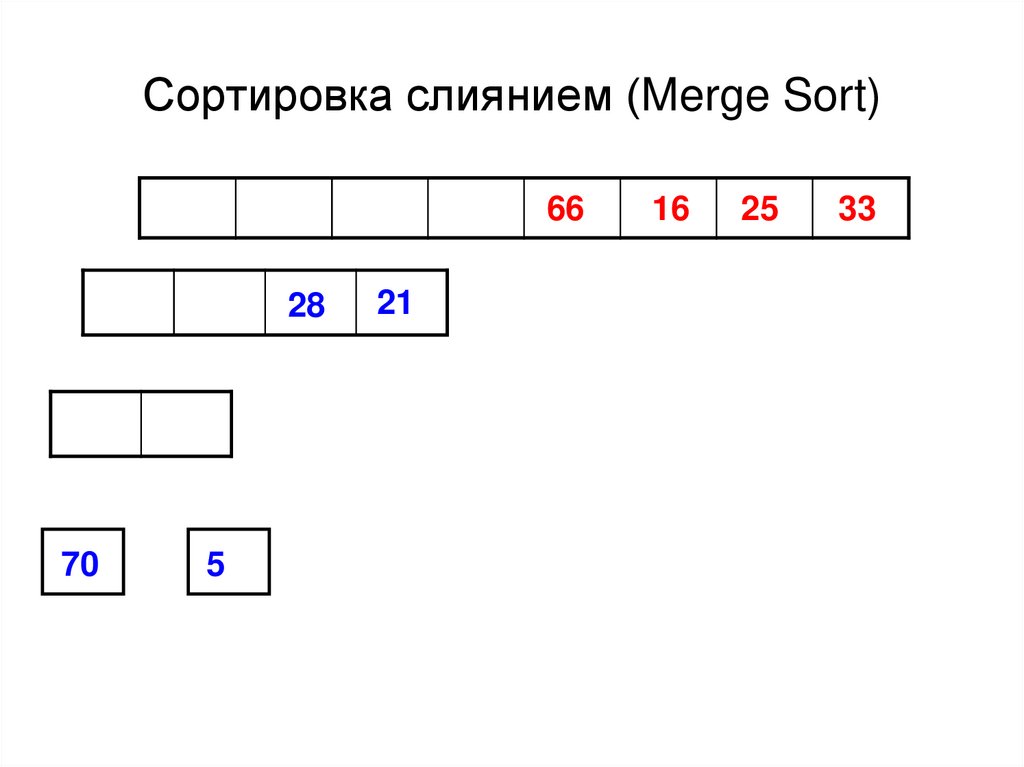
43. Сортировка слиянием (Merge Sort)

66
28
70
5
21
16
25
33

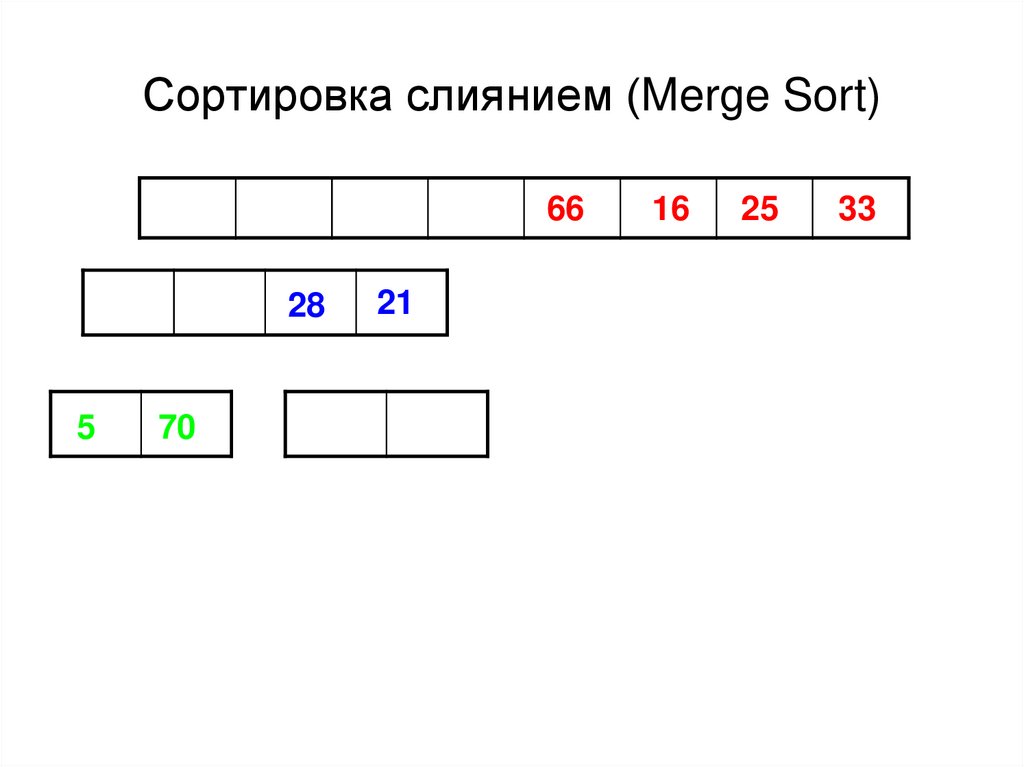
44. Сортировка слиянием (Merge Sort)

66
28
5
70
21
16
25
33

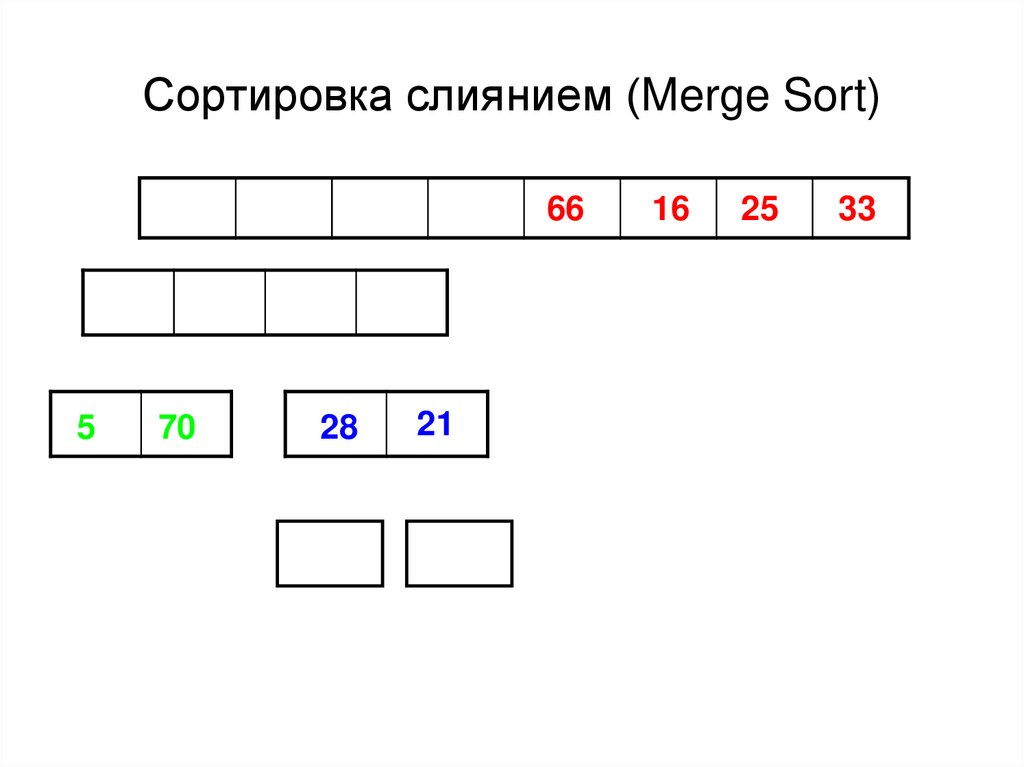
45. Сортировка слиянием (Merge Sort)

66
5
70
28
21
16
25
33

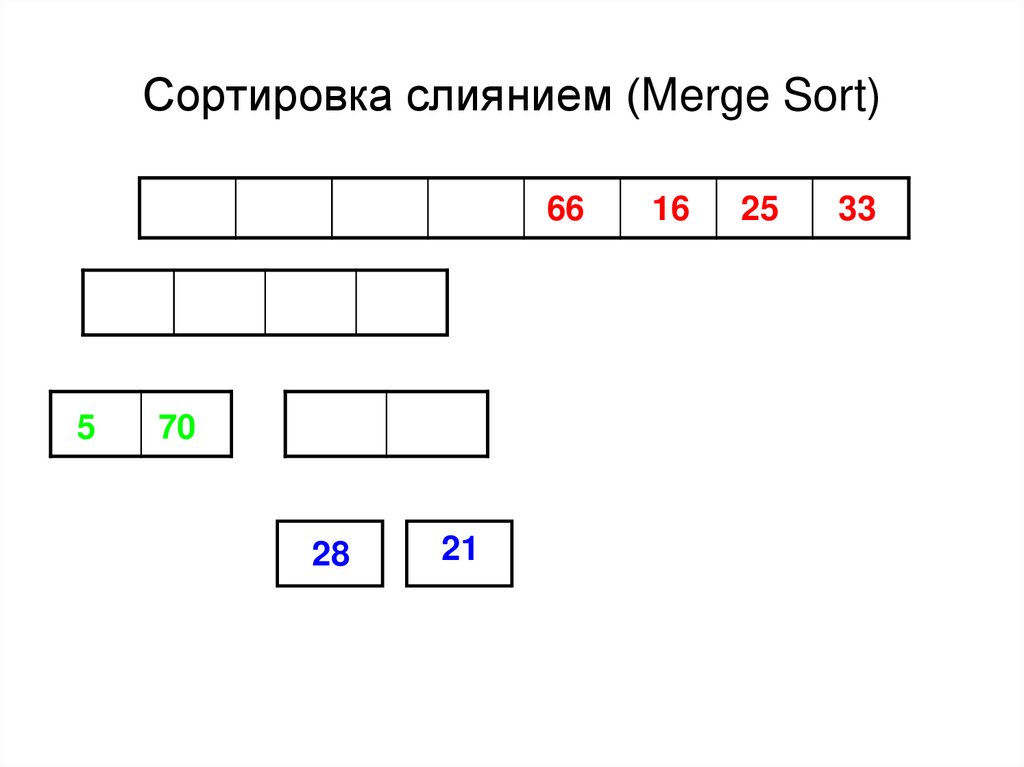
46. Сортировка слиянием (Merge Sort)

66
5
70
28
21
16
25
33

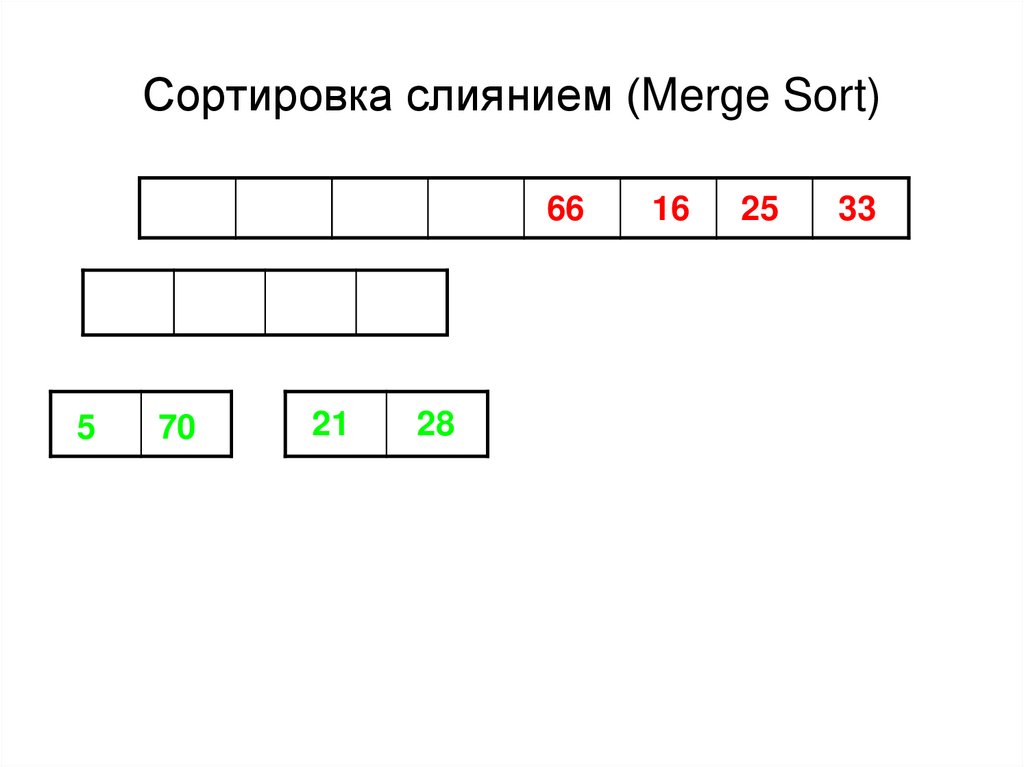
47. Сортировка слиянием (Merge Sort)

66
5
70
21
28
16
25
33

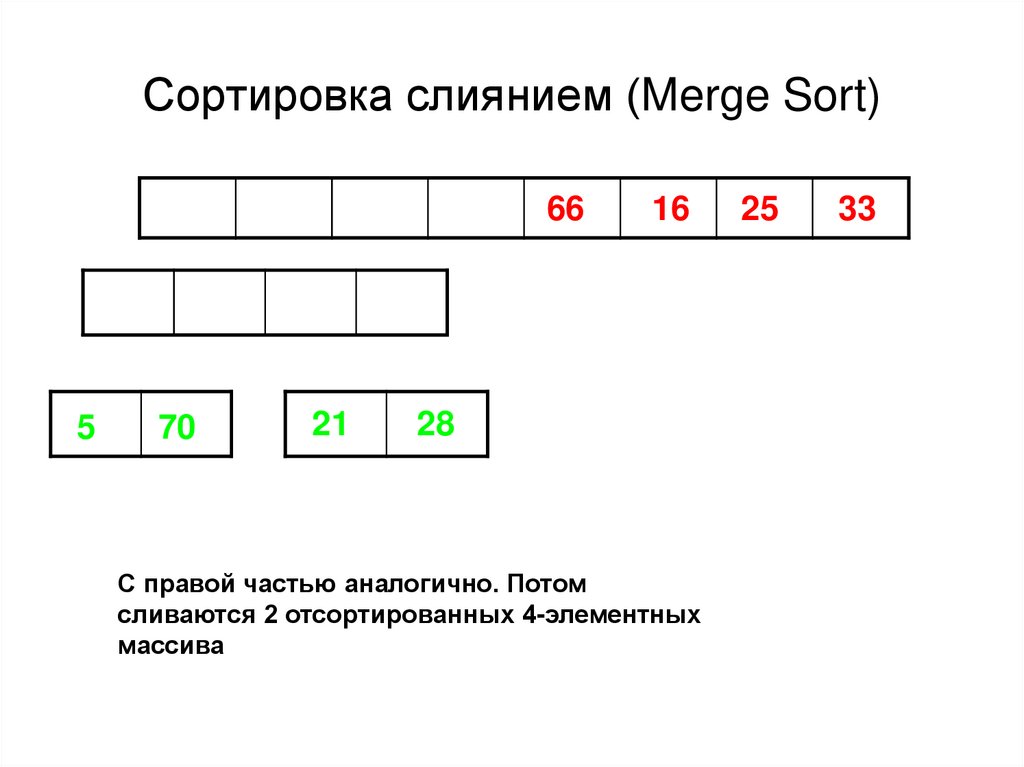
48. Сортировка слиянием (Merge Sort)

66
5
70
21
16
28
С правой частью аналогично. Потом
сливаются 2 отсортированных 4-элементных
массива
25
33

49.

• http://www.sorting-algorithms.com/mergesort

50. Быстрая сортировка

выбирается некоторый опорный элемент a[i],
запускается процедура разделения массива,
которая перемещает все ключи, меньшие, либо
равные a[i], влево от него, а все ключи, большие,
либо равные a[i] - вправо,
теперь массив состоит из двух подмножеств,
причем левое меньше, либо равно правого,
для обоих подмассивов: если в подмассиве более
двух элементов, рекурсивно запускаем для него
пункт 2.

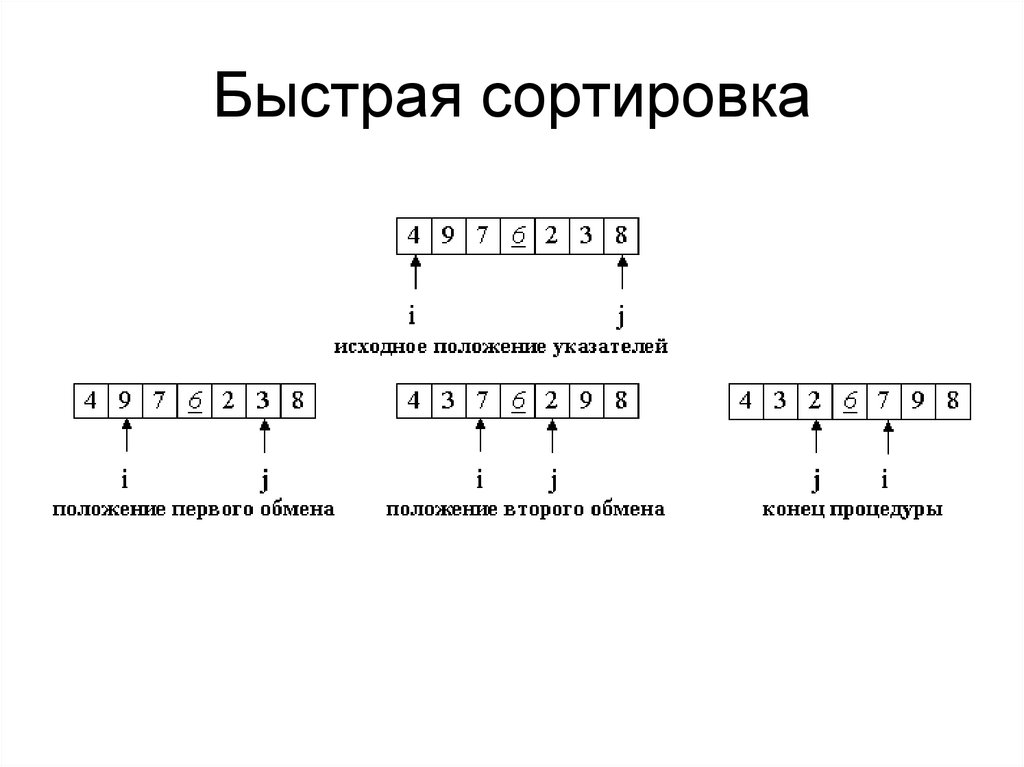
51. Быстрая сортировка

1. Введем два указателя: i и j.
2. Будем двигать указатель i с шагом в 1 элемент по
направлению к концу массива, пока не будет найден элемент
a[i] >= p. Аналогичным образом начнем двигать указатель j
от конца массива к началу, пока не будет найден a[j] <= p.
3. Далее, если i <= j, меняем a[i] и a[j] местами и
продолжаем двигать i,j по тем же правилам...
4. Повторяем шаг 3, пока i <= j.

52. Быстрая сортировка

53. Быстрая сортировка. Псевдокод

quickSort ( массив a, верхняя граница N )
{
Выбрать опорный элемент p - середину массива
Разделить массив по этому элементу
Если подмассив слева от p содержит более одного элемента,
вызвать quickSort для него.
Если подмассив справа от p содержит более одного элемента,
вызвать quickSort для него.
}

54. Быстрая сортировка

• http://www.sorting-algorithms.com/quicksort

55.

56. Сравнение методов сортировки С- число сравнений М-число пересылок

Min
Avg
Max
C = n-1
M = 2x(n-1)
(n2 + n - 2)/4
(n2 - 9n - 10)/4
(n2 -n)/2 - 1
(n2 -3n - 4)/2
C = (n2 - n)/2
Прямой выбор
M = 3x(n-1)
(n2 - n)/2
nx(ln n + 0.57)
(n2 - n)/2
n2/4 + 3x(n-1)
(n2 - n)/2
(n2 - n)x0.75
(n2 - n)/2
(n2 - n)x1.5
Прямое
включение
(вставка)
Прямой обмен
C = (n2 - n)/2
M=0

57.

Алгоритмы устойчивой сортировки
•Сортировка пузырьком (англ. Bubble sort )
•Сортировка перемешиванием (Шейкерная, Cocktail sort, bidirectional bubble
sort)
•Гномья сортировка
•Сортировка вставками (Insertion sort)
•Блочная сортировка (Корзинная сортировка, Bucket sort)
•Сортировка подсчётом (Counting sort)
•Сортировка слиянием (Merge sort)
•Сортировка с помощью двоичного дерева (англ. Tree sort)

58.

Алгоритмы неустойчивой сортировки
Сортировка выбором (Selection sort)
Сортировка Шелла (Shell sort)
Сортировка расчёской (Comb sort)
Пирамидальная сортировка (Сортировка кучи, Heapsort)
Плавная сортировка (Smoothsort)
Быстрая сортировка (Quicksort),
Introsort
Patience sorting
Stooge sort.
Поразрядная сортировка
Цифровая сортировка — то же, что и Поразрядная сортировка.

59. Внешние сортировки

60. Метод слияний

Упорядоченный отрезок (серия)
a(i), a(i+1), ..., a(j),
a(k) <= a(k+1)
для всех i <= k < j,
a(i-1) > a(i) и a(j) > a(j+1)
9345632

61.

1.
12 35 65 0 24 26 3 5 84 90 6 2 30
12 35 65 | 0 24 36 | 3 5 84 90 | 6 | 2 30 - 5 отрезков.
2.
1 2 3 4 5 6 7 8 9 10
| 1 2 3 4 5 6 7 8 9 10 | - 1 отрезок.
3.
20 17 16 14 13 10 9 8 6 4 3 2 0
| 20 | 17 | 16 | 14 | 13 | 10 | 9 | 8 | 6 | 4 | 3 | 2 | 0 | - 13 отрезков.

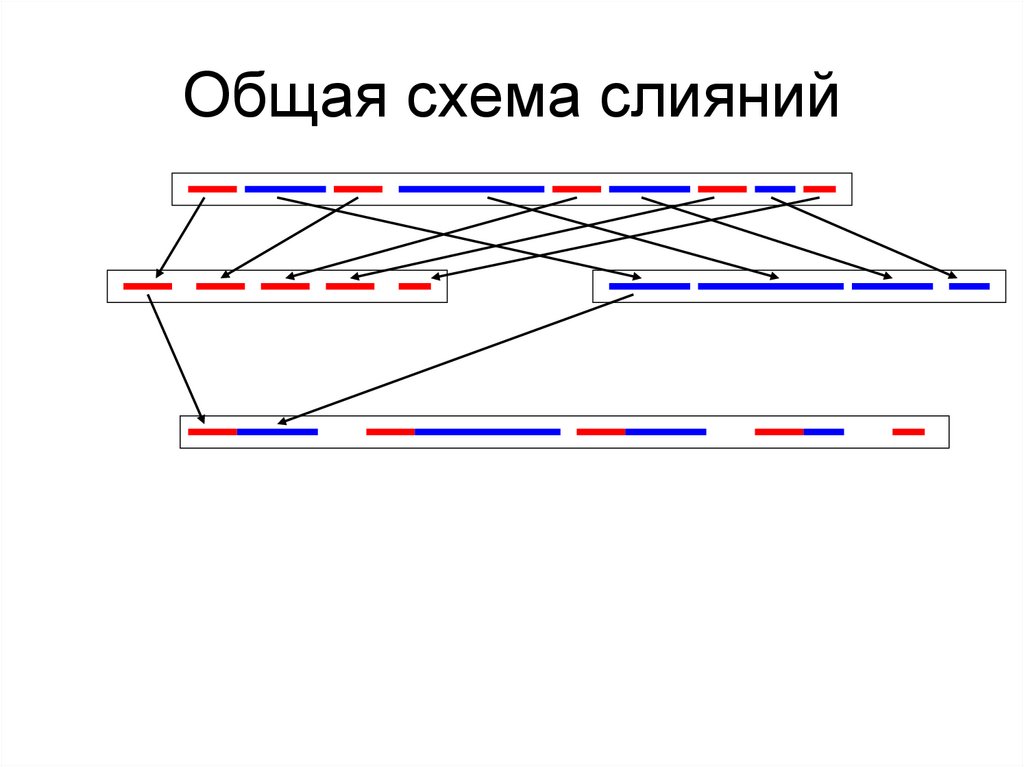
62. Общая схема слияний

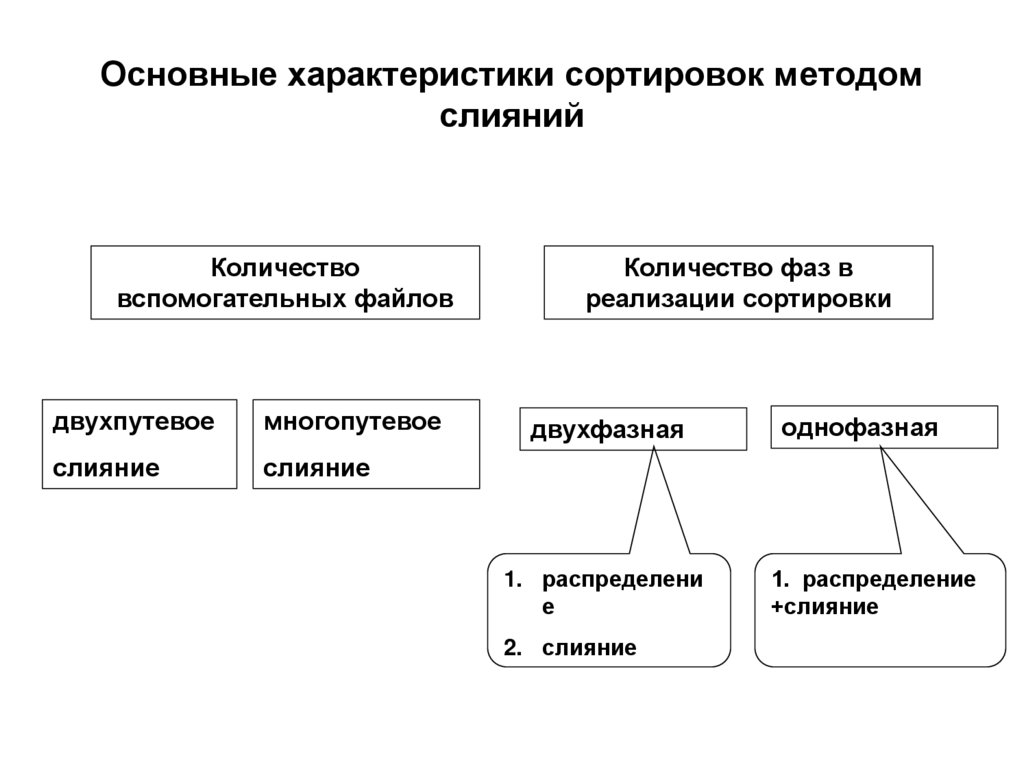
63. Основные характеристики сортировок методом слияний

Количество
вспомогательных файлов
двухпутевое
многопутевое
слияние
слияние
Количество фаз в
реализации сортировки
двухфазная
однофазная
1. распределени
е
1. распределение
+слияние
2. слияние

64. Простое (прямое слияние)

файл А,
a1,a2,….an
Вспомогательные файлы В и С
1. В В читаются элементы с нечетными индексами (a1,a3,..a(n-1))
2. В С читаются элементы с четными индексами (a2,a4,..a(n))
3. Файлы В и С сливаются в файл А: попарно а1 с а2, а3 с а4 и
т.д.
4. Обновленный файл А разбивается на В и С: в В идут
нечетные пары, в С – четные
5. Файлы В и С сливаются в А
6. А разбивается на В и С по четверкам и т.д.
7. Перед последним шагом файл A будет содержать две серии
размером n/2 каждая. Первая – в В, вторая – в С.
8. Сливаем в А. – получим упорядоченную последовательность
записей.

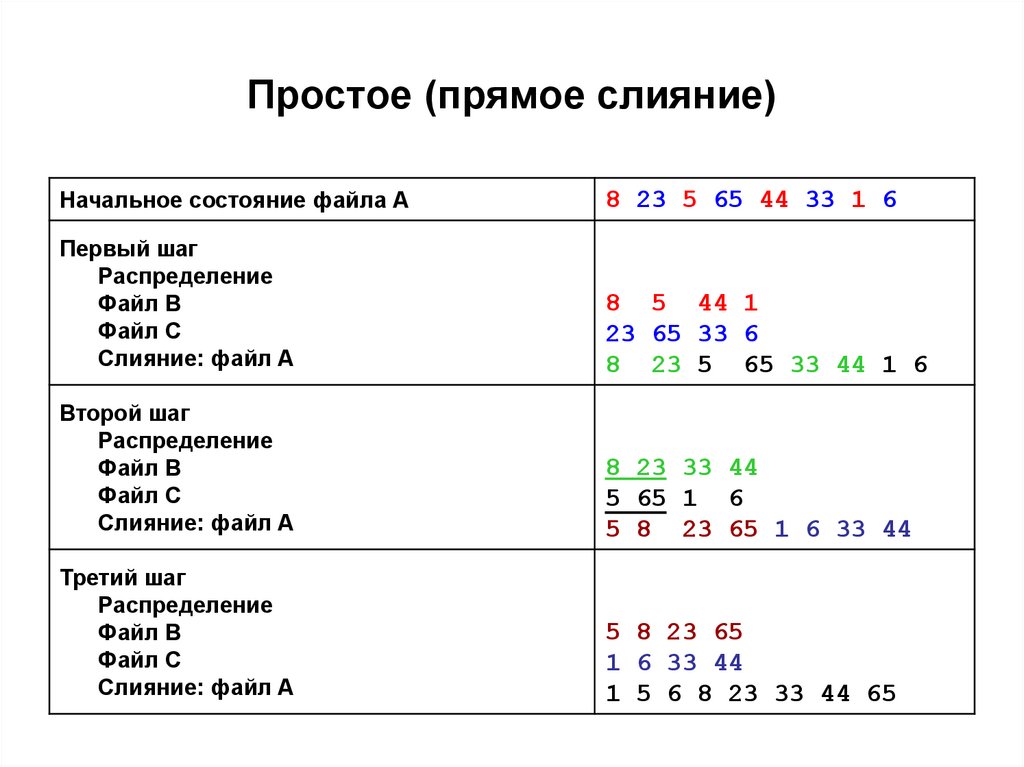
65. Простое (прямое слияние)

Начальное состояние файла A
8 23 5 65 44 33 1 6
Первый шаг
Распределение
Файл B
Файл C
Слияние: файл A
8 5 44 1
23 65 33 6
8 23 5 65 33 44 1 6
Второй шаг
Распределение
Файл B
Файл C
Слияние: файл A
8 23 33 44
5 65 1 6
5 8 23 65 1 6 33 44
Третий шаг
Распределение
Файл B
Файл C
Слияние: файл A
5 8 23 65
1 6 33 44
1 5 6 8 23 33 44 65

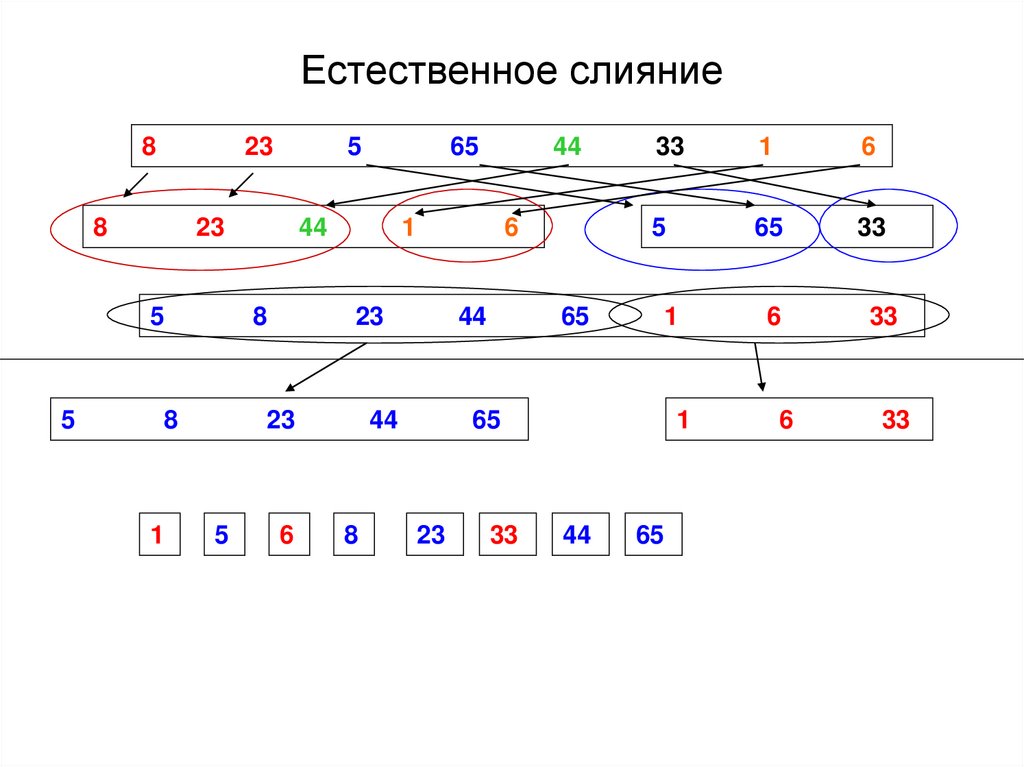
66. Естественное слияние

8
23
8
5
5
23
65
44
44
1
6
5
8
23
44
8
23
44
65
1
5
6
8
23
65
33
44
33
1
6
5
65
33
1
6
33
1
6
33
65

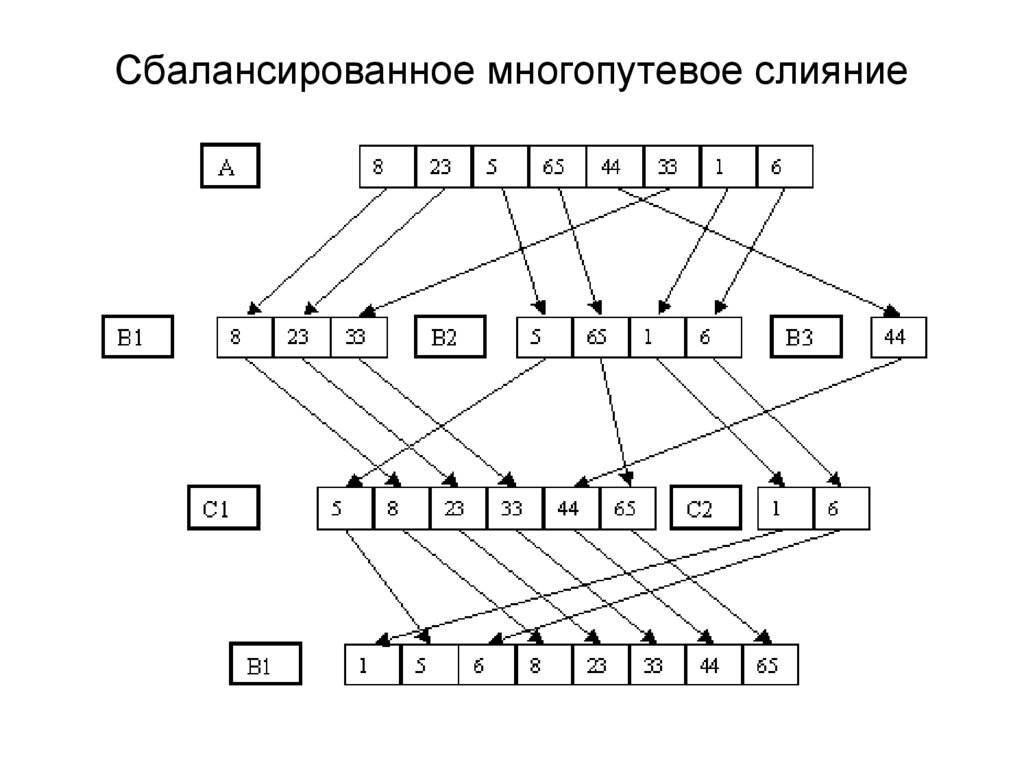
67. Сбалансированное многопутевое слияние

Исходный файл А – распределяется по m
вспомогательным B1,B2,…Bm
вспомогательные B1,B2,…Bm сливаются во
вспомогательные С1,С2,…Сm
С1,С2,…Сm сливаются в B1,B2,…Bm
и т.д.
пока в В1 или в С1 не образуется одна серия

68. Сбалансированное многопутевое слияние

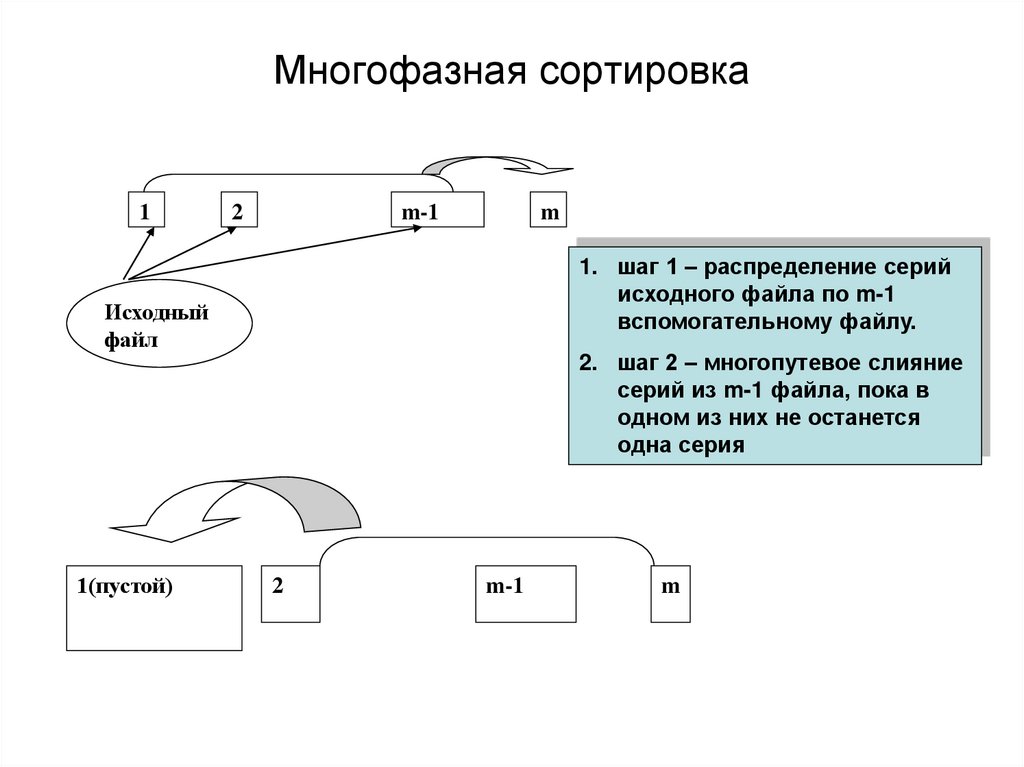
69. Многофазная сортировка

1
2
m-1
m
1. шаг 1 – распределение серий
исходного файла по m-1
вспомогательному файлу.
Исходный
файл
1(пустой)
2. шаг 2 – многопутевое слияние
серий из m-1 файла, пока в
одном из них не останется
одна серия
2
m-1
m

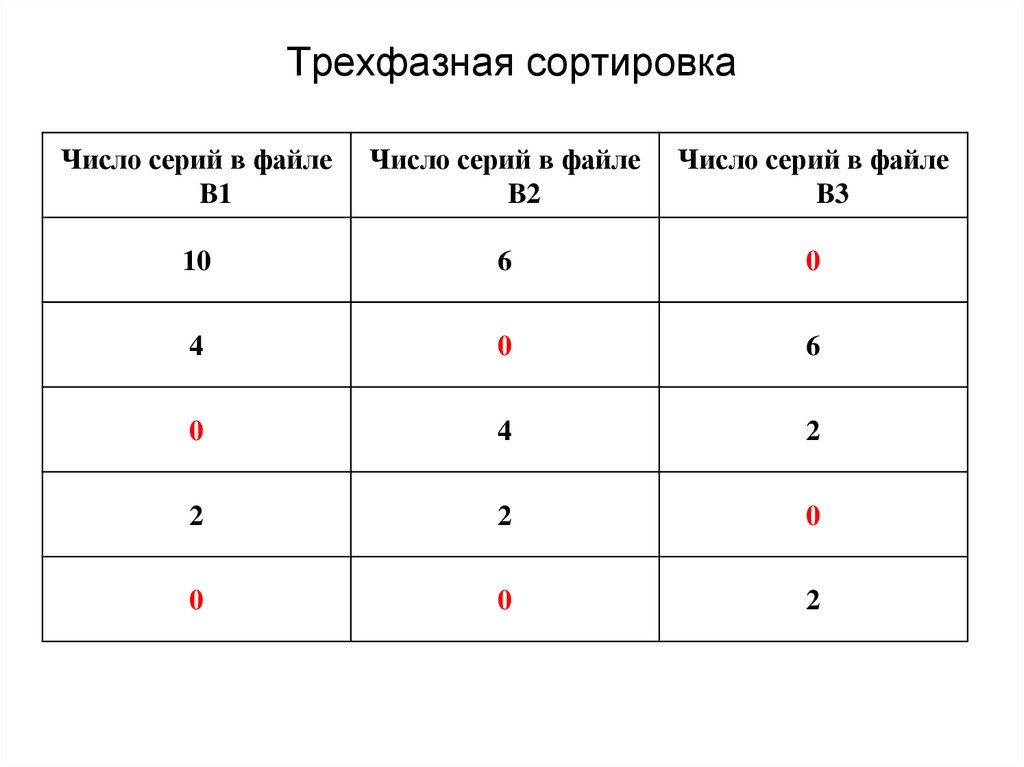
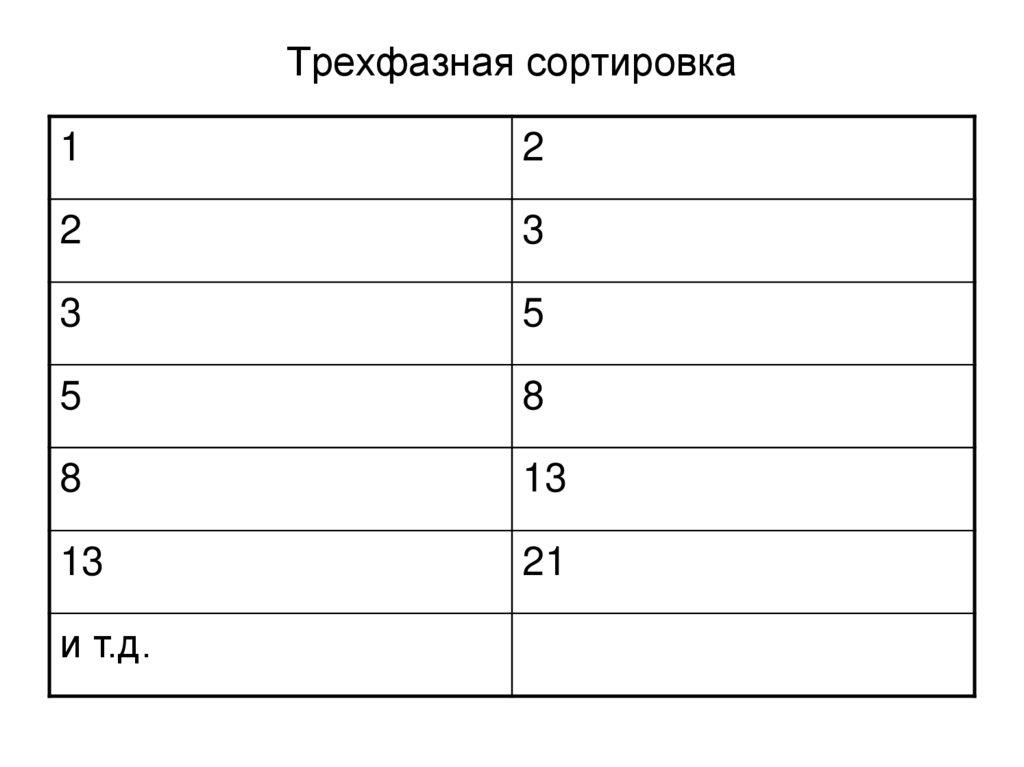
70. Трехфазная сортировка

Число серий в файле
B1
Число серий в файле
B2
Число серий в файле
B3
10
6
0
4
0
6
0
4
2
2
2
0
0
0
2

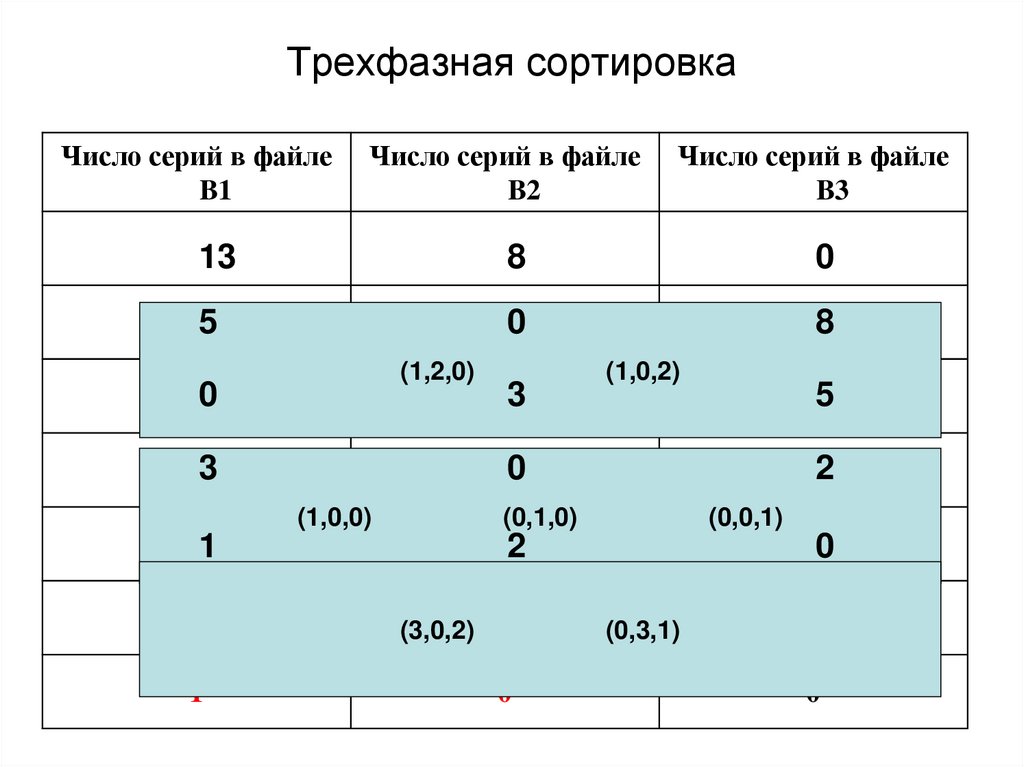
71. Трехфазная сортировка

Число серий в файле
B1
Число серий в файле
B2
Число серий в файле
B3
13
8
0
5
0
8
(1,2,0)
0
3
3
(1,0,2)
5
0
(1,0,0)
2
(0,1,0)
1
2
0
(3,0,2) 1
1
0
(0,0,1)
0
(0,3,1)
1
0

72. Трехфазная сортировка

1
2
2
3
3
5
5
8
8
13
13
21
и т.д.

73. Трехфазная сортировка

начало последовательности чисел Фибоначчи порядка 4:
(0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 31, 61, ...)
р=4
1. четыре нуля, р+1 элемент (пятый) равен 1– 0,0,0,0,1
2. 6-ой=сумме предыдущих пяти=0+0+0+0+1=1
3. 7-ой=сумме предыдущих пяти=0+0+0+1+1=2
4. 8-ой=сумме предыдущих пяти=0+0+1+1+2=4
5. 9-й=сумме предыдущих пяти=0+1+1+2+4=8
6. 10-ый=сумме предыдущих пяти=1+1+2+4+8=16
7. 11-ый=сумме предыдущих пяти=1+2+4+8+16=31
8. и т.д.

74. Спасибо за внимание!