Множество натуральных чисел. Полная и неполная индукция. Метод математической индукции

1.

Множество натуральных чисел.
Полная и неполная индукция.
Метод математической индукции
§1 Множество натуральных чисел
• Натура́льные чи́сла (естественные числа) —числа,
возникающие естественным образом при счёте (как
в смысле перечисления, так и в смысле исчисления).

2.

§1 Множество натуральных чисел
Существуют два подхода к определению натуральных чисел —
это числа, используемые при:
перечислении (нумеровании) предметов (первый,
второй, третий…) — подход, общепринятый в
большинстве стран мира
обозначении количества предметов (нет предметов, один
предмет, два предмета…) — подход принят в трудах Бурбаки, где
натуральные числа определяются как мощности конечных
множеств

3.

§1 Множество натуральных чисел
Николя́ Бурбаки́ (фр. Nicolas Bourbaki) — коллективный
псевдоним группы французских математиков (позднее в
нее вошли несколько иностранцев), созданной в 1935 году.
• Шарль Дени Бурбаки,
французский генерал, фамилия
которого была взята в качестве
псевдонима.
• Целью группы является
написание серии книг,
отражающих
современное состояние математики.

4.

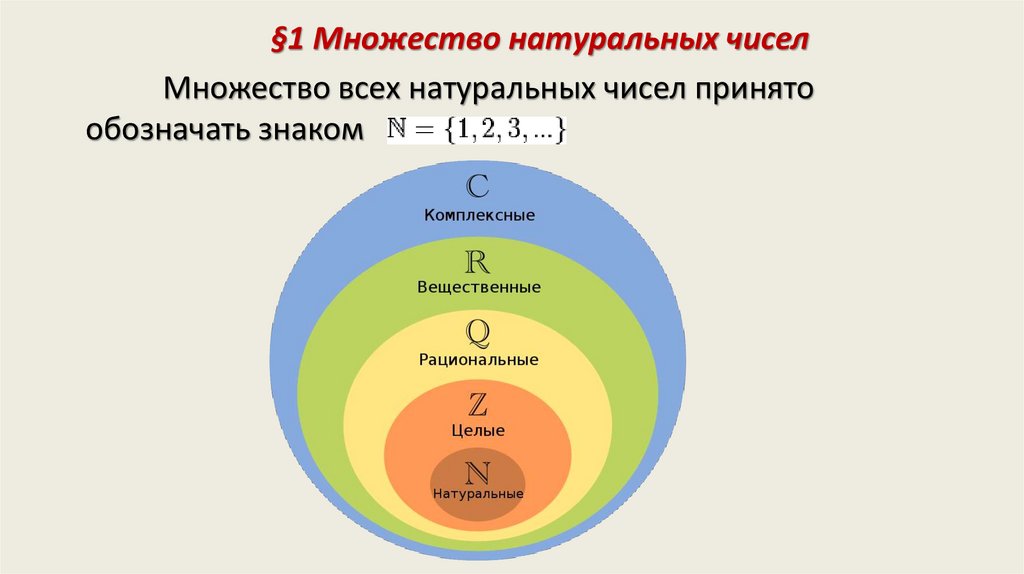
§1 Множество натуральных чисел
Множество всех натуральных чисел принято
обозначать знаком

5.

§1 Множество натуральных чисел
Чётность в теории чисел — характеристика целого числа,
определяющая его способность делиться нацело на два

6.

§1 Множество натуральных чисел

7.

§1 Множество натуральных чисел
Множество натуральных чисел описывается
с помощью системы аксиом Пеано, которые служат
аксиоматическим определением трёх исходных
(основных) понятий теории натуральных чисел:
«натуральное число»
«единица»
«непосредственно следует за»

8.

§1 Множество натуральных чисел
Джузе́ппе Пеа́но (итал. Giuseppe Peano ; 27 августа
1858 — 20 апреля 1932) — итальянский математик.
• Внёс вклад в математическую логику, аксиоматику,
философию математики.
• Создатель вспомогательного искусственного
языка латино-сине-флексионе.
• Более всего известен как автор стандартной
аксиоматизации натуральной арифметики —
арифметики Пеано.
• Автор более 200 книг и статей, он был одним из
основателей математической логики и теории
множеств.

9.

§1 Множество натуральных чисел
Множеством натуральных чисел называется
всякое непустое множество N , в котором для некоторых
элементов a и b существует отношение
«b непосредственно следует за а» (а, а’),
удовлетворяющее следующим аксиомам (аксиомам
Пеано):
1.Существует натуральное число 1, непосредственно не
следующее ни за каким натуральным числом, т.е. а’ ≠1.
2. Для любого натурального числа а существует одно и
только одно непосредственно следующее натуральное
число а’ , т.е. из равенства а= b следует равенство а’= b’.

10.

§1 Множество натуральных чисел
3. Любое натуральное число, кроме 1,
непосредственно следует за одним и только одним
натуральным число, т.е., если а’ ≠1, то из равенства
а’= b’ следует равенство а=b.
4. (Аксиома математической индукции)
Пусть М – множество натуральных чисел, обладающих
свойствами:
1) 1 ϵ М
2) если натуральное число а ϵ М, то и а’ ϵ М,
тогда множество М содержит все натуральные числа,
т.е. совпадает с М.

11.

§1 Множество натуральных чисел
• Натуральные числа 2, 3, 4 и т.д. можно определить.
• Натуральное число 2 – это число, которое
непосредственно следует за числом 1.
• Натуральное число 3 – это число, которое
непосредственно следует за числом 2 и т.д.
• По определению:
2=1’,
3=2’,
100=99’

12.

§1 Множество натуральных чисел
• Натуральные числа замкнуты относительно
сложения и умножения (но не вычитания или
деления).
• Натуральные числа коммутативны и
ассоциативны относительно сложения и
умножения, а умножение натуральных чисел
дистрибутивно относительно сложения:
a + b = b + a,
(a + b) + c = a + (b + c),
(a + b) · c = a · c + b · c

13.

§2 Индукция как метод научного исследования
В основе всякого математического исследования
лежат дедуктивный и индуктивный методы.
Дедуктивный метод рассуждений - это рассуждение
от общего к частному, т.е. рассуждение, исходным
моментом которого является общий результат,
а заключительным моментом – частный результат.
Индукция применяется при переходе от частных
результатов к общим, т.е. является методом,
противоположным дедуктивному.

14.

§2 Индукция как метод научного исследования
По своему первоначальному смыслу слово
«индукция» применяется к рассуждениям, при
помощи которых получают общие выводы, опираясь
на ряд частных утверждений.
Простейшим методом рассуждений такого рода
является полная индукция.

15.

§2 Индукция как метод научного исследования
Пусть требуется установить, что каждое
натуральное чётное число n в пределах 4< n < 20
представимо в виде суммы двух простых чисел.
Для этого возьмём все такие числа и выпишем
соответствующие разложения:
4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;
14=7+7; 16=11+5; 18=13+5; 20=13+7.

16.

§2 Индукция как метод научного исследования
Эти девять равенств показывают, что каждое из
интересующих нас чисел, действительно,
представляется в виде суммы двух простых слагаемых.
Такое рассуждение является доказательством.
Таким образом, полная индукция заключается
в том, что общее утверждение доказывается
по отдельности в каждом из конечного числа
возможных случаев.

17.

§2 Индукция как метод научного исследования
Иногда общий результат удаётся предугадать после
рассмотрения не всех, а достаточно большого числа
частных случаев (так называемая неполная индукция).
Результат, полученный неполной индукцией,
остается, однако, лишь гипотезой, пока он не доказан
точным математическим рассуждением, охватывающим
все частные случаи.
Иными словами, неполная индукция в математике
не считается законным методом строгого доказательства,
но является мощным методом открытия новых истин.

18.

§2 Индукция как метод научного исследования
Пример. Найти сумму первых n последовательных нечётных чисел.
Рассмотрим частные случаи:
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
После рассмотрения этих нескольких частных случаев
напрашивается следующий общий вывод:
1+3+5+…+(2n-1)=