Определение длины световой волны при помощи дифракционной решетки

1.

ЛАБОРАТОРНАЯ РАБОТА
ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ
ВОЛНЫ ПРИ ПОМОЩИ
ДИФРАКЦИОННОЙ РЕШЕТКИ
кафедра ОПФ МГСУ

2.

Дифракция света
Явление огибания волнами препятствий и попадания света в область
геометрической тени называется дифракцией света.
Опыт Юнга, благодаря которому изучалась интерференция света,
одновременно был опытом, демонстрирующим дифракцию, так как из
щелей или отверстий выходили не узкие лучи света, а расширяющиеся
пучки, что свидетельствует об отклонении света от прямолинейного
распространения при малых размерах препятствий, в нашем случае
щелей.
Дифракция неразрывно связана с интерференцией.

3.

Явление дифракции можно объяснить, используя принцип Гюйгенса–
Френеля, который формулируется следующим образом: каждая точка
волнового фронта является источником вторичных волн, причем все эти
вторичные источники когерентны.
Огибающая
к фронтам волн от вторичных источников дает положение
нового фронта волны. Все вторичные источники когерентны, и распределение
интенсивности есть результат интерференции волн, излучаемых вторичными
источниками.
Цель работы – изучение дифракции света и определение длины волны на
основе этого явления

4.

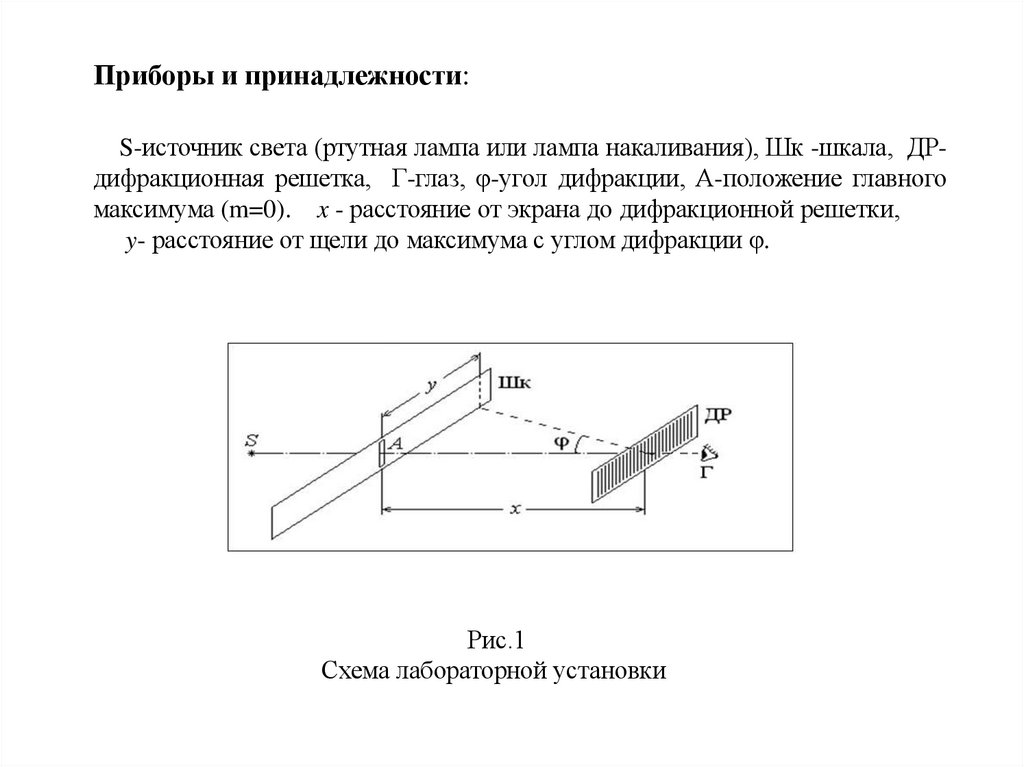
Приборы и принадлежности:
S-источник света (ртутная лампа или лампа накаливания), Шк -шкала, ДРдифракционная решетка, Г-глаз, φ-угол дифракции, А-положение главного
максимума (m=0). x - расстояние от экрана до дифракционной решетки,
y- расстояние от щели до максимума с углом дифракции φ.
Рис.1
Схема лабораторной установки

5.

Теория опыта
Дифракционная решетка представляет собой ряд параллельных очень
узких
щелей,
разделённых
одинаковыми
непрозрачными
промежутками, нанесенных на прозрачную пластинку.
Сумма ширины щели b и ширины непрозрачной полосы а называется
периодом дифракционной решетки d:
d = a + b.
Способность дифракционной решётки разлагать свет в спектр
используют на практике для исследования спектров и определения
излучателя, например, состава смеси газов.
Дифракционная картина при дифракции
на решетке является
результатом интерференции волн от всех щелей решетки.

6.

.
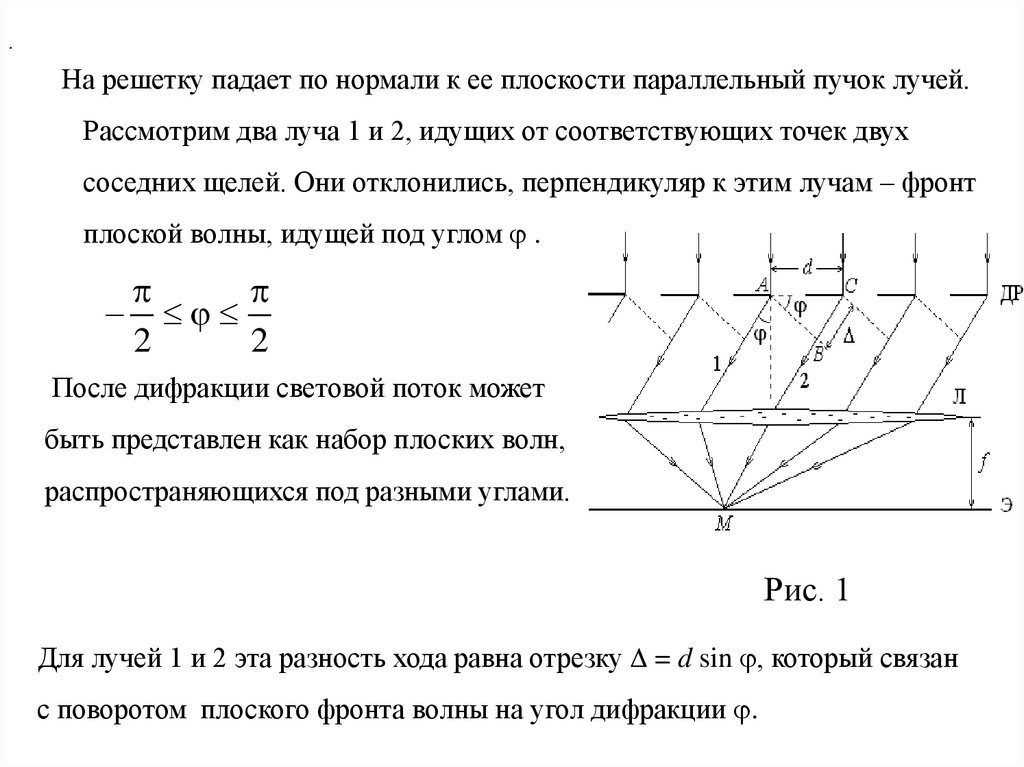
На решетку падает по нормали к ее плоскости параллельный пучок лучей.
Рассмотрим два луча 1 и 2, идущих от соответствующих точек двух
соседних щелей. Они отклонились, перпендикуляр к этим лучам – фронт
плоской волны, идущей под углом .
2
2
После дифракции световой поток может
быть представлен как набор плоских волн,
распространяющихся под разными углами.
Рис. 1
Для лучей 1 и 2 эта разность хода равна отрезку = d sin , который связан
с поворотом плоского фронта волны на угол дифракции .

7.

Если разность хода волн от соседних щелей соответствует максимуму
интерференции
d sin = m , где где m = 0, ±1, ±2, ±3…
(1)
то на экране мы увидим светлую полосу.
На экране будут видны чередующиеся светлые и темные полосы, если источник
света монохроматический.
При облучении дифракционной решетки белым светом, центральная полоса на
экране (m = 0) будет белой (спектр нулевого порядка). d sin = 0 ,
Спектры других порядков будут расположены симметрично относительно спектра
нулевого порядка.
В каждом из этих спектров фиолетовая линия будет расположена ближе к центру,
наиболее удаленной – красная.
.

8.

При увеличении числа щелей N при d=const помимо роста
интенсивности (I =I0N ) происходит резкое сужение главных
максимумов, в результате чего расплывчатые максимумы
превращаются в узкие, разделенные темными промежутками.
Рис. 4
Распределение интенсивности монохроматического
излучения. Пунктирная линия соответствует
дифракции на одной щели дифракционной решетки.
Третий порядок дифракции имеет низкую
интенсивность, поскольку ширина щели равна трети
периода.

9.

На рис.3 показано расположение дифракционных максимумов
при освещении дифракционной решетки белым светом
В центре наблюдается белая линия - максимум
нулевого порядка. По обе стороны от нее расположены спектры
различных порядков – цифры вверху графика.
Спектр третьего порядка изображен пунктиром, поскольку в реальной
решетке ширина щели (b) составляет треть ширины периода (d) и
интенсивность спектра третьего порядка очень низкая.
Рис.3

10.

При увеличении числа щелей дифракционной решетки N:
а) расположение главных максимумов на экране не меняется;
б) число главных максимумов остается равным (2d/λ+1), т.е
(2N+1);
в) угловая ширина главных максимумов уменьшается:
Δφ = λ/Nd
(энергия перераспределяется в главные
максимумы);
г) интенсивность главных максимумов увеличивается;
д) число дополнительных минимумов между соседними
главными максимумами, равное (N-1), увеличивается;
е) число вторичных максимумов между двумя соседними
главными максимумами, равное (N-2), увеличивается.

11.

Исследуются
Вывод рабочей формулы
спектры
не
выше
третьего
порядка,
для
используемой
дифракционной решётки. Углы дифракции для первого порядка дифракции
малы, в связи с чем их синусы можно заменить тангенсами. В свою очередь,
тангенс угла , как видно из рис.1, равен отношению y/x, где y – расстояние от
щели A до мнимого изображения спектральной линии на шкале, а x –
расстояние от шкалы до решётки. Таким образом,
y
sin tg
x
Тогда вместо формулы (1) будем иметь уd/х =mλ, откуда
λ=уd/mx
(2)
Для линий второго порядка дифракции следует выполнить преобразование