Предикаты. Понятие предиката

1. ПРЕДИКАТЫ

2. 1. Понятие предиката

В логике предикатов элементарное
высказывание разделяется на две
части: субъект (буквально —
подлежащее, хоть эта часть может
играть роль дополнения) и
предикат (буквально - сказуемое,
но эта часть может играть и роль
определения).

3.

Субъект — это то, о чем что-то
утверждается в высказывании;
предикат - это то, что утверждается
о субъекте.

4. Пример:

В высказывании «7 - простое число», «7» -субъект,
«простое число» - предикат. Это высказывание
утверждает, что «7» обладает свойством «быть
простым числом».
Если в рассмотренном примере заменить конкретное
число 7 переменной х из множества натуральных
чисел, то получим высказывательную форму «х простое
число».
При
одних
значениях
х,
(например, х = 13, х =17 ) эта форма дает
истинные высказывания, а при других значениях х
(например, х = 10 , х = 18 ) эта форма дает
ложные высказывания.

5.

Одноместным предикатом Р(х)
называется произвольная функция
переменного х, определенная на
множестве М и принимающая
значения из множества {1,0}.

6.

Множество М, на котором определен
предикат P(х) , называется
областью определения предиката.

7.

Множество всех элементов х М ,
при которых предикат принимает
значение «истина», называется
множеством истинности предиката
Р(х).

8. Примеры:

Р(х) - «х - простое число» определен на
множестве N, а множество истинности для
него есть множество всех простых чисел.
Предикат Q{x} - «sin х = 0» определен на
множестве R, а его множество истинности множество чисел πn, nϵN.
Предикат F(x) - «Диагонали
параллелограмма перпендикулярны»
определен на множестве всех
параллелограммов, а его множеством
истинности является множество всех ромбов.

9.

Предикат Р(х), определенный на
множестве
М,
называется
тождественно
истинным
,если
область определения предиката и
область истинности совпадают.

10. 2. Логические операции над предикатами

Предикаты,
так
же,
как
высказывания,
принимают
два
значения истина и ложь (1, 0),
поэтому к ним применимы все
операции логики высказываний.

11. Пример 1.

На множестве М = (3,4,5,6,7,8)
заданы два предиката P(х): «х —
простое число», Q(x): «х —
нечетное число». Составьте их
таблицы принадлежности.
Равносильны ли предикаты Р(х) и
Q(x) на множествах L = {2, 3,4, 5,
6, 7, 8} и К = {3, 4, 5, 6, 7, 8, 9}?

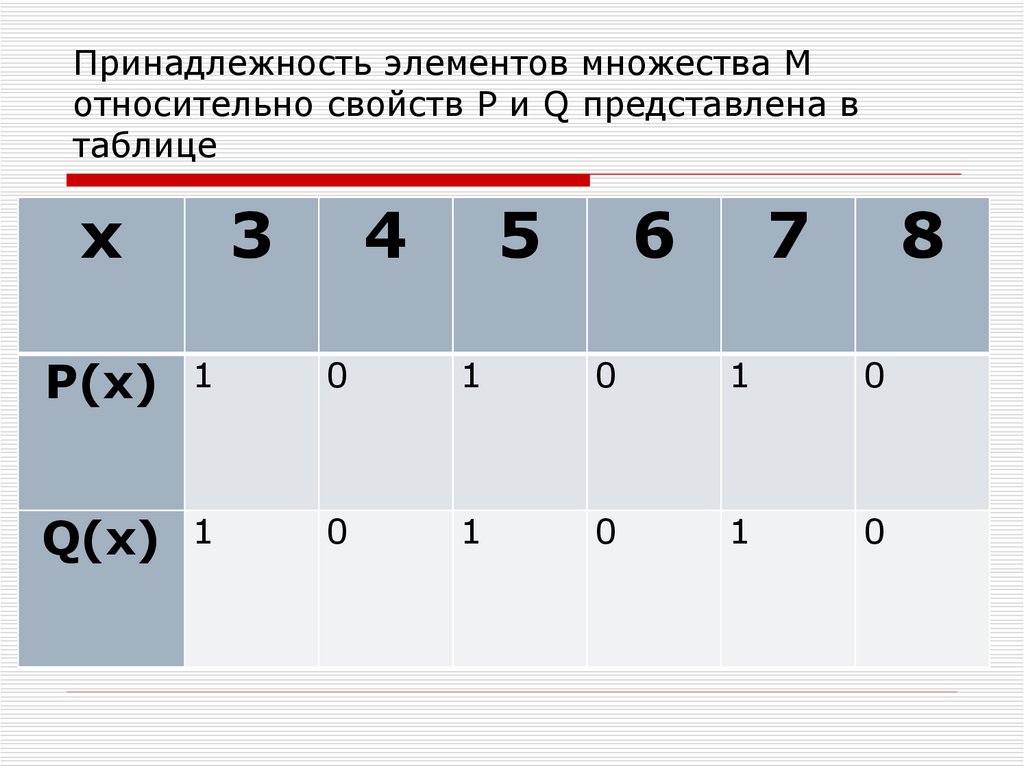
12. Принадлежность элементов множества М относительно свойств P и Q представлена в таблице

x
P(x)
3
4
5
6
7
8
1
0
1
0
1
0
Q(x) 1
0
1
0
1
0

13. Равносильны ли предикаты Р(х) и Q(x) на множествах L = {2, 3,4, 5, 6, 7, 8} и К = {3, 4, 5, 6, 7, 8, 9}?

x 2
3
4
5
6
7
8
4
5
6
7
8
9
P(x)
Q(x)
x 3
P(x)
Q(x)

14.

Конъюнкцией двух предикатов Р(х)
и Q(x) называется новый предикат
Р(х) Q{x), который принимает
значение «истина» при тех и только
тех значениях х М, при которых
каждый из предикатов принимает
значение «истина», и принимает
значение «ложь» во всех остальных
случаях.

15. Пример:

Для предикатов Р(х): «х – четное
число» и Q(x): «х кратно 3»
конъюнкцией P(x) Q(x) является
предикат «х - четное число и х
кратно 3», то есть предикат «х
делится на 6»

16.

Дизъюнкцией двух предикатов Р(х)
и Q(x) называется новый предикат
Р(х)V Q(x), который принимает
значение «ложь» при тех и только
тех значениях х М, при которых
каждый из предикатов принимает
значение «ложь» и принимает
значение «истина» во всех
остальных случаях.

17.

Отрицанием
предиката
Р(х)
называется
новый
предикат
,
который
принимает
значение
«истина» при всех значениях х М,
при
которых
предикат
Р(х)
принимает значение «ложь», и
принимает значение «ложь» при тех
значениях х М, при которых
предикат Р(х) принимает значение
«истина».

18.

Импликацией Р(х) и Q(x)
называется новый предикат Р(х) и
Q(x), который является ложным при
тех и только тех значениях х ∈ М,
при которых одновременно Р(х)
принимает значение «истина», а
Q(x) — значение «ложь», и
принимает истинное значение во
всех остальных случаях.

19. Пример 2.

На множестве М = {l, 2, 3, ..., 20} заданы
предикаты:
А(х): «х не делится на 5»,
В(х): «х — четное число»,
С(х): «х — число простое»,
D(x): «х кратно трем».
Найдите множества истинности
предикатов:
1) А(х) ∧ В(х) ∧ D(х)
2) A(x) ∨ B(x)
3) D(x) → ¬C(x).

20. 1) А(х) ∧ В(х) ∧ D(х)

А(х): «х не делится на 5»,
В(х): «х — четное число»,
D(x): «х кратно трем».
А(х) ∧ В(х) ∧ D(х) = {х не делится
на 5 и х — четное число и х кратно
трем} = {х не делится на 5 и х
делится на 6}.
Ip= {6, 12, 18}.

21.

2. A(x) ∨ B(x) = {х не делится на 5
или х — четное число}. Ip = М – {5,
15}.
3. D(x) → ¬C(x) = ¬D(x) ∨ ¬C(x) =
{х не кратно трем или х —
непростое число}. Если перебрать
все элементы множества М, то легко
установить, что Ip = М — {3}.

22. Задание 1

Для следующих предложений
выделить предикаты и для каждого
из них указать область истинности:
х+5=1;
х+2<3x – 4;
однозначное число х кратно 3;

23. Задание 2

Изобразить на декартовой
плоскости области истинности
предикатов:
х+у=1;
х+3у=3;
((x>2)v(y>1))((x<-1)v(y<-2)).