Лекция 1. Элементы математической логики

1.

Прикладная математика и
математическая логика
(2 семестр)
План:
1. Лекции (16 пар)
2. Практические занятия (16 пар)
3. Экзамен
Солдатова Гульнара Тагировна 1-306
Таймлайн- Диалоги
gulnara.soldatova@rsvpu.ru

2.

Разделы
1. Элементы математической логики
2. Интегральное исчисление функций одной переменной и его
приложения
3. Числовые и функциональные ряды. Элементы функционального
анализа
4. Дифференциальные уравнения.
5. Дифференциальное исчисление функций нескольких переменных
6. Векторный анализ, элементы теории поля
7. Элементы теории вероятностей и математической статистики

3.

БРС
1. Домашние работы
2. Проверочные работы
3. Конспект лекций
4. Участие в научных мероприятиях
Допуск к зачету -45 баллов.

4.

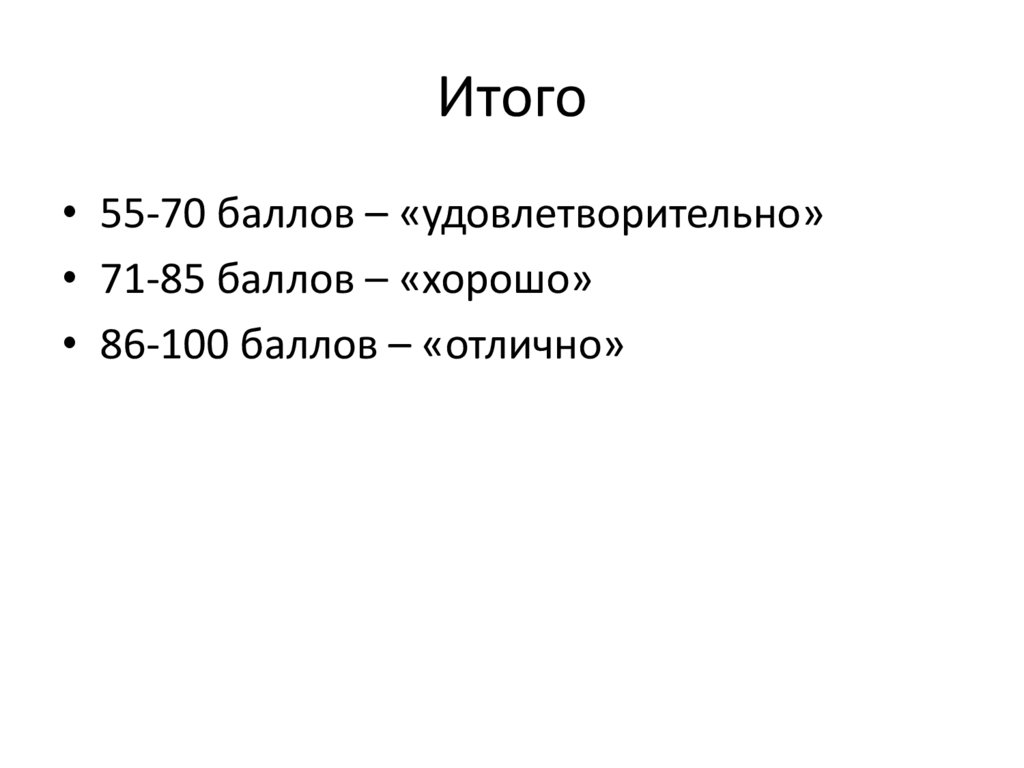
Итого
• 55-70 баллов – «удовлетворительно»
• 71-85 баллов – «хорошо»
• 86-100 баллов – «отлично»

5.

Лекция 1. Элементы
математической логики
1.
2.
3.
План:
Высказывание
Логические операции
Формулы

6.

• Математическая логика – часть логики, в
которой для решения логических задач
используются математические методы.

7.

• Математическая логика позволяет
проверять правильность рассуждений
механически, абстрагируясь от их смысла.
• Правильное рассуждение – то, которое
соответствует законам логики.
• Формализация рассуждения необходима,
например, в компьютерных программах.

8.

Алгебра логики (алгебра высказываний, булева алгебра) –
раздел математической логики, изучающий строение
(форму, структуру) сложных логических высказываний и
способы установления их истинности с помощью
математических методов.
Высказывание – повествовательное
предложение, содержание которого можно
определить как истинное или ложное.

9.

Примеры
1. Число 10 делится нацело на 2 и на 5
2. Париж – столица Италии
3. Да здравствует чемпион!
4. Сколько сегодня пар?

10.

Различают :
• Простые высказывания (обозначают буквами
латинского алфавита)
• Сложные (составные) высказывания

11.

Логическими
значениями
высказываний
являются «истина» и «ложь» и обозначают {0,1}
или {true, false}.

12.

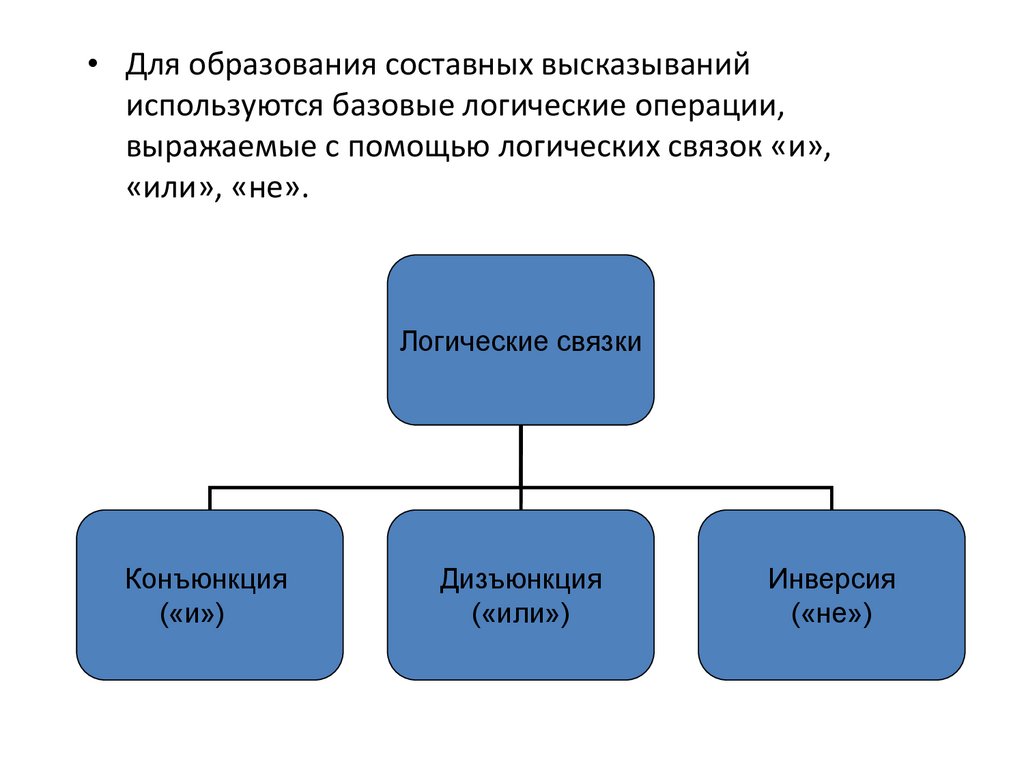
• Для образования составных высказываний
используются базовые логические операции,
выражаемые с помощью логических связок «и»,
«или», «не».
Логические связки
Конъюнкция
(«и»)
Дизъюнкция
(«или»)
Инверсия
(«не»)

13.

Логические операции
1. Логическое умножение (конъюнкция).
• Объединение двух (или нескольких) высказываний
в одно с помощью союза «и» называется операцией
логического умножения или конъюнкцией.
А
0
0
1
1
В
0
1
0
1
А˄В
0
0
0
1
Пример.
А: «12 делится на 3»
В: «12 делится на 4»,
Тогда А˄В - истинно

14.

2.Логическое сложение (дизъюнкция)
• Объединение двух (или нескольких)
высказываний с помощью союза «или»
называется операцией логического
сложения или дизъюнкцией.
А
0
0
1
1
В
0
1
0
1
А˅В
0
1
1
1
Пример.
А: «12 делится на 3»
В: «12 делится на 5»,
Тогда А ˅ В - истинно

15.

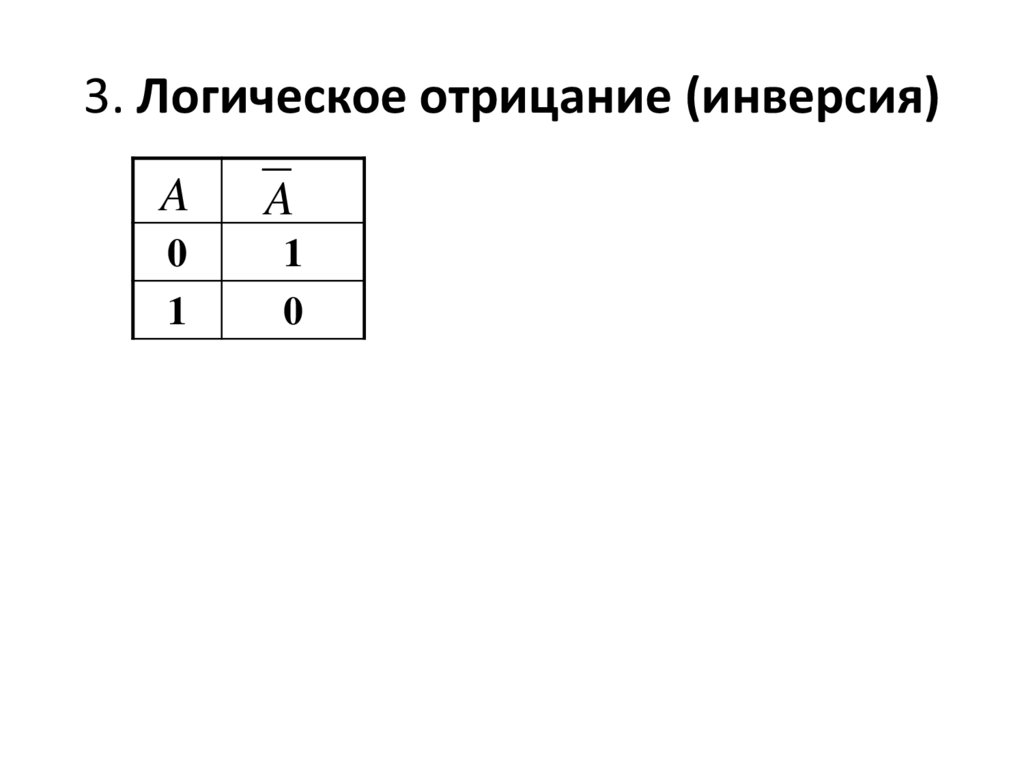
3. Логическое отрицание (инверсия)
A
A
0
1
1
0

16.

4. Импликация
Логическая связка: «ЕСЛИ …,
ТО», «ИЗ … СЛЕДУЕТ», «… ВЛЕЧЕТ
…».
Пример.
А: «студент усердно готовится к
экзамену»
В: «студент получает 5»,
Тогда А → В - истинно
А
0
0
1
1
В
0
1
0
1
А→В
1
1
0
1

17.

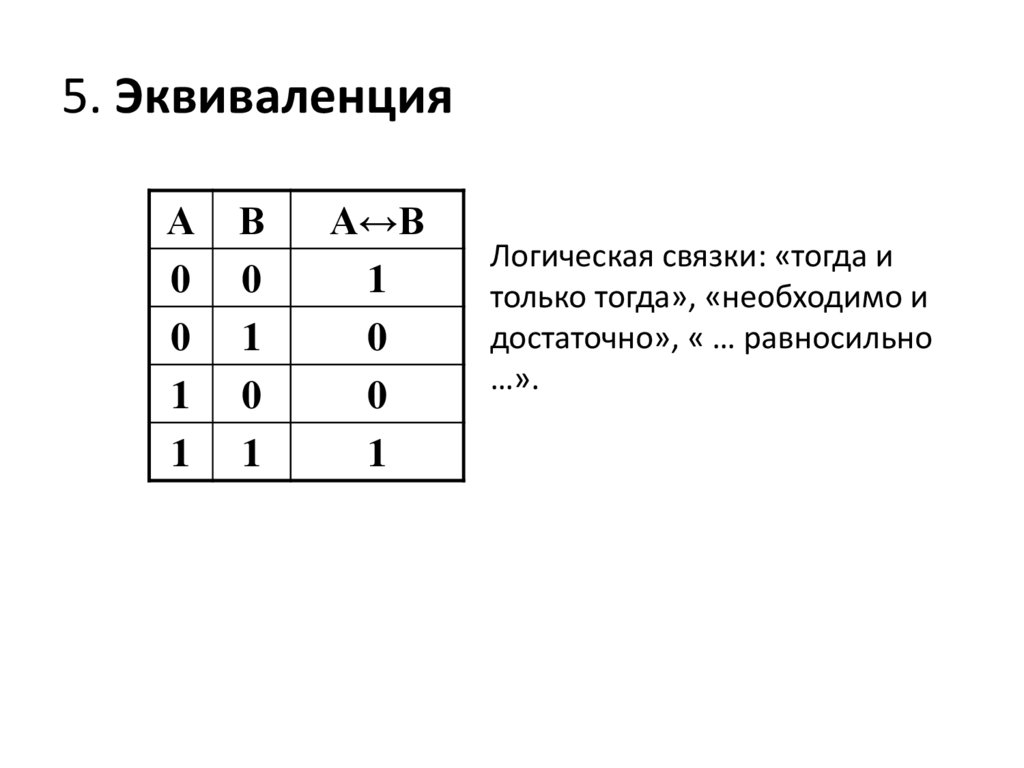
5. Эквиваленция
А
0
0
1
1
В
0
1
0
1
А↔В
1
0
0
1
Логическая связки: «тогда и
только тогда», «необходимо и
достаточно», « … равносильно
…».

18.

Основные логические тождества
Идемпотентные законы:
1)
A A A
2)
A A A

19.

Основные логические тождества
Коммутативные законы:
3)
4)
5)
A B B A
A B B A
A B B A

20.

Основные логические тождества
Ассоциативные законы:
6)
A B C A B C
7)
A B C A B C
8)
A B C A B C

21.

Дистрибутивные законы:
9)
10)
A B C AB AC
A BC A B A C

22.

Законы Моргана:
11)
A B A B
12)
A B A B

23.

Закон двойного отрицания:
13)
A A

24.

Закон противоречия:
14)
A A 0
Закон исключенного третьего:
15)
A A 1

25.

Законы поглощения:
A A B A
A ( A B) A

26.

Тождества, содержащие константы:
A 0 A
A 1 1
A 0 0
A 1 A
A 0 A
A 1 1
0 A 1
1 A A
A 0 A
A 1 A

27.

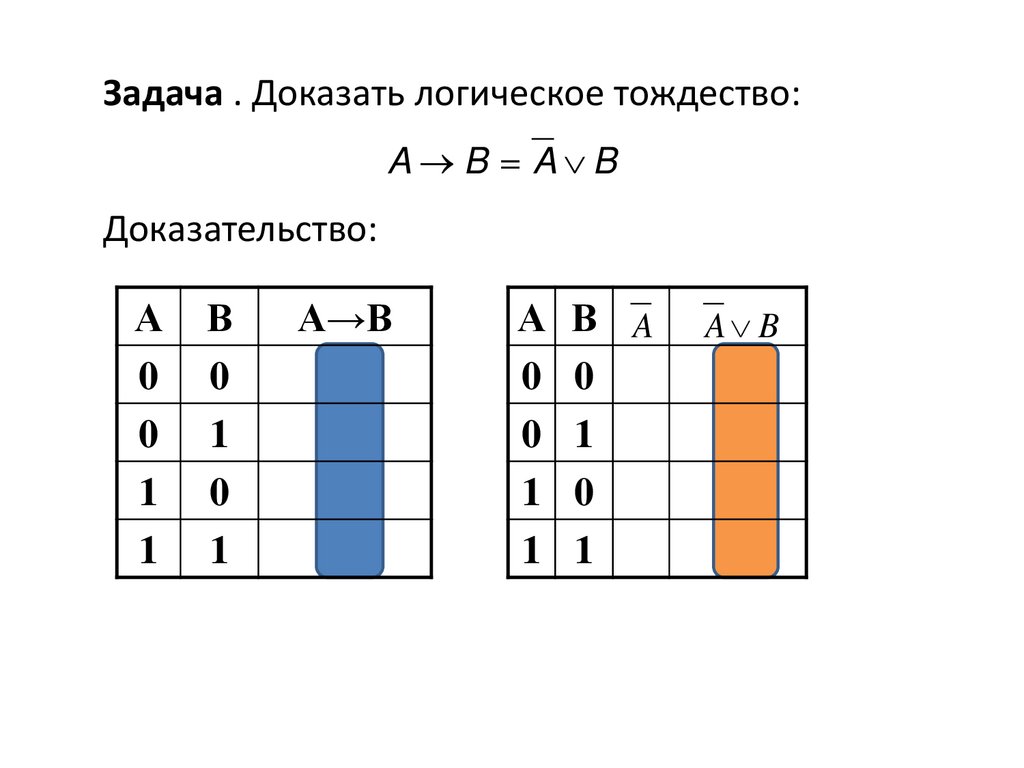
Задача . Доказать логическое тождество:
A B A B
Доказательство:
А
0
0
1
1
В
0
1
0
1
А→В
А В A
0 0
0 1
1 0
1 1
A B

28.

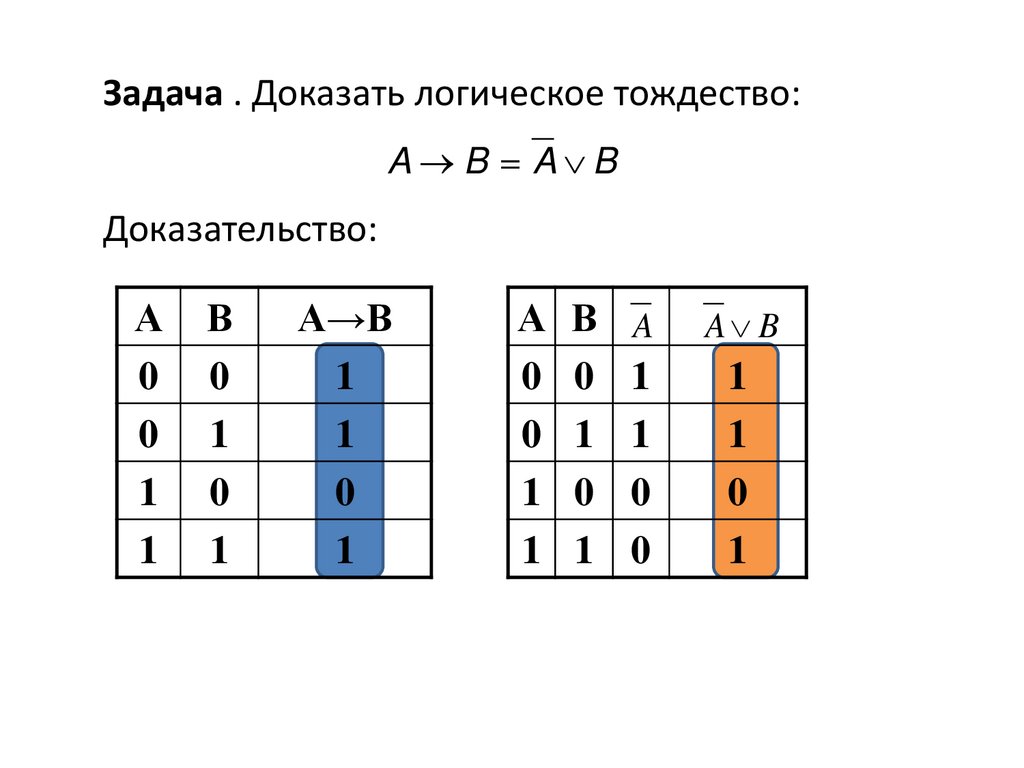
Задача . Доказать логическое тождество:
A B A B
Доказательство:
А
0
0
1
1
В
0
1
0
1
А→В
1
1
0
1
А В
0 0
0 1
1 0
1 1
A
A B
1
1
0
0
1
1
0
1

29.

Определение
Всякое сложное высказывание, которое
может быть получено из простых
высказываний посредством применения
логических
операций
называется
формулой алгебры логики

30.

• Логические значения формулы можно
описать посредством таблицы, содержащей
2n строк, которая называется таблицей
истинности
• n – количество логических переменных
(простых высказываний)в формуле

31.

Виды формул алгебры логики:
• тождественно истинные (тавтология)
• тождественно ложные (противоречие)
• выполнимые

32.

Формула тождественно истинная, если она
принимает значение 1 при любых значениях,
входящих в нее простых высказываний.
Формула тождественно ложная, если…
Формула выполнимая, если…

33.

• Задачу об отнесении формулы к тому или
иному классу формул называют проблемой
разрешимости