Изучение пределов как основа математического анализа

1.

Развитие теории пределов в
математике
Изучение пределов как основа математического анализа.
Андрей Пикуля и Владислав Мазур

2.

Важность теории пределов
Теория пределов играет ключевую роль в математическом
анализе, позволяя формализовать понятия бесконечно
малых и сходящихся ряды.
2

3.

Исторические корни теории
пределов
01
Первые понятия связаны с древнегреческими
математиками, которые исследовали понятие
бесконечности и метод исчерпывания. Эти идеи помогли
основам геометрических доказательств и интегральных
методов.
02
Средневековое развитие основано на трудах арабских и
европейских математиков, которые внесли вклад в анализ
непрерывности и предвосхитили идеи, развиваемые в
эпоху Возрождения.
3

4.

Основные понятия в теории пределов
Предел функции
Определяет поведение функции при приближении
аргумента к определенной точке.
Расходящиеся ряды
Ряды, сумма которых не имеет конечного предела,
увеличиваясь бесконечно.
Сходящиеся ряды
Ряды, сумма которых стремится к определенному
значению при увеличении числа слагаемых.
Эпсилон-дельта определение
Математическое определение, описывающее предел
через малые изменения.
4

5.

Ключевые фигуры в истории
теории пределов
Рене Декарт сыграл важную роль, введя аналитическую
геометрию, что стало основой для последующих исследований
пределов.
Исаак Ньютон и Карл Вейерштрасс способствовали развитию
исчисления и строгих определений, обеспечив основы
современного анализа.
5

6.

Формализация понятий в XIX веке
Карл Вейерштрасс ввел строгое
эпсилон-дельта определение
предела, решив многие парадоксы
и упрощая анализ.
6
Огюстен Луи Коши разрабатывал идеи
сходящихся и расходящихся рядов,
формализируя понятия интегралов и
производных.
Работы Вейерштрасса и Коши
обеспечили необходимую основу
для строгого математического
анализа, которая используется и
по сей день.

7.

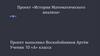
Развитие понимания пределов
На диаграмме показана эволюция концепции
пределов, начиная с античных времён до
современных теорий.Историческое развитие
теории пределов продемонстрировало переход
от интуитивных понятий к строгим
математическим формализациям.
7
Восходящая эволюция математических понятий с акцентом на пределы, 2023.

8.

Методы доказательства в анализе
Применение теории пределов в математическом
анализе позволяет строго формулировать и
доказывать свойства функций. Эти методы
лежат в основе дифференциального и
интегрального исчисления.
8
Анализ с использованием пределов
рассматривает процессы, которые выглядят
бесконечно малыми, обеспечивая точность и
логическую обоснованность выводов.

9.

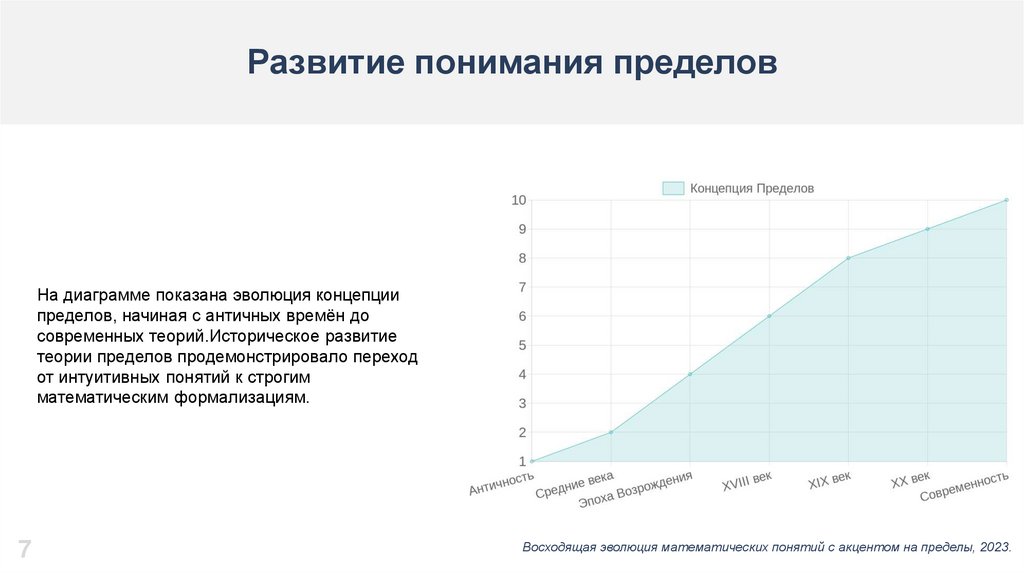
Основные темы теории пределов в высшей
математике
Понятие предела функции
Пределы и непрерывность
Изучение поведения функций при стремлении аргумента к
заданной точке. Основы анализа в математике.
Обсуждение связи пределов с непрерывностью функций и
их применением в решении уравнений.
Сходимость и абсолютная сходимость
Исследование видов сходимости рядов, влияющих на корректность
вычислений и результаты в анализе.
9

10.

Математическое
моделирование и пределы
Теория пределов позволяет моделировать непрерывные
явления, улучшая точность и предсказуемость математических
моделей.
Включает анализ динамических систем и их устойчивости,
расширяя возможности применения в науке и технике.
10

11.

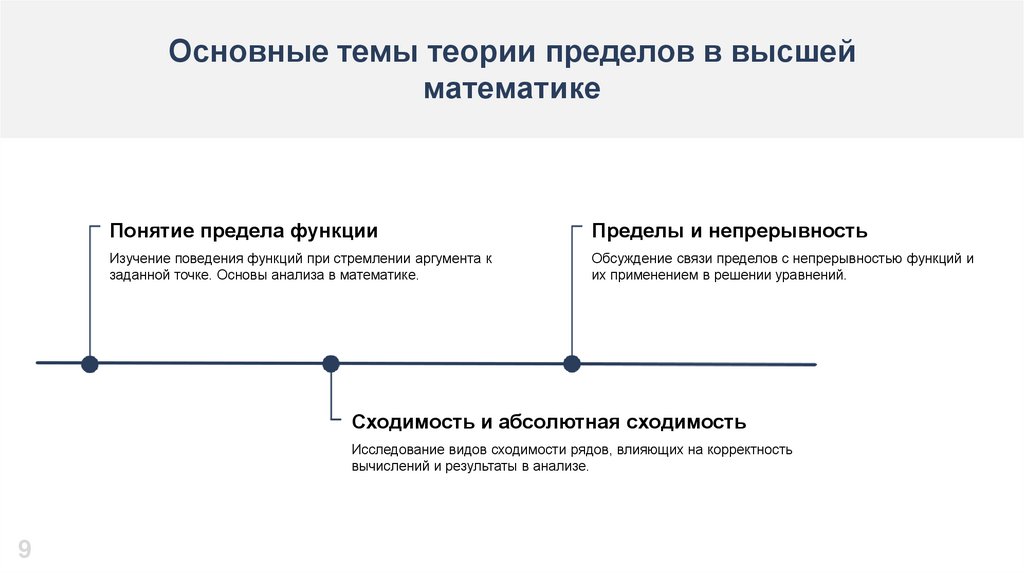
Примеры использования пределов
Экономические модели используют пределы
при анализе финансовых показателей за
длительный период времени.Экономика и
инженерия активно применяют пределы,
подтверждая важность математических
инструментов в анализе.
12
Собранные данные исследований различных статей с 2023 года

12.

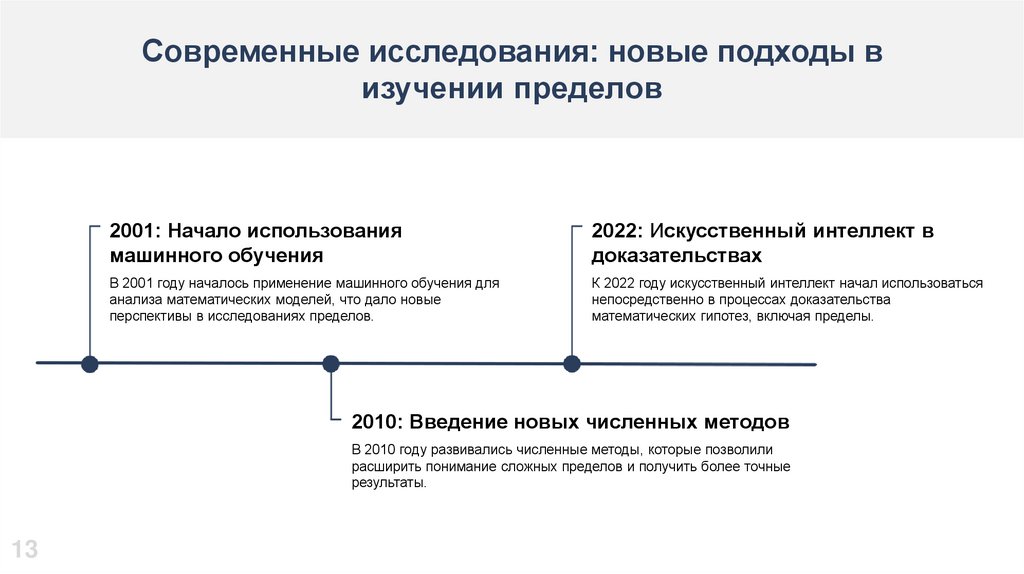
Современные исследования: новые подходы в
изучении пределов
2001: Начало использования
машинного обучения
2022: Искусственный интеллект в
доказательствах
В 2001 году началось применение машинного обучения для
анализа математических моделей, что дало новые
перспективы в исследованиях пределов.
К 2022 году искусственный интеллект начал использоваться
непосредственно в процессах доказательства
математических гипотез, включая пределы.
2010: Введение новых численных методов
В 2010 году развивались численные методы, которые позволили
расширить понимание сложных пределов и получить более точные
результаты.
13

13.

Теория пределов и
вычислительная математика:
практика и инновации
Приложения в вычислениях
Использование пределов в вычислительной математике
позволяет решать сложные задачи моделирования реальных
процессов. Они помогают ускорить расчёты и повысить их
точность.
Инновации и разработки
Современные разработки включают использование новых
алгоритмов и программ, что улучшает возможности
вычислительных моделей. Это способствует научным прорывам
в различных отраслях.
14

14.

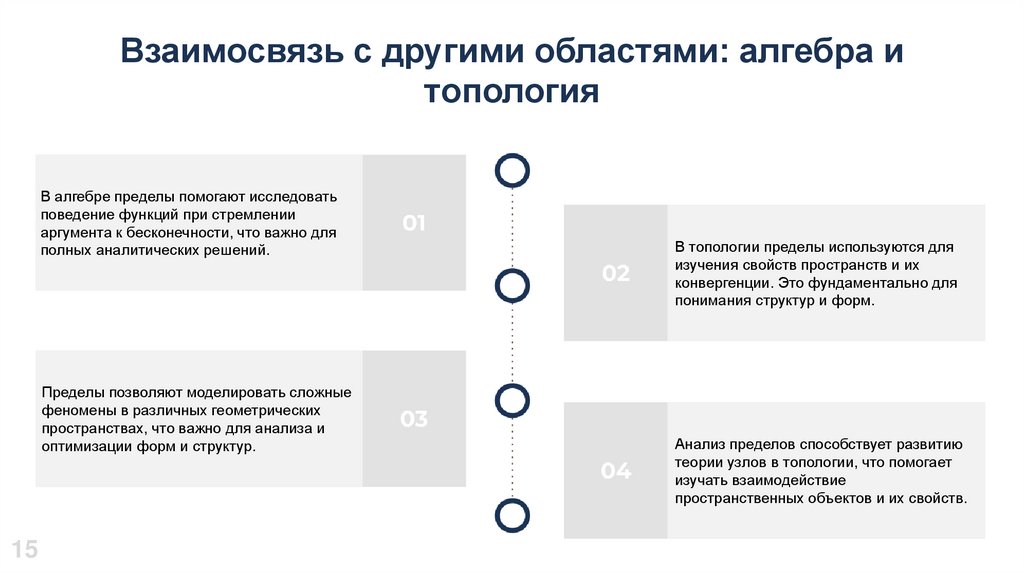
Взаимосвязь с другими областями: алгебра и
топология
В алгебре пределы помогают исследовать
поведение функций при стремлении
аргумента к бесконечности, что важно для
полных аналитических решений.
Пределы позволяют моделировать сложные
феномены в различных геометрических
пространствах, что важно для анализа и
оптимизации форм и структур.
15
В топологии пределы используются для
изучения свойств пространств и их
конвергенции. Это фундаментально для
понимания структур и форм.
Анализ пределов способствует развитию
теории узлов в топологии, что помогает
изучать взаимодействие
пространственных объектов и их свойств.

15.

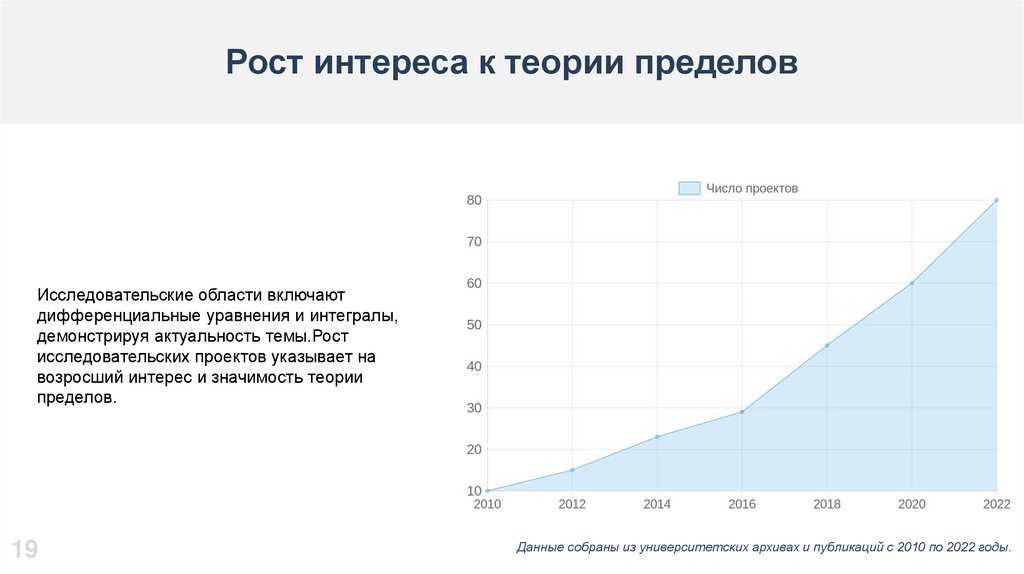
Рост интереса к теории пределов
Исследовательские области включают
дифференциальные уравнения и интегралы,
демонстрируя актуальность темы.Рост
исследовательских проектов указывает на
возросший интерес и значимость теории
пределов.
19
Данные собраны из университетских архивах и публикаций с 2010 по 2022 годы.

16.

Заключение: Значимость теории
пределов
Теория пределов играет ключевую роль в математике и её приложениях. Она
открывает новые пути для исследований и инноваций в научных и прикладных
областях.

17.

Спасибо за внимание!!!