Свойства 2-х, 3-х степенных и лазерных гироскопов. Датчики угловых скоростей

1.

Лекция № 1
Раздел 1. Гироскопические приборы и системы
Тема 1.1. Свойства 2-х,3-х степенных и лазерных
гироскопов. Датчики угловых скоростей
Цели, задачи и порядок изучения дисциплины
1. Основные свойства и конструкция 3-х
степенного гироскопа
2. Примеры определения вектора прецессии
3. Понятие гироскопического момента
4. Карданов подвес
5. Теорема Резаля
6. Уравнения движения трехстепенного гироскопа.
7. Свойство прецессии

2.

Цели и задачи изучения дисциплины
38
Цели освоения дисциплины
Дать студентам необходимые знания для формирования
профессиональных знаний и практических навыков по вопросам
теории, принципам действия, конструкции и особенностям
эксплуатации информационно – измерительных систем воздушных
судов.
Место дисциплины в структуре ООП бакалавриата
Дисциплина относится к вариативной части профессионального
цикла федерального государственного образовательного стандарта по
специальности 25.03.02 «Техническая эксплуатация авиационных
электросистем и пилотажно-навигационных комплексов».
Курс базируется на знаниях студентов, полученных при изучении
дисциплин Высшая математика, Автоматика и управление, Основы
аэродинамики, Электрорадиоизмерения, Бортовые цифровые
вычислительные устройства, Авиационные приборы.

3.

37
Цели и задачи изучения дисциплины
Компетенции, формируемые в процессе изучения
дисциплины, необходимы для освоения в дальнейшем дисциплин
эксплуатационной направленности: ПНК, АЭС и ПНК конкретного
вида ВС, Техническое обслуживание и ремонт авиационных
электросистем и пилотажно-навигационных комплексов,
Государственный экзамен и формирует знания, умения и
компетенции, необходимые для изучения этих дисциплин.
Дисциплина изучается в 6-м семестре на лекциях (34
часа), практических занятиях (32 часа) и лабораторных работах
(52 часа). По дисциплине предусмотрен: 6 семестр - экзамен.
На самостоятельное изучение дисциплины отводится
66 часов.
На промежуточную аттестацию – 32 часа

4.

36
Основная литература
1. В. Г. Воробьёв, В.В. Глухов, И.К. Кадышев. Авиационные
приборы, информационно- измерительные системы и комплексы. М.:
Транспорт 1992.
Дополнительная литература
1. В.Г. Воробьёв, В. П. Зыль, С.В. Кузнецов Комплексы
цифрового пилотажно- навигационного оборудования. Часть 1.
Учебное пособие М.:МГТУГА,1998.140 с.
2. В.М. Попов. Авиационные информационно-измерительные
системы. Пособие к лабораторным работам по разделу
«Гироскопические приборы и системы». Часть 1. Иркутск: ИФ МГТУ
ГА, 2016
3. В.М. Попов. Авиационные информационно-измерительные
системы. Пособие к лабораторным работам по разделу
«Гироскопические приборы и системы». Часть 2. Иркутск: ИФ МГТУ
ГА, 2016
4. В.М. Попов, Диль В.Ф. Авиационные информационноизмерительные системы. Пособие к лабораторным работам по
разделу «Инерциальные системы навигации. Средства отображения
информации».Часть 3. Иркутск: ИФ МГТУ ГА, 2020

5.

35
Порядок изучения дисциплины
Дисциплина состоит из трех разделов.
В разделе 1 - Гироскопические приборы и системы
рассматриваются вопросы использования гироскопа для измерения
углов пространственной ориентации ВС тангажа и крена в
гировертикалях и авиагоризонтах, углов поворота ВС в указателях
поворота, угловых скоростей вращения ВС относительно
строительных осей в датчиках угловых скоростей, в курсовых
системах для измерения различных курсов ВС, принцип построения
лазерных гироскопов .
В разделе 2 - Навигационные системы ВС ГА
рассматриваются вопросы определения координат ВС с
использованием навигационных вычислителей, инерциальных
систем навигации, определение углов пространственной ориентации,
курса и координат ВС с помощью инерциальной курсовертикали.
В разделе 3 – Средства отображения информации
рассматриваются вопросы отображения информации на приборных
панелях с помощью электромеханических и электронных средств.

6.

1. Основные свойства и конструкция
3-х степенного гироскопа
Гироскопом называется быстровращающееся
симметричное твердое тело (ротор) с одной неподвижной
точкой. Оно устанавливается в специальном подвесе
(называемом кардановым), который обеспечивает ротору две или
три вращательные степени свободы относительно основания
Ротор и внутренняя рамка образуют так называемый гироузел.
В авиационных гироскопах гироузел представляет собой
асинхронный электрический двигатель,
у которого угловая
скорость вращения ротора может достигать от 24 000 до
120 000 об/мин.
Одной из основных характеристик гироскопа
является
вектор кинетического момента ротора H , направление
которого совпадает с направлением вектора угловой скорости
вращения ротора
34

7.

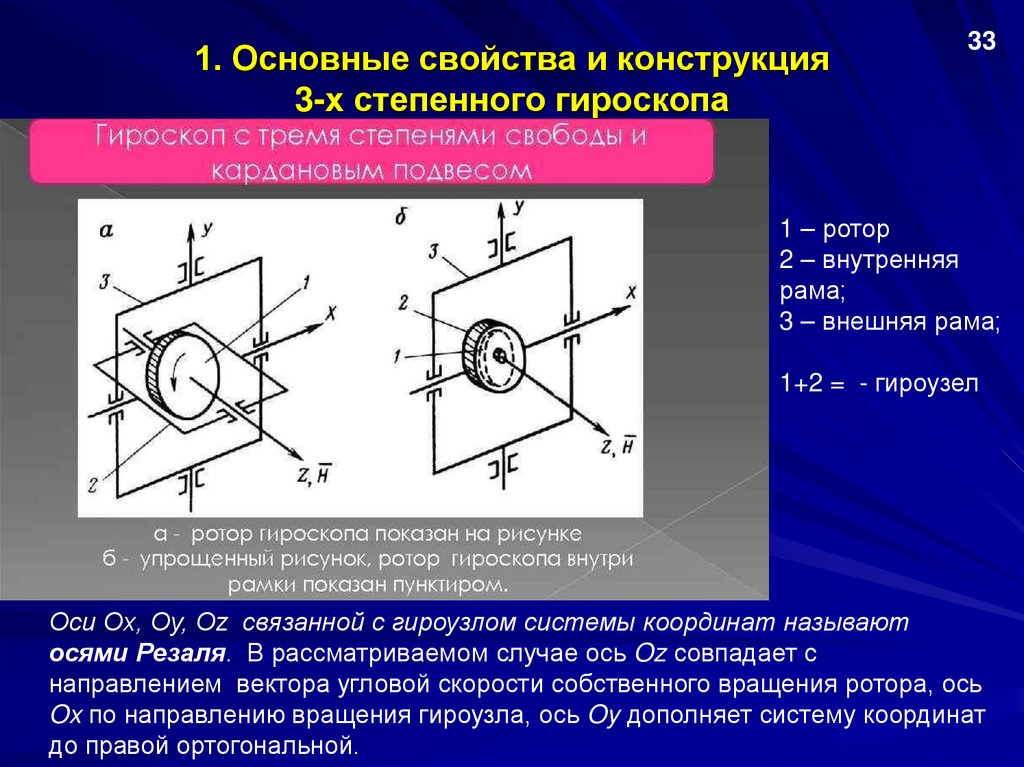
1. Основные свойства и конструкция
3-х степенного гироскопа
33
1 – ротор
2 – внутренняя
рама;
3 – внешняя рама;
1+2 = - гироузел
Оси Ox, Oy, Oz связанной с гироузлом системы координат называют
осями Резаля. В рассматриваемом случае ось Oz совпадает с
направлением вектора угловой скорости собственного вращения ротора, ось
Ox по направлению вращения гироузла, ось Oy дополняет систему координат
до правой ортогональной.

8.

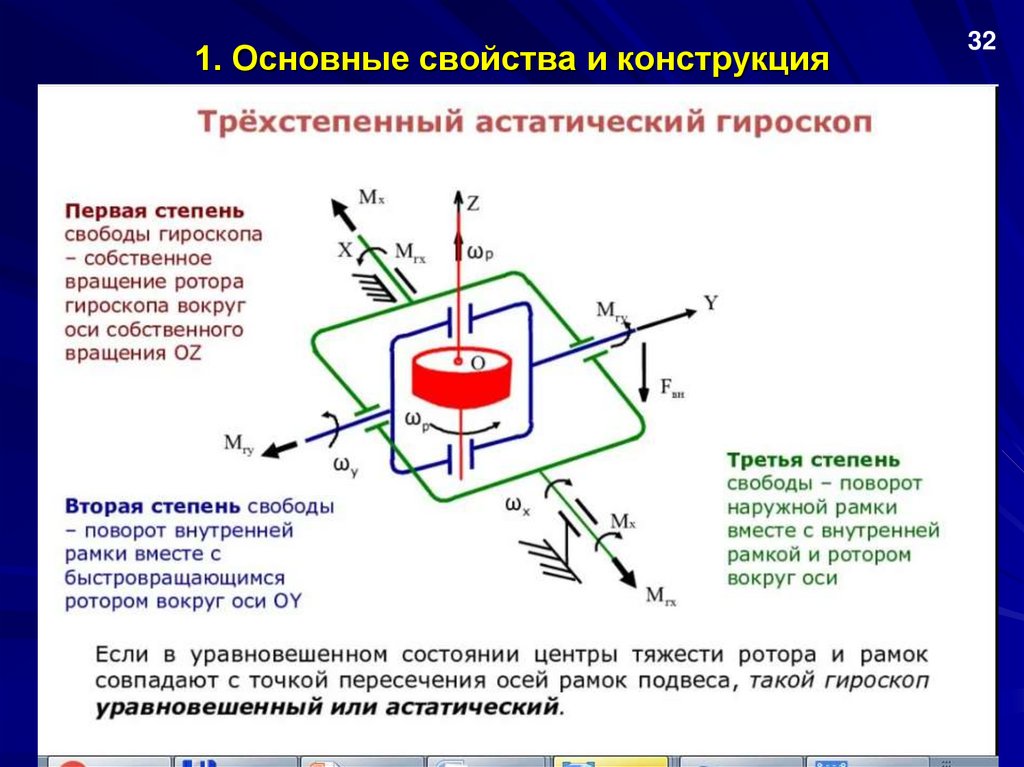
1. Основные свойства и конструкция
3-х степенного гироскопа
32

9.

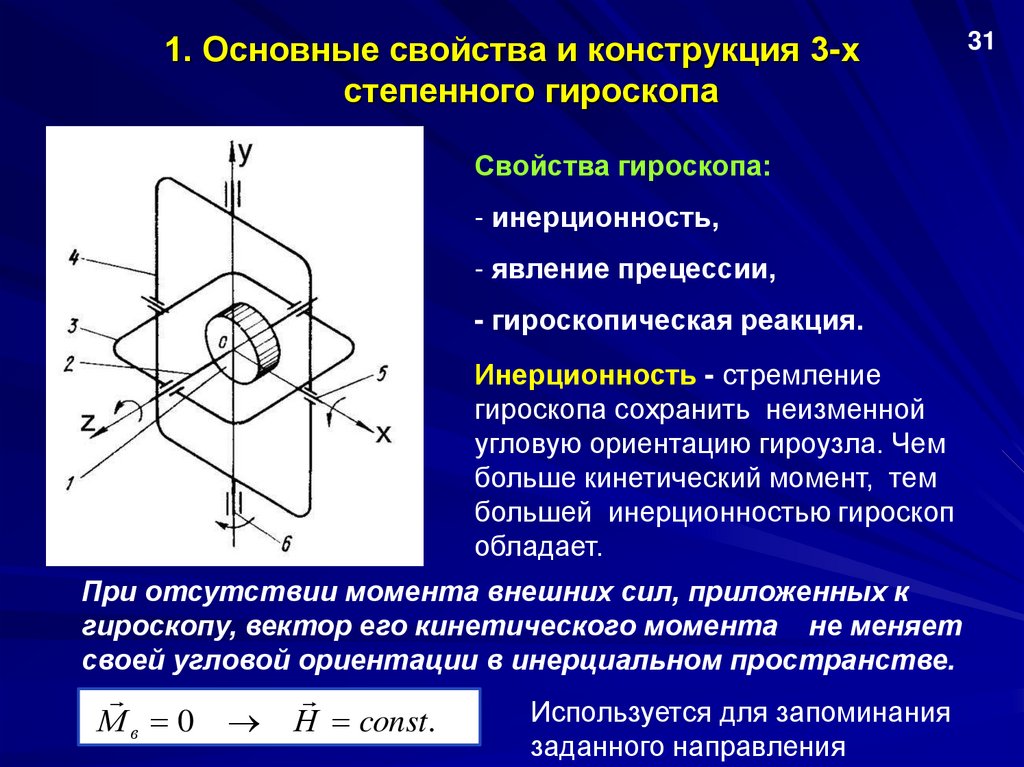
1. Основные свойства и конструкция 3-х
степенного гироскопа
Свойства гироскопа:
- инерционность,
- явление прецессии,
- гироскопическая реакция.
Инерционность - стремление
гироскопа сохранить неизменной
угловую ориентацию гироузла. Чем
больше кинетический момент, тем
большей инерционностью гироскоп
обладает.
При отсутствии момента внешних сил, приложенных к
гироскопу, вектор его кинетического момента не меняет
своей угловой ориентации в инерциальном пространстве.
Мв 0
Н const .
Используется для запоминания
заданного направления
31

10.

1. Основные свойства и конструкция 3-х
степенного гироскопа
30
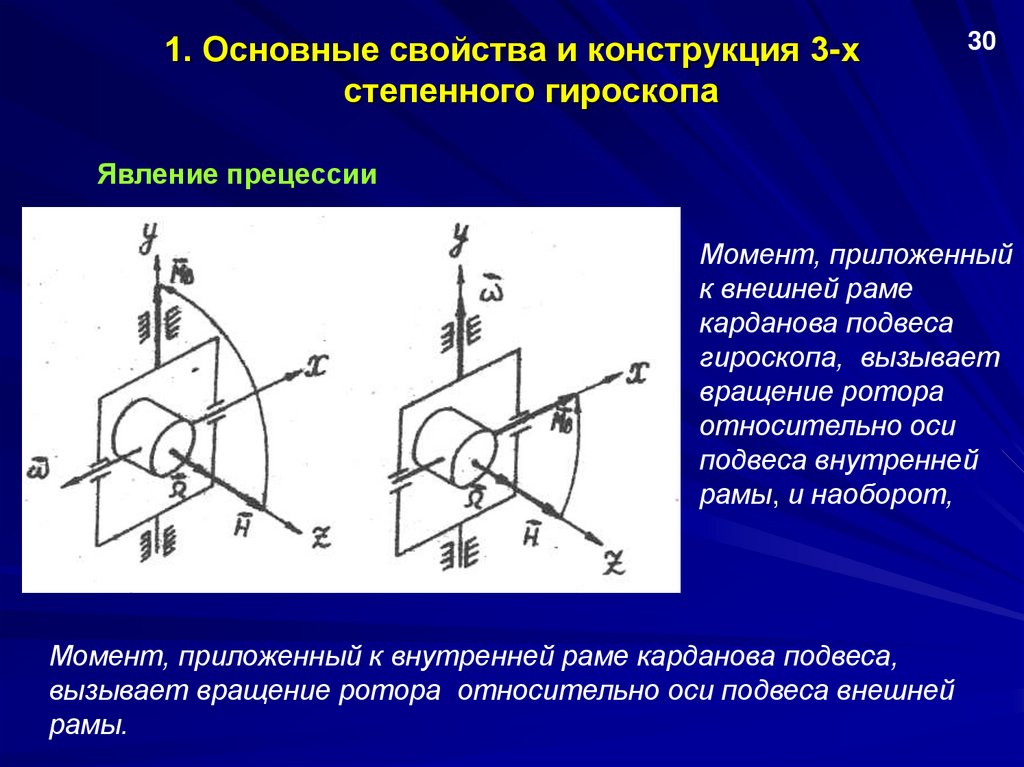
Явление прецессии
Момент, приложенный
к внешней раме
карданова подвеса
гироскопа, вызывает
вращение ротора
относительно оси
подвеса внутренней
рамы, и наоборот,
Момент, приложенный к внутренней раме карданова подвеса,
вызывает вращение ротора относительно оси подвеса внешней
рамы.

11.

1. Основные свойства и конструкция 3-х
степенного гироскопа
Гироскопическая реакция
Гироскопическая реакция заключается в повышенной
сопротивляемости быстровращающегося массивного тела
(ротора) попыткам изменить его положение в пространстве (по
сравнению с его сопротивляемостью при неподвижном роторе).
По своей физической природе гироскопический момент
является главным моментом кориолисовых сил инерции,
возникающих при одновременном наличии двух угловых движений:
- относительного (вокруг оси собственного вращения с угловой
скоростью );
- переносного (вокруг осей карданова подвеса гироузла с угловой
скоростью
Для определения направления гироскопического момента
пользуются правилом Н.Е.Жуковского.
29

12.

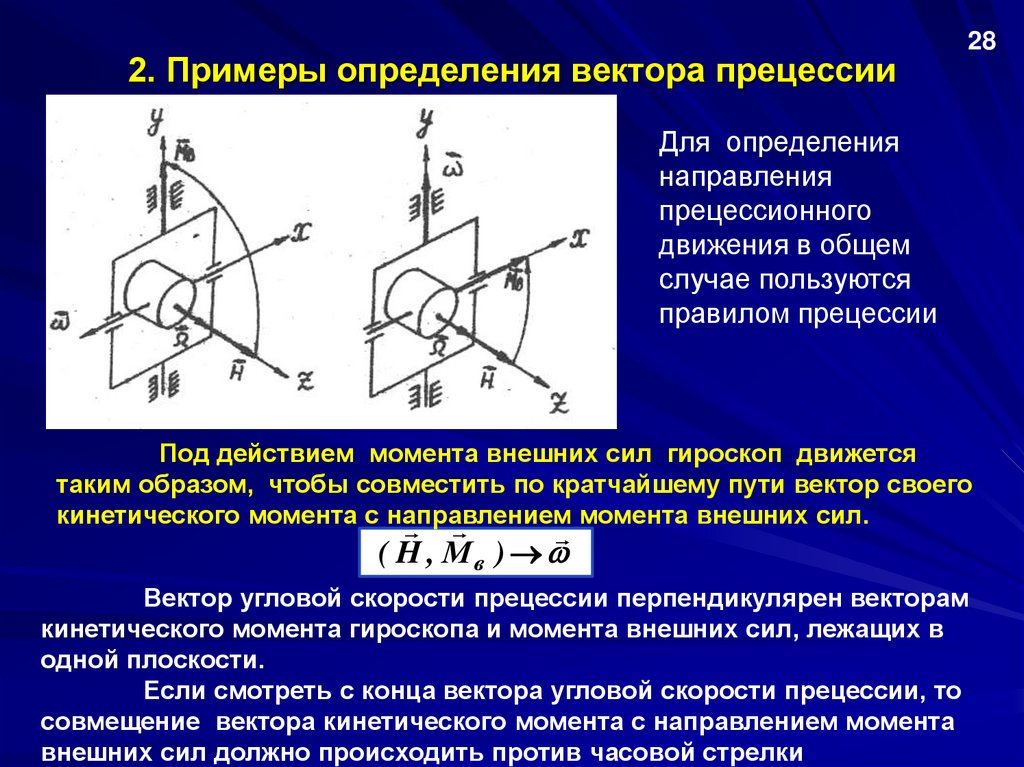
2. Примеры определения вектора прецессии
28
Для определения
направления
прецессионного
движения в общем
случае пользуются
правилом прецессии
Под действием момента внешних сил гироскоп движется
таким образом, чтобы совместить по кратчайшему пути вектор своего
кинетического момента с направлением
момента внешних сил.
( H , Мв )
Вектор угловой скорости прецессии перпендикулярен векторам
кинетического момента гироскопа и момента внешних сил, лежащих в
одной плоскости.
Если смотреть с конца вектора угловой скорости прецессии, то
совмещение вектора кинетического момента с направлением момента
внешних сил должно происходить против часовой стрелки

13.

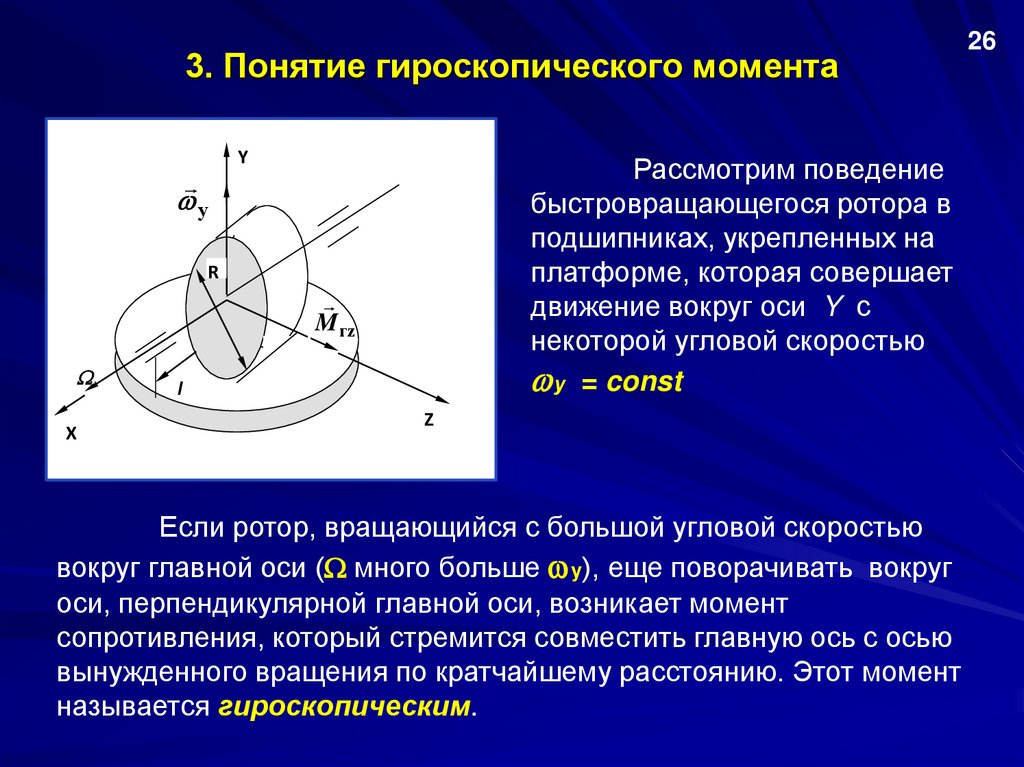
3. Понятие гироскопического момента
Y
Рассмотрим поведение
быстровращающегося ротора в
подшипниках, укрепленных на
платформе, которая совершает
движение вокруг оси Y с
некоторой угловой скоростью
у = const
y
R
M гz
X
l
Z
Если ротор, вращающийся с большой угловой скоростью
вокруг главной оси ( много больше y), еще поворачивать вокруг
оси, перпендикулярной главной оси, возникает момент
сопротивления, который стремится совместить главную ось с осью
вынужденного вращения по кратчайшему расстоянию. Этот момент
называется гироскопическим.
26

14.

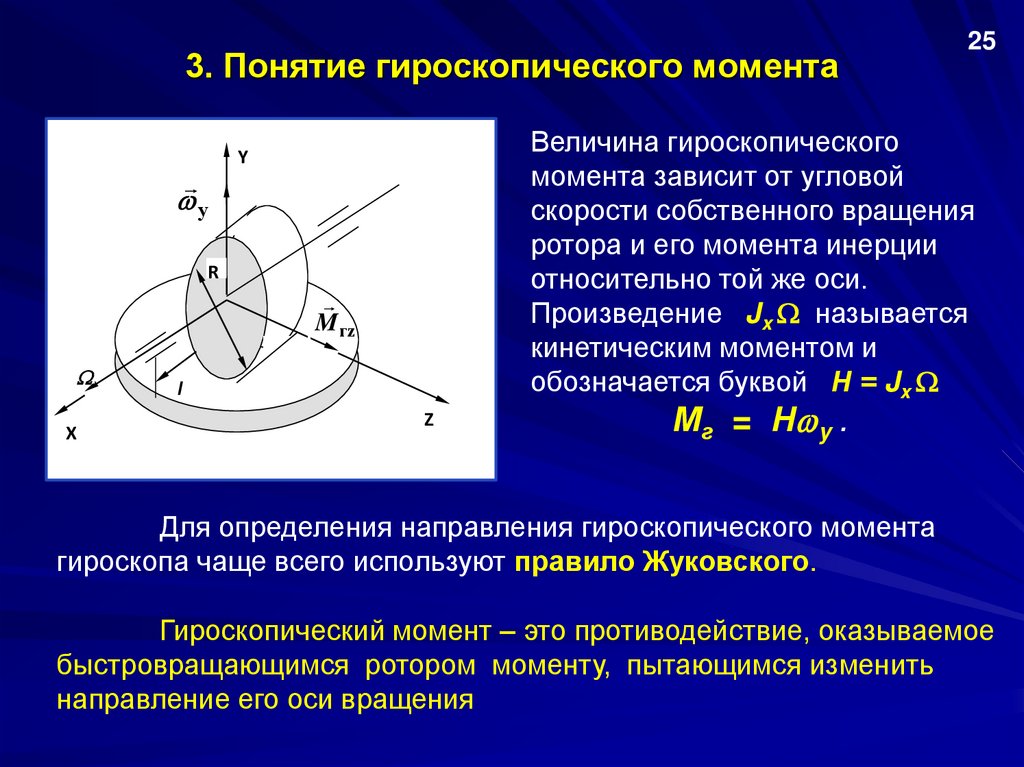
3. Понятие гироскопического момента
Величина гироскопического
момента зависит от угловой
скорости собственного вращения
ротора и его момента инерции
относительно той же оси.
Произведение Jx называется
кинетическим моментом и
обозначается буквой Н = Jx
Y
y
R
M гz
X
25
l
Z
Мг = Н y .
Для определения направления гироскопического момента
гироскопа чаще всего используют правило Жуковского.
Гироскопический момент – это противодействие, оказываемое
быстровращающимся ротором моменту, пытающимся изменить
направление его оси вращения

15.

3. Понятие гироскопического момента
24
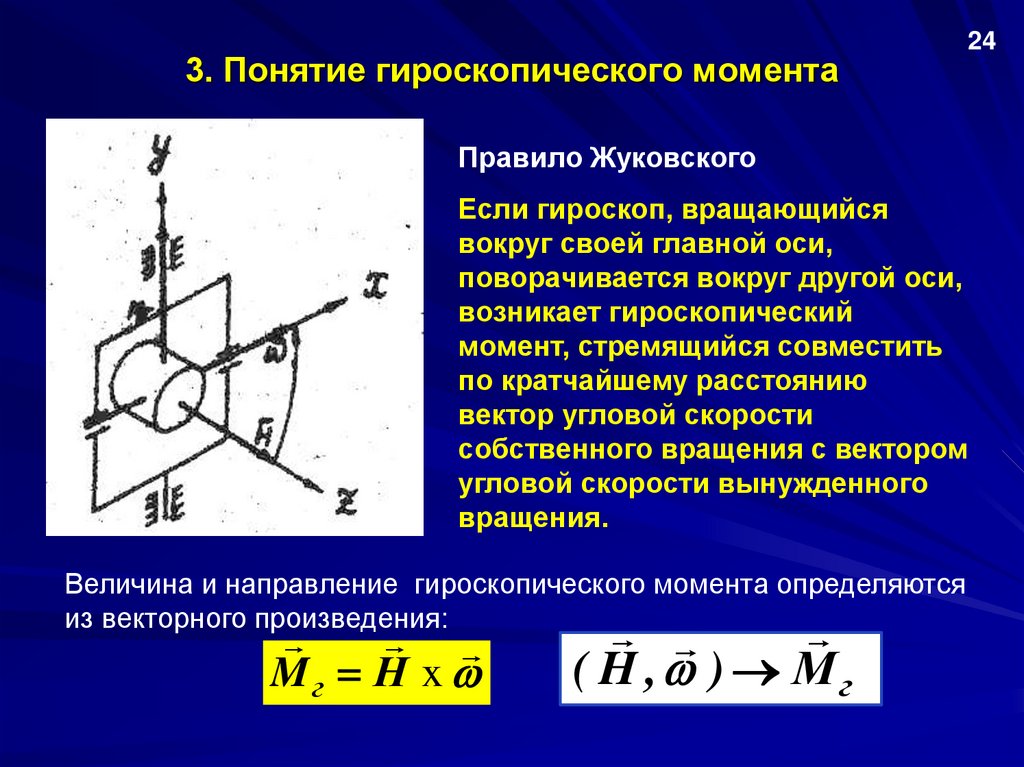
Правило Жуковского
Если гироскоп, вращающийся
вокруг своей главной оси,
поворачивается вокруг другой оси,
возникает гироскопический
момент, стремящийся совместить
по кратчайшему расстоянию
вектор угловой скорости
собственного вращения с вектором
угловой скорости вынужденного
вращения.
Величина и направление гироскопического момента определяются
из векторного произведения:
Mг Н x
( H , ) Мг

16.

4. Карданов подвес
23
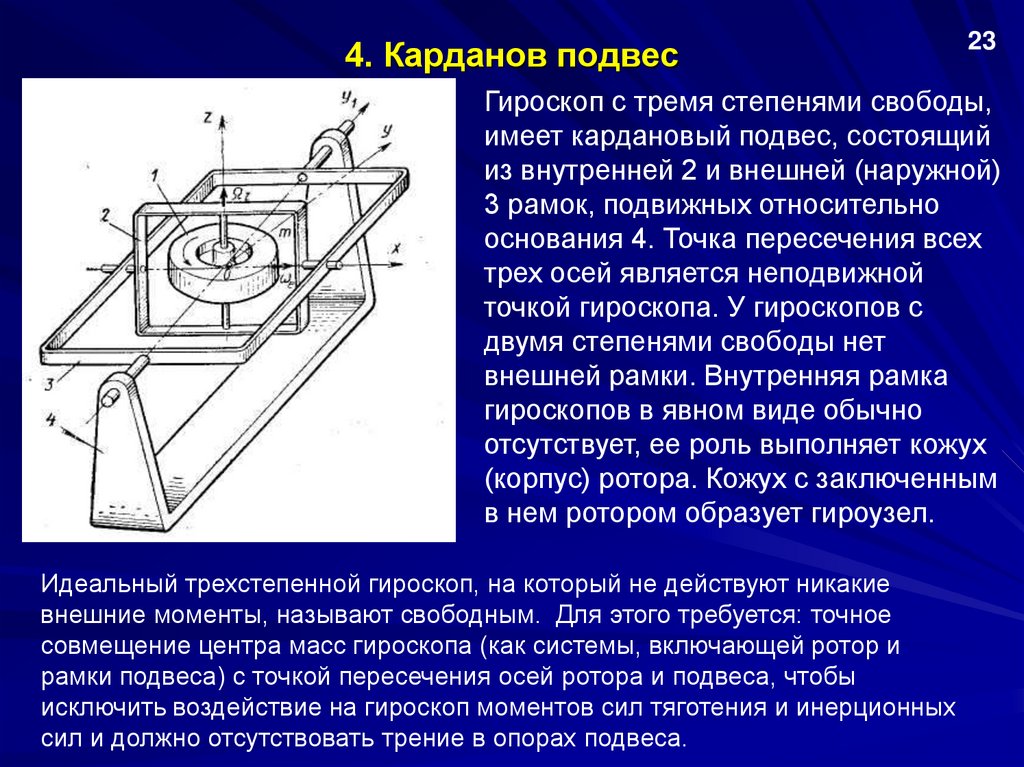
Гироскоп с тремя степенями свободы,
имеет кардановый подвес, состоящий
из внутренней 2 и внешней (наружной)
3 рамок, подвижных относительно
основания 4. Точка пересечения всех
трех осей является неподвижной
точкой гироскопа. У гироскопов с
двумя степенями свободы нет
внешней рамки. Внутренняя рамка
гироскопов в явном виде обычно
отсутствует, ее роль выполняет кожух
(корпус) ротора. Кожух с заключенным
в нем ротором образует гироузел.
Идеальный трехстепенной гироскоп, на который не действуют никакие
внешние моменты, называют свободным. Для этого требуется: точное
совмещение центра масс гироскопа (как системы, включающей ротор и
рамки подвеса) с точкой пересечения осей ротора и подвеса, чтобы
исключить воздействие на гироскоп моментов сил тяготения и инерционных
сил и должно отсутствовать трение в опорах подвеса.

17.

4. Карданов подвес
1
2 11
y
3
4
6
x
5
12
z
8
10
9
22
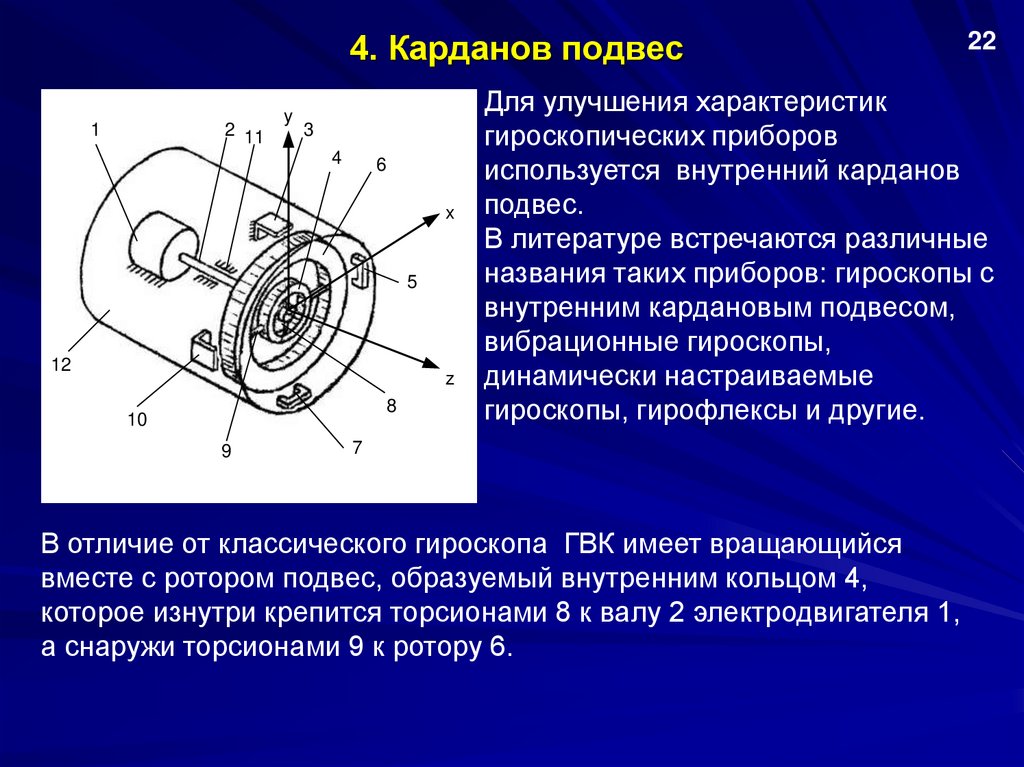
Для улучшения характеристик
гироскопических приборов
используется внутренний карданов
подвес.
В литературе встречаются различные
названия таких приборов: гироскопы с
внутренним кардановым подвесом,
вибрационные гироскопы,
динамически настраиваемые
гироскопы, гирофлексы и другие.
7
В отличие от классического гироскопа ГВК имеет вращающийся
вместе с ротором подвес, образуемый внутренним кольцом 4,
которое изнутри крепится торсионами 8 к валу 2 электродвигателя 1,
а снаружи торсионами 9 к ротору 6.

18.

4. Карданов подвес
1
2 11
y
3
4
6
x
5
12
z
8
10
9
7
21
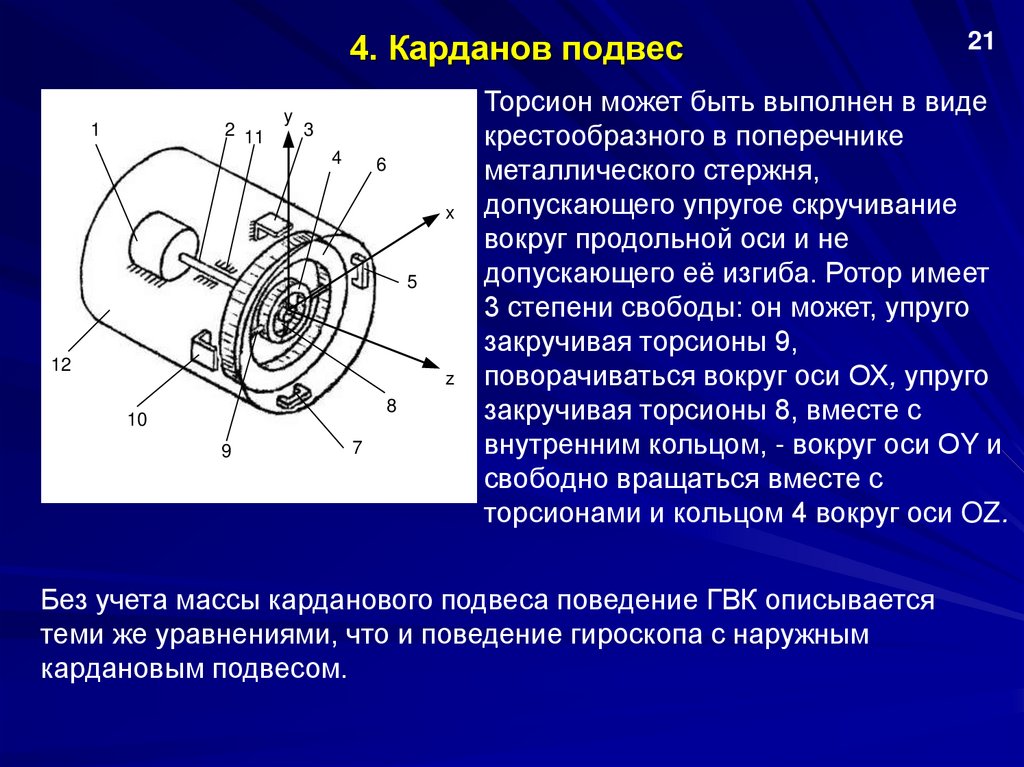
Торсион может быть выполнен в виде
крестообразного в поперечнике
металлического стержня,
допускающего упругое скручивание
вокруг продольной оси и не
допускающего её изгиба. Ротор имеет
3 степени свободы: он может, упруго
закручивая торсионы 9,
поворачиваться вокруг оси ОХ, упруго
закручивая торсионы 8, вместе с
внутренним кольцом, - вокруг оси ОY и
свободно вращаться вместе с
торсионами и кольцом 4 вокруг оси OZ.
Без учета массы карданового подвеса поведение ГВК описывается
теми же уравнениями, что и поведение гироскопа с наружным
кардановым подвесом.

19.

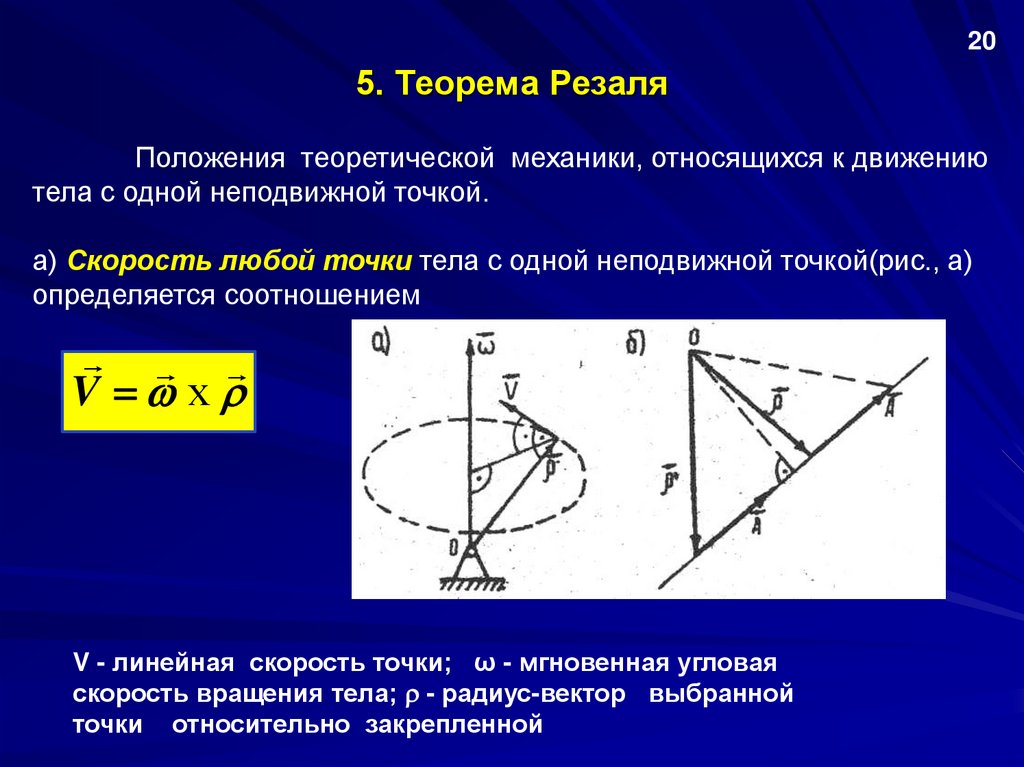
20
5. Теорема Резаля
Положения теоретической механики, относящихся к движению
тела с одной неподвижной точкой.
а) Скорость любой точки тела с одной неподвижной точкой(рис., а)
определяется соотношением
V х
V - линейная скорость точки; ω - мгновенная угловая
скорость вращения тела; - радиус-вектор выбранной
точки относительно закрепленной

20.

19
5. Теорема Резаля
б ) Количеством движения материальной точки называется
вектор
K mV
m - масса точки; V - ее скорость.
в) Моментом количества движения материальной точки m
относительно точки O будет вектор
G х mV
Моментом количества движения системы материальных точек
с массами mi называется вектор
G i x miVi
i
Производная от вектора G по времени для случая системы
материальных точек
(e )
(i )
(e )
(e)
G xm V xm V xF xF x F M
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i

21.

18
5. Теорема Резаля
(e )
(i )
(e )
(e)
G i xm i Vi i xm i Vi i xFi i xFi i xFi M
i
i
(i )
i xmi Vi 0 i xFi 0
i
i
i
i
i
Суммарный момент всех
внутренних сил равен нулю
i
Суммарный момент внешних сил
(e )
G M
i
Теорема о моменте количества движения (теорема Резаля)
абсолютная скорость конца вектора момента количества
движения системы материальных точек равняется моменту
внешних сил, воздействующих на эту систему

22.

17
5. Теорема Резаля
Если движение конца вектора G,рассматривается в некоторой системе
координат xyz, вращающейся со скоростью ω, то абсолютная
скорость конца этого вектора складывается из относительной и
переносной скорости
d~
(e)
G G(t ) x G M
dt
(1)
Cпроектируем векторы, стоящие в левой и правой частях
уравнения (1), на оси координат системы xyz ( оси Резаля),
~
dG y
dGz
dG x
d
G( t ) i
j
z
dt
dt
dt
dt
i
x G x
Gx
j
y
Gy
относительная
скорость
k
z i( yG z zG y ) j( xG z zG x ) k ( xG y yG x )
Gz

23.

16
5. Теорема Резаля
dG x
yG z z G y M x
dt
dG y
yG z zG y M y
dt
dGz
xG y yG x M z
dt
(2)
Динамические
Уравнения Эйлера
Момент количества движения G тела с одной неподвижной
точкой, вращающегося с угловой скоростью ω
Gx = Jxx x - Jxy y - Jxz z ,
Gy = - Jyx x + Jyy y - Jyz z ,
Gz = - Jzx x - Jzy y + Jzz z ,
Jxx , Jxy - осевые и центробежные
моменты инерции
Оси xyz - главные оси инерции,
центробежные моменты инерции
равны 0
Gx = Jxx x,
Gy = Jyy y ,
Gz = Jzz z.
(3)

24.

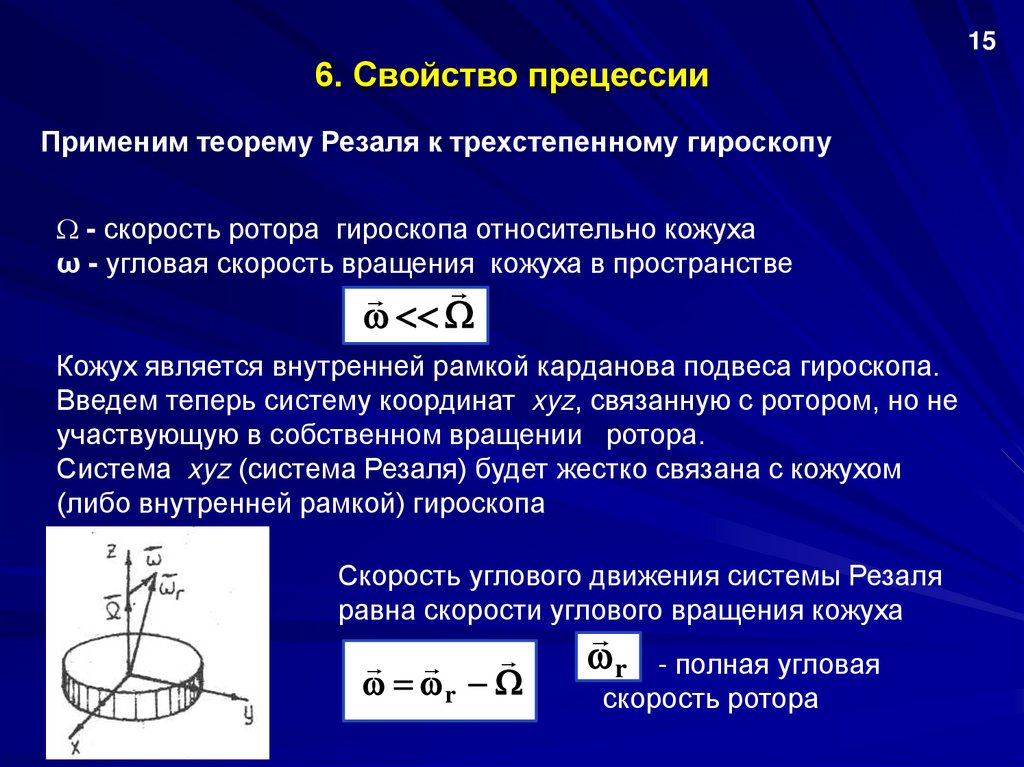
15
6. Свойство прецессии
Применим теорему Резаля к трехстепенному гироскопу
- скорость ротора гироскопа относительно кожуха
ω - угловая скорость вращения кожуха в пространстве
Кожух является внутренней рамкой карданова подвеса гироскопа.
Введем теперь систему координат xyz, связанную с ротором, но не
участвующую в собственном вращении ротора.
Система xyz (система Резаля) будет жестко связана с кожухом
(либо внутренней рамкой) гироскопа
Скорость углового движения системы Резаля
равна скорости углового вращения кожуха
r
r
- полная угловая
скорость ротора

25.

14
6. Свойство прецессии
Найдем момент количества движения
r
G
ротора (3)
Gx = Jxx x, Gy = Jyy y , Gz = Jzz z.
r
G = Jэ i rx + Jэ j ry + Jп k rz ,
(4)
i, j, k - орты осей xyz; Jп = Jzz – полярный момент инерции ротора;
Jэ = Jxx = Jyy - экваториальный момент инерции ротора.
rx x ry y rz z
- проекции полной
угловой скорости ротора
x , y , z - проекции вектора на оси xyz
r
G = Jэ i x + Jэ j y + Jп k( z + ),
r
Так как x , y , z<< , то G Jп k = kH
H = Jп -кинетический момент гироскопа , является
постоянным вектором и по величине и по направлению

26.

13
6. Свойство прецессии
Таким образом, производная от вектора H относительно системы
координат xyz будет равна 0:
~
dH
0
dt
Найдем угловую скорость движения гироскопа (кожуха - внутренней
рамки гироскопа), обусловленную приложенным моментом к
ротору.
По теореме о кинетическом моменте имеем
~ r
dG
r
xG M
dt
~
r
d
H
Так как G Н , а
0 , то x Н M
(5)
dt
(5) - уравнение прецессии, а движение, которое оно описывает,
называют прецессией гироскопа

27.

12
6. Свойство прецессии
Запишем аналитические уравнения, соответствующие выражению (5)
x
x
0
y
y
0
z
M x
z M y .
M z
H
y H M x ,
x H M y .
аналитическая запись
прецессионного
движения гироскопа в
проекциях на оси
Резаля
Так как векторы Н, М и ω образуют правую ортогональную тройку –
векторное произведение , то отсюда вытекает известное правило
прецессии:
под действием внешнего момента гироскоп движется
таким образом, чтобы совместить по кратчайшему пути
ось своего вращения с направлением внешнего момента.
Иногда закон прецессии (5) записывают в форме
Mг x Н (6)
М - Мг = 0
называют гироскопическим моментом, который по своей природе
является моментом кориолисовых сил инерции.

28.

7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
11
xН M
При выводе уравнения прецессии (5)
были сделаны некоторые упрощающие допущения:
r
G Н
Выведем полные и линеаризованные уравнения движения гироскопа,
сравним их с уравнением прецессии и определим, с какой степенью
точности уравнение прецессии описывает движение гироскопа.
Положение ротора гироскопа в кардановом
подвесе задается тремя углами Эйлера,
являющимися углами поворотов рамок и
ротора относительно друг друга. Любое
положение гироскопа может быть получено
тремя последовательными поворотами на
углы , и относительно некоторого
исходного фиксированного положения.

29.

7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
10
Поворачивая гироскоп относительно оси АВ - на угол , относительно
оси DE - на угол , и относительно оси собственного вращения - на
угол , перейдем от исходного положения - оси
к заданному
x,y,z - жестко связана с кожухом .
Если основание П гироскопа либо, точнее
говоря, выбранная начальная система
отсчета
поворачивается в
пространстве с угловой скоростью
п i пx j пy k пz
то с учетом угловых скоростей ротора
относительно основания, задаваемых
величинами
, и
получаем проекции угловой скорости
ротора rx , ry , rz

30.

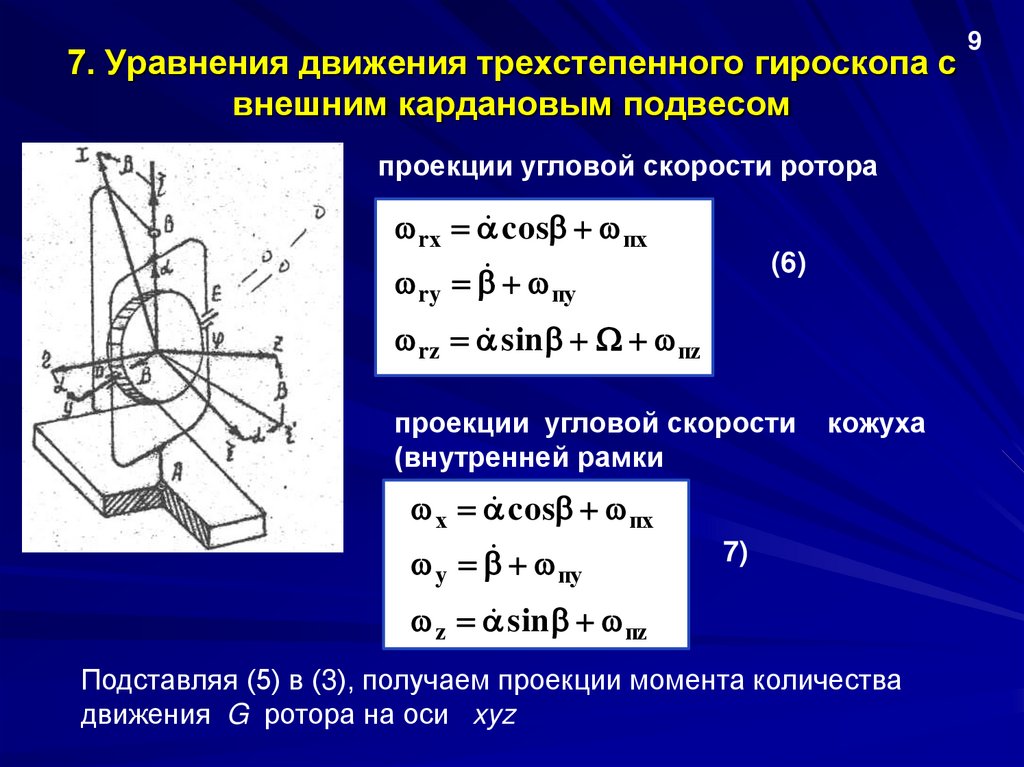
7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
проекции угловой скорости ротора
rх cos пх
ry
(6)
пy
rz sin пz
проекции угловой скорости
(внутренней рамки
х cos пх
y
пy
кожуха
7)
z sin пz
Подставляя (5) в (3), получаем проекции момента количества
движения G ротора на оси xyz
9

31.

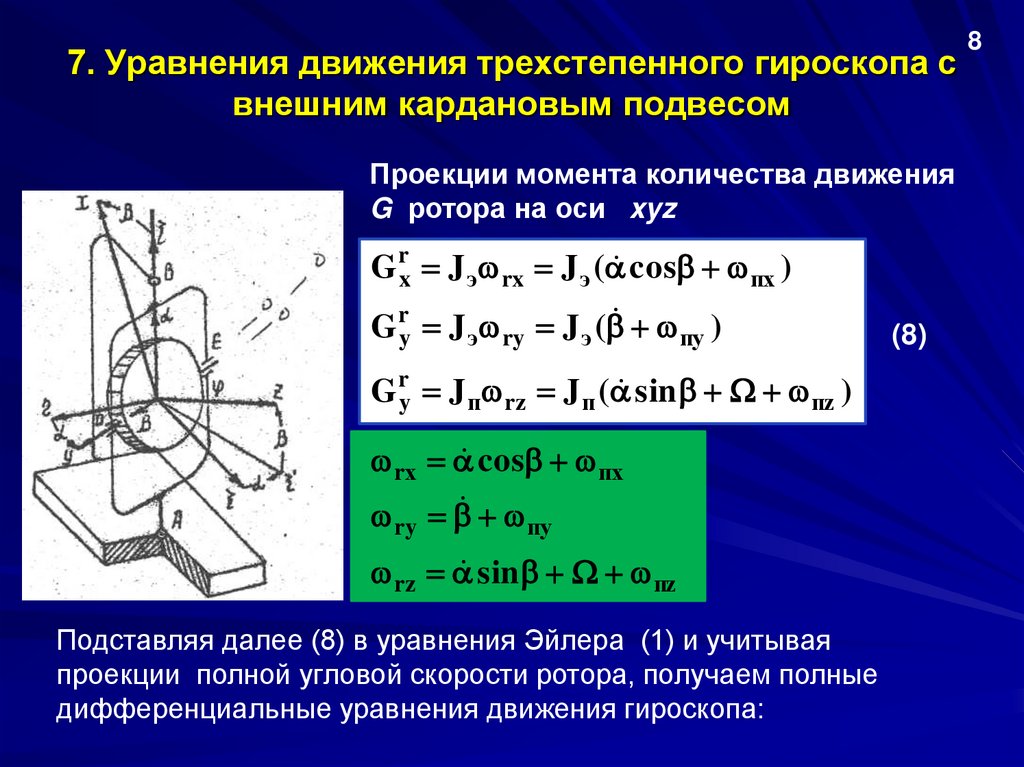
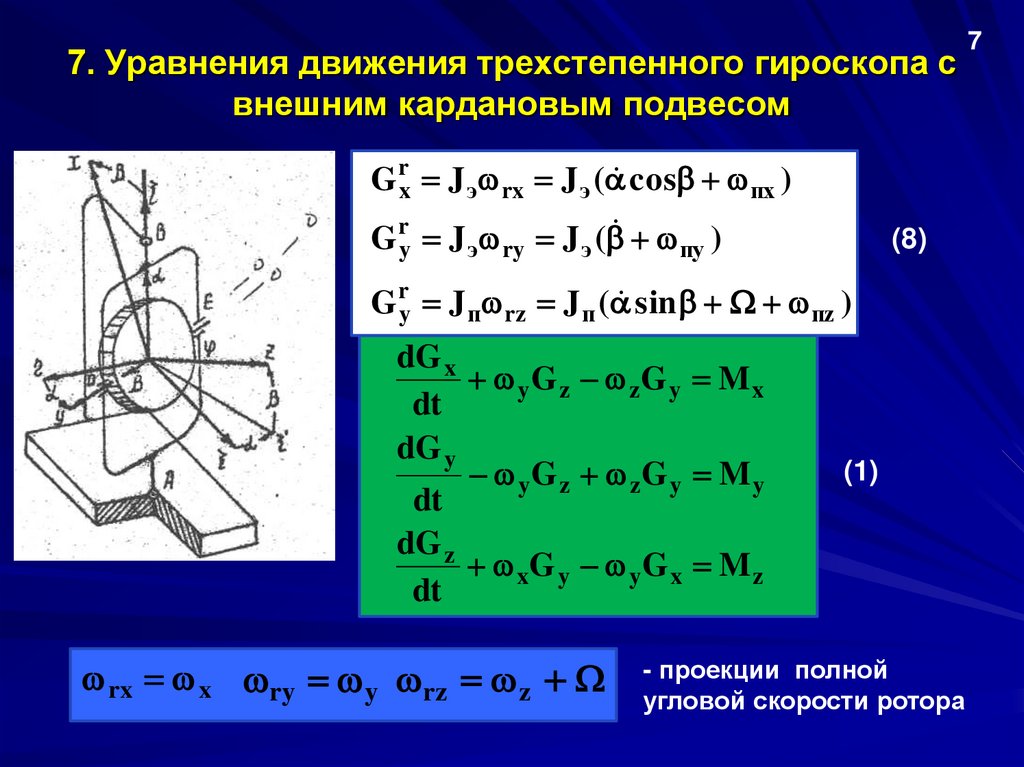
7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
Проекции момента количества движения
G ротора на оси xyz
G rx J э rx J э ( cos пх )
G ry J э ry J э ( пy )
G ry J п rz J п ( sin пz )
rх cos пх
ry
пy
rz sin пz
Подставляя далее (8) в уравнения Эйлера (1) и учитывая
проекции полной угловой скорости ротора, получаем полные
дифференциальные уравнения движения гироскопа:
(8)
8

32.

7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
G rx J э rx J э ( cos пх )
G ry J э ry J э ( пy )
(8)
G ry J п rz J п ( sin пz )
dG x
y G z z G y M x
dt
dG y
y G z z G y M y
dt
dG z
xG y y G x M z
dt
rx x ry y rz z
(1)
- проекции полной
угловой скорости ротора
7

33.

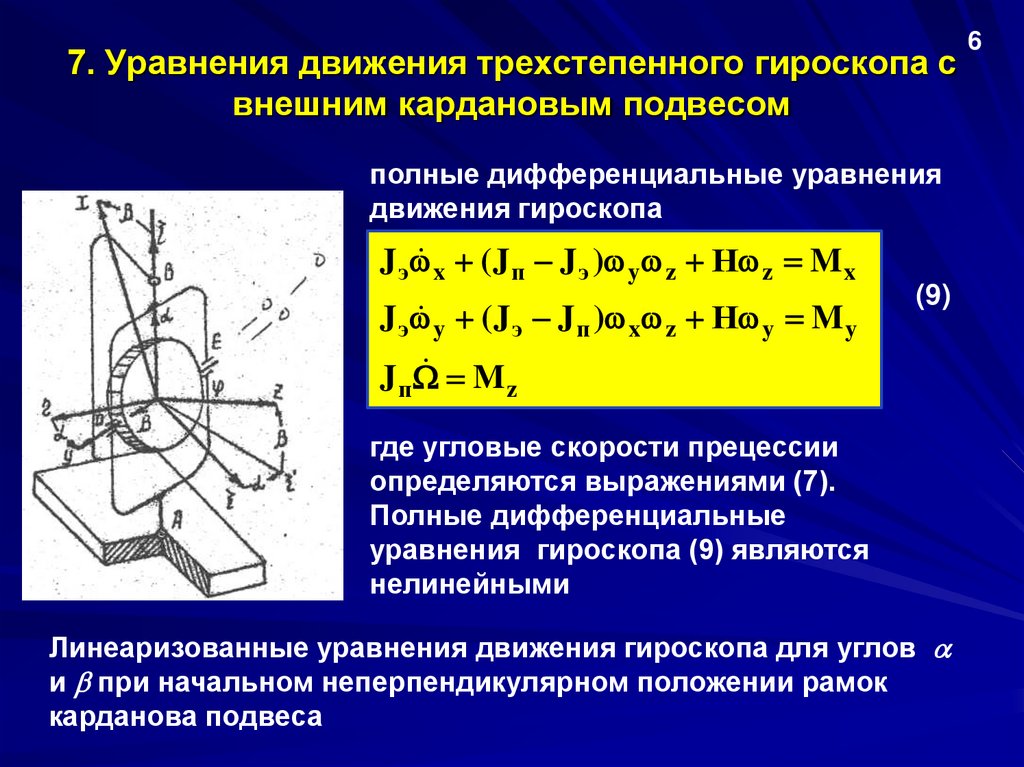
7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
полные дифференциальные уравнения
движения гироскопа
x ( J п J э ) y z Н z M x
J э
y ( J э J п ) x z Н y M y
J э
(9)
Mz
J п
где угловые скорости прецессии
определяются выражениями (7).
Полные дифференциальные
уравнения гироскопа (9) являются
нелинейными
Линеаризованные уравнения движения гироскопа для углов
и при начальном неперпендикулярном положении рамок
карданова подвеса
6

34.

7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
5
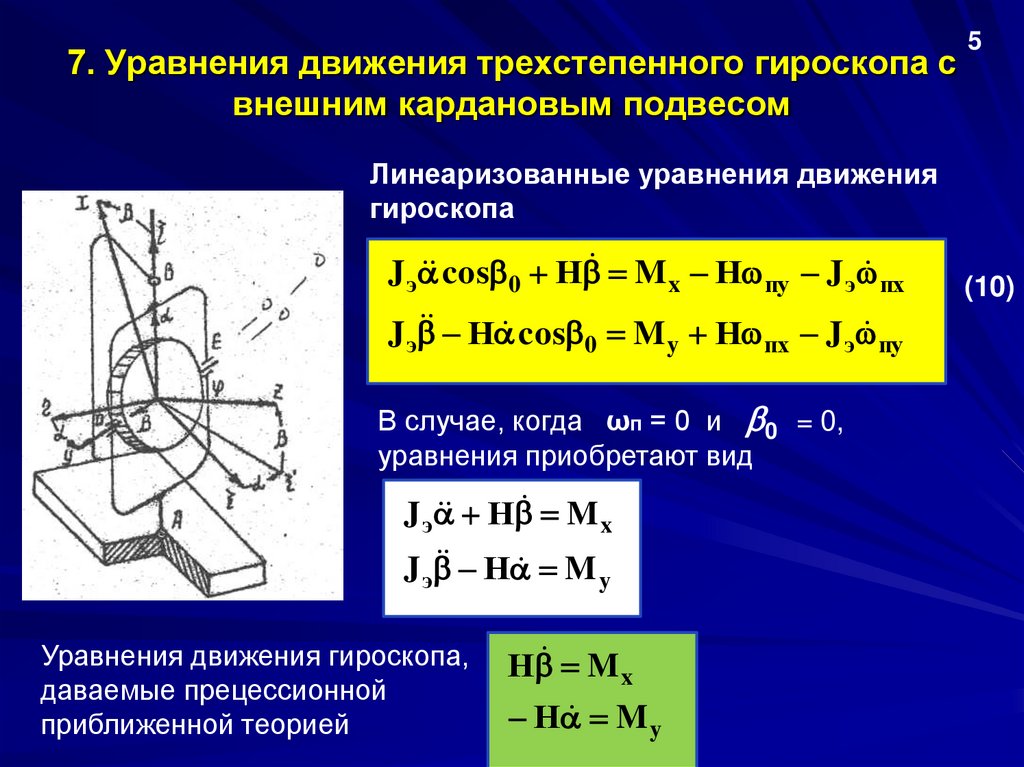
Линеаризованные уравнения движения
гироскопа
cos 0 Н M x Н пy J э
пx
J э
Н cos M Н J
J э
0
y
пx
э пy
В случае, когда ωп = 0 и 0 = 0,
уравнения приобретают вид
Н M x
J э
Н M
J
э
Уравнения движения гироскопа,
даваемые прецессионной
приближенной теорией
y
Н M x
Н M y
(10)

35.

7. Уравнения движения трехстепенного гироскопа с
внешним кардановым подвесом
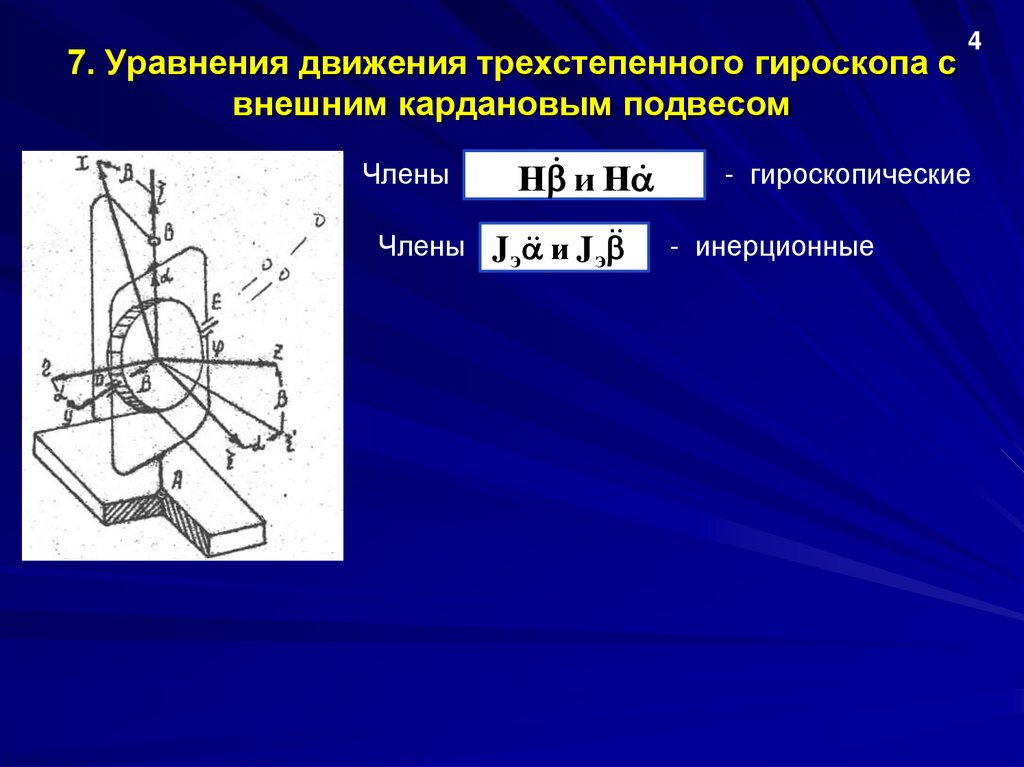
Члены
Н и Н
Члены J э
и J э
4
- гироскопические
- инерционные

36.

8. Нутация
3
Нутацией называется колебательное движение оси ротора
гироскопа, накладывающееся на ее основное прецессионное
движение. Кроме того, нутацией называют движение гироскопа по
инерции. Нутация возникает вместе с прецессией и продолжает
существовать после прекращения прецессии. Прецессия
прекращается сразу же, как только на гироскоп перестает
действовать внешний момент. Нутацию можно рассматривать как
переходный процесс, происходящий в гироскопе.
Приложим относительно оси ОУ
мгновенный момент или импульс силы
(удар), который заставит гироскоп
прецессировать вокруг оси ОХ с угловой
скоростью пр1, которая будет нарастать от
нуля. При этом вследствие инерции ротора
и внутренней рамки карданова подвеса
появится реактивный момент L2,
действующий в направлении,
противоположном направлению прецессии.
Момент вызовет прецессию относительно
оси ОУ с нарастающей скоростью пр2.

37.

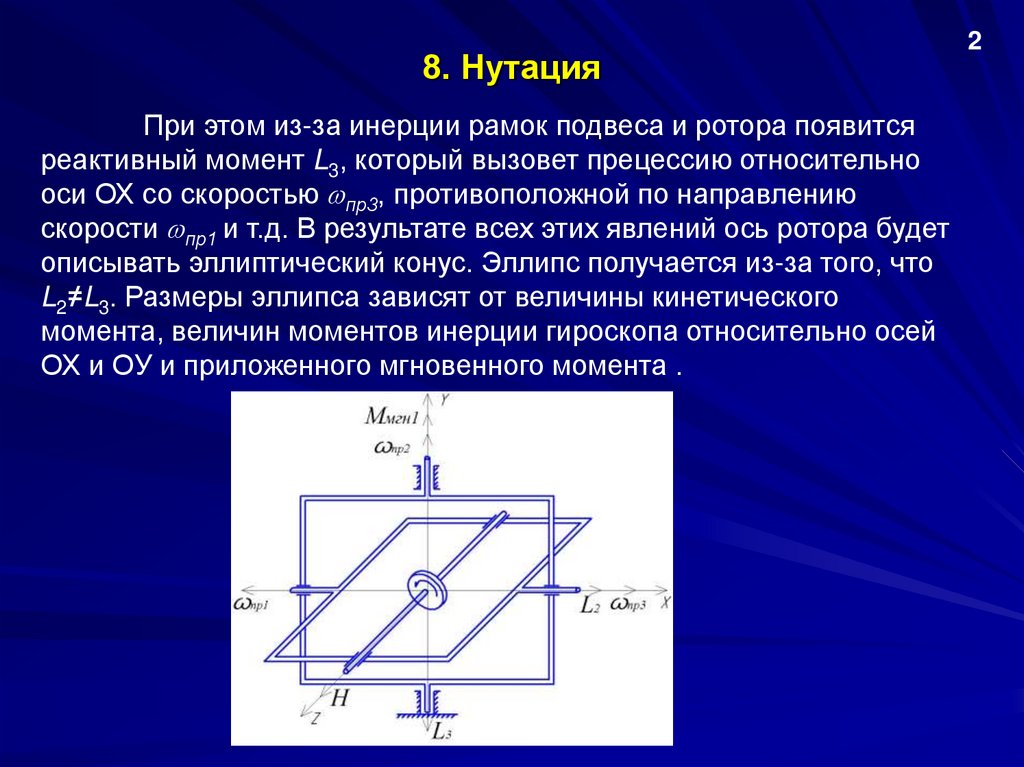
8. Нутация
При этом из-за инерции рамок подвеса и ротора появится
реактивный момент L3, который вызовет прецессию относительно
оси ОХ со скоростью пр3, противоположной по направлению
скорости пр1 и т.д. В результате всех этих явлений ось ротора будет
описывать эллиптический конус. Эллипс получается из-за того, что
L2≠L3. Размеры эллипса зависят от величины кинетического
момента, величин моментов инерции гироскопа относительно осей
ОХ и ОУ и приложенного мгновенного момента .
2

38.

8. Нутация
Возникающие при запуске нутационные колебания оси ротора
имеют значительную амплитуду и небольшую частоту. По мере
увеличения скорости вращения ротора кинетический момент
растет, что приводит к уменьшению амплитуды и увеличению
частоты нутационных колебаний.
2