Расчет управлений потребных для реализации оптимальной траектории захода на посадку самолета при отказе силовой установки

1.

Краснодарское высшее военное авиационное училище летчиков
Для служебного пользования
г. Краснодар
2025 г.

2.

АКТУАЛЬНОСТЬ
2
ДСП
Внедрение разработанной подпрограммы в систему позволит
добиться существенного повышения безопасности полетов.
Интеллектуальная поддержка заключается в выдаче летчику
необходимых рекомендаций по применению авиационных средств
поражения, при групповых действиях, преодолении системы ПВО
противника, а также при выполнении этапов полета (взлет, посадка,
наведение при отказе отдельных элементов комплекса)

3.

МЕТОДОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
3
ДСП
Цель:
повышение безопасности полетов при отказе силовой установки на
этапе выработки решений и управлений при заходе на посадку
Объект:
летательный аппарат
Предмет:
параметры движения летательного аппарата
Задача:
1.Разработка
подпрограммы
для
реализации
специальных
требований по оснащению современных авиационных комплексов
интеллектуальной поддержкой летчика.
2.Формирование и развитие у курсантов умений и навыков по
применению знаний в решении прикладных задач

4.

ЧАСТНЫЕ ЗАДАЧИ
4
ДСП
1.Провести анализ требований при разработке рекомендаций летчику
по действиям при отказе силовой установки
2.Разработать алгоритм захода на посадку летательного аппарата по
функционалу дальности при выполнении ограничений на конце
траектории (скорость планирования на конце траектории равна
посадочной скорости)
3.Разработать
подпрограмму
определения
рациональных
параметров траекторий движения летательного аппарата при отказе
силовой установки

5.

ПОСТАНОВКА ЗАДАЧИ В МАТЕМАТИЧЕСКОМ ВИДЕ
5
ДСП
Расчет аэродинамических характеристик
Поиск рациональной траектории движения
Для решения поставленной задачи необходимо найти векторные
функции u (t ) и x (t ) , доставляющие максимум функционалу:
T
J ( x( ),u( )) f ( x(T ), u (T),T) f 0 ( x(t ), u (t ), t )dt ,
T
t0
удовлетворяющие уравнениям движения: x f ( x, u, t ) ,
f=( f V , f , f , f X 0 , f Y0 , f Z0 )T , u ( , a )T , x (V , , , X 0 , Y 0 , Z0 )T , граничным
условиям x(t0 ) x0 , (T ) , X 0 (T ) , Y0 (T ) , Z 0 (T ) - fix , фазовым ограничениям
на
управление
С уaбал 0 .
min ( x) н.в. ( x) ,
K K max ( кр , кр , пер.кр. , зад.кр. )
при

6.

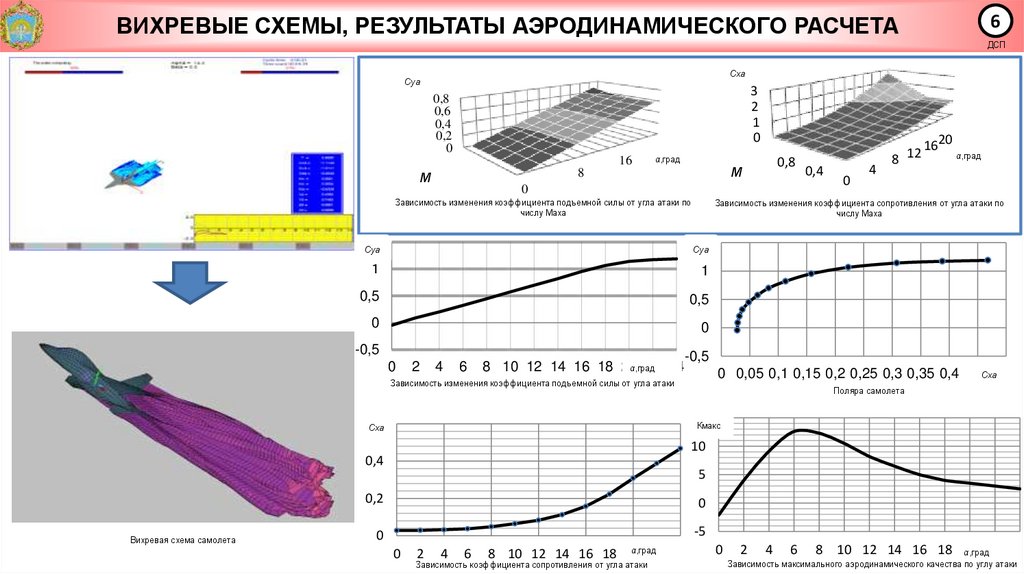
6
ВИХРЕВЫЕ СХЕМЫ, РЕЗУЛЬТАТЫ АЭРОДИНАМИЧЕСКОГО РАСЧЕТА
ДСП
Сха
Суа
3
2
1
0
0,8
0,6
0,4
0,2
0
16
α,град
М
1,5
Суа
1
1
0,5
0,5
0
0
-0,5
4
6
0
4
1620
α,град
Зависимость изменения коэффициента сопротивления от угла атаки по
числу Маха
1,5
Суа
2
0,4
0
Зависимость изменения коэффициента подъемной силы от угла атаки по
числу Маха
0
0,8
М
8
8 12
-0,5
α,град
8 10 12 14 16 18 20
22 24
0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45
Сха0,5
Зависимость изменения коэффициента подъемной силы от угла атаки
Поляра самолета
15
Кмакс
0,6
Сха
10
0,4
5
0,2
Вихревая схема самолета
0
-5
0
0
2
4
6
α,град
α
8 10 12 14 16 18 20 22 24
Зависимость коэффициента сопротивления от угла атаки
0
2
4
6
8
10 12 14 16 18 20 22 24
α,град
Зависимость максимального аэродинамического качества по углу атаки

7.

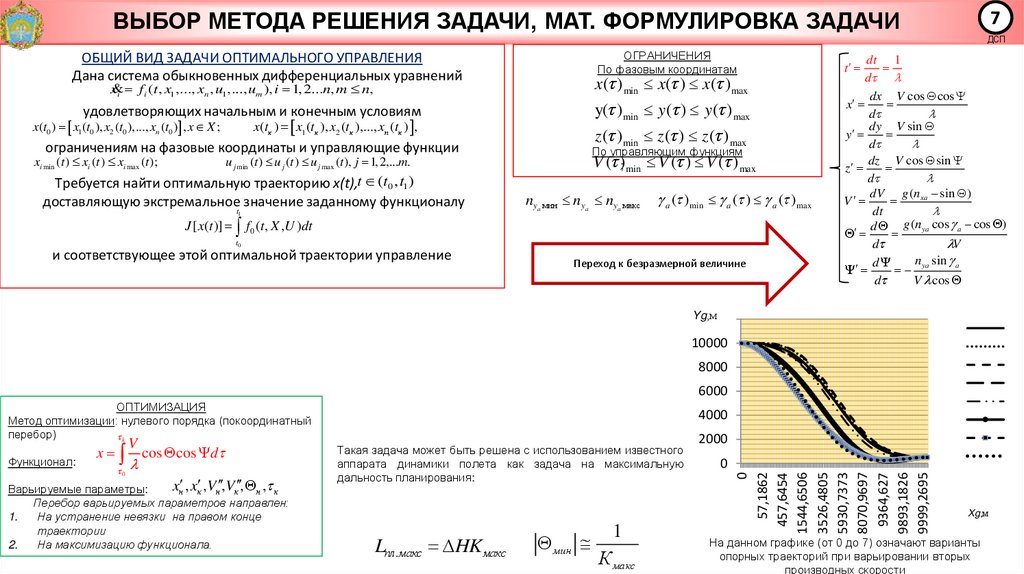
ВЫБОР МЕТОДА РЕШЕНИЯ ЗАДАЧИ, МАТ. ФОРМУЛИРОВКА ЗАДАЧИ
7
ДСП
ОГРАНИЧЕНИЯ
По фазовым координатам
ОБЩИЙ ВИД ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Дана система обыкновенных дифференциальных уравнений
x( ) min x( ) x( ) max
x&
i f i (t , x1 ,..., xn , u1 ,..., u m ), i 1, 2...n, m n,
y( ) min y ( ) y ( ) max
удовлетворяющих начальным и конечным условиям
x(tк ) x1 (tк ), x2 (tк ),..., xn (tк ) ,
x(t0 ) x1 (t0 ), x2 (t0 ),..., xn (t0 ) , x X ;
z ( ) min z ( ) z ( ) max
ограничениям на фазовые координаты и управляющие функции
xi min (t ) xi (t ) xi max (t );
По управляющим функциям
V ( ); min V ( ) V ( ) max
u j min (t ) u j (t ) u j max (t ), j 1,2,...m.
Требуется найти оптимальную траекторию x(t),t (t0 , t1 )
доставляющую экстремальное значение заданному функционалу
t1
nya мин nya nya макс
a ( ) min a ( ) a ( ) max
J [ x(t )] f 0 (t , X ,U )dt
t0
и соответствующее этой оптимальной траектории управление
Переход к безразмерной величине
dt 1
d
dx V cos cos
x
d
dy V sin
y
d
dz V cos sin
z
d
dV g (nxa sin )
V
dt
d g (nya cos a cos )
d
V
nya sin a
d
d
V cos
t
Yg,м
12000
10000
8000
6000
ОПТИМИЗАЦИЯ
Метод оптимизации: нулевого порядка (покоординатный
перебор)
k
x
0
V
cos cos d
xн , xк ,Vн ,Vк , н , к
Варьируемые параметры:
Перебор варьируемых параметров направлен:
1.
На устранение невязки на правом конце
траектории
2.
На максимизацию функционала.
Такая задача может быть решена с использованием известного
аппарата динамики полета как задача на максимальную
дальность планирования:
Lпл. макс HK макс
мин
1
К макс
2000
0
0
57,1862
457,6454
1544,6506
3526,4805
5930,7373
8070,9697
9364,627
9893,1826
9999,2695
Функционал:
4000
Xg,м
На данном графике (от 0 до 7) означают варианты
опорных траекторий при варьировании вторых
производных скорости

8.

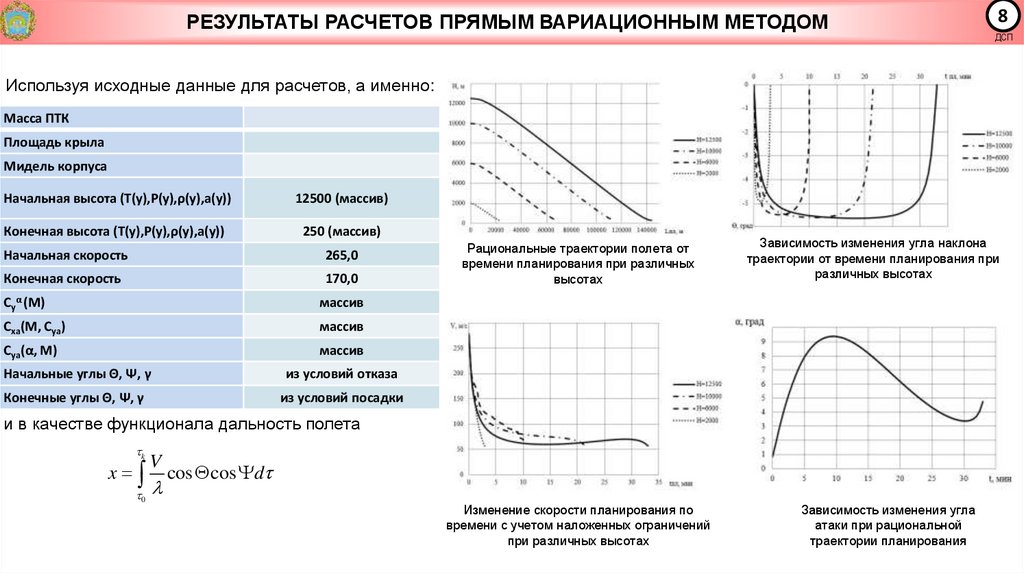
РЕЗУЛЬТАТЫ РАСЧЕТОВ ПРЯМЫМ ВАРИАЦИОННЫМ МЕТОДОМ
8
ДСП
Используя исходные данные для расчетов, а именно:
Масса ПТК
Площадь крыла
Мидель корпуса
Начальная высота (Т(у),Р(у),ρ(у),а(у))
12500 (массив)
Конечная высота (Т(у),Р(у),ρ(у),а(у))
250 (массив)
Начальная скорость
265,0
Конечная скорость
170,0
Суα (М)
массив
Сха(М, Суа)
массив
Суа(α, М)
массив
Начальные углы Θ, Ψ, γ
из условий отказа
Конечные углы Θ, Ψ, γ
из условий посадки
Рациональные траектории полета от
времени планирования при различных
высотах
Зависимость изменения угла наклона
траектории от времени планирования при
различных высотах
и в качестве функционала дальность полета
k
x
0
V
cos cos d
Изменение скорости планирования по
времени с учетом наложенных ограничений
при различных высотах
Зависимость изменения угла
атаки при рациональной
траектории планирования

9.

ВЫВОДЫ
9
ДСП
1.Проведен анализ требований при разработке рекомендаций
летчику по действиям при отказе силовой установки
2.Разработан алгоритм захода на посадку летательного аппарата по
функционалу дальности при выполнении ограничений на конце
траектории (скорость планирования на конце траектории равна
посадочной скорости)
3.Разработана
подпрограмма
определения
рациональных
параметров траекторий движения летательного аппарата при отказе
силовой установки для реализации системы интеллектуальной
поддержки летчика

10.

Краснодарское высшее военное авиационное училище летчиков
Доклад закончен!
г. Краснодар – 2025 г.