Similar presentations:
Комбинаторика
1. Определение
Комбинаторикой называется разделматематики, в котором исследуется,
сколько различных комбинаций
(всевозможных объединений элементов),
подчиненных тем или иным условиям,
можно составить из элементов,
принадлежащих данному множеству.
2. ПЕРЕСТАНОВКИ
Определение.Pn 1 2 3 ..... n 2 n 1 n
Pn n!
Перестановками из n
элементов называют
соединения, которые
состоят из одних и тех
же n элементов и
отличаются одно от
другого только
порядком их
расположения.
3. пример
В соревнованиях участвовало четырекоманды. Сколько вариантов
распределения мест между ними
возможно?
Р4 4! 1 2 3 4 24
4. Вычислите:
Р6 Р5?
5!
Р6 Р5 6! 5! 5! 6 5!
5!
5!
5!
5! 6 1
5
5!
5. Вычислите:
Р20?
Р4 Р16
Р20
20! 16! 17 18 19 20
Р4 Р16 4! 16!
16! 1 2 3 4
17 3 19 5
51 95
1
6. Вычислите:
Рх?
Рх 2 Р2
Рх
х!
Рх 2 Р2 х 2 ! 2!
х 2 ! х 1 х х 1 х
х 2 ! 1 2
2
7. РАЗМЕЩЕНИЯ
8. Вычислить:
А ?3
10
10!
7! 8 9 10
А
720
10 3 !
7!
3
10
9. Вычислить:
А ?5
12
12!
А
12 5 !
7! 8 9 10 11 12
720 132
7!
5
12
10. Вычислить:
А ?4
6
6!
2! 3 4 5 6
А
360
6 4 !
2!
4
6
11. Вычислить:
А ?2
25
25!
23! 24 25
А
25 2 !
23!
24 25 600
2
25
12. Вычислить:
А А3
А8
5
8
4
8
8!
8!
3
!
4
5
6
7
8
4
!
5
6
7
8
8 5 ! 8 4 !
3
!
4
!
8!
5! 6 7 8
8 3 !
5!
5 6 7 8 4 1
5 3 15
6 7 8
13. Вычислить:
А ?5
13
14. пример
Сколько существует вариантовраспределения трех призовых мест, если в
розыгрыше участвуют 7 команд?
7!
4! 5 6 7
А
210
7 3 !
4!
3
7
15. пример
Сколько вариантов распределения трехпутевок в санатории различного профиля
можно составить для пяти претендентов?
5!
2!3 4 5
А
60
5 3 !
2!
3
5
16. самостоятельно
Сколько вариантов расписания можносоставить на один день, если всего
имеется 8 учебных предметов, а в
расписание на день могут быть включены
только три из них?
Сколько различных четырехзначных чисел
можно составить из цифр 0, 1, 2, 3, 4, 5, 6, 7,
8, 9?
17. СОЧЕТАНИЯ
Определение. Сочетаниями из m элементовпо n в каждом n m называются соединения,
каждое из которых содержит n элементов,
взятых из данных m различных элементов, и
которые отличаются одно от другого по крайней
мере одним элементом.
m!
С
m n ! n!
n
m
18. СВОЙСТВА СОЧЕТАНИЙ
19.
Правило суммыПравило произведения
Если надо выбрать n
вещей, причем одну
из них можно выбрать
m способами, а
вторую k способами,
то «или одну или
другую» вещь можно
выбрать m+k
способами
Если надо
выбрать n
вещей, причем
одну из них
можно выбрать
m способами, а
вторую k
способами, то «и
одну и другую»
вещь можно
выбрать m×k
способами
20. Вычислить
38
C
8!
5! 6 7 8
C
8 3 ! 3! 5! 1 2 3
7 8 56
3
8
21. Вычислить
810
C
10!
8! 9 10
C
10 8 ! 8! 8! 1 2
9 5 45
8
10
22. Вычислить
2100
C
100!
98! 99 100
C
100 2 ! 2! 98! 1 2
99 50 4950
2
100
23. Вычислить
C С2
27
2
26
27!
26!
C С
27 2 ! 2! 26 2 ! 2!
25! 26 27 24! 25 26
25! 1 2
24! 1 2
13 27 25 13 13 27 25
13 2 26
2
27
2
26
24. Вычислить
C С5
11
6
11
11!
11!
C С
11 5 ! 5! 11 6 ! 6!
6! 7 8 9 10 11 6! 7 8 9 10 11
6! 1 2 3 4 5
1 2 3 4 5 6!
7 3 2 11 7 3 2 11 2 42 11
84 11 924
5
11
6
11
25. Вычислить
C С С2
5
Вычислить
2
7
2
9
C С С
2
5
2
7
2
9
5!
7!
9!
5 2 ! 2! 7 2 ! 2! 9 2 ! 2!
3! 4 5 5! 6 7 7! 8 9
3! 1 2 1 2 5! 7! 1 2
2 5 7 3 4 9 10 21 36 67
26. Пример: Сколькими способами можно выбрать 3 дежурных, если в классе 30 учащихся?
30!27! 28 29 30
С
30 3 ! 3! 27! 1 2 3
14 29 10 4060
3
30
27. Пример: Сколькими способами можно выбрать двух человек в президиум, если на собрании присутствует 78 человек?
78!76! 77 78
С
78 2 ! 2! 76! 1 2
77 39 3003
2
78
28. Самостоятельно
Сколькими способами можно заполнить лотерейный билет «5 из 36»?
Ответ: 376992
Сколькими способами можно составить
дозор из 3 солдат и одного офицера, если
имеется 80 солдат и 3 офицера?
С С 246480
3
80
1
3
29.
Найдите х, если известно, что СРешение :
2
х 2
21
х 2 !
х 4 ! х 3 х 2
С
х 2 2 ! 2!
х 4 ! 1 2
х 3 х 2
21
2
х 2
2
х 3 х 2 42
х 5 х 36 0
2
30.
Найдите х, если С 1532
х
х1 17; х2 18
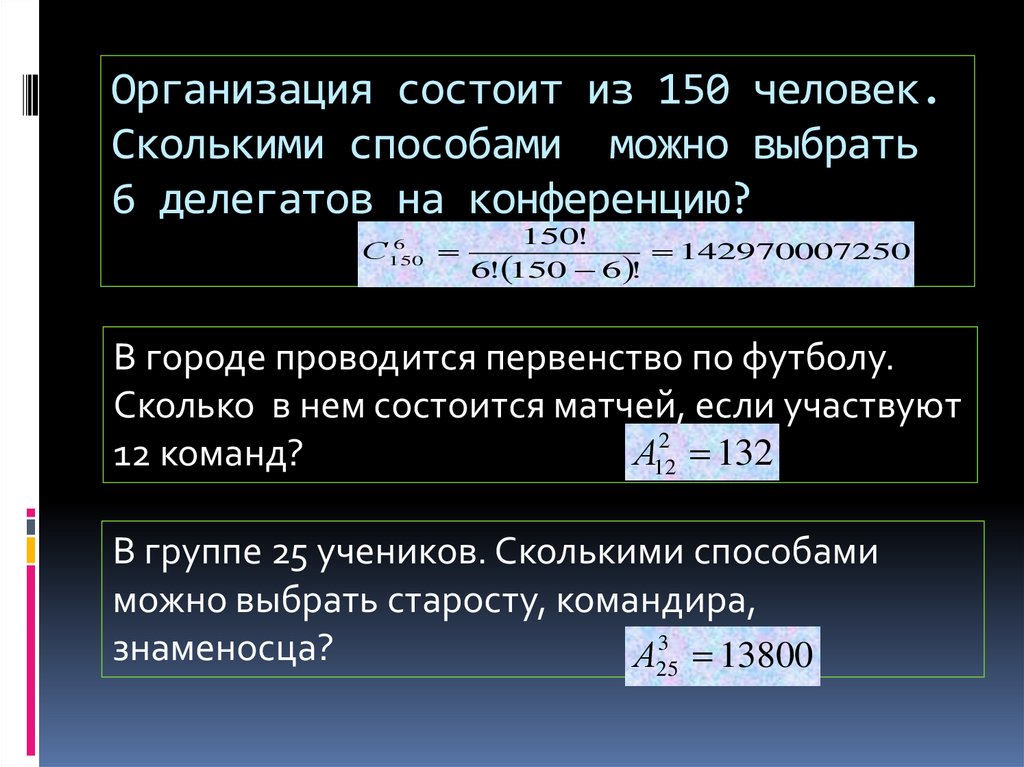
31. Организация состоит из 150 человек. Сколькими способами можно выбрать 6 делегатов на конференцию?
6С150
150!
142970007250
6! 150 6 !
В городе проводится первенство по футболу.
Сколько в нем состоится матчей, если участвуют
А122 132
12 команд?
В группе 25 учеников. Сколькими способами
можно выбрать старосту, командира,
3
знаменосца?
А25
13800
32. Итог
В случае перестановок берутся все элементы иизменяется только их местоположение;
В случае размещений берется только часть
элементов и важно расположение элементов
друг относительно друга;
В случае сочетаний берется только часть
элементов и не имеет значения расположение
элементов друг относительно друга;
Перестановки, размещения и сочетания связаны
формулой
m
n
A
С
P
m
n
33. В тренировках участвовали 12 баскетболистов. Сколько различных стартовых пятерок может образовать тренер?
5С12
792
Сколько различных пятизначных чисел можно
составить из цифр 1, 2, 3, 4, 5 при условии, что ни
одна цифра в числе не повторяется?
Р5 5! 120
В кружке юных математиков 25 членов.
Сколькими способами можно выбрать
председателя кружка, заместителя, редактора
4
А25
303600
стенгазеты и секретаря?
34. Виды случайных событий
Случайное событие – это событие, котороеможет произойти или не произойти.
Если нас интересует какое-либо
определенное событие из всех возможных, то
будем называть его искомым событием.
События называются несовместными, если
никакие два из них не могут произойти в
данном опыте вместе. В противном случае
события называются совместными.
35. Виды случайных событий
События называется достоверным (U),если оно происходит в данном опыте
обязательно.
События называется невозможным (V),
если оно в данном опыте не может
произойти.
36. Виды случайных событий
Полной системой событий А1, А2, ... Аnназывается совокупность всех несовместных
событий, наступление хотя бы одного из
которых обязательно при данном испытании.
Если полная система состоит из двух
несовместных событий, то такие события
называются противоположными и
обозначаются А и Ā.
37. Классическое определение вероятности события
Число, являющееся выражением мерыобъективной возможности наступления
события, называется вероятностью этого
события и обозначается символом Р(А).
Вероятность события А равна отношению
числа m исходов испытания,
благоприятствующих наступлению события
А, к общему числу n всех равновозможных
несовместных исходов, т.е.
m
Р( А)
n
38. Свойства вероятности события
Вероятность любого события естьнеотрицательное число, не
превосходящее единицу.
Вероятность достоверного события
равна единице.
Вероятность невозможного
события равна нулю.
39. Зная вероятность события А, можем найти и вероятность противоположного ему события Ā: Р(Ā)=1-Р(А)
Бросают игральную кость. Найти вероятностьтого, что выпадет любое число очков, кроме 5.
Решение: Число всех возможных исходов: 6.
Поэтому вероятность того, что выпадет 5
(событие А):
.
1
Р( А)
6
Вероятность того, что выпадет
любое число
очков, кроме 5 (событие Ā):
Р( А ) 1 Р( А) 1
1
5
40.
Даны 5 точек, никакие три из которых нележат на одной прямой. Найти
вероятность того, что, выбрав наугад две
точки, учащийся получит нужную прямую.
Решение: Пусть событие А – выбор
исходной прямой. Число всех возможных
исходов равно количеству прямых. Так как
прямая определяется парой точек и
порядок точек не имеет значения, то
5!
3! 4 5
n C
10
5 2 ! 2! 3! 1 2
1
Р( А)
10
2
5
41.
Буквы а, а, в, к, к, о, х написаны на отдельныхкарточках. Какова вероятность того, что
извлекая все эти карточки по одной наудачу,
мы получим в порядке их выхода слово
«Каховка»?
Решение: Событие А – слово «Каховка».
Буквы «а» и «к» встречаются дважды, и если
мы их поменяем местами, то получим это же
слово. => благоприятных исходов m=4.
Всего равновозможных исходов – число
перестановок из 7 элементов n=Р!=7!=5040.
m
4
1
Р ( А)
n 5040 1260
42.
Набирая номер телефона, абонент забылодну последнюю цифру и набрал ее
наудачу. Найдите вероятность того, что
набрана нужная цифра.
Решение: пусть В – событие, состоящее в
том, что набрана нужная цифра (m=1).
Диск телефонного аппарата содержит 10
цифр (n=10).
m 1
Р( В)
0,1
n 10
43.
Набирая номер телефона, абонент забылдве последнии цифры и набрал их наудачу.
Найдите вероятность того, что набраны
нужные цифры.
Решение: пусть В – событие, состоящее в
том, что набраны нужные цифры.
Благоприятствует событию В только один
случай.
10!
8! 9 10
n А
90
10 2 !
8!
2
10
m 1
Р( В)
n 90
44.
Известно, что 5% всех мужчин и 0,25% всехженщин – дальтоники. Наудачу выбранное
лицо страдает дальтонизмом. Какова
вероятность того, что это лицо – мужчина
(считать, что мужчин и женщин одинаковое
число).
Решение: Из 10000 мужчин 10000×0,05=500
страдающих дальтонизмом, а женщин
10000×0,0025=25. таким образом из 20000
человек 525 страдает дальтонизмом.
m 500 20
Р
n 525 21
45.
В партии из 100 деталей имеется 5 бракованных.Определите вероятность того, что взятая
наудачу деталь окажется стандартной.
Выбирают наугад число от 1 до 100. определите
вероятность того, что в этом числе не окажется
цифра 3.
Найдите вероятность того, что наугад
выбранное число от 1 до 60 делится на 60.
В классе 17 девочек и 14 мальчиков. Определить
вероятность того, что оба вызванных ученика
окажутся а) мальчиками; б) девочками.
0,95; 0,81; 1/60; 91/465; 136/465.
46. Вопросы к зачёту
1. Что такое комбинаторика?2. В чём состоит правило суммы?
3. В чём состоит правило
произведения?
4. Что такое факториал?
5. Что такое перестановки?
6. Запишите формулу для нахождения
числа перестановок.
7. Что такое размещения?
47. Вопросы к зачёту
8. Запиши формулу для нахождениячисла размещений.
9. Что такое сочетание?
10. Запишите формулу для нахождения
числа сочетаний.
11. Объясните принцип построения
треугольника Паскаля.
12. Запишите формулу, связывающую
перестановки, сочетания и
размещения.
48. Вопросы к зачёту
13. В чём различие междуперестановками, размещениями,
сочетаниями?
14. Что такое событие? Какие виды
событий вы знаете?
15. Что такое исход? Дайте
определение.
16. Какие виды исходов вы знаете?
Приведите примеры.
49. Вопросы к зачёту
16. \о Какие виды исходов вы знаете?Приведите примеры.
17. Дайте классическое определение
вероятности.





























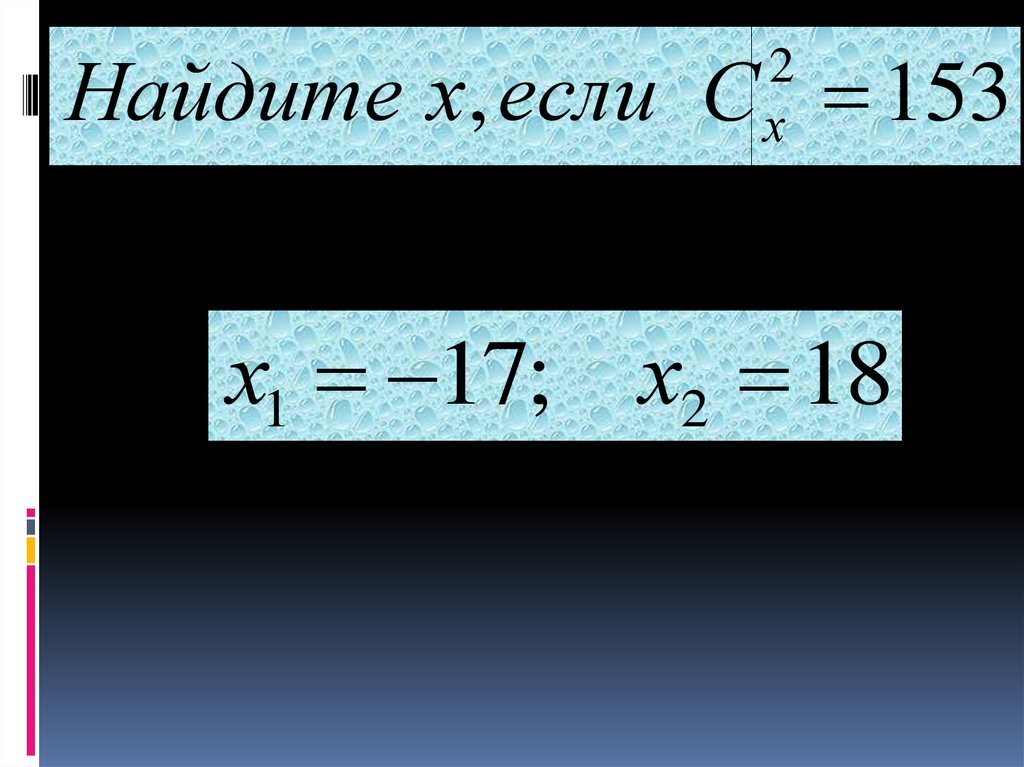


















 mathematics
mathematics








