Перпендикуляр и наклонные. Угол между прямой и плоскостью

1.

2.

Цель урока:
Повторить основные понятия: перпендикуляр,
наклонная, проекция.
Вспомнить теорему о трех перпендикулярах и
такое важное понятие, как угол между прямой и
плоскостью.
Решить несколько задач на перпендикуляр и
наклонные.

3.

НАПОМНИМ ОСНОВНЫЕ ПОНЯТИЯ
Отрезок АН –
перпендикуляр,
проведенный из точки А к
плоскости α. Точка Н –
основание перпендикуляра.
Отрезок АМ –
наклонная, М – основание
наклонной.
Отрезок МН называется
проекцией
наклонной АМ на плоскость
α.

4.

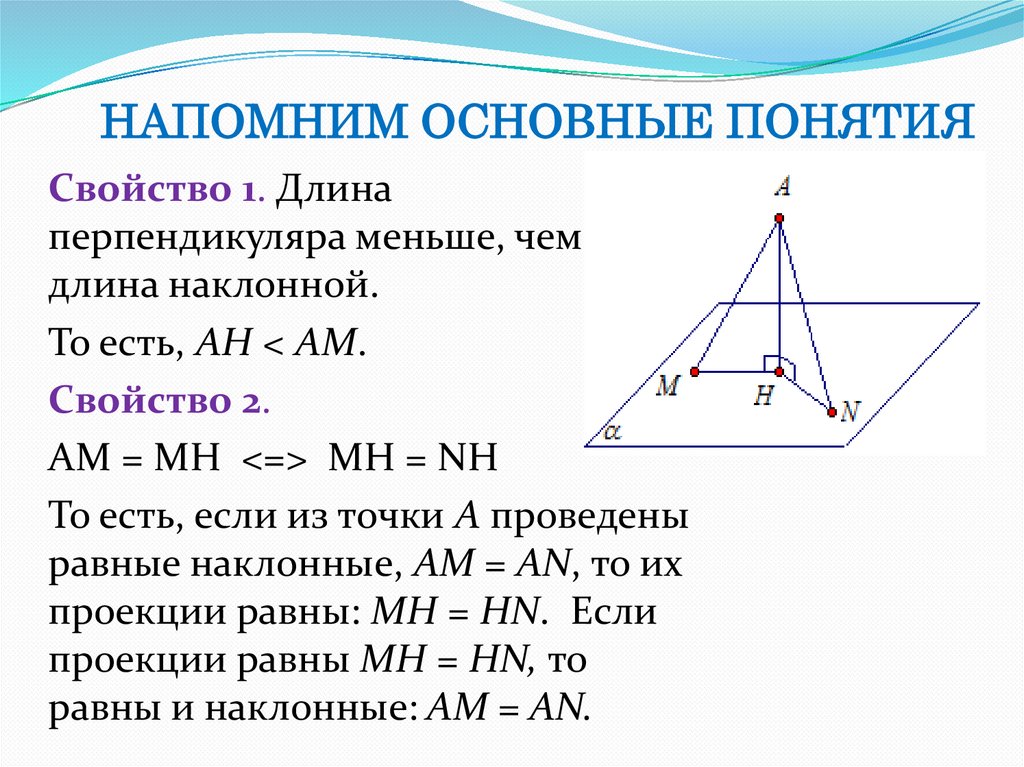
НАПОМНИМ ОСНОВНЫЕ ПОНЯТИЯ
Свойство 1. Длина
перпендикуляра меньше, чем
длина наклонной.
То есть, АН < AM.
Свойство 2.
AM = MH <=> MH = NH
То есть, если из точки А проведены
равные наклонные, АМ = AN, то их
проекции равны: MH = HN. Если
проекции равны MH = HN, то
равны и наклонные: АМ = AN.

5.

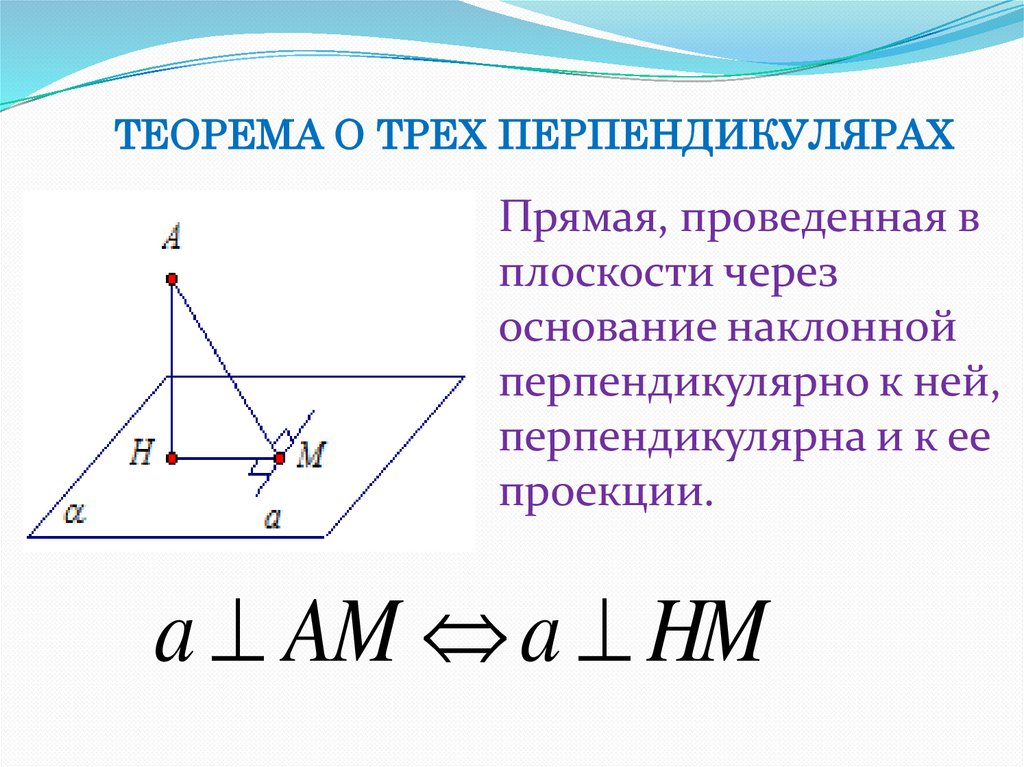
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
Прямая, проведенная в
плоскости через
основание наклонной
перпендикулярно к ней,
перпендикулярна и к ее
проекции.
a AM a HM

6.

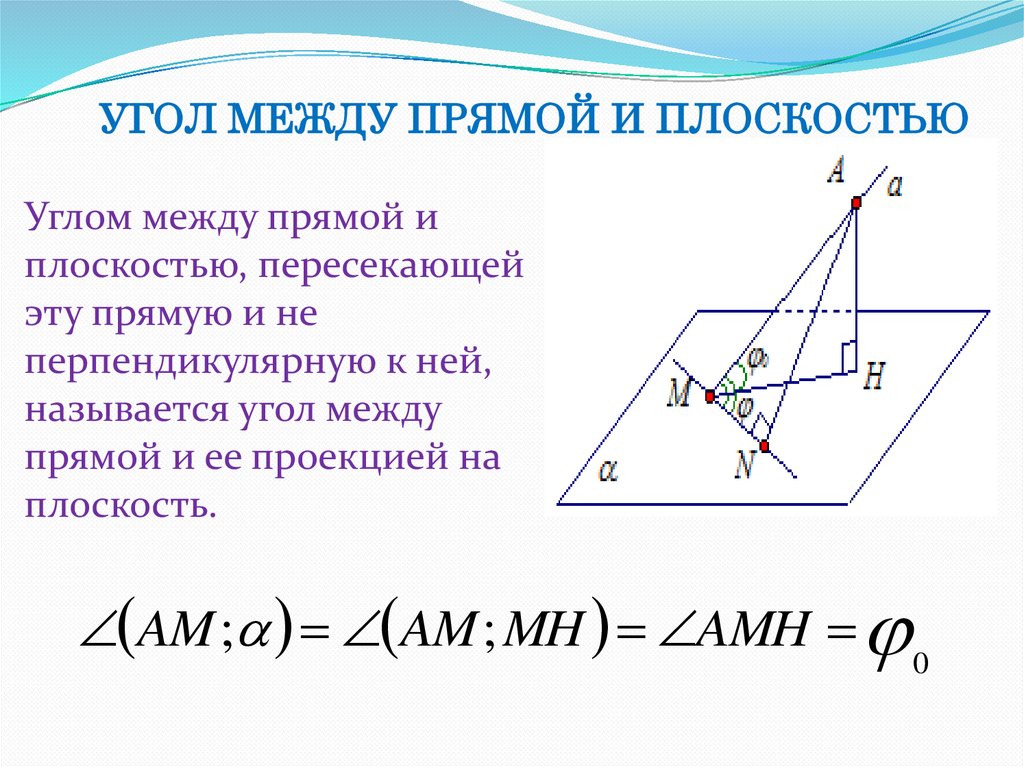
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между прямой и
плоскостью, пересекающей
эту прямую и не
перпендикулярную к ней,
называется угол между
прямой и ее проекцией на
плоскость.
AM ; AM ; MH AMH
0

7.

РЕШЕНИЕ ЗАДАЧ
№1
Прямая ОМ перпендикулярна плоскости
треугольника АВС и проходит через центр О вписанной в него
окружности.
Докажите, что точка М равноудалена:
от прямых АВ, ВС, СА.
от всех точек вписанной окружности и от всех касательных
к ней.
Найдите это расстояние, если известны радиус r окружности
и длина ОМ = h.
Докажите равенство углов наклона прямых МТ (где Т –
любая точка окружности) к плоскости АВС.
Найдите тангенс этих углов.

8.

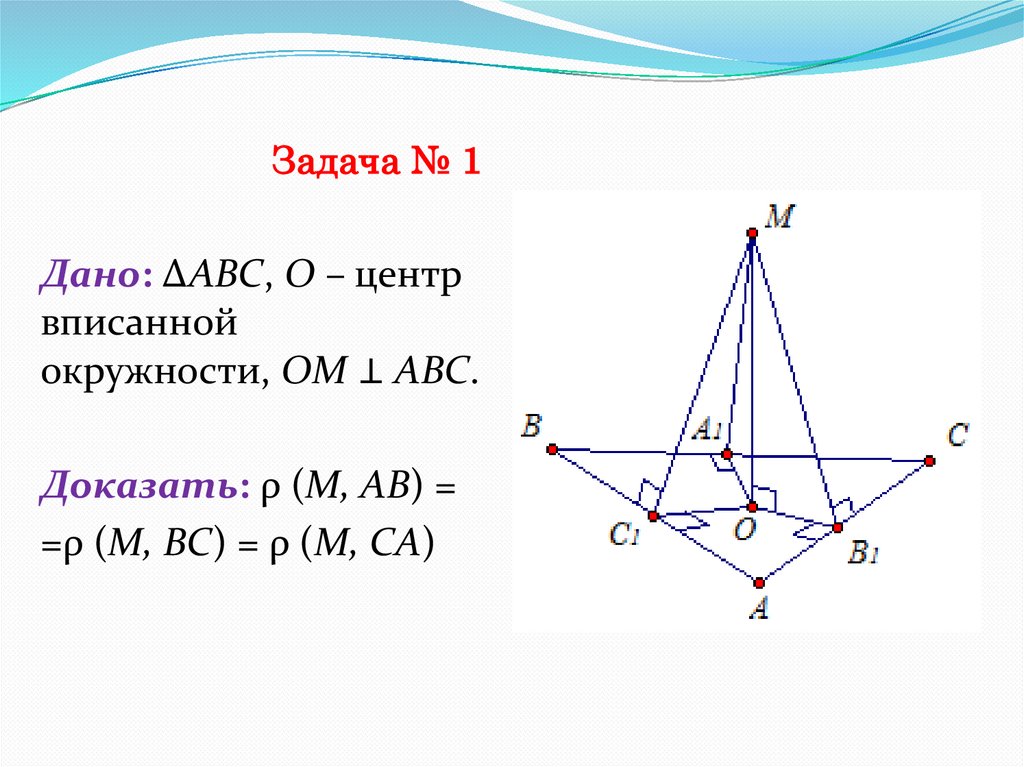
Задача № 1
Дано: ∆АВС, О – центр
вписанной
окружности, ОМ ⊥ АВС.
Доказать: ρ (М, АВ) =
=ρ (М, ВС) = ρ (М, СА)

9.

Задача № 1.1
Пусть А1 ; В1 ; С1 – это точки касания окружности
к сторонам треугольника. ОС1 ; ОА1 ; ОВ1 –
радиусы этой окружности. Тогда, по
свойству, ОС1 ⊥ АВ, ОА1 ⊥ ВС, ОВ1 ⊥ АС.
МО – перпендикуляр к плоскости АВС. ОС1 –
проекция наклонной МС1 на плоскость АВС. Так
как ОС1 ⊥ АВ, то МС1 ⊥ АВ (по теореме о трех
перпендикулярах). Значит, МС1 – это расстояние
от точи М до прямой АВ, МС1 = ρ (М, АВ).
Аналогично получаем, что МА1 = ρ (М, ВС), МВ1 =
ρ (М, СА).
Треугольники МОС1 ; МОА1 ; МОВ1 равны по
двум катетам (катеты ОС1 ; ОА1 ; ОВ1 равны как
радиусы вписанной окружности, катет ОМ –
общий). Из равенства треугольников следует,
что МС1 = МА1 = МВ1. А значит, ρ (М, АВ) = ρ (М,
ВС) = ρ (М, СА), что и требовалось доказать.

10.

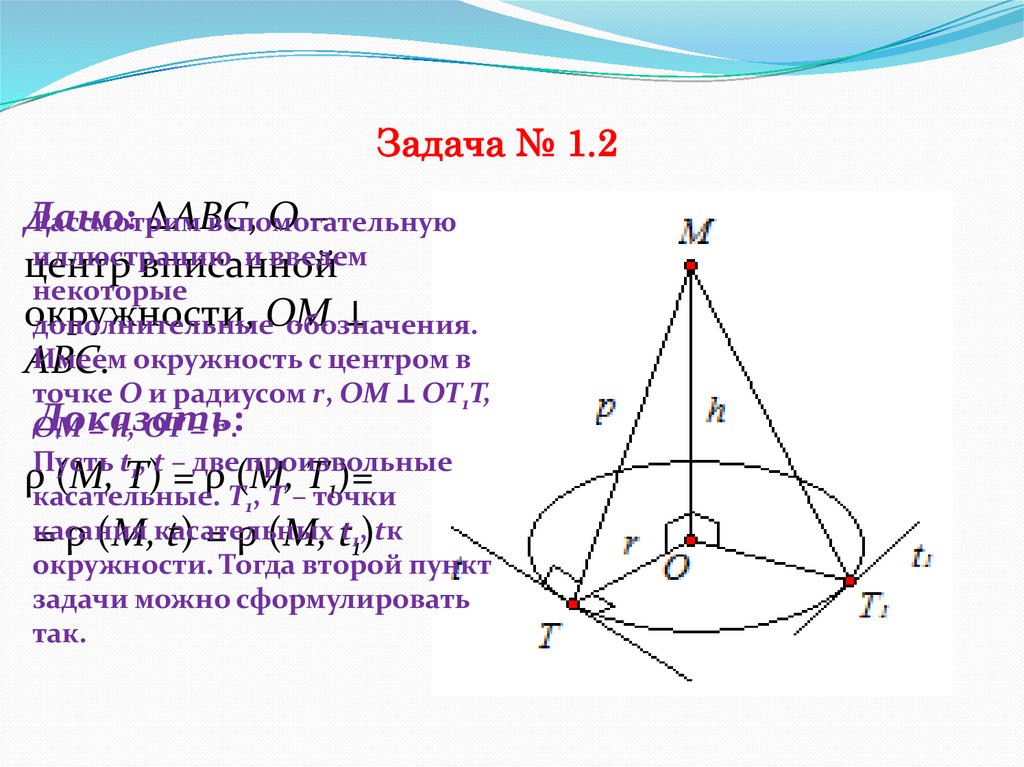
Задача № 1.2
Дано:
∆АВС,
О–
Рассмотрим
вспомогательную
иллюстрацию
и введем
центр
вписанной
некоторые
окружности,
⊥
дополнительныеОМ
обозначения.
Имеем окружность с центром в
АВС.
точке О и радиусом r, ОМ ⊥ ОТ1Т,
Доказать:
ОМ
= h, OT = r .
t1, t – две произвольные
ρПусть
(М,
Т) = ρ (М, Т1)=
касательные. Т1, Т – точки
касания
= ρ (М,касательных
t) = ρ (М, tt11,)tк
окружности. Тогда второй пункт
задачи можно сформулировать
так.

11.

Задача № 1.2
Касательные t1 ; t касаются окружности в
точках Т, Т1 соответственно. Радиус,
проведенный в точку касания касательной,
перпендикулярен касательной. То есть ОТ ⊥ t.
ρ (М, Т) = МТ, ρ (М, Т1) = МТ1
ОТ – это проекция наклонной МТ на плоскость
окружности. Прямая t лежит в этой плоскости.
Так как ОТ ⊥ t, то МТ ⊥ tпо теореме о трех
перпендикулярах. Значит, ρ (М, t) = МТ.
Аналогично, ρ (М, t1) = МТ1.
Рассмотрим прямоугольные
треугольники МОТ и МОТ1. Катет ОМ –
общий, ОТ = ОТ1 как радиусы. Значит,
треугольники МОТ и МОТ1 равны по двум
катетам. Следовательно, МТ = МТ1, а значит, ρ
(М, t) = ρ (М, t1), ρ (М, Т) = ρ (М, Т1), что и
требовалось доказать.

12.

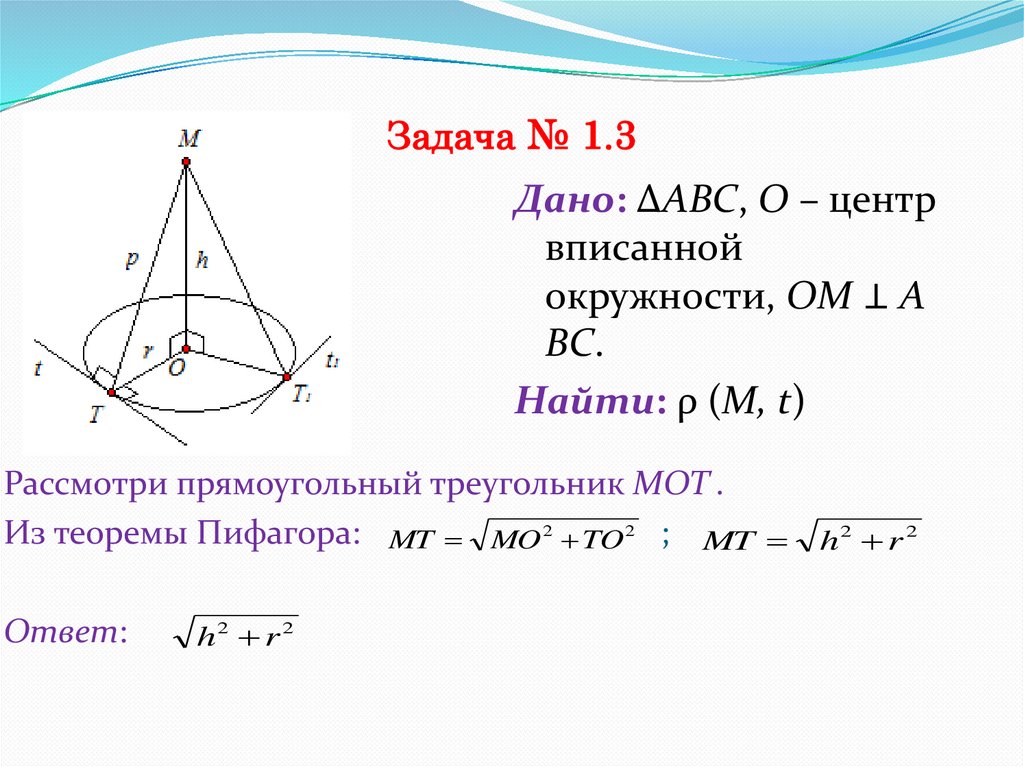
Задача № 1.3
Дано: ∆АВС, О – центр
вписанной
окружности, ОМ ⊥ А
ВС.
Найти: ρ (М, t)
Рассмотри прямоугольный треугольник МОТ .
Из теоремы Пифагора: MT MO 2 TO2 ; MT h2 r 2
Ответ:
h2 r 2

13.

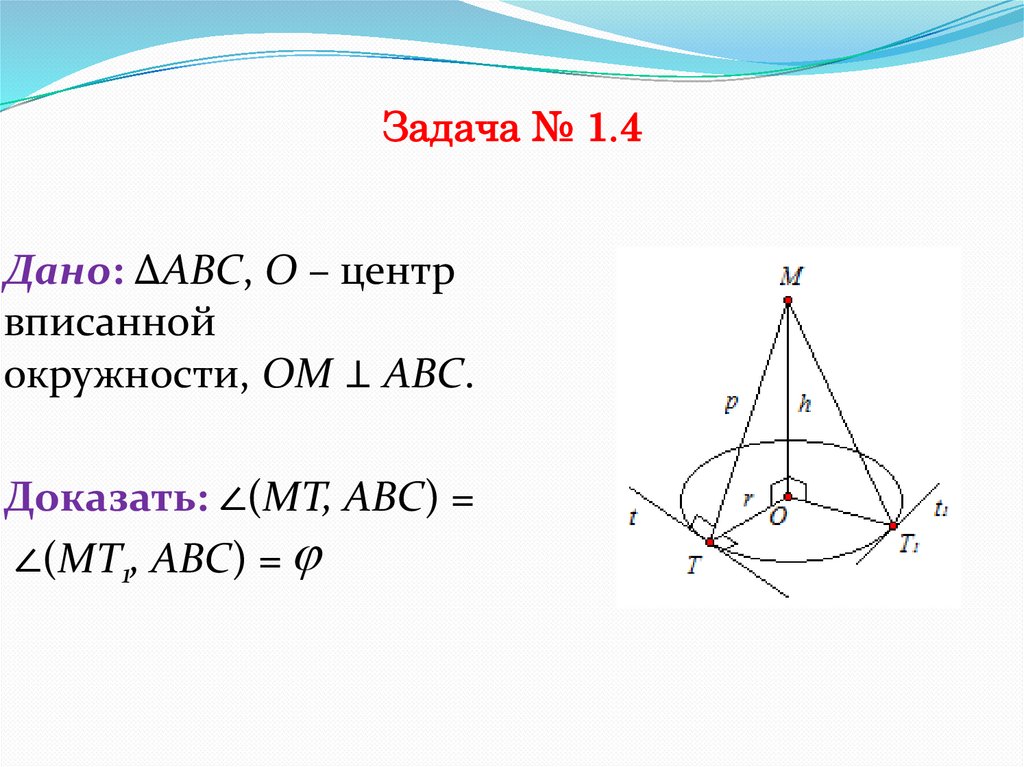
Задача № 1.4
Дано: ∆АВС, О – центр
вписанной
окружности, ОМ ⊥ АВС.
Доказать: ∠(МТ, АВС) =
∠(МТ1, АВС) =

14.

Задача № 1.4
ОТ – проекция наклонной МТ на
плоскость ABC.
Значит, ∠(МТ, АВС) = ∠(МТ, ОТ) = ∠МТО.
Аналогично, ∠(МТ1, АВС) = ∠(МТ1, ОТ1) =
∠МТ1О.
Мы доказали, что
треугольники МОТ и МОТ1 равны, а
значит, и углы МТО и МТ1Оравны.
Обозначим, их величину за φ. Тогда,
∠(МТ, АВС) = ∠(МТ1, АВС) = φ, что и
требовалось доказать.

15.

Задача № 1.5
Дано: ∆АВС, О – центр
вписанной
окружности, ОМ ⊥ АВС.
Найти: tg φ.
Рассмотри прямоугольный треугольник МОТ.
MO
h
tg tg MTO
OT
r