Электронно-цифровая подпись

1. Электронно-цифовая подпись

2. Таксономия ЭЦП

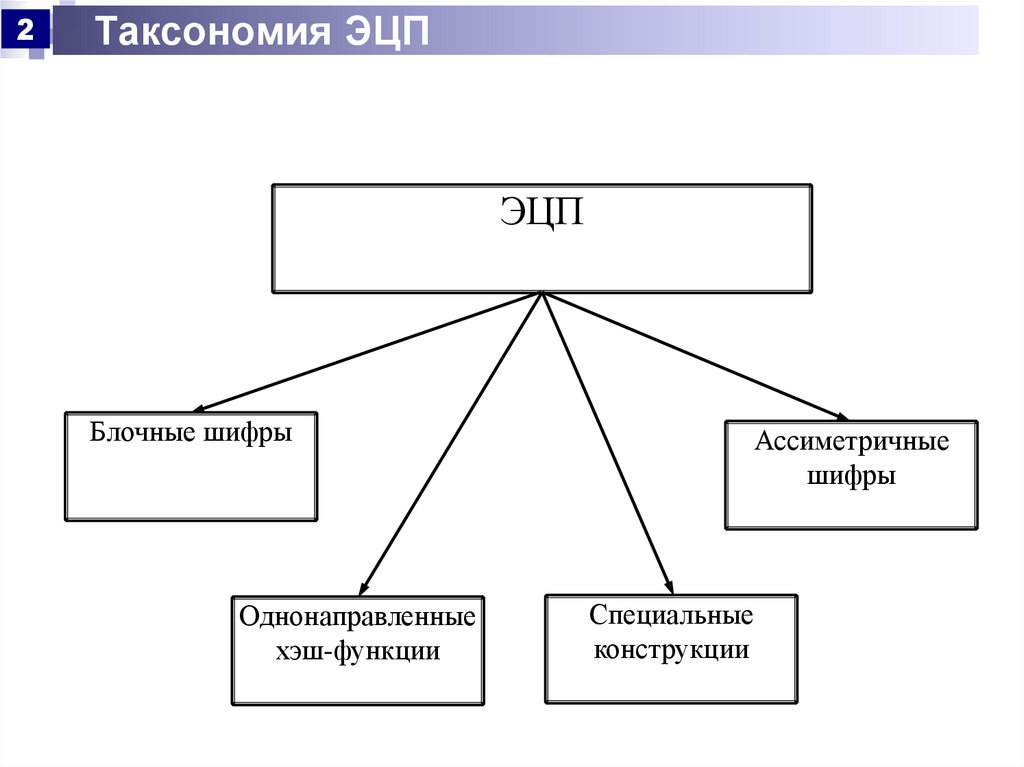
2
Таксономия ЭЦП
ЭЦП
Блочные шифры
Однонаправленные
хэш-функции
Ассиметричные
шифры
Специальные
конструкции

3. ЭЦП на основе ассиметричных алгоритмов

3
ЭЦП на основе ассиметричных алгоритмов
RSA
(d, n) – параметры, с мощью которых
формируется подпись: S = h(M)d(mod n)
(n, e) – параметры проверки подписи:
h(M) = Se(mod n).
Эль-Гамаль
x – закрытый ключ, k –случайный параметр:
r = gk mod p; s = (h(M)-xr)k-1 (mod p-1)
(r, s) – подпись
(p,g,y) – открытый ключ
yrrs = gh(M) (mod p)

4. Проверка корректности Эль-Гамаля

4
Проверка корректности Эль-Гамаля
Исходя из того, что
m= xr + sk (mod p-1)
По малой т. Ферма
gm = gxr gks = (gx)r (gk)s = (y)r (r)s
(mod p)

5. ГОСТ 34.10-2018 (Формирование ЭЦП)

5
ГОСТ 34.10-2018 (Формирование ЭЦП)
Дана ЭК и ее параметры и точка на ней P.
Ключ шифрования d – целое число, 0 < d < q
Ключ расшифрования Q = (xQ, yQ), Q = d*P
Вычислить h = H(M), где h представляется в виде
целого числа – z;
Вычисляется e = z mod q, выбираем 0 < k < q
Вычисляется С = k*P и r = xc mod q, где xc –
координата х (≠0) точки С.
Вычиcляется s = (rd+ke) mod q. Проверяется s≠0.
Цифровая подпись S=(r*|s*), r*, s* - вектора
соответствующие r и s.

6. ГОСТ 34.10-2018 (Проверка ЭЦП)

6
ГОСТ 34.10-2018 (Проверка ЭЦП)
По вектора r* и s* вычислить значения r и s, и
проверить условие для каждого <q;
Вычислитьяется h = H(M), где далее h
представляется в виде целого числа – z;
Вычисляется e = z mod q
Вычисляется v = e-1 mod q
Вычисляется z1 = sv mod q и z2 = -rv mod q
Вычисляется точка ЭК C = z1P + z2Q. Находится
R = xc mod q, xc – координата точки C.
Если R = r, то ЭЦП истинная.

7. DSA

7
DSA
Секретный ключ – число 0 < x < q ;
Открытый ключ – y = gx (mod p), где g = n(p-1)/q mod p
Формирование подписи
Выбирается 0<k<q
Вычисляется r = (gk mod p) mod q. Проверка r.
Вычисляется s = k-1(H(M) + xr) mod q. Проверка s.
Подпись (r, s).
Проверка подписи
Вычисляется w = s-1 mod q
Вычисляется u1 = H(M) w mod q и u2 = r w mod q
Вычисляется v = (gu1 yu2 mod p) mod q
Если v = r, то подпись верна.

8.

8